Supplementary Dataset Generated by Hadley & Imamura Collaboration

Introduction

Using numerical hydrodynamic techniques, the Hadley & Imamura collaboration — see especially Paper I and Paper II — has studied the dynamical development of nonaxisymmetric instabilities in toroidal configurations that have a range of "star-to-disk" mass ratios and a wide variety of (initially axisymmetric) geometric structures. We have begun to analyze the results of these numerical simulations in the context of what is known, analytically, about normal modes of oscillation and nonaxisymmetric instabilities in massless Papaloizou-Pringle tori. On the analytic side, our focus has been on the very informative stability analysis published by Blaes (1985).

This brief appendix is provided primarily to support our accompanying discussion of the "Characteristics of Unstable Eigenvectors in Self-Gravitating Tori;" especially the subsection of that chapter in which some results from the Hadley & Imamura collaboration are directly compared to the analytic analysis by Blaes (1985). In addition to the relatively small number of individual models whose unstable eigenvectors have been described in the published literature — see especially the three papers listed below — Hadley and Imamura have stored digital results from a very large number of model simulations in an online Stardisks repository. We greatly appreciate being granted permission (explicitly by K. Z. Hadley) to access this data repository and to post this link so that other researchers may study the accumulated data as well.

Specifics of Database

The initial, axisymmetric toroidal configuration that is associated with each simulation is uniquely characterized by the following set of physical parameters:

•	<math>~n</math>	…	Polytropic index
•	<math>~q</math>	…	Power-law index characterizing angular velocity profile — but see the relevant note regarding Simple Rotation Profiles, below
•	<math>~M_*/M_\mathrm{disk}</math>	…	Star-to-disk (i.e., star-to-torus) mass ratio
•	<math>~R_-/R_+</math>	…	Ratio of inner-to-outer edge of the torus, in its equatorial plane

In addition to specifying these four parameters, the Hadley & Imamura collaboration also tag each evolution with an integer value of <math>~m</math>, to identify the nonaxisymmetric mode that was observed to be fastest growing. For example, following the "star-disk models" link that appears at the top of the category list on the home page of the Stardisks repository will bring you to a page that provides active links to 32 separate model categories, such as:

	Model Category			To go directly to the identified page …
	<math>~(n, q, m)</math>	<math>~=</math>	<math>~(1.5, 1.0, 1)</math>	click this link
	<math>~(n, q, m)</math>	<math>~=</math>	<math>~(1.5, 1.75, 3)</math>	click this link
Most relevant here ➠	<math>~(n, q, m)</math>	<math>~=</math>	<math>~(1.5, 2.0, 2)</math>	click this link
	<math>~(n, q, m)</math>	<math>~=</math>	<math>~(2.5, 1.5, 2)</math>	click this link

Clicking on any one of these category links will take you to a page containing a number of separate tables — each labeled with the relevant <math>~M_*/M_\mathrm{disk}</math> value — and, within each table, a (sometimes large!) number of rows, each characterized (usually in the 2^nd column) by the specific model's <math>~R_-/R_+</math>.

For example, on the page associated with the model category that we have identified (see red arrow, above) as most relevant to our accompanying discussions, we find that the 2nd row of the top-most table details various properties of a particular model evolution uniquely identified by the set of parameters, <math>~(n, q, M_*/M_\mathrm{disk}, R_-/R_+)</math> = <math>~(1.5, 2.0, 0.0, 0.1008)</math>. And on the same page, the last row of the bottom-most table details various properties of another particular model evolution uniquely identified by the set of parameters, <math>~(n, q, M_*/M_\mathrm{disk}, R_-/R_+)</math> = <math>~(1.5, 2.0, 1000.0, 0.8002)</math>. In both of these model evolutions, the fastest growing unstable mode was <math>~m = 2</math>.

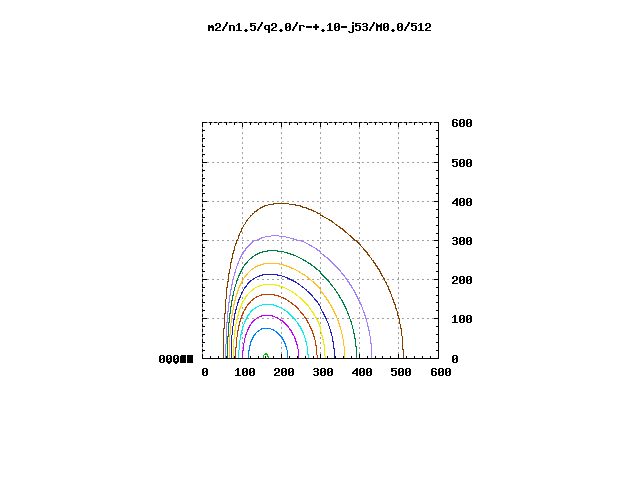
At the very bottom of every <math>~(n,q,m)</math> model category page is a list of — and a hypertext link to — ten "Image Tables." Clicking on the "eqContour" link takes you to a page that contains a thumbnail image showing the meridional-plane density contours of the equilibrium model that served as the initial condition for every evolution catalogued under the chosen <math>~(n,q,m)</math> category. The thumbnail images are laid out on a two-dimensional, rectangular lattice whose horizontal position is set by the specific model's mass ratio and whose vertical position is set by the model's geometric ratio, <math>R_-/R_+</math>.

Figure 1

<math>~(n, q, M_*/M_\mathrm{disk}, R_-/R_+) = ~(1.5, 2.0, 0.0, 0.1008)</math>

Initial Meridional-plane Contours

Radial Profile of Unstable m = 2 Eigenfunction

Phase Locus of Unstable m = 2 Eigenfunction

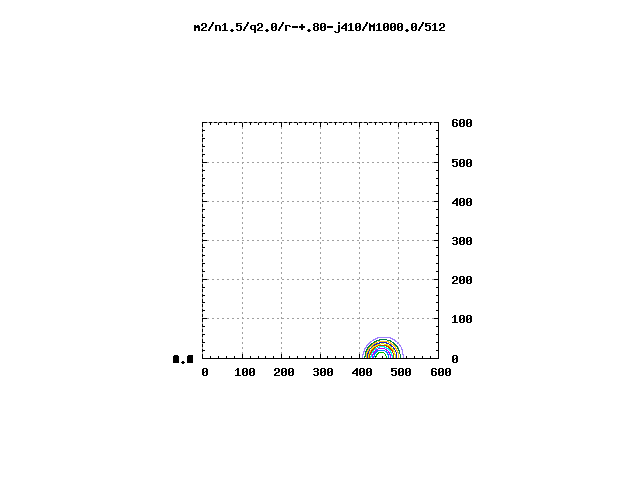
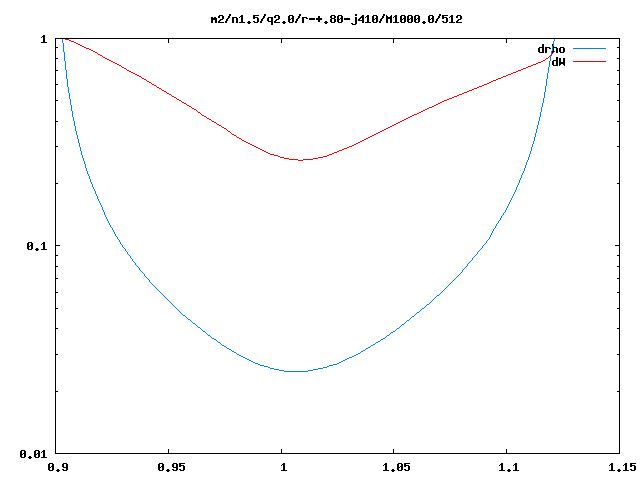
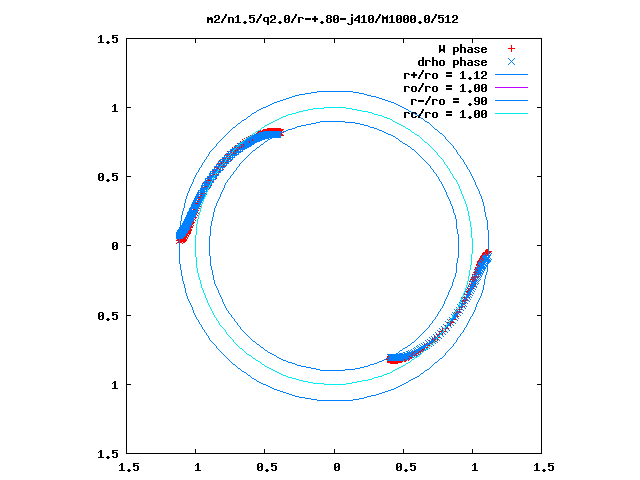
The image displayed here, on the left in Figure 1, was extracted from coordinate position <math>~(M_*/M_\mathrm{disk}, R_-/R_+)</math> = <math>~(0.0,0.1)</math>, near the upper-left corner of the "eqContour" Image Table associated with our above-identified "most relevant" model category, namely, <math>~(n,q,m)</math> = <math>~(1.5,2.0,2)</math>. This is a very thick (toroidal-shaped), isolated self-gravitating disk; that is, there is no central star associated with this dynamical system. The image displayed on the left in Figure 2, was extracted from coordinate position <math>~(M_*/M_\mathrm{disk}, R_-/R_+)</math> = <math>~(1000.0, 0.8)</math>, near the bottom-right corner of the same "eqContour" Image Table. This is a very slender and nearly massless disk/torus; it is orbiting a central (point-like) star whose mass is one thousand times larger than the mass of the disk.

Figure 2

<math>~(n, q, M_*/M_\mathrm{disk}, R_-/R_+) = ~(1.5, 2.0, 1000.0, 0.8002)</math>

Initial Meridional-plane Contours

Radial Profile of Unstable m = 2 Eigenfunction

Phase Locus of Unstable m = 2 Eigenfunction

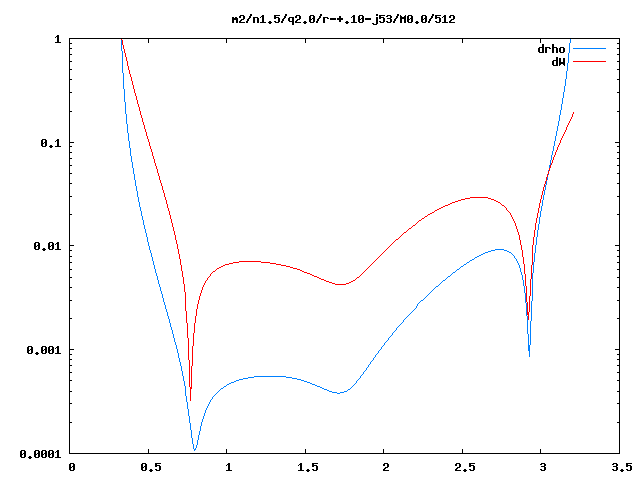
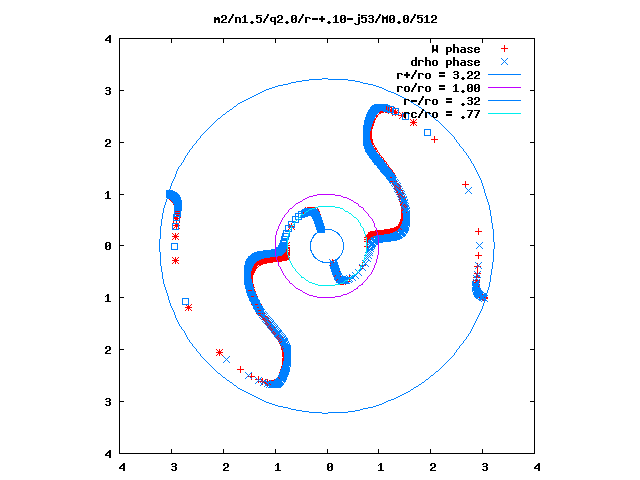
In an analogous fashion, the images displayed here in the middle of Figure 1 and Figure 2 were extracted from the <math>~|\delta\rho|/\rho(\varpi)</math> Image Table associated with the <math>~(n,q,m)</math> = <math>~(1.5,2.0,2)</math> model category. And the images displayed on the right in both figures were extracted from the "<math>~\delta\rho</math> phase(m)" Image Table associated with the <math>~(n,q,m)</math> = <math>~(1.5,2.0,2)</math> model category.

Relationship to Studies of Slender, Massless Tori

In an accompanying chapter, we have discussed the "characteristics of unstable eigenvectors in self-gravitating tori" — such as the ones presented by the Hadley & Imamura collaboration — in the context of analytic studies of normal modes of oscillation in tori that …

have <math>~n = \tfrac{3}{2}</math> — although this can be readily generalized;
have uniform specific angular momentum — that is, have <math>~q = 2.0</math>;
are massless, that is, have <math>~M_*/M_\mathrm{disk} = \infty</math>;
are slender — that is, they have geometric ratios, <math>~R_-/R_+</math> near unity.

As a group, these configurations define a subset of a much larger set of massless tori whose (initial) axisymmetric, equilibrium structures are completely definable in terms of analytic expressions. As has been discussed in an accompanying chapter, the structural and stability properties of these configurations were first brought to the attention of the astrophysics community, in the context of Newtonian systems, by Papaloizou & Pringle (1984, MNRAS, 208, 721-750). Hence, they are frequently referred to as Papaloizou-Pringle tori — or, PP tori, for short.

As we have pointed out, the relative thickness of a PP torus can be expressed in terms of the dimensionless Bernoulli constant, <math>~C_B^'</math> — a physical parameter highlighted by Papaloizou & Pringle (1984) — as follows:

<math> ~\frac{R_{-}}{R_{+}} = \frac{ 1 - \sqrt{1-2C_\mathrm{B}^'} }{1 + \sqrt{1-2C_\mathrm{B}^'} } . </math>

And in our review of Kojima's (1986) work, we showed that the square of the Mach number at the cross-sectional center (subscript "0") of the torus can also be expressed in terms of this dimensionless Bernoulli constant. Specifically,

<math>~\mathfrak{M}_0^2 \equiv \frac{(v_\varphi\|_0)^2}{(c_s\|_0)^2}</math>	<math>~=</math>	<math>~2n [ 1- 2C_B^' ]^{-1}</math>
<math>~\Rightarrow ~~~~ [1 - 2C_B^'] </math>	<math>~=</math>	<math>~\frac{2n}{\mathfrak{M}_0^2} \, . </math>

Now, instead of specifying the system's Mach number in his analytic examination of the stability of PP tori, Blaes (1985) defines the dimensionless order parameter,

<math>~\equiv</math>

<math>~\frac{2n}{\mathfrak{M}_0^2} \, .</math>

Putting these algebraic expressions together, it is clear that in massless PP tori,

or, inverting this expression,

With this information in hand, we expect that results from the stability analysis performed by Blaes (1985) on PP tori having <math>~M_*/M_\mathrm{disk} = \infty</math> and <math>~\beta \ll 1</math> should most appropriately be compared to models from the Hadley & Imamura collaboration that have <math>~M_*/M_\mathrm{disk} \gg 1</math> and <math>~R_-/R_+ \approx 1</math>. Numerical simulation results from the model illustrated, above, in our Figure 1 are not likely to compare well with the analytic stability analysis presented by Blaes because the torus is very thick <math>~(R_-/R_+ = 0.1)</math> and massive <math>~(M_*/M_\mathrm{disk} = 0)</math>. On the other hand, the model illustrated, above, in our Figure 2 presents a likely candidate for comparison, as its parameter values are,

<math>~\frac{M_*}{M_\mathrm{disk}}</math>	<math>~=</math>	<math>~1000 \, ,</math>
and,
<math>~\frac{R_-}{R_+} = 0.8</math>	<math>~\Rightarrow</math>	<math>~\beta \approx 0.11 \, .</math>

Panels B and C of Figure 3 in an accompanying chapter presents this direct comparison.

Simple Rotation Profiles

In support of the broad scope of problems that are discussed within this online Hypertext_Book, a separate chapter provides a brief review of the variety of Simple Rotation Profiles that are typically referenced and/or employed across the research community in discussions of astrophysical fluid flows. The Hadley & Imamura collaboration has explored the stability of initially axisymmetric, toroidal configurations that have a variety of angular velocity profiles. As has been pointed out, above, each of their angular velocity profiles, <math>~\Omega(\varpi)</math>, is uniquely prescribed via the choice of the power-law index, <math>~q</math>, through the expression (see, for example, equation 6 of Paper II),

<math>~\frac{\Omega(\varpi)}{\Omega_0}</math>

<math>~\biggl(\frac{\varpi}{\varpi_0}\biggr)^{-q} \, ,</math>

where the subscript, "0", denotes the location of the density and pressure maximum inside the initial, equilibrium toroidal configuration. All of these fall within the category of Simple Rotation Profiles, in the sense we have reviewed. However, care must be taken when drawing parallels between our review and the discussions presented by the Hadley & Imamura collaboration because our review also refers to a power-law index, <math>~q</math> — for clarity, here, let's call it, <math>~q_\mathrm{H\_Book}</math> — but its definition is different from the one used by the Hadley & Imamura collaboration — for clarity, call it, <math>~q_\mathrm{HI}</math>. In order to relate one set of discussions to the other requires the mapping,

<math>~q_\mathrm{HI}~~~\leftrightarrow~~~(2-q_\mathrm{H\_Book}) \, .</math>

User:Tohline/Appendix/Ramblings/Hadley and Imamura Supplementary Database

Contents

Supplementary Dataset Generated by Hadley & Imamura Collaboration

Introduction

Specifics of Database

Relationship to Studies of Slender, Massless Tori

Simple Rotation Profiles

See Also

Navigation menu

Search