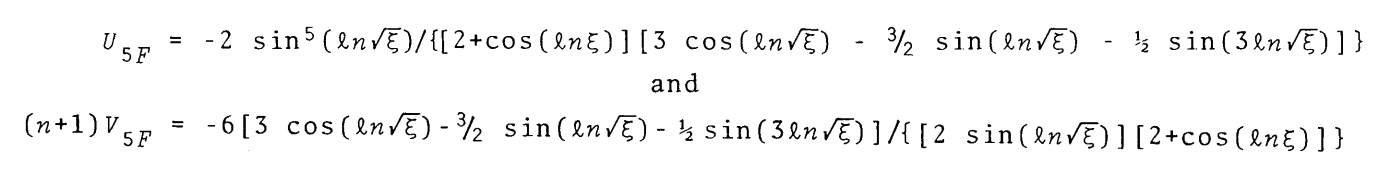Revision as of 18:56, 30 April 2015

BiPolytrope with <math>n_c = 1</math> and <math>n_e=5</math>

Here we construct a bipolytrope in which the core has an <math>~n_c=1</math> polytropic index and the envelope has an <math>~n_e=5</math> polytropic index. As in the case of our separately discussed, "mirror image" bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, this system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. [On 12 April 2015, J. E. Tohline wrote: I became aware of the published discussions of this system by Murphy — and especially the work of Murphy & Fiedler (1985) — (see itemization of additional key references, below) in March of 2015 after searching the internet for previous analyses of radial oscillations in polytropes and, then, reading through Horedt's (2004) §2.8.1 discussion of composite polytropes.]

Key References

S. Srivastava (1968, ApJ, 136, 680) A New Solution of the Lane-Emden Equation of Index n = 5
H. A. Buchdahl (1978, Australian Journal of Physics, 31, 115): Remark on the Polytrope of Index 5 — the result of this work by Buchdahl has been highlighted inside our discussion of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>.
J. O. Murphy (1980a, Proc. Astr. Soc. of Australia, 4, 37): A Finite Radius Solution for the Polytrope Index 5
J. O. Murphy (1980b, Proc. Astr. Soc. of Australia, 4, 41): On the F-Type and M-Type Solutions of the Lane-Emden Equation
J. O. Murphy (1981, Proc. Astr. Soc. of Australia, 4, 205): Physical Characteristics of a Polytrope Index 5 with Finite Radius
J. O. Murphy (1982, Proc. Astr. Soc. of Australia, 4, 376): A Sequence of E-Type Composite Analytical Solutions of the Lane-Emden Equation
J. O. Murphy (1983, Australian Journal of Physics, 36, 453): Structure of a Sequence of Two-Zone Polytropic Stellar Models with Indices 0 and 1
J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175): Composite and Analytical Solutions of the Lane-Emden Equation with Polytropic Indices n = 1 and n = 5
J. O. Murphy & R. Fiedler (1985a, Proc. Astr. Soc. of Australia, 6, 219): Physical Structure of a Sequence of Two-Zone Polytropic Stellar Models
J. O. Murphy & R. Fiedler (1985b, Proc. Astr. Soc. of Australia, 6, 222): Radial Pulsations and Vibrational Stability of a Sequence of Two-Zone Polytropic Stellar Models

Steps 2 & 3

Based on the discussion presented elsewhere of the structure of an isolated <math>n=1</math> polytrope, the core of this bipolytrope will have the following properties:

<math> \theta(\xi) = \frac{\sin\xi}{\xi} ~~~~\Rightarrow ~~~~ \theta_i = \frac{\sin\xi_i}{\xi_i} ; </math>

<math> \frac{d\theta}{d\xi} = \biggl[ \frac{\cos\xi}{\xi}- \frac{\sin\xi}{\xi^2}\biggr] ~~~~\Rightarrow ~~~~ \biggl(\frac{d\theta}{d\xi}\biggr)_i = \biggl[\frac{\cos\xi_i}{\xi_i}- \frac{\sin\xi_i}{\xi_i^2} \biggr] \, . </math>

The first zero of the function <math>~\theta(\xi)</math> and, hence, the surface of the corresponding isolated <math>~n=1</math> polytrope is located at <math>~\xi_s = \pi</math>. Hence, the interface between the core and the envelope can be positioned anywhere within the range, <math>~0 < \xi_i < \pi</math>.

Step 4: Throughout the core (<math>0 \le \xi \le \xi_i</math>)

Specify: <math>~K_c</math> and <math>~\rho_0 ~\Rightarrow</math>
<math>~\rho</math>	<math>~=</math>	<math>\rho_0 \theta^{n_c}</math>	<math>~=</math>	<math>~\rho_0 \biggl( \frac{\sin\xi}{\xi} \biggr)</math>
<math>~P</math>	<math>~=</math>	<math>~K_c \rho_0^{1+1/n_c} \theta^{n_c + 1}</math>	<math>~=</math>	<math>~K_c \rho_0^{2} \biggl( \frac{\sin\xi}{\xi}\biggr)^{2}</math>
<math>~r</math>	<math>~=</math>	<math>~\biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{1/2} \rho_0^{(1-n_c)/(2n_c)} \xi</math>	<math>~=</math>	<math>~\biggl[ \frac{K_c}{2\pi G} \biggr]^{1/2} \xi</math>
<math>~M_r</math>	<math>~=</math>	<math>~4\pi \biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{3/2} \rho_0^{(3-n_c)/(2n_c)} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math>	<math>~=</math>	<math>~4\pi \biggl[ \frac{K_c}{2\pi G} \biggr]^{3/2} \rho_0 \biggl[\sin\xi - \xi \cos\xi \biggr]</math>

Step 5: Interface Conditions

			Setting <math>~n_c=1</math>, <math>~n_e=5</math>, and <math>~\phi_i = \phi_i ~~~~\Rightarrow</math>
<math>~\frac{\rho_e}{\rho_0}</math>	<math>~=</math>	<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{n_c}_i \phi_i^{-n_e}</math>	<math>~=</math>	<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta_i \phi_i^{-5}</math>
<math>~\biggl( \frac{K_e}{K_c} \biggr) </math>	<math>~=</math>	<math>~\rho_0^{1/n_c - 1/n_e}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-(1+1/n_e)} \theta^{1 - n_c/n_e}_i</math>	<math>~=</math>	<math>~\biggl[\rho_0^{4}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-6} \theta^{4}_i\biggr]^{1/5}</math>
<math>~\frac{\eta_i}{\xi_i}</math>	<math>~=</math>	<math>~\biggl[ \frac{n_c + 1}{n_e+1} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{(n_c-1)/2} \phi_i^{(1-n_e)/2}</math>	<math>~=</math>	<math>~\biggl( \frac{1}{3} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \phi_i^{-2}</math>
<math>~\biggl( \frac{d\phi}{d\eta} \biggr)_i</math>	<math>~=</math>	<math>~\biggl[ \frac{n_c + 1}{n_e + 1} \biggr]^{1/2} \theta_i^{- (n_c + 1)/2} \phi_i^{(n_e+1)/2} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math>	<math>~=</math>	<math>~\biggl( \frac{1}{3} \biggr)^{1/2} \theta_i^{- 1} \biggl( \frac{d\theta}{d\xi} \biggr)_i \phi_i^3</math>

Alternative: In our introductory description of how to build a bipolytropic structure, we pointed out that, instead of employing these last two fitting conditions, Chandrasekhar [C67] found it useful to employ, instead, the ratio of the <math>3^\mathrm{rd}</math> to <math>4^\mathrm{th}</math> expressions, which in the present case produces,

<math> \frac{\eta_i \phi_i^{5}}{(d\phi/d\eta)_i} = \frac{\xi_i \theta_i}{(d\theta/d\xi)_i} \biggl( \frac{\mu_e}{\mu_c}\biggr) \, , </math>

and the product of the <math>3^\mathrm{rd}</math> and <math>4^\mathrm{th}</math> expressions, which in the present case generates,

<math> \frac{3\eta_i (d\phi/d\eta)_i}{ \phi_i } = \frac{\xi_i (d\theta/d\xi)_i}{ \theta_i } \biggl( \frac{\mu_e}{\mu_c}\biggr) \, . </math>

As is explained, immediately below, Murphy (1983) followed Chandrasekhar's lead and extracted fitting conditions from this last pair of expressions. In seeking the most compact analytic solution, we have found it advantageous to combine our standard <math>3^\mathrm{rd}</math> fitting expression with the last (i.e., the product) expression identified by Chandrasekhar.

Step 6: Envelope Solution

Following the work of Murphy (1983) and of Murphy & Fiedler (1985a), we will adopt for the envelope's structure the F-Type solution of the <math>~n=5</math> Lane-Emden function discovered by S. Srivastava (1968, ApJ, 136, 680) and described in an accompanying discussion, namely,

specifically over the physically viable interval, <math>~e^{2\pi} \ge A\eta \ge \eta_\mathrm{crit} \equiv e^{2\tan^{-1}(1+2^{1/3})} \, .</math> The first derivative of this function is,

<math>~ \frac{B^{-1}[3\cos\Delta-3\sin\Delta + 2\sin^3\Delta] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} \, , </math>

where,

<math>~\Delta \equiv \ln(A\eta)^{1/2} = \ln A^{1/2} + \ln\eta^{1/2} \, .</math>

ASIDE: Comments on Presentation by Murphy (1983)

As presented by Murphy (1983), most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are:

<math>~U_{5F} \equiv \eta \phi^5 \biggl(- \frac{d\phi}{d\eta}\biggr)^{-1}</math>	<math>~=</math>	<math>~ \frac{B^{-4}\eta \sin^5\Delta}{\eta^{5/2}\{3-2\sin^2\Delta\}^{5/2}} \biggl[ \frac{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}}{3\sin\Delta - 2\sin^3\Delta -3\cos\Delta } \biggr] </math>
	<math>~=</math>	<math>~ \frac{2B^{-4}\sin^5\Delta}{[3-2\sin^2\Delta][3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ]} </math>
	<math>~=</math>	<math>~ \frac{-2B^{-4}\sin^5\Delta}{[2+\cos(2\Delta)][3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ]} \, ; </math>
<math>~V_{5F} \equiv \frac{\eta}{ \phi} \biggl(- \frac{d\phi}{d\eta}\biggr)</math>	<math>~=</math>	<math>~\frac{\eta^{3/2}\{3-2\sin^2\Delta\}^{1/2}} {\sin\Delta} \frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} </math>
	<math>~=</math>	<math>~\frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\sin\Delta (3-2\sin^2\Delta)} </math>
	<math>~=</math>	<math>~\frac{-[3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ] }{2\sin\Delta [2+\cos(2\Delta)]} \, . </math>

After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by Murphy (1983) and reproduced (slightly edited) here as an image, for ease of comparison:

U_5F and V_5F Functions by Murphy (1983)

First Constraint

Calling upon Chandrasekhar's "product" expression, as just defined above, one fitting condition at the interface is,

<math>~- \frac{2\xi_i }{ 3\theta_i } \biggl( \frac{d\theta}{d\xi} \biggr)_i \biggl( \frac{\mu_e}{\mu_c}\biggr)</math>	<math>~=</math>	<math>~2\biggl( V_{5F} \biggr)_i </math>
	<math>~=</math>	<math>~\frac{[3\sin\Delta_i - 2\sin^3\Delta_i -3\cos\Delta_i ] }{\sin\Delta_i (3-2\sin^2\Delta_i)}</math>
	<math>~=</math>	<math>~\frac{3 - 2\sin^2\Delta_i -3\cot\Delta_i}{(3-2\sin^2\Delta_i)} \, .</math>

The left-hand side of this expression is inherently positive over the physically viable radial coordinate range, <math>~0 \ge \xi_i \ge \pi</math> and its value is known once the radial coordinate of the edge of the core has been specified. So, defining the interface parameter,

<math>~ \kappa_i \equiv - \frac{2\theta_i^' \xi_i}{3\theta_i} \biggl( \frac{\mu_e}{\mu_c} \biggr) \, ,</math>

and, as in our separate discussion of the properties of Srivastava's function, adopting the shorthand notation,

<math>~y_i \equiv \tan\Delta_i \, ,</math>

this interface condition becomes,

<math>~\kappa_i</math>	<math>~=</math>	<math>~ \frac{3 - 2y_i^2(1+y_i^2)^{-1}- 3y_i^{-1} }{3-2y_i^2(1+y_i^2)^{-1}} </math>
	<math>~=</math>	<math>~ \frac{3y_i(1+y_i^2)- 2y_i^3 -3(1+y_i^2)}{3y_i(1+y_i^2)-2y_i^3} </math>
	<math>~=</math>	<math>~ \frac{y_i^3 -3y_i^2 + 3y_i -3 }{3y_i+y_i^3} </math>
<math>~\Rightarrow~~~~ \kappa_i(3y_i+y_i^3)</math>	<math>~=</math>	<math>~ y_i^3 -3y_i^2 + 3y_i -3 </math>
<math>~\Rightarrow~~~~ y_i^3(1-\kappa_i) -3 y_i^2 + 3(1-\kappa_i)y_i -3</math>	<math>~=</math>	<math>~ 0 \, . </math>

ASIDE: Analytic Solution of Cubic Equation

As is well known and documented — see, for example Wolfram MathWorld or Wikipedia's discussion of the topic — the roots of any cubic equation can be determined analytically. In order to evaluate the root(s) of our particular cubic equation, we have drawn from the utilitarian online summary provided by Eric Schechter at Vanderbilt University. For a cubic equation of the general form,

a real root is given by the expression,

where,

<math>~p \equiv -\frac{b}{3a} \, ,</math> <math>~q \equiv \biggl[p^3 + \frac{bc-3ad}{6a^2} \biggr] \, ,</math> and <math>~r=\frac{c}{3a} \, .</math>

In our particular case,

<math>~a =(1-\kappa_i)\, ,</math> <math>~b =-3\, ,</math> <math>~c = 3(1-\kappa_i) \, ,</math> and <math>~d = - 3 \, .</math>

Hence,

<math>~p = \frac{1}{(1-\kappa_i)} \, ,</math> <math>~r=+1 \, ,</math> and <math>~q = p^3 = \frac{1}{(1-\kappa_i)^3} \, ,</math>

which implies that the real root, <math>~y_\mathrm{root}</math>, is given by the expression,

<math>~y_\mathrm{root}</math>	<math>~=</math>	<math>~ p + \{p^3 + [p^6 + (1-p^2)^3]^{1/2}\}^{1/3} + \{p^3 - [p^6 + (1-p^2)^3]^{1/2}\}^{1/3} </math>
	<math>~=</math>	<math>~ p + \{p^3 + p^3[1 + (p^{-2}-1)^3]^{1/2}\}^{1/3} + \{p^3 - p^3[1 + (p^{-2}-1)^3]^{1/2}\}^{1/3} </math>
<math>~\Rightarrow ~~~~ p^{-1} y_\mathrm{root}</math>	<math>~=</math>	<math>~ 1 + \{1 + [1 + (p^{-2}-1)^3]^{1/2}\}^{1/3} + \{1 - [1 + (p^{-2}-1)^3]^{1/2}\}^{1/3} \, . </math>

(There is also a pair of imaginary roots, but they are irrelevant in the context of our overarching astrophysical discussion.)

In summary, then,

Once the location, <math>~\xi_i</math>, of the outer edge of the core has been specified, which determines <math>~\theta_i</math> and <math>~\theta^'_i</math> as well, the value of the parameters, <math>~\kappa_i</math> and <math>~p</math>, are known via the expressions,

<math>~\kappa_i \equiv - \frac{2\theta_i^' \xi_i}{3\theta_i} \biggl( \frac{\mu_e}{\mu_c} \biggr)</math>

<math>~\frac{2}{3} \biggl(1 - \xi_i \cot\xi_i \biggr)\biggl( \frac{\mu_e}{\mu_c} \biggr) \, ,</math>

and,

<math>~p \equiv (1-\kappa_i)^{-1} </math>

The value of <math>~y_\mathrm{root}</math> is determined from the just-derived solution to the governing cubic equation, which then gives the interface value of the envelope parameter (adjusted by a <math>~\pi m</math> phase angle, where <math>~m</math> is an, as yet unspecified, integer),

<math>~\Delta_i = \tan^{-1}(y_\mathrm{root}) +\pi m \, .</math>

This, in turn, can be interpreted as a coordinate root — which we shall refer to as <math>~\eta_\mathrm{root}</math> — via the expression,

<math>~(A\eta)_\mathrm{root} = e^{2\Delta_i} = e^{2\pi m} \cdot e^{2\tan^{-1}(y_\mathrm{root})} \, .</math>

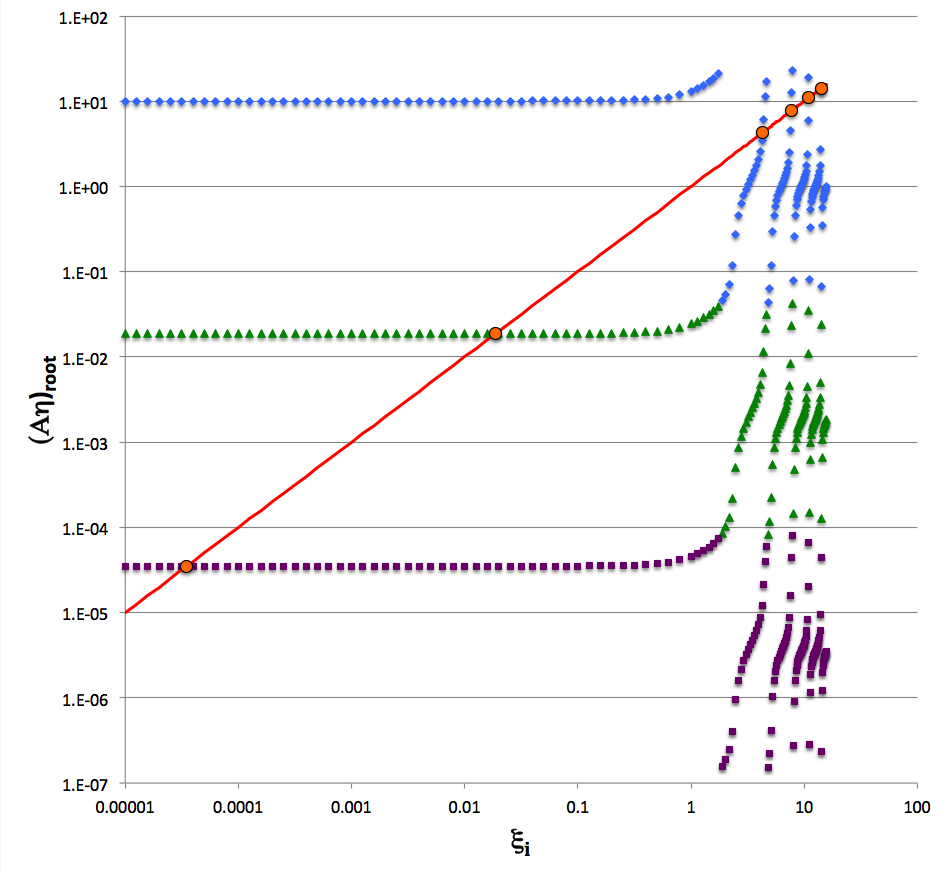
The following log-log plot shows what value(s) of <math>~(A\eta)_\mathrm{root} </math> (vertical axis) result from a wide range of interface coordinate specifications, <math>~\xi_i</math> (horizontal axis), under the simplifying assumption that <math>~(\mu_e/\mu_c) = 1</math>; solid blue diamonds identify roots resulting from setting <math>~m=0</math> in the phase-shift specification, solid green triangles identify roots for which <math>~m=-1</math>, and solid purple squares identify roots for which <math>~m=-2</math>. Notice that when <math>~\xi_i \ll 1</math> — and, hence, <math>~\kappa_i \ll 1</math> and <math>~p \rightarrow 1</math>,

<math>~y_\mathrm{root} \rightarrow (1 + 2^{1/3}) ~~~~~~~ \Rightarrow ~~~~~~~ (A\eta)_\mathrm{root} \rightarrow e^{2\pi m} \cdot e^{2\tan^{-1}(1 + 2^{1/3})} = 10.05837e^{2\pi m} \, .</math>

Hence, as displayed in the figure, the curve traced by blue diamonds (m = 0) asymptotically approaches (to the left) <math>~10.05837</math>; the curve traced by green triangles (m = -1) asymptotically approaches <math>1.87834\times 10^{-2}</math>; and the curve traced by purple squares (m = -2) asymptotically approaches <math>3.50770\times 10^{-5}</math>.

Examination of F2 Function Discussed by J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175)

Murphy's

Roots of

F2 = 0

Function

3.5076E-05

1.8785E-02

4.2993E+00

7.6882E+00

1.0913E+01

1.4101E+01

The red line in the figure shows where the coordinate value along the vertical axis equals the coordinate value along the horizontal axis. Hence the points where this red line intersects the other curves in the figure can be interpreted as identifying solutions to the cubic equation for which <math>~A = 1</math>, and,

<math>~\eta_\mathrm{root} = \xi_i \, .</math>

These points are also what Murphy (1983) refers to as roots of his <math>~F2 = 0</math> function. The values of ten successive coordinate roots of this function are listed in the right-hand column of Table 1 in Murphy (1983). We have re-listed the values of six of these roots in a column immediately to the right of the above figure and have marked with orange circles the locations of these six points in the figure. As they should, Murphy's identified roots lie precisely at the intersection of the red line with the other curves.

Murphy's Example Model Characteristics

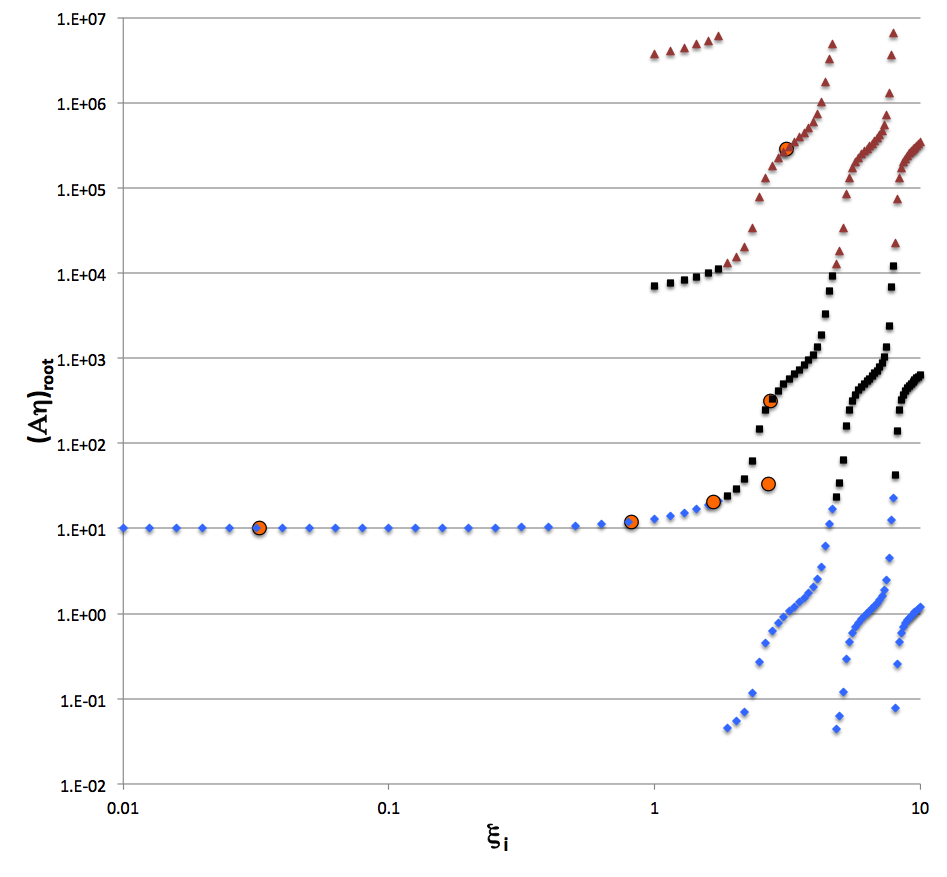
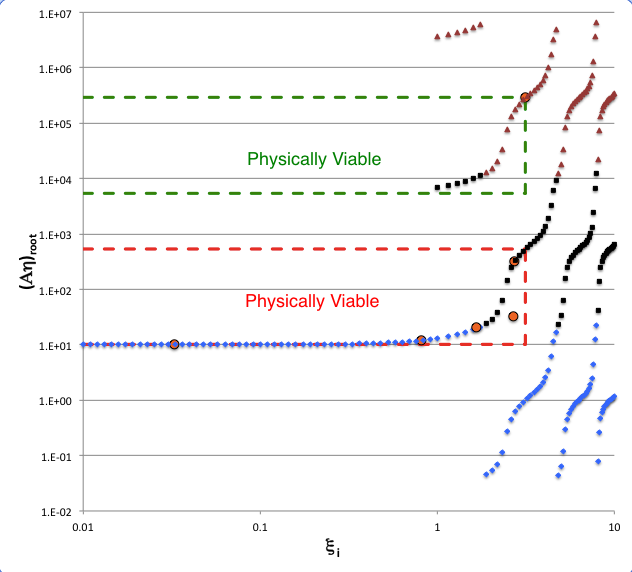
As in the previous figure, the following log-log plot shows what value(s) of <math>~(A\eta)_\mathrm{root} </math> (vertical axis) result from a wide range of interface coordinate specifications, <math>~\xi_i</math> (horizontal axis), under the simplifying assumption that <math>~(\mu_e/\mu_c) = 1</math>. The solid blue diamonds present exactly the same information as in the previous figure, that is, they identify roots resulting from setting <math>~m=0</math> in the phase-shift specification. But here, focusing on a regime that highlights larger roots of the first constraint equation, solid black squares identify roots for which <math>~m=+1</math>, and solid maroon triangles identify roots for which <math>~m=+2</math>.

Examination of Table 3 Data Presented in J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175)

Table 3 Model Characteristics by Murphy (1983)

Murphy's Table 3 Data
<math>~\zeta_J \rightarrow \xi_i</math>	<math>~\xi_J \rightarrow (A\eta)_\mathrm{root}</math>
3.2678E-02	10.0164
0.8154	12.0083
1.6598	20.4312
2.6914	33.0249
2.7302	100<math>\pi</math>
3.1415	91275<math>\pi</math>

In his Table 3, Murphy (1983) presents six pairs of "coordinate" roots, <math>~(\zeta_J, \xi_J)</math>, that not only satisfy the first constraint equation but that also, in his interpretation, identify physically viable model solutions. The values of all six of these coordinate pairs have been re-listed immediately to the right of the log-log plot, in a separate panel of the above figure. After mapping Murphy's coordinate notation to ours — specifically invoking the mapping <math>~(\zeta_J, \xi_J) ~\rightarrow~ (\xi_i, A\eta_\mathrm{root})</math> — the locations of all six models have been marked by orange circles on the plot. Five of Murphy's models fall directly onto our generated curves, giving us considerable confidence that our analysis matches his in considerable detail. As is explained more fully, below, we strongly suspect that the single Murphy model that does not lie on one of our generated curves — the one which, as published in Murphy's Table 3, has coordinates<math>~(\zeta_J, \xi_J) = (2.6914, 33.0249)</math> — is misplaced because of a typographical error in the published table.

As a supplement to the preceding two figures, the following table shows in quantitative detail how we are able to analytically derive individual coordinate roots, <math>~(A\eta)_\mathrm{root}</math> — see the next-to-last column of the table — from ten different interface-coordinate locations, <math>~\xi_i = \zeta_J</math>, as specified in the first (left-most) column of the table. The interface parameter, <math>~\kappa_i</math>, is determined directly from the specified value of <math>~\xi_i</math>; the parameter, <math>~p=(1-\kappa_i)^{-1}</math>; then, given <math>~p</math>, the root to the cubic equation and, in turn, the value of <math>~\Delta_i</math>, are determined; and, finally, a choice of the integer phase-shift parameter, <math>~m</math>, leads to the calculation of <math>~(A\eta)_\mathrm{root}</math>. For comparison, the last (right-most) column of the table lists the corresponding coordinate, <math>~\xi_J</math>, as originally derived and published by Murphy (1983). Coordinate pairs shown in the orange-colored panels of our table correspond to the six models whose characteristics are provided in Murphy's Table 3; coordinate pairs shown in the green-colored panels correspond to two of the ten "F2 = 0" roots identified in Murphy's Table 1; and the additional three coordinate pairs shown in the blue-colored panels have been drawn from Murphy's Table 2.

Murphy (1983) Tables 1, 2, & 3	Here … setting <math>\xi_i = \zeta_J</math> … and assuming <math>\mu_e/\mu_c = 1</math>						Murphy (1983) Tables 1, 2, & 3
Murphy (1983) Tables 1, 2, & 3	1^st Constraint						Murphy (1983) Tables 1, 2, & 3
<math>~\zeta_J</math>	<math>~\kappa_i</math>	<math>~p</math>	<math>~y_\mathrm{root}</math>	<math>~\Delta_i = \tan^{-1}(y_\mathrm{root})</math>	<math>~m </math>	<math>~(A\eta)_\mathrm{root} = e^{2(\Delta_i + m\pi)}</math>	<math>~\xi_J</math>
3.2678E-02	2.3732E-04	1.00023737	2.26083	1.15435	-3	6.55237E-08	6.55E-08
					-2	3.50874E-05	3.508E-05
					-1	1.87890E-02	1.8789E-02
					0	10.0614	10.0164
0.8154	0.15474	1.18307	2.93939	1.24287	0	12.0101	12.0083
1.6598	0.76541	4.26281	12.6311	1.49179	0	19.7585	20.4312
[ 2.0914 ]	1.46609	-2.14552	-6.11816	-1.40878	1	31.9964	33.0249
[ 2.10961 ]	1.50744	-1.97067	-5.56379	-1.39296	1	33.0249
2.6914	4.37925	-0.29592	-0.31486	-0.30503	1	290.943
2.7302	4.83853	-0.26052	-0.27316	-0.26666	1	99.997<math>\pi</math>	100<math>\pi</math>
3.1415	22604.6	-4.42408E-05	-4.42408E-05	-4.42408E-05	2	91268<math>\pi</math>	91275<math>\pi</math>
4.2993	-0.58961	0.62908	0.89355	0.72924	0	4.2994	4.2993
7.6882	-0.19091	0.83969	1.6268	1.01964	0	7.6851	7.6882

As this table and its two preceding figures illustrate, by and large, the agreement between our analytically determined coordinate roots and those derived & published by Murphy (1983) is excellent. There are a couple of mismatches, but we attribute both to typesetting errors in the Murphy publication:

The coordinate, <math>~\xi_J = 10.0164</math>, that has been displayed using a red font in the right-most column of our table is the value drawn directly from Murphy's Table 3. It appears to us that two digits of this number were inadvertently transposed during publication and that the coordinate value should have appeared as <math>~\xi_J = 10.0614</math>. We are convinced that, as published, this is a typographical error in Murphy's Table 3 because: (a) the corrected value matches our derived value of that coordinate to more significant figures, and (b) the same model is also listed in Murphy's Table 2 with this corrected value.
The coordinate, <math>~\zeta_J = 2.6914</math>, that has been displayed using a red font in the left-most column of our table is the value drawn directly from Murphy's Table 3. As shown in our table, from this coordinate value we derive a root coordinate of <math>~(A\eta)_\mathrm{root} = 290.943</math>, which is almost a factor of ten larger than Murphy's published root coordinate value, <math>~\xi_J = 33.0249</math>. Working backwards via an iterative procedure, we have determined that Murphy's listed root of <math>33.0249</math> can be obtained if the originating value of <math>~\zeta_J \leftrightarrow \xi_i</math> is set to <math>2.10961</math> (see the black-on-white panel entry in the left-most column of our table). By replacing the "6" by a zero in Murphy's published coordinate parameter — that is, by assuming that there was a typographical error and Murphy's interface coordinate was actually <math>~\zeta_J = 2.0914</math>, we are able to derive a root coordinate value (31.9964) that is quite close to Murphy's published value (33.0249).

If, following Murphy's lead, we now consider the dimensionless radial variable throughout the <math>~n=5</math> envelope, <math>~\eta</math>, to be simply a direct extension of the dimensionless radial variable, <math>~\xi</math>, that is used throughout the <math>~n=1</math> core — in which case, the interface between the core and the envelope is not just associated with <math>~\xi_i</math>, but also with <math>~\eta_\mathrm{root} = \xi_i</math> — then the so-called homology factor, <math>~A</math>, in Srivastava's Lane-Emden function expression can be determined for each tabulated interface coordinate pair via the ratio,

<math>~A = \frac{(A\eta)_\mathrm{root}}{\xi_i} \, .</math>

Furthermore, it is clear that the surface of the bipolytropic configuration is identified by the value of the radial coordinate, <math>~\xi_s = \eta_s</math>, at which the numerator of Srivastava's function, <math>~\phi</math>, drops to zero. That is, the surface occurs where,

<math>~\Delta_s</math>	<math>~=</math>	<math>~\pi</math>
<math>~\Rightarrow ~~~~\xi_s = \eta_s</math>	<math>~=</math>	<math>~\frac{1}{A} \cdot e^{2(m+1)\pi} \, .</math>

We can now construct a table of model characteristics that is patterned after and largely matches Murphy's (1983) Table 3, with only the overall scaling parameter, <math>~B</math>, yet to be determined.

Some Model Characteristics
Model	Specified		Analytically Determined Here
Model	<math>~\xi_i</math>	<math>~m</math>	<math>~(A\eta)_\mathrm{root}</math>	<math>~A</math>	<math>~B</math>	<math>~\xi_s</math>
1	3.2678E-02	0	10.0614	307.895	---	1.7392
2	0.8154	0	12.0101	14.729	---	36.356
3	1.6598	0	19.7585	11.9041	---	44.9836
4	2.0914	0	31.9964	15.2990	---	35.0017
5	2.7302	0	99.997<math>\pi</math>	115.065	---	4.6538
6	3.1415	1	91268<math>\pi</math>	170.443<math>e^{2\pi}</math>	---	3.1418

Physically Viable Parameter Regime

Second Constraint

Obtained from Third Interface Condition

Now, our 3^rd interface condition, as detailed above, states that,

<math>~\frac{\eta_i}{\xi_i}</math>	<math>~=</math>	<math>~3^{-1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr) \phi_i^{-2}</math>
	<math>~=</math>	<math>~3^{-1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[ \frac{\eta^{1/2} (3-2\sin^2\Delta_i)^{1/2}}{B^{-1}\sin\Delta_i} \biggr]^{2} </math>
<math>~\Rightarrow ~~~~ B^2</math>	<math>~=</math>	<math>~\frac{\sqrt{3}}{\xi_i} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \biggl( \frac{3}{\sin^2\Delta_i} - 2\biggr)^{-1} \, . </math>

Obtained from Chandrasekhar's U-constraint

We shall now demonstrate that the same expression for the scaling coefficient, <math>~B</math>, can alternatively be obtained from Chandrasekhar's "U" constraint after taking into account the result that already has been obtained from the "V" constraint. As described above, the "U" constraint is an alternative interface condition that may be written as,

<math>~\frac{\xi_i \theta_i}{(-d\theta/d\xi)_i} \biggl( \frac{\mu_e}{\mu_c}\biggr)</math>

which, in the particular case being examined here, becomes,

<math>~\frac{2\xi_i^2}{3\kappa_i} \biggl( \frac{\mu_e}{\mu_c}\biggr)^2 </math>	<math>~=</math>	<math>~\biggl( U_\mathrm{5F} \biggr)_i </math>
	<math>~=</math>	<math>~ \frac{2B^{-4} \sin^4\Delta_i}{(3-2\sin^2\Delta_i)(3 - 2\sin^2\Delta_i - 3\cot\Delta_i)} \, . </math>

Now, from our discussion, above, of the first constraint, we know that,

<math>~(3 - 2\sin^2\Delta_i - 3\cot\Delta_i)</math>

<math>~(3-2\sin^2\Delta_i)\kappa_i \, .</math>

Hence, Chandrasekhar's U-constraint becomes,

<math>~\frac{2\xi_i^2}{3\kappa_i} \biggl( \frac{\mu_e}{\mu_c}\biggr)^2 </math>	<math>~=</math>	<math>~ \frac{2B^{-4} \sin^4\Delta_i}{(3-2\sin^2\Delta_i)^2 \kappa_i} </math>
<math>~\Rightarrow ~~~~ B^4 </math>	<math>~=</math>	<math>~ \frac{3\sin^4\Delta_i}{\xi_i^2 (3-2\sin^2\Delta_i)^2} \biggl( \frac{\mu_e}{\mu_c}\biggr)^{-2} </math>
<math>~\Rightarrow ~~~~ B^2</math>	<math>~=</math>	<math>~\frac{\sqrt{3}}{\xi_i} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \biggl( \frac{3}{\sin^2\Delta_i} - 2\biggr)^{-1} \, ,</math>

which, as predicted, is identical to what we learned from the third interface condition, alone.

Related Discussions

@@ Line 1,213: / Line 1,213: @@
 </tr>
 <tr>
-   <td align="center">
+   <td align="center" rowspan="2">
 Model
    </td>
+  <td align="center" colspan="2">
+Specified
+  </td>
+  <td align="center" colspan="4">
+Analytically Determined Here
+  </td>
+</tr>
+<tr>
    <td align="center">
 <math>~\xi_i</math>

Difference between revisions of "User:Tohline/SSC/Structure/BiPolytropes/Analytic1 5"