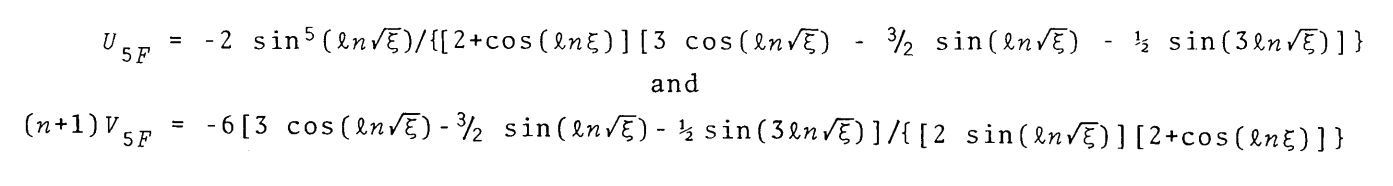User:Tohline/SSC/Structure/BiPolytropes/Analytic1 5

BiPolytrope with <math>n_c = 1</math> and <math>n_e=5</math>

Here we construct a bipolytrope in which the core has an <math>~n_c=1</math> polytropic index and the envelope has an <math>~n_e=5</math> polytropic index. As in the case of our separately discussed, "mirror image" bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, this system is particularly interesting because the entire structure can be described by closed-form, analytic expressions. [On 12 April 2015, J. E. Tohline wrote: I became aware of the published discussions of this system by Murphy — and especially the work of Murphy & Fiedler (1985) — (see itemization of additional key references, below) in March of 2015 after searching the internet for previous analyses of radial oscillations in polytropes and, then, reading through Horedt's (2004) §2.8.1 discussion of composite polytropes.]

Key References

• S. Srivastava (1968, ApJ, 136, 680) A New Solution of the Lane-Emden Equation of Index n = 5
• H. A. Buchdahl (1978, Australian Journal of Physics, 31, 115): Remark on the Polytrope of Index 5 — the result of this work by Buchdahl has been highlighted inside our discussion of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>.
• J. O. Murphy (1980a, Proc. Astr. Soc. of Australia, 4, 37): A Finite Radius Solution for the Polytrope Index 5
• J. O. Murphy (1980b, Proc. Astr. Soc. of Australia, 4, 41): On the F-Type and M-Type Solutions of the Lane-Emden Equation
• J. O. Murphy (1981, Proc. Astr. Soc. of Australia, 4, 205): Physical Characteristics of a Polytrope Index 5 with Finite Radius
• J. O. Murphy (1982, Proc. Astr. Soc. of Australia, 4, 376): A Sequence of E-Type Composite Analytical Solutions of the Lane-Emden Equation
• J. O. Murphy (1983, Australian Journal of Physics, 36, 453): Structure of a Sequence of Two-Zone Polytropic Stellar Models with Indices 0 and 1
• J. O. Murphy (1983, Proc. Astr. Soc. of Australia, 5, 175): Composite and Analytical Solutions of the Lane-Emden Equation with Polytropic Indices n = 1 and n = 5
• J. O. Murphy & R. Fiedler (1985a, Proc. Astr. Soc. of Australia, 6, 219): Physical Structure of a Sequence of Two-Zone Polytropic Stellar Models
• J. O. Murphy & R. Fiedler (1985b, Proc. Astr. Soc. of Australia, 6, 222): Radial Pulsations and Vibrational Stability of a Sequence of Two-Zone Polytropic Stellar Models

Steps 2 & 3

Based on the discussion presented elsewhere of the structure of an isolated <math>n=1</math> polytrope, the core of this bipolytrope will have the following properties:

<math> \theta(\xi) = \frac{B\sin\xi}{\xi} ~~~~\Rightarrow ~~~~ \theta_i = \frac{B\sin\xi_i}{\xi_i} ; </math>

<math> \frac{d\theta}{d\xi} = B\biggl[ \frac{\cos\xi}{\xi}- \frac{\sin\xi}{\xi^2}\biggr] ~~~~\Rightarrow ~~~~ \biggl(\frac{d\theta}{d\xi}\biggr)_i = B\biggl[\frac{\cos\xi_i}{\xi_i}- \frac{\sin\xi_i}{\xi_i^2} \biggr] \, . </math>

The first zero of the function <math>~\theta(\xi)</math> and, hence, the surface of the corresponding isolated <math>~n=1</math> polytrope is located at <math>~\xi_s = \pi</math>. Hence, the interface between the core and the envelope can be positioned anywhere within the range, <math>~0 < \xi_i < \pi</math>.

Step 4: Throughout the core (<math>0 \le \xi \le \xi_i</math>)

Specify: <math>~K_c</math> and <math>~\rho_0 ~\Rightarrow</math>
<math>~\rho</math>	<math>~=</math>	<math>\rho_0 \theta^{n_c}</math>	<math>~=</math>	<math>~\rho_0 \biggl( \frac{B\sin\xi}{\xi} \biggr)</math>
<math>~P</math>	<math>~=</math>	<math>~K_c \rho_0^{1+1/n_c} \theta^{n_c + 1}</math>	<math>~=</math>	<math>~K_c \rho_0^{2} \biggl( \frac{B\sin\xi}{\xi}\biggr)^{2}</math>
<math>~r</math>	<math>~=</math>	<math>~\biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{1/2} \rho_0^{(1-n_c)/(2n_c)} \xi</math>	<math>~=</math>	<math>~\biggl[ \frac{K_c}{2\pi G} \biggr]^{1/2} \xi</math>
<math>~M_r</math>	<math>~=</math>	<math>~4\pi \biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{3/2} \rho_0^{(3-n_c)/(2n_c)} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math>	<math>~=</math>	<math>~4\pi \biggl[ \frac{K_c}{2\pi G} \biggr]^{3/2} \rho_0 B\biggl[\sin\xi - \xi \cos\xi \biggr]</math>

Step 5: Interface Conditions

			Setting <math>~n_c=1</math>, <math>~n_e=5</math>, and <math>~\phi_i = \phi_i ~~~~\Rightarrow</math>
<math>~\frac{\rho_e}{\rho_0}</math>	<math>~=</math>	<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{n_c}_i \phi_i^{-n_e}</math>	<math>~=</math>	<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta_i \phi_i^{-5}</math>
<math>~\biggl( \frac{K_e}{K_c} \biggr) </math>	<math>~=</math>	<math>~\rho_0^{1/n_c - 1/n_e}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-(1+1/n_e)} \theta^{1 - n_c/n_e}_i</math>	<math>~=</math>	<math>~\biggl[\rho_0^{4}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-6} \theta^{4}_i\biggr]^{1/5}</math>
<math>~\frac{\eta_i}{\xi_i}</math>	<math>~=</math>	<math>~\biggl[ \frac{n_c + 1}{n_e+1} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{(n_c-1)/2} \phi_i^{(1-n_e)/2}</math>	<math>~=</math>	<math>~\biggl( \frac{1}{3} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \phi_i^{-2}</math>
<math>~\biggl( \frac{d\phi}{d\eta} \biggr)_i</math>	<math>~=</math>	<math>~\biggl[ \frac{n_c + 1}{n_e + 1} \biggr]^{1/2} \theta_i^{- (n_c + 1)/2} \phi_i^{(n_e+1)/2} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math>	<math>~=</math>	<math>~\biggl( \frac{1}{3} \biggr)^{1/2} \theta_i^{- 1} \biggl( \frac{d\theta}{d\xi} \biggr)_i \phi_i^3</math>

Alternative: In our introductory description of how to build a bipolytropic structure, we pointed out that, instead of employing these last two fitting conditions, Chandrasekhar [C67] found it useful to employ, instead, the ratio of the <math>3^\mathrm{rd}</math> to <math>4^\mathrm{th}</math> expressions, which in the present case produces,

<math> \frac{\eta_i \phi_i^{5}}{(d\phi/d\eta)_i} = \frac{\xi_i \theta_i}{(d\theta/d\xi)_i} \biggl( \frac{\mu_e}{\mu_c}\biggr) \, , </math>

and the product of the <math>3^\mathrm{rd}</math> and <math>4^\mathrm{th}</math> expressions, which in the present case generates,

<math> \frac{3\eta_i (d\phi/d\eta)_i}{ \phi_i } = \frac{\xi_i (d\theta/d\xi)_i}{ \theta_i } \biggl( \frac{\mu_e}{\mu_c}\biggr) \, . </math>

As is explained, immediately below, Murphy (1983) followed Chandrasekhar's lead and extracted fitting conditions from this last pair of expressions. In seeking the most compact analytic solution, we have found it advantageous to combine our standard <math>3^\mathrm{rd}</math> fitting expression with the last (i.e., the product) expression identified by Chandrasekhar.

Step 6: Envelope Solution

Following the work of Murphy (1983) and of Murphy & Fiedler (1985a), we will adopt for the envelope's structure the F-Type solution of the <math>~n=5</math> Lane-Emden function discovered by S. Srivastava (1968, ApJ, 136, 680) and described in an accompanying discussion, namely,

<math>~\phi</math>

<math>~=</math>

<math>~\frac{B\sin[\ln(A\eta)^{1/2})]}{\eta^{1/2}\{3-2\sin^2[\ln(A\eta)^{1/2}]\}^{1/2}} \, ,</math>

specifically over the physically viable interval, <math>~e^{2\pi} \ge A\eta \ge \eta_\mathrm{crit} \equiv e^{2\tan^{-1}(1+2^{1/3})} \, .</math> The first derivative of this function is,

<math>~\frac{d\phi}{d\eta}</math>

<math>~=</math>

<math>~ \frac{B[3\cos\Delta-3\sin\Delta + 2\sin^3\Delta] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} \, , </math>

where,

<math>~\Delta \equiv \ln(A\eta)^{1/2} = \ln A^{1/2} + \ln\eta^{1/2} \, .</math>

ASIDE: Comments on Presentation by Murphy (1983)

As presented by Murphy (1983), most of the development and analysis of this model was conducted within the framework of what is commonly referred to in the astrophysics community as the "U-V" plane. Specifically in the context of the model's <math>~n=5</math> envelope, this pair of referenced functions are: <math>~U_{5F} \equiv \eta \phi^5 \biggl(- \frac{d\phi}{d\eta}\biggr)^{-1}</math> <math>~=</math> <math>~ \frac{B^4\eta \sin^5\Delta}{\eta^{5/2}\{3-2\sin^2\Delta\}^{5/2}} \biggl[ \frac{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}}{3\sin\Delta - 2\sin^3\Delta -3\cos\Delta } \biggr] </math>   <math>~=</math> <math>~ \frac{2B^4\sin^5\Delta}{[3-2\sin^2\Delta][3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ]} </math>   <math>~=</math> <math>~ \frac{-2B^4\sin^5\Delta}{[2+\cos(2\Delta)][3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ]} \, ; </math> <math>~V_{5F} \equiv \frac{\eta}{ \phi} \biggl(- \frac{d\phi}{d\eta}\biggr)</math> <math>~=</math> <math>~\frac{\eta^{3/2}\{3-2\sin^2\Delta\}^{1/2}} {\sin\Delta} \frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\eta^{3/2}(3-2\sin^2\Delta)^{3/2}} </math>   <math>~=</math> <math>~\frac{[3\sin\Delta - 2\sin^3\Delta -3\cos\Delta ] }{2\sin\Delta (3-2\sin^2\Delta)} </math>   <math>~=</math> <math>~\frac{-[3\cos\Delta - \frac{3}{2}\sin\Delta - \frac{1}{2}\sin(3\Delta) ] }{2\sin\Delta [2+\cos(2\Delta)]} \, . </math> After recognizing that <math>~\cos(2\Delta) = \cos(2\ln\eta^{1/2}) = \cos(\ln\eta)\, ,</math> we see that these expressions for the functions, <math>~U_{5F}</math> and <math>~V_{5F}</math>, match the expressions used by Murphy (1983) and reproduced (slightly edited) here as an image, for ease of comparison:

First Constraint

Calling upon Chandrasekhar's "product" expression, as just defined above, one fitting condition at the interface is,

<math>~- \frac{2\xi_i }{ 3\theta_i } \biggl( \frac{d\theta}{d\xi} \biggr)_i \biggl( \frac{\mu_e}{\mu_c}\biggr)</math>	<math>~=</math>	<math>~2\biggl( V_{5F} \biggr)_i </math>
	<math>~=</math>	<math>~\frac{[3\sin\Delta_i - 2\sin^3\Delta_i -3\cos\Delta_i ] }{\sin\Delta_i (3-2\sin^2\Delta_i)}</math>
	<math>~=</math>	<math>~\frac{3 - 2\sin^2\Delta_i -3\cot\Delta_i}{(3-2\sin^2\Delta_i)} \, .</math>

The left-hand side of this expression is inherently positive over the physically viable radial coordinate range, <math>~0 \ge \xi_i \ge \pi</math> and its value is known once the radial coordinate of the edge of the core has been specified. So, defining the interface parameter,

<math>~ \kappa_i \equiv - \frac{2\theta_i^' \xi_i}{3\theta_i} \biggl( \frac{\mu_e}{\mu_c} \biggr) \, ,</math>

and, as in our separate discussion of the properties of Srivastava's function, adopting the shorthand notation,

<math>~y_i \equiv \tan\Delta_i \, ,</math>

this interface condition becomes,

<math>~\kappa_i</math>	<math>~=</math>	<math>~ \frac{3 - 2y_i^2(1+y_i^2)^{-1}- 3y_i^{-1} }{3-2y_i^2(1+y_i^2)^{-1}} </math>
	<math>~=</math>	<math>~ \frac{3y_i(1+y_i^2)- 2y_i^3 -3(1+y_i^2)}{3y_i(1+y_i^2)-2y_i^3} </math>
	<math>~=</math>	<math>~ \frac{y_i^3 -3y_i^2 + 3y_i -3 }{3y_i+y_i^3} </math>
<math>~\Rightarrow~~~~ \kappa_i(3y_i+y_i^3)</math>	<math>~=</math>	<math>~ y_i^3 -3y_i^2 + 3y_i -3 </math>
<math>~\Rightarrow~~~~ y_i^3(1-\kappa_i) -3 y_i^2 + 3(1-\kappa_i)y_i -3</math>	<math>~=</math>	<math>~ 0 \, . </math>

ASIDE: Analytic Solution of Cubic Equation

As is well known and documented — see, for example Wolfram MathWorld or Wikipedia's discussion of the topic — the roots of any cubic equation can be determined analytically. In order to evaluate the root(s) of our particular cubic equation, we have drawn from the utilitarian online summary provided by Eric Schechter at Vanderbilt University. For a cubic equation of the general form, <math>~ay^3 + by^2 + cy + d = 0 \, ,</math> a real root is given by the expression, <math>~ y = p + \{q + [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} + \{q - [q^2 + (r-p^2)^3]^{1/2}\}^{1/3} \, ,</math> where, <math>~p \equiv -\frac{b}{3a} \, ,</math>      <math>~q \equiv \biggl[p^3 + \frac{bc-3ad}{6a^2} \biggr] \, ,</math>      and      <math>~r=\frac{c}{3a} \, .</math> In our particular case, <math>~a =(1-\kappa_i)\, ,</math>      <math>~b =-3\, ,</math>      <math>~c = 3(1-\kappa_i) \, ,</math>      and      <math>~d = - 3 \, .</math> Hence, <math>~p = \frac{1}{(1-\kappa_i)} \, ,</math>      <math>~r=+1 \, ,</math>      and      <math>~q = p^3 = \frac{1}{(1-\kappa_i)^3} \, ,</math> which implies that the real root, <math>~y_\mathrm{root}</math>, is given by the expression, <math>~(1-\kappa_i)y_\mathrm{root}</math> <math>~=</math> <math>~ 1 + \{1 + [1 + \kappa_i^3(\kappa_i-2)^3 ]^{1/2} \}^{1/3} + \{1 - [1 + \kappa_i^3(\kappa_i-2)^3 ]^{1/2} \}^{1/3} \, . </math> (There is also a pair of imaginary roots, but they are irrelevant in the context of our overarching astrophysical discussion.)

In summary, then,

• Once the ratio, <math>~\mu_e/\mu_c</math>, has been chosen and the location, <math>~\xi_i</math>, of the outer edge of the core has been specified, which determines <math>~\theta_i</math> and <math>~\theta^'_i</math> as well, the value of the parameter, <math>~\kappa_i</math> is known via the expression,

<math>~\kappa_i = - \frac{2\theta_i^' \xi_i}{3\theta_i} \biggl( \frac{\mu_e}{\mu_c} \biggr) \, .</math>

• The value of <math>~y_\mathrm{root}</math> is determined from the just-derived solution to the governing cubic equation, which then gives the interface value of the envelope parameter (adjusted by a <math>~2\pi m</math> phase angle, where <math>~m</math> is an, as yet unspecified, integer),

<math>~\Delta_i = \tan^{-1}(y_\mathrm{root}) \pm 2\pi m \, .</math>

Second Constraint

Now, our 3^rd interface condition, as detailed above, states that,

<math>~\frac{\eta_i}{\xi_i}</math>	<math>~=</math>	<math>~3^{-1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr) \phi_i^{-2}</math>
	<math>~=</math>	<math>~3^{-1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[ \frac{\eta^{1/2} (3-2\sin^2\Delta_i)^{1/2}}{B\sin\Delta_i} \biggr]^{2} </math>
<math>~\Rightarrow ~~~~ B^2</math>	<math>~=</math>	<math>~\frac{\xi_i}{\sqrt{3}} \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[ \frac{(3-2\sin^2\Delta_i)}{\sin^2\Delta_i} \biggr] </math>
<math>~\Rightarrow ~~~~ B</math>	<math>~=</math>	<math>~\biggl[ \frac{\xi_i}{\sqrt{3}} \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl( \frac{3}{\sin^2\Delta_i} - 2\biggr) \biggr]^{1/2} </math>
	<math>~=</math>	<math>~\biggl[ \frac{\xi_i}{\sqrt{3}} \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl( 1 + \frac{3}{y_\mathrm{root}^2}\biggr) \biggr]^{1/2} \, . </math>

Related Discussions

• Polytropes emdeded in an external medium
• Constructing BiPolytropes

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation