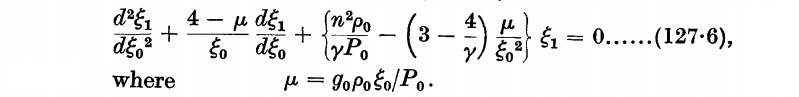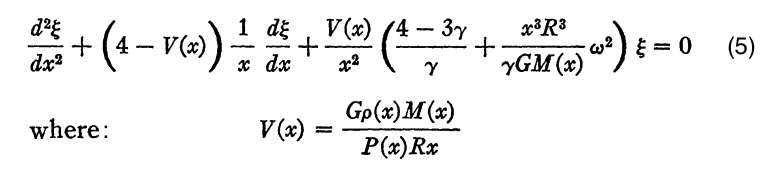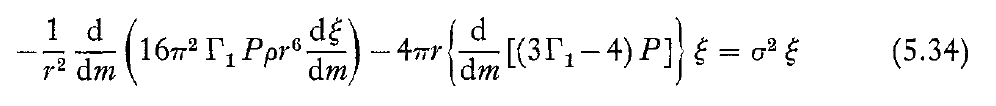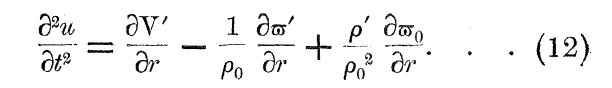Difference between revisions of "User:Tohline/SSC/Perturbations"
(→Spherically Symmetric Configurations (Stability — Part II): MOdify introductory paragraph, pointing to a couple of key reviews) |
(→Spherically Symmetric Configurations (Stability — Part II): Temporarily comment out earliest subsections) |
||
| Line 11: | Line 11: | ||
* An Annual Reviews article titled, [http://adsabs.harvard.edu/abs/1966ARA%26A...4..353C ''Pulsation Theory''] by Christy (1965) and [http://adsabs.harvard.edu/abs/1967IAUS...28....3C Cox (1967)] | * An Annual Reviews article titled, [http://adsabs.harvard.edu/abs/1966ARA%26A...4..353C ''Pulsation Theory''] by Christy (1965) and [http://adsabs.harvard.edu/abs/1967IAUS...28....3C Cox (1967)] | ||
<!-- COMMENT OUT FOR PDF-FORMATTED SUBCHAPTER | |||
==Assembling the Key Relations== | ==Assembling the Key Relations== | ||
| Line 1,024: | Line 1,025: | ||
<math>~x = \biggl( \frac{R}{r_0}\biggr)^{3-4/\gamma_g} \, .</math> | <math>~x = \biggl( \frac{R}{r_0}\biggr)^{3-4/\gamma_g} \, .</math> | ||
</div> | </div> | ||
END COMMENTED-OUT SUBSECTIONS --> | |||
==Classic Papers that Derive & Use this Relation== | ==Classic Papers that Derive & Use this Relation== | ||
Revision as of 23:15, 9 July 2015
Spherically Symmetric Configurations (Stability — Part II)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Suppose we now want to study the stability of one of the spherically symmetric, equilibrium structures that have been derived elsewhere. The identified set of simplified, time-dependent governing equations will tell us how the configuration will respond to an applied radial (i.e., spherically symmetric) perturbation that pushes the configuration slightly away from its initial equilibrium state.
Very useful reviews of this topic include:
- A book titled, The Pulsation Theory of Variable Stars, by S. Rosseland, 1969 (New York: Dover Publications, Inc.) … first published at the Clarendon Press, Oxford, in 1949.
- An Annual Reviews article titled, Pulsation Theory by Christy (1965) and Cox (1967)
Classic Papers that Derive & Use this Relation
Eddington (1926)
To our knowledge, a derivation of this governing 2nd-order ODE was first presented by A. S. Eddington (1926) in a book titled, The Internal Constitution of the Stars. (This entire book has been digitally scanned and is now available online.) The derived expression, which appears on p. 188 as equation (127.6) of Eddington's book, is presented in the following, framed image.
| Pulsation equation extracted† from p. 188 of A. S. Eddington (1926) "The Internal Constitution of the Stars"(Cambridge: Cambridge University Press) |
|---|
| †Mathematical expressions have been displayed here, as a single digital image, with a layout that is modified from the original publication. |
The similarity between Eddington's expression and the governing 2nd-order ODE that we have derived is immediately apparent. Specifically, simply after inserting Eddington's definition of his composite variable, <math>~\mu</math>, and making the substitutions,
<math>~\xi_1 \rightarrow x \, ,</math> <math>\xi_0 \rightarrow r_0 \, ,</math> and <math>n^2 \rightarrow \omega^2 \, ,</math>
Eddington's pulsation equation becomes,
|
<math>~ \frac{d^2 x}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr] \frac{dx}{dr_0} + \frac{\rho_0}{\gamma P_0} \biggl\{\omega^2 + \biggl(4 - 3\gamma\biggr) \frac{g_0 }{r_0} \biggr\}x </math> |
<math>~=</math> |
<math>~0 \, ,</math> |
which exactly matches our derived governing relation.
Ledoux and Pekeris (1941)
Historically, by the 1940s, the expression just derived was a relatively familiar one to astrophysicists. For example, the opening paragraph of a 1941 paper by Ledoux & Pekeris (1941, ApJ, 94, 124), reads:
|
Paragraph extracted from P. Ledoux & C. L. Pekeris (1941)
"Radial Pulsations of Stars"
ApJ, vol. 94, pp. 124-135 © American Astronomical Society |
If we divide their equation (1) through by <math>~Xr = \Gamma_1 P r</math> and recognize that,
<math> \frac{dX}{dr} = \frac{dX}{dm}\frac{dm}{dr} = - \Gamma_1 g_0 \rho \, , </math>
we obtain,
<math> \frac{d^2\xi}{dr^2} + \biggl[ \frac{4}{r} - \frac{g_0 \rho}{P} \biggr] \frac{d\xi}{dr} +\frac{\rho}{\Gamma_1 P} \biggl[ \sigma^2 + (4 - 3\Gamma_1) \frac{g_0}{r} \biggr] \xi = 0 \, . </math>
This is clearly the same <math>2^\mathrm{nd}</math>-order, ordinary differential equation as the one we have derived, but with a more general definition of the adiabatic exponent that allows consideration of a situation where the total pressure is a sum of both gas and radiation pressure.
Schwarzschild (1941)
In the same volume of The Astrophysical Journal, Schwarzschild (1941) published work on "Overtone Pulsations for the Standard [Stellar] Model." The following excerpt has been drawn from the first page of this article.
|
Paragraph extracted from M. Schwarzschild (1941)
"Overtone Pulsations for the Standard Model"
ApJ, vol. 94, pp. 245 - 252 © American Astronomical Society |
|
3A. S. Eddington (1930), The Internal Constitution of the Stars, pp. 188 and 192. |
The similarity between Schwarzschild's "pulsation equation" and the governing 2nd-order ODE that we have derived is immediately apparent; for example, the eigenfrequency, <math>~\omega</math>, is the same in both,
<math>~\xi_1 \leftrightarrow x</math> and <math>\xi_0 \leftrightarrow r_0 \, .</math>
But the two equations are not exactly the same. To show this, we begin by comparing the last term on the lefthand-side in both expressions and presume that Schwarzschild's <math>~u</math> is related to the state variables in our equation as,
<math>u = \frac{\gamma_g P_0}{\rho_0} \, .</math>
Restricting the discussion to only polytropic equations of state — that is, <math>~P_0 = K\rho_0^{(n+1)/n}</math> — we can write,
|
<math>~u</math> |
<math>~=</math> |
<math>~\gamma_g K\rho_0^{1/n} \, ,</math> |
which means that,
|
<math>~\frac{du}{d\xi_0}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\gamma_g K}{n} \biggr) \rho_0^{(1-n)/n} \frac{d\rho_0}{d\xi_0} = \biggl( \frac{\gamma_g}{n+1} \biggr) \frac{1}{\rho_0} \frac{dP_0}{d\xi_0} = - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 \, ,</math> |
where the last step results from recalling that, by our definition above, the unperturbed gravitational acceleration is,
<math>g_0 = - \frac{1}{\rho_0} \frac{dP_0}{dr_0} \, .</math>
Hence, when considering polytropic configurations, the following substitutions are appropriate between the two equations:
<math>\frac{du}{d\xi_0} \leftrightarrow - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 </math> and <math>\frac{1}{u} \frac{du}{d\xi_0} \leftrightarrow - \frac{1}{(n+1)} \frac{g_0 \rho_0}{P_0} \, .</math>
Making these substitutions into Schwarzschild's pulsation equation gives,
|
<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{4}{(n+1)}\biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 - \biggl( \frac{4a\gamma_g}{n+1} \biggr)\frac{g_0}{r_0} \biggr] x = 0 \, . </math> |
Appreciating that, in Schwarzschild's expression, <math>~a \equiv - (4-3\gamma_g)/\gamma_g</math>, we see that our expression matches his if and only if <math>~n=3</math>. This is, indeed, precisely the "standard model" that Schwarzschild was considering.
Review Article by Christy (1966)
In the review by R. F. Christy (1966) titled, Pulsation Theory, this key 2nd-order ODE appears as equation (5) in the form shown by the following boxed-in (slightly edited) excerpt:
|
Pulsation Equation extracted† from R. F. Christy (1966)
"Pulsation Theory"
Annual Review of Astronomy & Astrophysics®, vol. 4, pp. 353 - 392 © Annual Reviews |
|---|
|
†Mathematical expressions displayed here, as a single digital image, with presentation order & layout modified from the original publication.
®Copyright 2015 Annual Reviews. All rights reserved. The Annual Reviews logo, and other Annual Reviews products referenced herein are either registered trademarks or trademarks of Annual Reviews. All other marks are the property of their respective owner and/or licensor. |
Correspondence with our derived equation becomes clear by appreciating that Christy's <math>~x \equiv r_0/R</math> and that,
<math>GM(x) = g_0 r_0^2 \, ,</math>
hence,
<math>V(x) \rightarrow \frac{g_0 \rho_0 r_0}{P_0} \, .</math>
Making these substitutions and multiplying Christy's equation through by <math>~R^{-2}</math> gives,
|
<math>~ \frac{d^2\xi}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr]\frac{d\xi}{dr_0} + \frac{\rho_0}{\gamma_g P_0 } \biggl[(4-3\gamma_g)\frac{g_0}{r_0} + \omega^2 \biggr] \xi </math> |
<math>~=</math> |
<math>~ 0\, . </math> |
Review Article by Cox (1974)
In an excellent review of "Pulsating Stars", J. P. Cox (1974, Reports on Progress in Physics, 37, 563) presents a full derivation of, what he refers to as, the adiabatic wave equation. It appears as equation (5.34) in the form displayed in the following boxed-in image:
|
Adiabatic Wave Equation extracted† from J. P. Cox (1974)
"Pulsating Stars"
Reports on Progress in Physics, vol. 37, pp. 563 - 698 © IOP Publishing |
|---|
| †Equation displayed here, as a single digital image, exactly as it appears in the original publication. |
Recognizing the correspondence with our derived expression requires, first, switching the independent variable from <math>~m</math> to <math>~r_0</math> via the relation identified, above, namely,
|
<math>~ \frac{d}{dm} </math> |
<math>~=</math> |
<math>~ \frac{1}{4\pi \rho_0 r_0^2} \cdot \frac{d}{dr_0} \, , </math> |
to obtain,
|
<math>~ \sigma^2 \xi </math> |
<math>~=</math> |
<math>~ - \frac{1}{(4\pi \rho_0 r_0^4)}\frac{d}{dr_0}\biggl[ (4\pi \Gamma_1 P_0 r_0^4) \frac{d\xi}{dr_0} \biggr] - \frac{1}{\rho_0 r_0} \biggl\{ \frac{d}{dr_0} [ (3\Gamma_1-4)P_0] \biggr\} \xi </math> |
|
|
<math>~=</math> |
<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\frac{d^2 \xi}{dr_0^2} - \frac{\Gamma_1 }{(\rho_0 r_0^4)} \biggl[4P_0 r_0^3 + r_0^4\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} + \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \xi </math> |
|
<math>~\Rightarrow ~~~~ 0</math> |
<math>~=</math> |
<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\biggl\{ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} + \frac{1}{P_0}\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} \biggr\} - \biggl\{ \sigma^2 - \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \biggr\} \xi \, . </math> |
Then, using the definition of <math>~g_0</math>, also as provided above, to facilitate the substitution,
<math>~\frac{dP_0}{dr_0} \rightarrow - g_0 \rho_0 \, ,</math>
gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{g_0 \rho_0}{P_0}\biggr] \frac{d\xi}{dr_0} + \frac{\rho_0 }{\Gamma_1 P_0 }\biggl\{ \sigma^2 + \frac{(4-3\Gamma_1)g_0}{r_0} \biggr\} \xi \, , </math> |
which, apart from the adoption of different variable names, exactly matches our derived expression.
Bonnor (1957)
In a paper titled, "Jeans' Formula for Gravitational Instability," Bonnor (1957, MNRAS, 117, 104) carried out a linear perturbation analysis, preferring to examine the development of Eulerian fluctuations in the matter density rather than the development of Lagrangian position displacements. Here we show the relationship between his approach to a perturbation analysis and the one that we have focused on, above.
Linearized Equations on a Static Background
First, we examine how Bonnor's (1957) linearized Euler equation (2.7) was derived from the nonlinear Euler equation, numbered (2.1) in his paper.
|
Bonnor's (1957, MNRAS, 117, 104) Derivation |
||
|---|---|---|
|
Original nonlinear Euler Equation |
<math>~\rightarrow</math> |
Linearized Euler Equation |
As has been made clear in our introductory discussions, the
Eulerian Representation
of the Euler Equation,
<math>~\frac{\partial\vec{v}}{\partial t} + (\vec{v}\cdot \nabla) \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \Phi</math>
can be counted among the principal set of equations that govern the dynamics of self-gravitating fluids. Accepting that he uses the boldface variable <math>~\mathbf{u}</math> instead of <math>~\vec{v}</math> to represent the fluid velocity, we see that the lefthand side of Bonnor's equation (2.1) exactly matches the lefthand side of the Euler equation, as we have presented it. The term on the righthand side of Bonnor's equation (2.1) that involves a gradient in the gas pressure also matches ours. What remains is to recognize that, in Bonnor's paper,
|
<math>~\mathbf{F}</math> |
<math>~=</math> |
<math>~- \nabla\Phi \, .</math> |
This is confirmed by Bonnor's equation (2.6), which presents another one of our identified set of principal governing equations, namely the
in terms of the vector, <math>~\mathbf{F}</math>, specifically,
|
<math>~\nabla\cdot\mathbf{F}</math> |
<math>~= - \nabla^2\Phi =</math> |
<math>~-4\pi G \rho \, .</math> |
As we have done in our development of the eigenvalue problem, Bonnor (1957) began the process of linearizing the Euler equation by writing each physical variable in terms of its initial, unperturbed value (denoted by subscript "0") plus a "small quantity." For example, he wrote,
|
<math>~\mathbf{u}</math> |
<math>~=</math> |
<math>~\mathbf{u}_0 + \mathbf{u} \, ,</math> |
|
<math>~\mathbf{F}</math> |
<math>~=</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 </math> … and we, furthermore, will write … <math>~\mathbf{F}_0 = -\nabla \Phi_0</math> and <math>~\mathbf{F}_1 = - \nabla \Phi_1 \, ,</math> |
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0 + w \, ,</math> |
|
<math>~\rho</math> |
<math>~=</math> |
<math>~P_0 + q \, .</math> |
[For future reference, notice that the perturbation variable names that we introduced for density and pressure — see above — are different from the ones used by Bonner. They are related via the expressions, <math>(\rho_0 d e^{i\omega t}) \leftrightarrow w</math> and <math>(P_0 p e^{i\omega t}) \leftrightarrow q</math>.] He also initially assumed, as have we, that the unperturbed system is in hydrostatic balance, so,
|
<math>~\mathbf{u}_0</math> |
<math>~=</math> |
<math>~0 \, ,</math> |
|
<math>~\mathbf{F}_0</math> |
<math>~=</math> |
<math>~\frac{1}{\rho_0} \nabla P_0 \, .</math> |
Notice that — confusion notwithstanding — Bonnor did not affix a subscript to the variable being used to represent the velocity perturbation, at least not initially. So, after setting <math>~\mathbf{u}_0 = 0</math>, the generic velocity vector, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.1) becomes the small in magnitude velocity perturbation, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.7); and, in his equation (2.7), the <math>~(\mathbf{u}\cdot \nabla)\mathbf{u}</math> term disappears altogether because it involves the product of two quantities that are both small in magnitude. Although details of the derivation are not presented in Bonnor's (1957) paper, it is reasonable to assume that he took the following steps in linearizing the righthand side of equation (2.1):
|
RHS of equation (2.1) |
<math>~\rightarrow</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{(\rho_0 + w)} \nabla(P_0 + q) </math> |
|
|
<math>~=</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 + \frac{w}{\rho_0} \biggr)^{-1}\nabla(P_0 + q) </math> |
|
|
<math>~\approx</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 - \frac{w}{\rho_0} \biggr)\nabla(P_0 + q) </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \mathbf{F}_0 - \frac{1}{\rho_0}\nabla P_0 \biggr] + \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla q</math> |
|
|
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 \, .</math> |
As is shown in the following framed image, if the discussion is restricted only to fluctuations in the radial coordinate direction of a spherically symmetric configuration, in which case <math>~\nabla \rightarrow \partial/\partial r</math>, this expression exactly matches the righthand side of the linearized Euler equation, derived and presented as equation (12) by James H. Jeans in 1902 (Philosophical Transactions of the royal Society of London. Series A, 199, 1).
|
Linearized Euler Equation as Derived and Presented by Jeans (1902) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
The correspondence between the righthand-sides of equation (12) from Jeans (1902) and our derived expression [using Bonnor's (1957) variable notation] is clear after accepting the following variable mappings:
The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of Bonnor's (1957) linearized Euler equation, although this may not be immediately apparent because the variable "u" has been assigned different meanings in the two publications. In Bonnor's paper, <math>~u = \hat{\mathbf{e}}_r \cdot \mathbf{u}</math> is the perturbed velocity in the radial-coordinate direction; while, in the paper by Jeans, <math>~u</math> is the radial displacement itself. Hence,
|
Now, in order to morph this last expression into the expression found on the righthand side of Bonnor's equation (2.7), as reprinted above, we need to draw upon the result obtained, above, from linearizing the adiabatic form of the First Law of Thermodynamics. After shifting to Bonnor's variable notation (as clarified in earlier remarks), the relevant result is,
<math>\frac{q}{P_0} \approx \gamma_g \frac{w}{\rho_0} \, .</math>
In addition, we appreciate that,
<math>\gamma_g = \biggl( \frac{d\ln P}{d\ln \rho} \biggr)_0 = \frac{\rho_0}{P_0}\cdot \biggl( \frac{dP}{d\rho} \biggr)_0 \, .</math>
Hence (see also Bonnor's equation 3.7),
<math>q \approx w \biggl( \frac{dP}{d\rho} \biggr)_0 \, ,</math>
which allows us to write the righthand side of the linearized Euler equation as,
|
RHS of equation (2.1) |
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \biggl\{ \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0} \biggr)\nabla P_0\biggr\} \, .</math> |
But, given the adopted barotropic equation of state, we can also write,
<math>\nabla P_0 = \biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0 \, ,</math>
in which case,
|
RHS of equation (2.1) |
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \biggl\{\frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0^2} \biggr)\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \mathbf{F}_1 - \biggl\{ \frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] + w\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\biggl(\frac{1}{\rho_0} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \mathbf{F}_1 - \nabla \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math> |
This precisely matches the righthand side of the linearized Euler equation derived and presented as equation (2.7) by Bonnor — see the reprinted equation, above.
Reconciliation
It is instructive to explicitly demonstrate that the linearized "Euler + Poisson" equation that we derived and highlighted in our brief summary subsection, above, namely,
|
<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x \, , </math> |
conveys the same physics as Bonnor's (1957) linearized Euler equation when applied to a spherically symmetric system, namely,
|
<math>\frac{\partial v_r}{\partial t}</math> |
<math>~=</math> |
<math>~ \hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math> |
Step #1: We recognize that, after linearization, <math>~\partial v_r/\partial t = d^2 r/dt^2</math>. So, drawing on our earlier detailed handling of the "Euler + Poisson" equations, we can make the replacement,
|
<math> \frac{\partial v_r}{\partial t} </math> |
<math> \rightarrow </math> |
<math> - ~\omega^2 r_0 x~e^{i\omega t} \, . </math> |
Step #2: As we have already recognized, swapping between our perturbation notation and Bonnor's leads to the replacement,
|
<math> w \biggl( \frac{dP}{d\rho} \biggr)_0 </math> |
<math> \rightarrow </math> |
<math> P_0 p e^{i\omega t} \, . </math> |
Hence,
|
<math> \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math> |
<math> \rightarrow </math> |
<math> \frac{d}{d r_0} \biggl[ \biggl( \frac{P_0 p}{\rho_0}\biggr) e^{i\omega t} \biggr] </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl\{ \frac{p}{\rho_0} \frac{d P_0}{d r_0} + P_0 p \frac{d}{d r_0} \biggl( \frac{1}{\rho_0}\biggr) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl\{ \biggl[ \frac{1}{\rho_0} \frac{d P_0}{d r_0} \biggr] (p - d) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] \, . </math> |
where we have, again, used the relationship,
|
<math>\nabla P_0 = \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 = \biggl( \frac{P_0 p}{\rho_o d} \biggr) \nabla \rho_0 </math> |
<math>~~~~\Rightarrow~~~~</math> |
<math>~ \frac{d}{dr_0} \biggl( \frac{1}{\rho_0}\biggr) = - \frac{1}{\rho_0^2}\frac{d\rho_0}{dr_0} =- \biggl( \frac{d}{P_0 p} \biggr) \biggl[\frac{1}{\rho_0}\frac{dP_0}{dr_0} \biggr] \, .</math> |
Step #3: Implementing these first two substitutions, Bonnor's linearized Euler equation becomes,
|
<math>- ~\omega^2 r_0 x</math> |
<math>~=</math> |
<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] </math> |
|
<math>\Rightarrow ~~~~ \frac{P_0}{\rho_0} \frac{d p}{d r_0} </math> |
<math>~=</math> |
<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 + (p - d) g_0 + \omega^2 r_0 x\, .</math> |
Step #4: In order to map Bonnor's <math>~\mathbf{F}_1</math> to our perturbation notation, we back up to expressions for the gravitational acceleration, as a whole, which establish that, for spherically symmetric systems,
|
<math>~\hat{\mathbf{e}}_r \cdot \mathbf{F}</math> |
<math>~=</math> |
<math>~-~\frac{Gm}{r^2}</math> |
|
<math>~\Rightarrow~~~\hat{\mathbf{e}}_r \cdot \biggl[ \mathbf{F}_0 + \mathbf{F}_1 \biggr]</math> |
<math>~=</math> |
<math>~-~\frac{Gm}{r^2}</math> |
Dimensionless Expression
Let's write this governing, 2nd-order ODE and the key physical variables as dimensionless expressions. First, multiply through by <math>~R^2</math> and define the dimensionless radius as,
<math>
\chi_0 \equiv \frac{r_0}{R}
</math>
to obtain,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{R g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{R^2 \rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 .
</math>
Now normalize <math>~P_0</math> to <math>~P_c</math> and <math>~\rho_0</math> to <math>~\rho_c</math> to obtain,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R g_0 \rho_c}{P_c}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R^2 \rho_c}{\gamma_\mathrm{g} P_c} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 \, .
</math>
The characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) appears to be,
<math>
\tau_\mathrm{SSC} \equiv \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} ,
</math>
and the characteristic gravitational acceleration appears to be,
<math>
g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} .
</math>
So we can write,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 .
</math>
This is the governing relation that we will use to analyze the stability against radial pulsations of spherically symmetric, self-gravitating configurations.
Complementary Approach
Looking back at the set of three, coupled, linearized equations — but using <math>~\Delta</math> to denote the density fluctuation, rather than <math>~d</math>, in order to avoid confusion with the differentiation operators,
|
Linearized Linearized Linearized |
let's combine them into a 2nd-order ODE that governs the eigenfunction of the density perturbation, <math>~\Delta</math>, rather than of the radial displacement, <math>~x</math>. We begin by using the second equation to obtain an expression for <math>~x</math>:
|
<math>~ x</math> |
<math>~=</math> |
<math>~(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \, .</math> |
From this, we determine that,
|
<math>~ (4g_0 + \omega^2 r_0)\frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] + (4g_0 + \omega^2 r_0)\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0}(4g_0 + \omega^2 r_0)^{-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \cdot \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) -p \frac{dg_0}{dr_0} - g_0\frac{dp}{dr_0} - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \biggl\{ -g_0 + \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] \biggr\} + p \biggl\{ (4g_0 + \omega^2 r_0)^{-1}\biggl[ g_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] -\frac{dg_0}{dr_0} \biggr\} </math> |
Next, we substitute this expression for <math>~x</math> into the first equation — gradually replacing <math>~p</math> with <math>~\gamma_g \Delta</math>, as well — and carry out the differentiation:
|
<math>~ -\Delta - 3\biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - \gamma_g \Delta g_0 \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~r_0 \frac{d}{dr_0} \biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggr\} </math> |
|
<math>~ \Rightarrow~~- \Delta \biggl[ \frac{g_0}{r_0} (4 - 3\gamma_g)+ \omega^2 \biggr] - \frac{3P_0}{r_0 \rho_0} \frac{dp}{dr_0} </math> |
<math>~=</math> |
<math>~ \frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] - (4g_0 + \omega^2 r_0)^{-1} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0} \biggl[(4g_0 + \omega^2 r_0) \biggr] </math> |
See Also
- The History of Radial Stellar Pulsation Theory by A. Gautschy (2003)
- Part I of Spherically Symmetric Configurations: Simplified Governing Equations
- Wave Equation
- Sound Waves and Gravitational Instability — class notes provided online by David H. Weinberg (The Ohio State University)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |