Difference between revisions of "User:Tohline/SSC/FreeEnergy/PowerPoint"
(→Case M: Insert Figure 1, which illustrates the Case M equilibrium sequence for n=5) |
|||
| Line 235: | Line 235: | ||
=====Virial Equilibrium===== | =====Virial Equilibrium===== | ||
<table align="right" border="0" cellpadding="5" width="360px"> | |||
<tr><th align="center"><font size="+1">Figure 1</font></th></tr> | |||
<tr><td align="center"> | |||
[[File:PvsR_simplest.png|350px|Simplest Case M sequence]] | |||
</td></tr></table> | |||
So the statement of virial equilibrium becomes, | So the statement of virial equilibrium becomes, | ||
<div align="center"> | <div align="center"> | ||
| Line 293: | Line 298: | ||
</table> | </table> | ||
</div> | </div> | ||
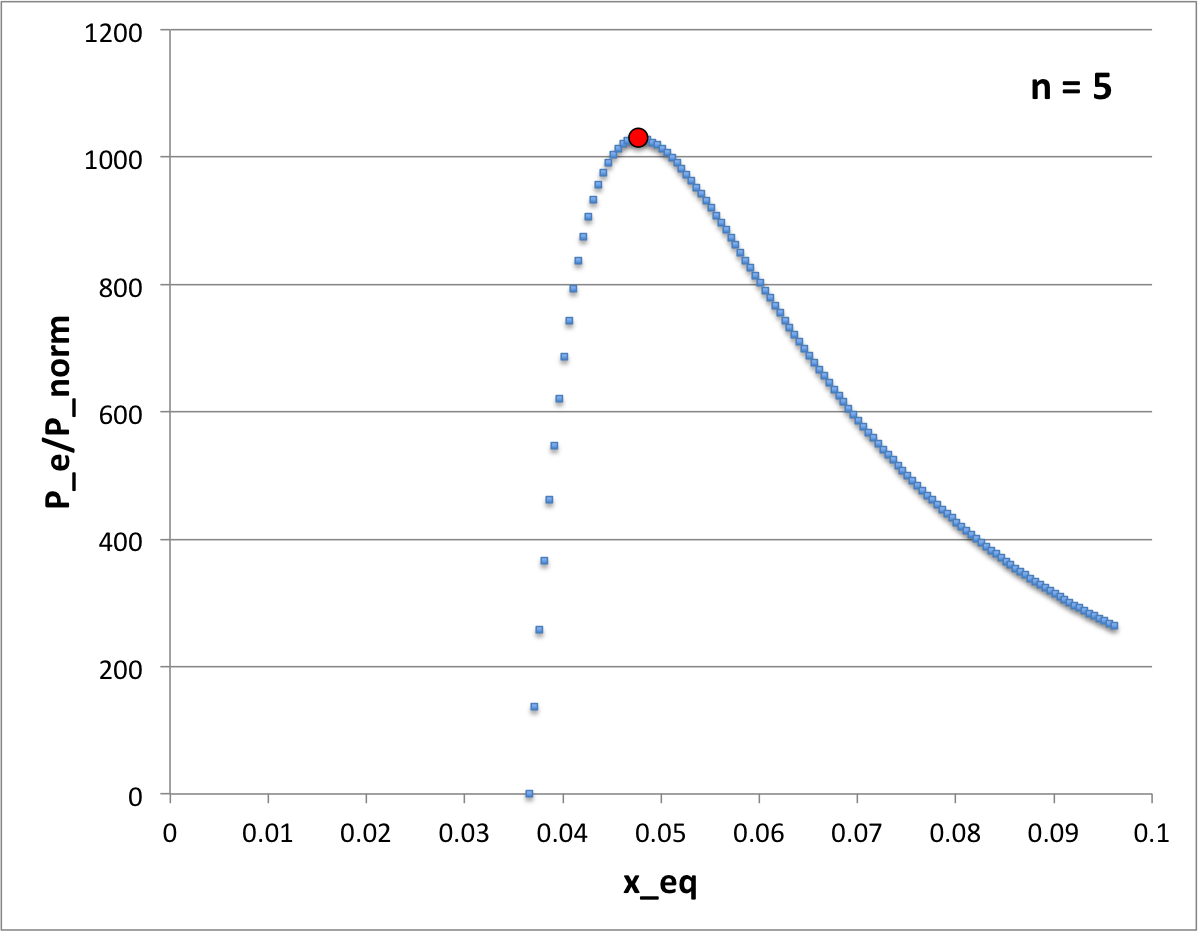
The light-blue dots in Figure 1 trace the equilibrium sequence that is defined by this virial equilibrium function in the case of <math>~n = 5</math>. | |||
=====Dynamical Instability===== | =====Dynamical Instability===== | ||
Along this equilibrium sequence, the transition from stable to unstable configurations occurs at, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 361: | Line 368: | ||
</table> | </table> | ||
</div> | </div> | ||
The location of this critical configuration along the <math>~n=5</math> equilibrium sequence is marked by the red circular dot in Figure 1. | |||
=====Turning Point===== | =====Turning Point===== | ||
| Line 505: | Line 514: | ||
</div> | </div> | ||
Notice that, under the assumption that all three structural filling-factors are unity, <math>~[x_\mathrm{eq}]_\mathrm{turn} = [x_\mathrm{eq}]_\mathrm{crit}</math>, that is, the location of the turning point coincides precisely with the point along the sequence where the transition from stable to unstable equilibrium configurations occurs. | Notice that, under the assumption that all three structural filling-factors are unity, <math>~[x_\mathrm{eq}]_\mathrm{turn} = [x_\mathrm{eq}]_\mathrm{crit}</math>, that is, the location of the turning point coincides precisely with the point along the equilibrium sequence where the transition from stable to unstable equilibrium configurations occurs (marked by the red circular dot in Figure 1). | ||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 20:03, 19 August 2016
Supporting Derivations for Free-Energy PowerPoint Presentation
The derivations presented here are an extension of our accompanying free-energy synopsis. These additional details proved to be helpful while developing an overarching PowerPoint presentation.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
General Free-Energy Expression
We're considering a free-energy function of the following form:
|
<math>~\mathfrak{G}^*_\mathrm{type}</math> |
<math>~=</math> |
<math>~-ax^{-1} + b x^{-3/n} + c x^{-3/j} + \mathfrak{G}_0 \, ,</math> |
where,
<math>~x \equiv \frac{R}{R_0} \, .</math>
As we have shown, setting,
|
<math>~\frac{\partial \mathfrak{G}^*_\mathrm{type}}{\partial x}</math> |
<math>~=</math> |
<math>~0 \, ,</math> |
generates a mathematical statement of virial equilibrium, namely,
|
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} + \frac{1}{j}\cdot x^{(j-3)/j}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ 0 \, .</math> |
And equilibrium configurations for which the second (as well as first) derivative of the free energy is zero are found at "critical" radii given by the expression,
|
<math>~[x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \frac{a}{3^2c}\biggl[ \frac{j^2(n-3)}{n-j} \biggr] \, . </math> |
Pressure-Truncated Polytropes
For pressure-truncated polytropes, set <math>~j=-1</math> and let <math>~n</math> be the chosen polytropic index. In this case, the statement of virial equilibrium is,
|
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ 0 \, ;</math> |
and the critical equilibrium configuration has,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{a(n-3)}{3^2c (n+1)}\biggr]^{1/4} \, . </math> |
Case M
Set <math>~K</math> and <math>~M_\mathrm{tot}</math> constant and examine how the free-energy behaves as a function of the coordinates, <math>~(R,P_e)</math>. In this case (see, for example, here),
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, , </math> |
where the structural form factors for pressure-truncated polytropes are precisely defined here. And (see, for example, here),
|
<math>~R_0 = R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, .</math> |
If we set all three structural form-factors to unity, we have,
|
<math>~\frac{a}{3c}</math> |
<math>~=</math> |
<math>~\frac{3}{2^2\cdot 5\pi}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, ,</math> |
|
<math>~\frac{b}{nc}</math> |
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, .</math> |
Virial Equilibrium
| Figure 1 |
|---|
So the statement of virial equilibrium becomes,
|
<math>~ x^{4}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~\biggl[ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{2^2\cdot 5\pi}\biggr]\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{2^2\cdot 5\pi}\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{eq} - 1\biggr]\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math> |
|
<math>~ \Rightarrow ~~~ \frac{P_e}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{3}{2^2\cdot 5\pi x^{4}_\mathrm{eq} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{eq} - 1\biggr] \, . </math> |
The light-blue dots in Figure 1 trace the equilibrium sequence that is defined by this virial equilibrium function in the case of <math>~n = 5</math>.
Dynamical Instability
Along this equilibrium sequence, the transition from stable to unstable configurations occurs at,
|
<math>~[x_\mathrm{eq}]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] \frac{3}{2^2\cdot 5\pi}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math> |
|
<math>~\Rightarrow ~~~ \frac{2^2\cdot 5\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)[x_\mathrm{eq}]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] </math> |
which, in combination with the virial equilibrium condition gives,
|
<math>~5\biggl(\frac{3}{4\pi} \biggr)^{1/n} [x_\mathrm{eq}]^{(n-3)/n }_\mathrm{crit} -1</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{4n}{3\cdot 5(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n}\biggr]^{n/(n-3)} \, . </math> |
The location of this critical configuration along the <math>~n=5</math> equilibrium sequence is marked by the red circular dot in Figure 1.
Turning Point
Let's examine the curvature of the equilibrium sequence.
|
<math>~ \frac{d}{dx}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)</math> |
<math>~=</math> |
<math>~ - \frac{3}{ 5\pi x^{5} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n } - 1\biggr] + \frac{3(n-3)}{2^2n \pi x^{4} }\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{-3/n } </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{ 5\pi x^{5} } + \frac{3}{4\pi}\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggl[ \frac{(n-3)}{n } - 4\biggr] \frac{x^{(n-3)/n } }{x^5} </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{ 5\pi x^{5} } - 3\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \biggl[ \frac{n+1}{n } \biggr] \frac{x^{(n-3)/n } }{x^5} \, . </math> |
Setting this derivative to zero let's us identify the location of the turning point that identifies <math>~P_\mathrm{max}.</math>
|
<math>~ [ x_\mathrm{eq}^{(n-3)/n } ]_\mathrm{turn} </math> |
<math>~=</math> |
<math>~ \frac{1}{ 5\pi }\biggl[ \frac{n }{n+1} \biggr] \biggl(\frac{4\pi}{3} \biggr)^{(n+1)/n} </math> |
|
<math>~\Rightarrow~~~ [ x_\mathrm{eq} ]_\mathrm{turn} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{4n}{ 15(n+1)}\biggl(\frac{4\pi}{3} \biggr)^{1/n} \biggr]^{n/(n-3)} \, . </math> |
And, returning to the virial equilibrium expression, we find that, associated with this equilibrium radius,
|
<math>~ \frac{P_\mathrm{max}}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{3}{2^2\cdot 5\pi x^{4}_\mathrm{turn} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{turn} - 1\biggr] </math> |
|
<math>~ \Rightarrow ~~~2^2\cdot 5\pi x^{4}_\mathrm{turn} \biggl(\frac{P_\mathrm{max}}{P_\mathrm{norm}}\biggr)</math> |
<math>~=</math> |
<math>~15\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggl[ \frac{4n}{ 15(n+1)}\biggl(\frac{4\pi}{3} \biggr)^{1/n} \biggr] - 3 </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{n-3}{ n+1} \biggr) </math> |
|
<math>~ \Rightarrow ~~~\frac{P_\mathrm{max}}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{1}{20\pi}\biggl(\frac{n-3}{ n+1} \biggr) \biggl[ \frac{ 15(n+1)}{4n}\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggr]^{4n/(n-3)} \, .</math> |
Notice that, under the assumption that all three structural filling-factors are unity, <math>~[x_\mathrm{eq}]_\mathrm{turn} = [x_\mathrm{eq}]_\mathrm{crit}</math>, that is, the location of the turning point coincides precisely with the point along the equilibrium sequence where the transition from stable to unstable equilibrium configurations occurs (marked by the red circular dot in Figure 1).

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |