User:Tohline/AxisymmetricConfigurations/PoissonEq

Solving the Poisson Equation Numerically

The set of Principal Governing Equations that serve as the foundation of our study of the structure, stability, and dynamical evolution of self-gravitating fluids contains an equation of motion (the Euler equation) that includes an acceleration due to local gradients in the (Newtonian) gravitational potential, <math>~\Phi</math>. As has been pointed out in an accompanying chapter that discusses the origin of the Poisson equation, the mathematical definition of this acceleration is fundamentally drawn from Isaac Newton's inverse-square law of gravitation, but takes into account that our fluid systems are not point-mass sources but, rather, are represented by a continuous distribution of mass via the function, <math>~\rho(\vec{x},t)</math>. As indicated, in our study, <math>~\rho</math> may depend on time as well as space. The acceleration felt at any point in space is obtained by integrating over the accelerations exerted by each differential mass element. As has been explicitly demonstrated in, respectively, Step 1 and Step 3 of the same accompanying chapter, at any point in time the spatial variation of the gravitational potential, <math>~\Phi(\vec{x})</math>, may be determined from <math>~\rho(\vec{x})</math> via either an integral or a differential equation as follows:

Poisson Equation
Integral Expression	Differential Expression
<math>~ \Phi(\vec{x})</math> <math>~=</math> <math>~ -G \int \frac{\rho(\vec{x}^{~'})}{|\vec{x}^{~'} - \vec{x}|} d^3x^' \, .</math>	<math>\nabla^2 \Phi = 4\pi G \rho</math>

While it is possible in some restricted situations to determine analytic expressions for the matched pair of functions, <math>~\Phi </math> and <math>~\rho</math>, that satisfy the Poisson equation, modeling the vast majority of interesting astrophysical problems requires the develop of a numerical scheme to solve the Poisson equation. In what follows, our aim is twofold: (a) To recount — in a reasonable amount of detail — the steps that we have taken over the past, approximately forty years to develop more and more accurate and efficient ways to solve the Poisson equation in full three-dimensional generality; and (b) To list, if not summarize, alternative techniques that have been successfully employed by other research groups over the years.

Our Approach

Influenced by Black & Bodenheimer (1975)

D. C. Black & P. Bodenheimer (1975, ApJ, 199, 619 - 632) published a detailed description of the numerical techniques that they implemented in order to model, in two dimensions, the dynamical collapse of axisymmetric interstellar gas clouds. Among the techniques was their method of solving, in cylindrical coordinates, the two-dimensional (2D) Poisson equation. As is acknowledged in the last paragraph of their paper, Black & Bodenheimer were introduced "to the pitfalls of two-dimensional hydrodynamics" by Drs. J. LeBlanc and J. Wilson who, at the time, were both staff scientists at the Lawrence Livermore Laboratory. In 1976, having completed my formal graduate-level course work in the astronomy program at UC, Santa Cruz, Peter Bodenheimer (on the faculty of Lick Observatory and UC, Santa Cruz) asked me if I would be interested in working with him and David Black (a planetary scientist at NASA, Ames Research Center) on the development of a fully three-dimensional hydrodynamics code to study, not only the collapse, but also the fragmentation of self-gravitating gas clouds. I jumped at the opportunity. As a result, an effort to model the process of spontaneous cloud fragmentation became the focus of my doctoral dissertation research.

Borrowing from the Black & Bodenheimer (1975) work, I decided to solve the set of 3D principal governing equations on a cylindrical coordinate <math>~(R, \theta, Z)</math> mesh:

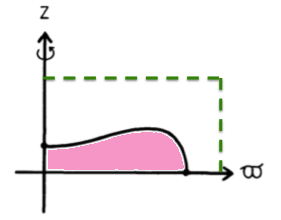
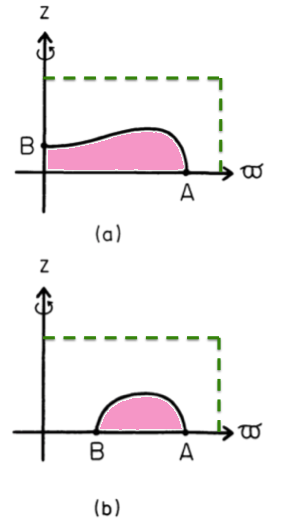
• whose outermost radial and vertical boundaries were placed entirely outside of the mass distribution (by way of illustration, see the green-dashed lines in the annotated figure, below);
• that exhibited reflection symmetry through the <math>~(Z = 0)</math> equatorial plane ;
• that allowed for non-uniform (logarithmically stretched) grid spacing in both the radial and vertical directions; and,
• (extending the Black & Bodenheimer work from 2D to 3D) with strictly uniform spacing in the azimuthal-coordinate direction.

---

Mesh Choice: In retrospect, I am still comfortable with the choice of a cylindrical coordinate mesh with uniform spacing in the azimuthal-coordinate direction. When expressed in terms of cylindrical coordinates — as opposed to cartesian coordinates, for example — the azimuthal component of the Euler equation offers a natural means by which the conservation of angular momentum can be monitored, if not enforced. And, by enabling the implementation of FFTs — hence, providing the ability to rapidly transform functions, like <math>~\Phi(\theta)</math> and <math>~\rho(\theta)</math>, back and forth between real space and Fourier space — a uniform descritization of the azimuthal grid facilitates the development of an efficient 3D Poisson solver as well as tools to straightforwardly analyze the behavior — e.g., the exponential growth — of individual nonaxisymmetric modes.

---

Also, following the lead of Black & Bodenheimer (1975), a hybrid scheme was developed to solve the Poisson equation. As defined immediately above, the integral expression was evaluated at grid locations along the outermost radial and vertical boundaries — illustrated by the dashed green lines displayed in the figure, here on the right — by integrating over the "pink" mass distribution lying inside of these grid boundaries. Separately, the differential expression was used to evaluate the potential at all interior grid locations; this differential expression was supplemented by the implementation of Neumann boundary conditions (reflection symmetry) along the equatorial plane, and by using the values of the potential just determined along the outermost grid boundaries to provide Direchlet boundary conditions along those gird boundaries.

Determining Values of the Potential on the Mesh Boundary

Relevant Green's Functions
In terms of <math>~P_\ell^m(\cos\theta)</math> (Associated Legendre Functions)	Leading Legendre Functions	Leading Spherical Harmonics
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'} |}</math> <math>~=</math> <math>~\sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{4\pi}{2\ell+1} \biggl[ \frac{r_<^\ell}{r_>^{\ell+1}} \biggr] Y_{\ell m}^*(\theta^', \phi^') Y_{\ell m}(\theta,\phi)</math> where: <math>~Y_{\ell m}(\theta,\phi) = \biggl[ \frac{(2\ell + 1 )(\ell - m)!}{4\pi(\ell + m)!} \biggr]^{1 / 2} P_\ell^m(\cos\theta)e^{im\phi}</math> J. D. Jackson (1975, 2nd Edition), Eqs. (3.70), (3.53), (3.49) & (3.16)	<math>~P_0(x)</math> <math>~=</math> <math>~1</math> <math>~P_1(x)</math> <math>~=</math> <math>~x</math> <math>~P_2(x)</math> <math>~=</math> <math>~\tfrac{1}{2}(3x^2 - 1)</math> <math>~P_3(x)</math> <math>~=</math> <math>~\tfrac{1}{2}(5x^3 - 3x)</math> <math>~P_4(x)</math> <math>~=</math> <math>~\tfrac{1}{8}(35x^4 - 30x^2 + 3)</math> <math>~P_5(x)</math> <math>~=</math> <math>~\tfrac{1}{8}(63x^5 - 70x^3 + 15x)</math> <math>~P_6(x)</math> <math>~=</math> <math>~\tfrac{1}{16}(231x^6 - 315x^4 + 105x^2 - 5)</math>
See also the DLMF's: definition of spherical harmonics, <math>~Y_{\ell m}</math>; definition of Associated Legendre Functions, <math>~P_\ell^m(x)</math>; list of the first seven Legendre Functions, <math>~P_\ell(x)</math>

Let's determine the potential, <math>~\Phi_B</math>, at all points along the boundary of the cylindrical coordinate mesh by evaluating the integral representation for the Poisson equation. Let's accomplish this by inserting the Green's function expression for <math>~|\vec{x} - \vec{x}^{~'}|^{-1} </math> as given in terms of Spherical Harmonics, <math>~Y_{\ell m}</math>, and ultimately in terms of Associated Legendre Functions. Written in the context of a spherical coordinate system we have,

<math>~ \Phi_B(r,\theta,\phi)</math>	<math>~=</math>	<math>~ -G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ -G \int \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{4\pi}{2\ell+1} \biggl[ \frac{r_<^\ell}{r_>^{\ell+1}} \biggr] Y_{\ell m}^*(\theta^', \phi^') Y_{\ell m}(\theta,\phi) ~\rho(r^', \theta^', \phi^') d^3x^' </math>
	<math>~=</math>	<math>~ -4\pi G \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)r^{\ell+1}} \int (r^')^\ell Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' \, . </math>

Rewriting this expression in terms of cylindrical coordinates — which aligns with our chosen grid coordinate system — and admitting that in practice our summation over the index, <math>~\ell</math>, cannot extend to infinity, we have,

<math>~ \Phi_B(R, \phi, z)</math>

<math>~=</math>

<math>~ -4\pi G \sum_{\ell=0}^{\ell_\mathrm{max}} \sum_{m=-\ell}^{+\ell} \frac{Y_{\ell m}}{(2\ell+1)} \biggl[ R^2 + z^2 \biggr]^{-(\ell+1)/2} \int Y_{\ell m}^* \biggl[ (R^')^2 + (z^')^2 \biggr]^{\ell/2} ~\rho(R^', \phi^', z^') d^3x^' \, . </math>

Note: As a consequence of assuming that our configurations have equatorial-plane symmetry, the integral over the mass distribution necessarily goes to zero for all odd values of the index, <math>~\ell</math>. After setting <math>~\ell_\mathrm{max}=4</math>, this is the expression that was used to determine the boundary values of the gravitational potential in our earliest set of simulations; for example, Tohline (1978), Tohline (1980), and Bodenheimer, Tohline, & Black (1980).

Relevant Green's Functions
In terms of <math>~P_\ell^m(\cos\theta)</math> (Associated Legendre Functions)	Leading Legendre Functions	In terms of <math>~Q_{m - 1 / 2}(\chi)</math> (Half-Integer Degree Legendre Functions of the 2nd Kind)
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'} |}</math> <math>~=</math> <math>~\sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{4\pi}{2\ell+1} \biggl[ \frac{r_<^\ell}{r_>^{\ell+1}} \biggr] Y_{\ell m}^*(\theta^', \phi^') Y_{\ell m}(\theta,\phi)</math> where: <math>~Y_{\ell m}(\theta,\phi) = \biggl[ \frac{(2\ell + 1 )(\ell - m)!}{4\pi(\ell + m)!} \biggr]^{1 / 2} P_\ell^m(\cos\theta)e^{im\phi}</math> J. D. Jackson (1975, 2nd Edition), Eqs. (3.70), (3.53), (3.49) & (3.16)	<math>~P_0(x)</math> <math>~=</math> <math>~1</math> <math>~P_1(x)</math> <math>~=</math> <math>~x</math> <math>~P_2(x)</math> <math>~=</math> <math>~\tfrac{1}{2}(3x^2 - 1)</math> <math>~P_3(x)</math> <math>~=</math> <math>~\tfrac{1}{2}(5x^3 - 3x)</math> <math>~P_4(x)</math> <math>~=</math> <math>~\tfrac{1}{8}(35x^4 - 30x^2 + 3)</math> <math>~P_5(x)</math> <math>~=</math> <math>~\tfrac{1}{8}(63x^5 - 70x^3 + 15x)</math> <math>~P_6(x)</math> <math>~=</math> <math>~\tfrac{1}{16}(231x^6 - 315x^4 + 105x^2 - 5)</math>	<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> <math>~=</math> <math>~ \frac{1}{\pi \sqrt{RR^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) </math> where: <math>~\chi \equiv \frac{R^2 + (R^')^2 + (z - z^')^2}{2RR^'}</math> H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16)
See also the DLMF's: definition of spherical harmonics, <math>~Y_{\ell m}</math>; definition of Associated Legendre Functions, <math>~P_\ell^m(x)</math>; list of the first seven Legendre Functions, <math>~P_\ell(x)</math>		See also the DLMF's: definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>

Extension from 2D to 3D

An extension from 2D to 3D was accomplished by using separate, finite Fourier series expansion to represent the azimuthal dependence of <math>~\rho</math> and <math>~\Phi</math>. This allowed us to decouple the differential expression for the Poisson equation into a finite number of independent Fourier modes, and to straightforwardly solve a finite set of 2D Helmholtz equations, instead of solving a single 2D Poisson equation.

Constructing Two-Dimensional, Axisymmetric Structures

As has been explained in an accompanying discussion, our objective is to solve an algebraic expression for hydrostatic balance,

<math>~H + \Phi + \Psi = C_0</math> ,

in conjunction with the Poisson equation in a form that is appropriate for two-dimensional, axisymmetric systems, namely,

<math>~ \frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho . </math>

Steps to Follow

Annotation of Figure 1 from I. Hachisu (1986) One quadrant of a meridional-plane cross-section (pink) through: (a) spheroidal structure; (b) toroidal structure. A green, dashed rectangular grid boundary is also illustrated.

1. Choose a particular barotropic equation of state.   More specifically, functionally define the density-enthalpy relationship, <math>~\rho(H)</math>, and identify what value, <math>~H_\mathrm{surface}</math>, the enthalpy will have at the surface of your configuration. For example, if a polytropic equation of state is adopted, <math>~H_\mathrm{surface} = 0</math> is a physically reasonable prescription.
2. Choosing from, for example, a list of astrophysically relevant simple rotation profiles, specify the corresponding functional form of the centrifugal potential, <math>~\Psi(\varpi)</math>, that will define the radial distribution of specific angular momentum in your equilibrium configuration. If the choice is uniform rotation, then <math>~\Psi = - \varpi^2 \omega_0^2/2 \, ,</math> where <math>~\omega_0</math> is a constant to be determined.
3. On your chosen computational lattice — for example, on a cylindrical-coordinate mesh — identify two boundary points, A and B, that will lie on the surface of your equilibrium configuration. These two points should remain fixed in space during the HSCF iteration cycle and ultimately will confine the volume and define the geometry of the derived equilibrium object. Note that, by definition, the enthalpy at these two points is, <math>~H_A = H_B = H_\mathrm{surface}</math>.
4. Throughout the volume of your computational lattice, guess a trial distribution of the mass density, <math>~\rho(\varpi,z)</math>, such that no material falls outside a volume defined by the two boundary points, A and B, that were identified in Step #3. Usually an initially uniform density distribution will suffice to start the SCF iteration.
5. Via some accurate numerical algorithm, solve the Poisson equation to determine the gravitational potential, <math>~\Phi(\varpi,z)</math>, throughout the computational lattice corresponding to the trial mass-density distribution that was specified in Step #4 (or in Step #9).
6. From the gravitational potential determined in Step #5, identify the values of <math>~\Phi_A</math> and <math>~\Phi_B</math> at the two boundary points that were selected in Step #3.
7. From the "known" values of the enthalpy (Step #3) and the gravitational potential (Step #6) at the two selected surface boundary points A and B, determine the values of the constants, <math>~C_0</math> and <math>~\omega_0</math>, that appear in the algebraic equation that defines hydrostatic equilibrium.
8. From the most recently determined values of the gravitational potential, <math>~\Phi(\varpi,z)</math> (Step #5), and the values of the two constants, <math>~C_0</math> and <math>~\omega_0</math> just determined (Step #7), determine the enthalpy distribution throughout the computational lattice.
9. From <math>~H(\varpi,z)</math> and the selected barotropic equation of state (Step #1), calculate an "improved guess" of the density distribution, <math>~\rho(\varpi,z)</math>, throughout the computational lattice.
10. Has the model converged to a satisfactory equilibrium solution? (Usually a satisfactory solution has been achieved when the derived model parameters — for example, the values of <math>~C_0</math> and <math>~\omega_0</math> — change very little between successive iterations and the viral error is sufficiently small.)
    • If the answer is, "NO":   Repeat steps 5 through 10.
    • If the answer is, "YES":   Stop iteration.

Related Discussions

Reviews

• P. A. Strittmatter (1969, Annual Review of Astronomy and Astrophysics, 7, 665 - 684) — Stellar Rotation
• N. R. Lebovitz (1967, Annual Review of Astronomy and Astrophysics, 5, 465 - 480) — Rotating Fluid Masses

Solution Methods

• Y. Eriguchi & E. Mueller (1985, A&A, 146, 260 - 268) — A General Computational Method for Obtaining Equilibria of Self-Gravitating and Rotating Gases
• S. W. Stahler (1983, ApJ, 268, 155 - 184) — The Equilibria of Rotating, Isothermal Clouds. I. - Method of Solution
• Y. Eriguchi (1978, PASJ, 30, 507 - 518) — Hydrostatic Equilibria of Rotating Polytropes
• S. I. Blinnikov (1975, Soviet Astronomy, 19, 151 - 156) — Self-Consistent Field Method in the Theory of Rotating Stars
• M. J. Clement (1974, ApJ, 194, 709 - 714) — On the Solution of Poisson's Equation for Rapidly Rotating Stars
• S. Jackson (1970, ApJ, 161, 579 - 585) — Rapidly Rotating Stars. V. The Coupling of the Henyey and the Self-Consistent Methods
• J. P. Ostriker & J. W.-K. Mark (1968, ApJ, 151, 1075 - 1088) — Rapidly Rotating Stars. I. The Self-Consistent-Field Method
• R. A. James (1964, ApJ, 140, 552 - 582) — The Structure and Stability of Rotating Gas Masses

Early Eriguchi Applications

• Y. Eriguchi & E. Mueller (1985, A&A, 147, 161 - 168) — Equilibrium Models of Differentially Rotating Polytropes and the Collapse of Rotating Stellar Cores
• I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 497 - 503) — Bifurcation Points on the Maclaurin Sequence
• I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 259 - 276) — Binary Fluid Star
• I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 239 - 257) — Fission of Dumbbell Equilibrium and Binary State of Rapidly Rotating Polytropes
• I. Hachisu & Y. Eriguchi (1983, MNRAS, 204, 583 - 589) — Bifurcations and Phase Transitions of Self-Gravitating and Uniformly Rotating Fluid
• I. Hachisu & Y. Eriguchi (1982, Prog. Theor. Phys., 68, 206 - 221) — Bifurcation and Fission of Three Dimensional, Rigidly Rotating and Self-Gravitating Polytropes
• I. Hachisu, Y. Eriguchi, & D. Sugimoto (1982, Prog. Theor. Phys., 68, 191 - 205) — Rapidly Rotating Polytropes and Concave Hamburger Equilibrium
• Y. Eriguchi & D. Sugimoto (1981, Prog. Theor. Phys., 65, 1870 - 1875) — Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid
• T. Fukushima, Y. Eriguchi, D. Sugimoto, G. S. Bisnovatyi-Kogan (1980, Prog. Theor. Phys., 63, 1957 - 1970) — Concave Hamburger Equilibrium of Rotating Bodies

Other Example Applications

• E. Mueller & Y. Eriguchi (1985, A&A, 152, 325 - 335) — Equilibrium Models of Differentially Rotating, Completely Catalyzed, Zero-Temperature Configurations With Central Densities Intermediate to White Dwarf and Neutron Star Densities
• J. R. Ipser & R. A. Managan (1981, ApJ, 250, 362 - 372) — On the Existence and Structure of Inhomogeneous Analogs of the Dedekind and Jacobi Ellipsoids
• C. T. Cunningham (1977, ApJ, 211, 568 - 578) — Rapidly Rotating Spheroids of Polytropic Index n = 1
• R. H. Durisen (1975, ApJ, 199, 179 - 183) — Upper Mass Limits for Stable Rotating White Dwarfs
• P. Bodenheimer & J. P. Ostriker (1973, ApJ, 180, 159 - 170) — Rapidly Rotating Stars. VIII. Zero-Viscosity Polytropic Sequences'
• P. Bodenheimer (1971, ApJ, 167, 153 - 163) — Rapidly Rotating Stars. VII. Effects of Angular Momentum on Upper-Main-Sequence Models
• P. Bodenheimer & J. P. Ostriker (1970, ApJ, 161, 1101 - 1113) — Rapidly Rotating Stars. VI. Pre-Main-Sequence Evolution of Massive Stars
• R. Kippenhahn & H.-C. Thomas (1970) in Proceedings of the 4th IAU Colloquium, held at the Ohio State University, Columbus, Ohio, September 8 - 11, 1969, Dordrecht: Riedel Publishing Co., edited by A. Slettebak — Stellar Rotation ==> Purchase proceedings from Springer, from Australia, or from Google
  • In the introductory section of his paper, S. Jackson (1970) references this article by Kippenhahn & Thomas in the context of uniformly rotating, and therefore only mildly distorted, structures.
• J. P. Ostriker & J. L. Tassoul (1969, ApJ, 155, 987 - ) — On the Oscillations and Stability of Rotating Stellar Models. II. Rapidly Rotating White Dwarfs
• M. J. Clement (1969, ApJ, 156, 1051 - 1068) — Differential Rotation in Stars on the Upper Main Sequence
• J. W.-K. Mark (1968, ApJ, 154, 627 - ) — Rapidly Rotating Stars. III. Massive Main-Sequence Stars
• J. P. Ostriker & P. Bodenheimer (1968, ApJ, 151, 1089 - ) — Rapidly Rotating Stars. II. Massive White Dwarfs
• J. Faulkner, I. W. Roxburgh, & P. A. Strittmatter (1968, ApJ, 151, 203 - 216) — Uniformly Rotating Main-Sequence Stars
• R. Stoeckly (1965, ApJ, 142, 208 - 228) — Polytropic Models with Fast, Non-Uniform Rotation
  • In the introductory section of his paper, S. Jackson (1970) states that a differentially rotating polytropic structure with a rotationally induced extreme distortion was first illustrated in this article by Stoeckly.

Henyey Technique for Nonrotating Stars

• L. G. Henyey, L. Wilets, K. H. Böhm, R. Lelevier, & R. D. Levee (1959, ApJ, 129, 628 - ) — A Method for Automatic Computation of Stellar Evolution
• L. G. Henyey, J. E. Forbes, & N. L. Gould (1964, ApJ, 139, 306 - ) — A New Method of Automatic Computation of Stellar Evolution

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation