User:Tohline/Apps/DysonWongTori

From VistrailsWiki
Jump to navigation Jump to search

Self-Gravitating, Incompressible (Dyson-Wong) Tori

Much of the introductory material of this chapter has been drawn from the paper by Tohline & Hachisu (1990) titled, The Breakup of Self-Gravitating Rings, Tori, and Accretion Disks.

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Overview

In his pioneering work, F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.

Individual Works

Wong (1973, 1974)

In a paper titled, Toroidal Figures of Equilibrium, C.-Y. Wong (1974, ApJ, 190, 675 - 694) remarks that a "detailed analysis of toroidal figure of equilibrium has not received much attention since the last century. Previous work on this problem was carried out by":

Wong argues that a "reexamination of the toroidal figures of equilibrium is … necessary, because in all the previous analyses the physical quantities are expanded as a power series of the inverse of the aspect ratio. Such an expansion breaks down in the interesting region of small aspect ratios where one wishes to observe the transition between the Maclaurin sequence to the toroidal sequence. Furthermore, the classical solutions … can only treat small perturbations from a circular meridian …"

Principal Simplification: Following Poincaré, Dyson, and Kowalewsky, Wong confines his analysis to toroidal structures that have (a) uniform and incompressible mass distribution, and throughout which (b) the angular velocity is assumed to be independent of positions.

It is worth pointing out that Wong pursued this astrophysically relevant research problem at a time when, apparently, the principal focus of his work was nuclear physics. We suspect this is the case because, (a) his byline lists Oak Ridge National Laboratory as his employer; (b) in the acknowledgement section of his paper, Wong states that he "is indebted to Professor J. A. Wheeler who either consciously or unconsciously introduced the author to the subject matter with his toroidal geons and toroidal nuclei;" and Wong references and draws upon a paper that he published one year earlier — specifically, C.-Y. Wong (1973, Annals of Physics, 77, 279 - 353) — titled, Toroidal and Spherical Bubble Nuclei.

Introducing Toroidal Coordinates

Figure 1 extracted without modification from C.-Y. Wong (1973)

 "Toroidal and Spherical Bubble Nuclei'"

Annals of Physics, vol. 77, pp. 279 - 353 © Elsevier Science

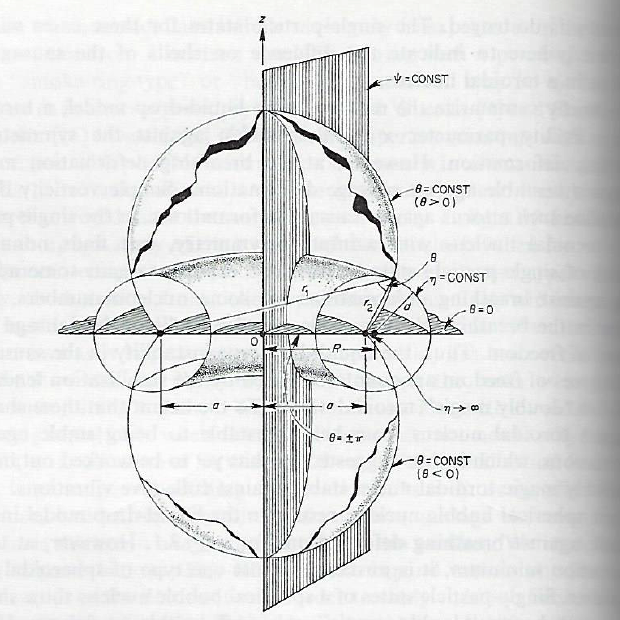
Wong (1973, Annals of Physics, 77, p. 284)

C.-Y. Wong (1973) introduces the toroidal coordinate system <math>~(\eta, \theta, \psi)</math> as follows (direct quotes from the article are displayed here in a dark green font). Referencing the figure — shown here on the right — that has been extracted without modification from the article, the surfaces of constant <math>~\eta</math> are generated by rotating a circle about the axis of symmetry, the <math>~z</math>-axis. These surfaces are toroidal surfaces. A toroidal surface of coordinate <math>~\eta</math> can be characterized by a "major radius" <math>~R</math> and a "minor radius" <math>~d</math> … The quantity <math>~\eta</math> varies from zero to infinity. The larger the value of <math>~\eta</math>, the smaller is the "minor radius" <math>~d</math>; when <math>~\eta</math> approaches infinity, the two-dimensional toroidal surface degenerates into a 1-dimensional circle with a radius <math>~a</math>. [Note that, otherwise, <math>~R</math> (the location of the center of the circular cross-section of the torus) does not coincide with <math>~a</math> (the location of the off-axis "origin" of the toroidal coordinate system).] The surfaces of constant <math>~\theta</math> are spherical bowls. The coordinate <math>~\theta</math> is defined in such a way that points above the x-y plane are characterized by positive values of <math>~\theta</math> while points below the x-y plane by negative values of <math>~\theta</math>. Thus — as is the case for a traditional spherical coordinate system — <math>~\theta</math> varies from <math>~- \pi</math> to <math>~+\pi</math>. As is also the case for a spherical coordinate system, the surfaces of constant <math>~\psi</math> are half planes through the axis of symmetry. The coordinate <math>~\psi</math> varies from <math>~0</math> to <math>~2\pi</math>.

Given a toroidal surface of major radius <math>~R</math> and minor radius <math>~d</math>, the parameter <math>~a</math> is defined such that,

<math>~a^2</math>

<math>~\equiv</math>

<math>~R^2 - d^2 \, ,</math>

Wong (1973), Eq. (2.8)

and the corresponding "radial" coordinate location <math>~\eta_0</math> of the relevant toroidal surface is,

<math>~\eta_0</math>

<math>~=</math>

<math>~\cosh^{-1}\biggl(\frac{R}{d}\biggr) \, .</math>

Wong (1973), Eq. (2.9)

Alternatively, given <math>~\eta_0</math> and the value of the parameter <math>~a</math>, we have,

<math>~R</math>

<math>~=</math>

<math>~a \coth\eta_0 \, ,</math>

<math>~d</math>

<math>~=</math>

<math>~\frac{a}{\sinh\eta_0} \, .</math>

Wong (1973), Eqs. (2.10) & (2.11)

Hence, the aspect ratio is,

<math>~\frac{R}{d}</math>

<math>~=</math>

<math>~\cosh\eta_0 \, .</math>

Wong (1973), Eq. (2.12)

Given the value of the scale-length, <math>~a</math>, the relationship between toroidal coordinates and Cartesian coordinates is [see equations 2.1 - 2.3 of Wong (1973)],

<math>~x</math>

<math>~=</math>

<math>~\frac{a \sinh\eta \cos\psi}{(\cosh\eta - \cos\theta)} \, ,</math>

<math>~y</math>

<math>~=</math>

<math>~\frac{a \sinh\eta \sin\psi}{(\cosh\eta - \cos\theta)} \, ,</math>

<math>~z</math>

<math>~=</math>

<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, ;</math>

or, mapping the other direction [see equations 2.13 - 2.15 of Wong (1973),

<math>~\eta</math>

<math>~=</math>

<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math>

<math>~\cos\theta</math>

<math>~=</math>

<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math>

<math>~\tan\psi</math>

<math>~=</math>

<math>~\frac{y}{x} \, ,</math>

where,

<math>~r_1^2 </math>

<math>~\equiv</math>

<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math>

<math>~r_2^2 </math>

<math>~\equiv</math>

<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math>

Comment by J. E. Tohline on 16 August 2017: In equation (2.17) of his §IIB — when Wong (1973) introduces the differential volume element — the variable used to represent the azimuthal coordinate angle switches from ψ to Φ. We will stick with the ψ notation, here.

and <math>~\theta</math> has the same sign as <math>~z</math>. Drawing from equations (2.7), (2.17) and (2.18) of Wong (1973), we see that the volume, <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is,

<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math>

<math>~=</math>

<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math>

If <math>~\eta_s \rightarrow \eta_0</math> then, in terms of the major and the minor radii of the torus, the volume is,

<math>~V</math>

<math>~=</math>

<math>~2\pi^2 Rd^2 \, .</math>

Wong (1973), Eq. (2.19)

If such a torus has a uniform density, <math>~\rho_0</math>, throughout, and a total charge (mass), <math>~q</math>, then the charge (mass) and density will be related through the toroidal-coordinate expression (see Wong's equation 2.51),

<math>~\rho_0 = \frac{q}{V}</math>

<math>~=</math>

<math>~\frac{q\sinh^3\eta_0}{2\pi^2 a^3 \cosh{\eta_0}} \, .</math>

Also, as Wong (1973) points out (see his equation 2.50), in this case the density distribution may be written as,

<math>~\rho(\eta^', \theta^', \psi^')</math>

<math>~=</math>

<math>~\rho_0 \Theta(\upsilon) \, ,</math>

where, the argument <math>~\upsilon \equiv (\eta - \eta_s)</math>, and <math>~\Theta(\upsilon)</math> is the step function defined by,

<math>~\Theta(\upsilon)</math>

<math>~=</math>

<math>~0</math>

     for  <math>~\upsilon < 0 \, ,</math>

<math>~\Theta(\upsilon)</math>

<math>~=</math>

<math>~1</math>

     for  <math>~\upsilon \ge 0 \, .</math>

The Coulomb Potential

As Wong (1973) reminds us, the Coulomb potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary charge distribution, <math>~\rho({\vec{r}})</math>, is,

<math>~U({\vec{r}}~')</math>

<math>~=</math>

<math>~\iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math>

Referencing, for example, equation (3) of Cohl and Tohline (1999), we see that if we let <math>~\rho({\vec{r}})</math> represent a mass distribution instead of a charge distribution, this identical expression will give the Newtonian gravitational potential if we simply multiply through by (conventionally, the negative of) the gravitational constant, <math>~G</math>.

From the above expression for the differential volume element in toroidal coordinates, the right-hand side of this expression for the potential becomes,

<math>~U(\eta^',\theta^',\psi^')</math>

<math>~=</math>

<math>~\rho_0 a^3 \iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ \, .</math>

Wong (1973), Eq. (2.52)

Next, Wong (1973) points out that in toroidal coordinates the Green's function is,

<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math>

<math>~=</math>

<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math>

 

 

<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math>

Wong (1973), Eq. (2.53)

where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>. After plugging this Green's function into the expression for the potential, then integrating over the azimuthal angle — which is permitted, here, because the density distribution, <math>~\rho(\vec{r})</math>, is assumed to be axisymmetric — Wong (1973) obtains,

<math>~U(\eta^',\theta^')</math>

<math>~=</math>

<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math>

 

 

<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math>

Wong (1973), Eq. (2.55)

which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain,

<math>~U(\eta^',\theta^')</math>

<math>~=</math>

<math>~ \frac{2^{9 / 2}\rho_0 a^2}{3} (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \cos(n\theta^') \int_{\eta_0}^\infty d\eta \biggl[ \frac{Q^2_{n-1 / 2}(\cosh\eta)}{\sinh\eta} \biggr] </math>

 

 

<math>~ \times \begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, . </math>

Wong (1973), Eq. (2.57)

TO BE DONE:


As we have suggested in an accompanying discussion, this expression should match our separate "special case" evaluation of the potential of a uniform-density torus if this expression is evaluated at <math>~\eta^' = +\infty</math>, and all values of the polar angle, <math>~\theta^'</math>.

Finally, Wong (1973) was able to complete the integration over the radial coordinate, <math>~\eta</math> to obtain an expression for the potential — most generally, his equation (2.59) — at all interior as well as all exterior coordinate positions, <math>~(\eta^', \theta^')</math>. Here, we will present only the interior solution, which is:

<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math>

<math>~=</math>

<math>~ \frac{2^{3 / 2}}{3\pi^2} \biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math>

 

 

<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math>

Wong (1973), Eq. (2.65)

where,

<math>~B_n(\cosh\eta_0)</math>

<math>~\equiv</math>

<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math>

Wong (1973), Eq. (2.62)

See Also

  1. Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"


 

Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/Apps/DysonWongTori&oldid=14578"