Difference between revisions of "User:Tohline/2DStructure/ToroidalCoordinates"
(→Statement of the Problem: Finish describing test model with uniform density and circular cross-section) |
(→Using Toroidal Coordinates to Determine the Gravitational Potential: tentative save) |
||
| Line 97: | Line 97: | ||
===Chosen Test Mass Distribution=== | ===Chosen Test Mass Distribution=== | ||
For purposes of illustration, we will follow the lead of [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T | For purposes of illustration, we will follow the lead of [http://adsabs.harvard.edu/abs/2012MNRAS.424.2635T Trova, Huré & Hersant (2012)] — see the left-hand panel of the following figure ensemble — and seek to determine the gravitational potential, both inside and outside, of a uniform-density, equatorial-plane torus whose (pink) meridional cross-section is exactly a circle. More specifically, as illustrated in our Figure 1 — see the right-hand panel of the following figure ensemble — at all azimuthal angles, a cross-section through the (pink) torus is prescribed by the algebraic expression, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 137: | Line 137: | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
==Toroidal Coordinates== | |||
Here we highlight certain properties and features of the MF53 toroidal coordinate system; more details can be found in a [[User:Tohline/Appendix/Ramblings/ToroidalCoordinates#Toroidal_Coordinates|related set of our online notes]]. Most importantly in the context of our discussion, if (in all meridional planes) the origin of the toroidal coordinate system is placed at the ''cylindrical-coordinate'' location, <math>~(a, Z_0), </math> the pair of orthogonal coordinates, <math>~(\xi_1, \xi_2)</math>, in the toroidal coordinate system is related to the cylindrical coordinate pair, <math>~(\varpi, Z)</math>, via the expressions, | |||
<table align="center" border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\frac{(Z_0 - Z)}{a} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math> | |||
~= | |||
</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\frac{\varpi}{a} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math> | |||
~= | |||
</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
An off-center circle — such as the black circle depicted in our Figure 1 diagram — is generated If a value of the "radial" coordinate, <math>~\xi_1</math>, is chosen from within the range, | |||
<div align="center"> | |||
<math> | |||
+1 \leq \xi_1 < \infty\, , | |||
</math> | |||
</div> | |||
and held fixed while the "angular" coordinate, <math>~\xi_2</math>, is varied over the range, | |||
<div align="center"> | |||
<math> | |||
~ -1 \leq \xi_2 \leq +1 . | |||
</math> | |||
</div> | |||
The inner and outer edges of the toroidal-coordinate surface in the <math>~Z = Z_0</math> plane are determined by setting <math>~\xi_2 = -1</math> (inner) and <math>~\xi_2 = +1</math> (outer). Hence, | |||
<table align="center" border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\chi_\mathrm{inner} | |||
</math> | |||
</td> | |||
<td align="center> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\chi_\mathrm{outer} | |||
</math> | |||
</td> | |||
<td align="center> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
The equatorial-plane location of the "center" of each torus is, | |||
<div align="center"> | |||
<math> | |||
\chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} , | |||
</math> | |||
</div> | </div> | ||
Revision as of 22:52, 5 October 2015
Using Toroidal Coordinates to Determine the Gravitational Potential
The detailed derivations and associated scratch-work that support the summary discussion of this chapter can be found under the Appendix/Ramblings category of this H_Book.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Preamble
As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?
I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.1 (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.
I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened (especially axisymmetric) configurations.2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind — see NIST digital library discussion — where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system — see more on this, below.
Statement of the Problem
Expression for the Axisymmetric Potential
Cohl & Tohline (1999; hereafter CT99) derive an expression for the Newtonian gravitational potential in terms of a Compact Cylindrical Green's Function expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the potential at any meridional location, <math>\varpi = a</math> and <math>~Z = Z_0</math>, due to an axisymmetric mass distribution, <math>~\rho(\varpi, Z)</math>, is
<math> \Phi(a,Z_0) = - \frac{2G}{a^{1/2}} q_0 , </math>
where,
<math> q_0 = \int\int \varpi^{1/2} Q_{-1/2}(\Chi) \rho(\varpi, Z) d\varpi dZ, </math>
and the dimensionless argument (the modulus) of the special function, <math>~Q_{-1/2}</math>, is,
<math> \Chi \equiv \frac{a^2 + \varpi^2 + (Z_0 - Z)^2}{2a \varpi} . </math>
Next, following the lead of CT99, we note that according to the Abramowitz & Stegun (1965),
<math>Q_{-1/2}(\Chi) = \mu K(\mu) \, ,</math>
where, the function <math>~K(\mu)</math> is the complete elliptical integral of the first kind and, for our particular problem,
|
<math>~\mu^2</math> |
<math>~\equiv</math> |
<math>~2(1+\Chi)^{-1}</math> |
|
|
<math>~=</math> |
<math>~ 2\biggl[ 1+\frac{a^2 + \varpi^2 + (Z_0 - Z)^2}{2a \varpi}\biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4a\varpi}{(a + \varpi)^2 + (Z_0 - Z)^2} \biggr] \, . </math> |
Hence, we can write,
<math> q_0 = \int\int \varpi^{1/2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, . </math>
As has been explained in an accompanying set of notes, this is precisely the same expression for the gravitational potential that A. Trova, J.-M. Huré and F. Hersant (2012; MNRAS, 424, 2635) used in their study of the potential of self-gravitating, axisymmetric discs.
Our objective, here, is to examine whether or not it might be advantageous to transform this expression to one in which the double integral is performed on a toroidal, rather than a cylindrical, coordinate system.
Chosen Test Mass Distribution
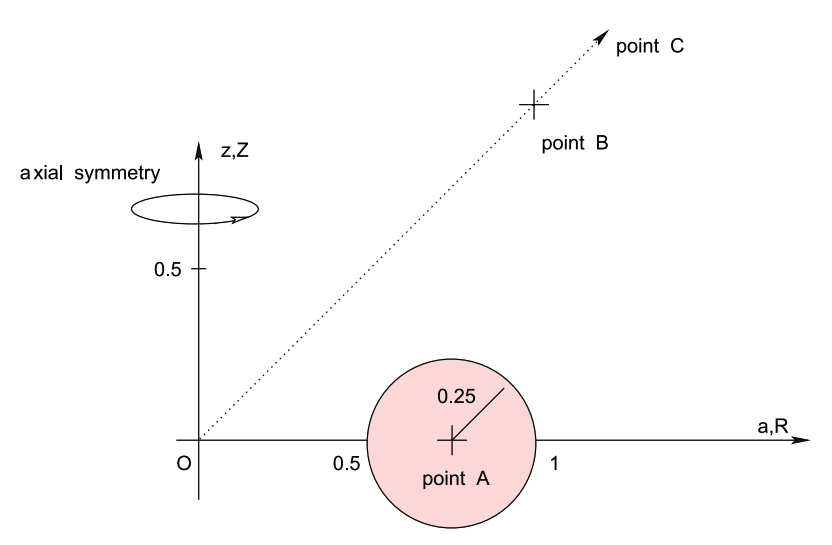
For purposes of illustration, we will follow the lead of Trova, Huré & Hersant (2012) — see the left-hand panel of the following figure ensemble — and seek to determine the gravitational potential, both inside and outside, of a uniform-density, equatorial-plane torus whose (pink) meridional cross-section is exactly a circle. More specifically, as illustrated in our Figure 1 — see the right-hand panel of the following figure ensemble — at all azimuthal angles, a cross-section through the (pink) torus is prescribed by the algebraic expression,
|
<math>~(\varpi_t - \varpi)^2 + Z^2</math> |
<math>~=</math> |
<math>~r_t^2 \, .</math> |
Everywhere inside this toroidal surface we set <math>~\rho(\varpi, Z) = \rho_0</math>, that is, the density is uniform with the value, <math>~\rho_0</math>.
|
Figure 4 extracted without modification from p. 2640 of Trova, Huré & Hersant (2012)
"The Potential of Discs from a 'Mean Green Function' "
Monthly Notices of the Royal Astronomical Society, vol. 424, pp. 2635-2645 © RAS |
Our Figure 1 |
|---|---|
Toroidal Coordinates
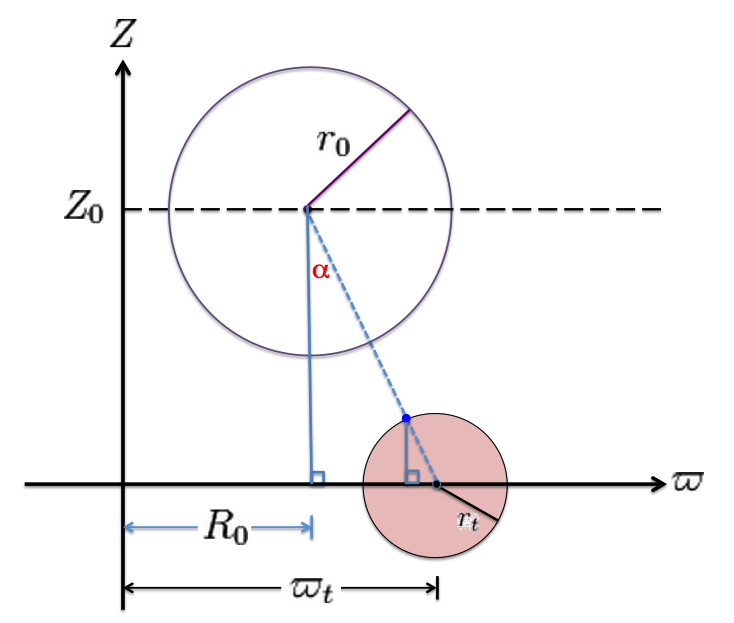
Here we highlight certain properties and features of the MF53 toroidal coordinate system; more details can be found in a related set of our online notes. Most importantly in the context of our discussion, if (in all meridional planes) the origin of the toroidal coordinate system is placed at the cylindrical-coordinate location, <math>~(a, Z_0), </math> the pair of orthogonal coordinates, <math>~(\xi_1, \xi_2)</math>, in the toroidal coordinate system is related to the cylindrical coordinate pair, <math>~(\varpi, Z)</math>, via the expressions,
|
<math> ~\frac{(Z_0 - Z)}{a} </math> |
<math> ~= </math> |
<math> ~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, , </math> |
|
<math> ~\frac{\varpi}{a} </math> |
<math> ~= </math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, . </math> |
An off-center circle — such as the black circle depicted in our Figure 1 diagram — is generated If a value of the "radial" coordinate, <math>~\xi_1</math>, is chosen from within the range,
<math> +1 \leq \xi_1 < \infty\, , </math>
and held fixed while the "angular" coordinate, <math>~\xi_2</math>, is varied over the range,
<math> ~ -1 \leq \xi_2 \leq +1 . </math>
The inner and outer edges of the toroidal-coordinate surface in the <math>~Z = Z_0</math> plane are determined by setting <math>~\xi_2 = -1</math> (inner) and <math>~\xi_2 = +1</math> (outer). Hence,
|
<math> ~\chi_\mathrm{inner} </math> |
<math>~=</math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} </math> |
|
<math> ~\chi_\mathrm{outer} </math> |
<math>~=</math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} </math> |
The equatorial-plane location of the "center" of each torus is,
<math> \chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} , </math>
See Also
References
- Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
- Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
- Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |