User:Tohline/vtk/SimpleCubeTutorial/CubeDetails
Cube Definition Details

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
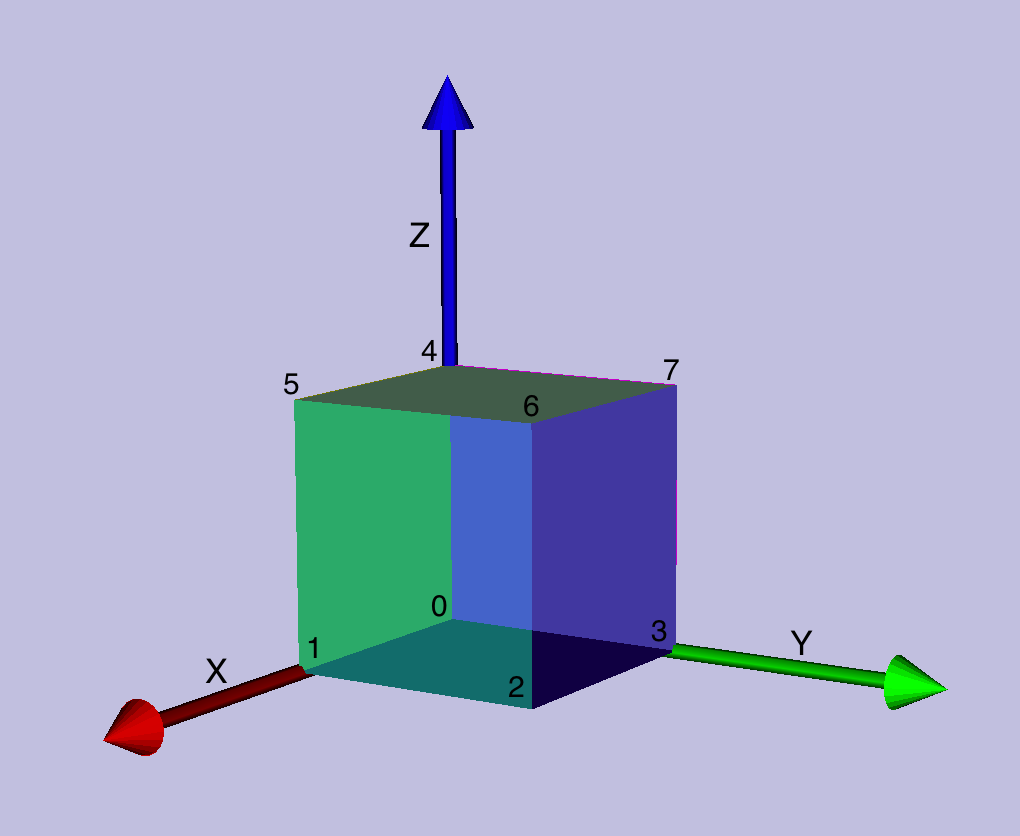
A model of virtually any three-dimensional structure can be fed into VisTrails — and understood by the accompanying visualization toolkit (vtk) library of routines — using VTK's Simple Legacy Format. Here we explain how the set of vertices (POINTS) and POLYGONS of a simple cube can be defined using this Simple Legacy Format; this explanation is primarily intended to provide supplemental details for our accompanying Simple Cube Tutorial.
|
Defining the POINTS (vertices) & POLYGONS of a cube in Simple Legacy Format |
|
|---|---|
# vtk DataFile Version 2.0 Cube example ASCII DATASET POLYDATA POINTS 8 float 0.0 0.0 0.0 1.0 0.0 0.0 1.0 1.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 1.0 0.0 1.0 1.0 1.0 1.0 0.0 1.0 1.0 POLYGONS 6 30 4 0 1 2 3 4 4 5 6 7 4 0 1 5 4 4 2 3 7 6 4 0 4 7 3 4 1 2 6 5 |
<== (x,y,z) coordinates of POINT "0" <== ... of POINT "1" <== ... of POINT "2" <== ... of POINT "3" <== ... of POINT "4" <== ... of POINT "5" <== ... of POINT "6" <== ... of POINT "7" <== (see explanation in the accompanying text) <== POLYGON "0": A four-sided polygon formed by connecting POINTS 0, 1, 2, & 3, in that order. <== POLYGON "1": A four-sided polygon formed by connecting POINTS 4, 5, 6, & 7, in that order. <== POLYGON "2": A four-sided polygon ... POINTS 0, 1, 5, & 4, in that order. <== POLYGON "3": A four-sided polygon ... POINTS 2, 3, 7, & 6, in that order. <== POLYGON "4": A four-sided polygon ... POINTS 0, 4, 7, & 3, in that order. <== POLYGON "5": A four-sided polygon ... POINTS 1, 2, 6, & 5, in that order. |
|
Input Data File in |
Annotation to aid in interpretation of individual lines of text/data from the input data file. |
Simple Legacy Format
The lines of data presented on the left in the caption to the above figure are sufficient to define a simple cube. In order to interpret the meaning of each line, start with the appreciation that a cube has 8 corners (also referred to as vertices or "POINTS") and six faces. Each face of the cube is a four-sided polygon which, itself, can be defined by properly connecting subsets of the 8 POINTS.
- When a Simple Legacy Format "reader" within the visualization toolkit (VTK) library sees a line of text that reads "DATASET POLYDATA," it expects that the subsequent sequence of lines of text/data will define all of the POINTS and POLYGONS that are needed to graphically build the desired object — in this case, a cube.
Specifying the location of the cube's corners/vertices
- The line of text that reads "POINTS 8 float" means that the subsequent 8 lines will, in sequence, provide the <math>~(x,y,z)</math> coordinates of the 8 corners of the cube; for each POINT the coordinate values will be provided as a triplet set of floating point numbers. As VTK reads in each triplet set of coordinates, it will (internally) assign a number to the POINT, starting with the number zero and incrementing by one so that, for example, the eighth point will be referenced as POINT "7".
- On the rendered color image of the cube, shown above, we have labeled each corner of the cube with the number that it will be assigned (internally by VTK), given the order in which the POINT's coordinates appear in the data file. For example, the first coordinate triplet <math>~(x,y,z) = (0,0,0)</math> (i.e., the origin in Cartesian coordinates) is understood to be POINT "0," and the corner of the cube that is farthest from the origin with <math>~(x,y,z) = (1,1,1)</math> is understood to be POINT "6."
- It really doesn't matter in what order the POINTS appear in the data file — for example, the origin could have been the eighth coordinate triplet entry, in which case the origin would be labeled POINT "7."
Defining the cube's six quadrilateral faces
- The line of text that reads "POLYGONS 6 30" means that the subsequent 6 lines will, in sequence, identify the group of POINTS that should be connected to define the complete perimeter of each face of the cube. For example, POINTS 0, 1, 2, & 3 should be connected in order to create the cube face (POLYGON "0") that lies in the x-y plane — shown in the above image as the bottom of the cube.
- Each line of POLYGON-defining data must begin with an integer that tells the VTK reader how many additional integer numbers will appear on that line in order to define the desired polygon. In the case being illustrated here, each of the 6 cube faces is being specified as a quadrilateral, so the first integer that appears in all six lines of POLYGON-defining data is "4."
- In total, the VTK reader must read in six lines of data with five integer numbers per line, for a total of <math>~6\times 5 = 30</math> integers, in order to completely understand how the cube is to be drawn. This is why the integer "30" appears in the instructional heading, "POLYGONS 6 30."
Identifying the normal to each cube face
- It is important to appreciate that, when identifying the POINTS that will define any individual POLYGON, the order in which the POINTS are identified matters. VTK will draw the perimeter of the polygon by connecting the points in the specified order. For example, the top face of the cube (POLYGON "1"), as illustrated above, has been properly drawn because the line of data defining that quadrilateral reads "4 4 5 6 7"; VTK understands that the perimeter of that desired polygon will be traversed by connecting POINT 4 to POINT 5 to POINT 6 to POINT 7, then back to POINT 4. The same desired result could be achieved by providing a line of data that reads "4 6 7 4 5," but the proper polygon would not have been drawn if the line of data read "4 5 7 6 4."
- For visualization purposes, it is useful to catalog the orientation of the unit vector that is normal to the face of each polygon. (It is straightforward to make this identification because each defined polygon is assumed to be perfectly flat.1) But there will always be a sign ambiguity; is the unit vector pointing "up," or is it pointing "down." For example, POLYGON "1" in the above illustration — the face on the top of the cube — lies parallel to the x-y plane, so the unit vector that is normal to its surface points in the z-direction. But is it pointing in the plus z-direction or the "minus" z-direction? In order to resolve this ambiguity, by default VTK uses the right-hand rule when assigning a NORMAL to each polygon. More specifically, as the POINTS are being connected in sequence to define each POLYGON, VTK assumes that it is traversing the polygon's perimeter in a counter-clockwise direction and that the unit normal points "up" as would be indicated by the direction that the thumb on your right hand points as the fingers on your right hand are also curling counter-clockwise. Hence, referring back to POLYGON "1" in our simple cube example, for which the relevant line of input data reads "4 4 5 6 7," VTK will record (internally) that the NORMAL to POLYGON "1" points in the plus z direction. Put another way, the unit vector that sits normal to POLYGON "1" points in the <math>~(x,y,z) = (0,0,1)</math> direction.
- It is possible to override VTK's default specification of the NORMAL for any given POLYGON. Within the context of the Simple Legacy Format, this is done by explicitly assigning a triplet of integers (or floating point numbers) to every POLYGON as part of the "CELL_DATA" specification and under an optional "NORMALS" subcategory of the input data file.
1This is certainly true for our illustrated cube and, I presume, it is VTK's default presumption. With this in mind, it is safest and easiest to build all structures using 3-sided polygons — that is, triangles — because the three POINTS that define each triangle are guaranteed to lie in the same plane.