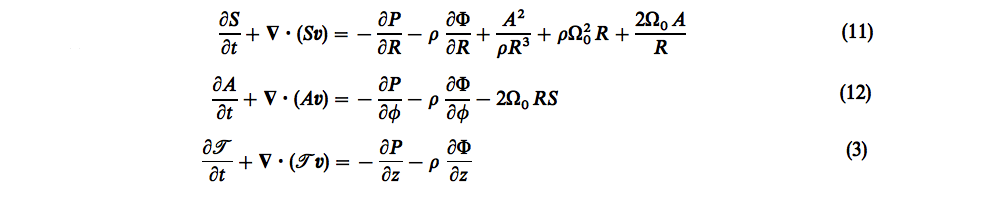User:Tohline/PGE/Hybrid Scheme
Hybrid Advection Scheme
Preface
March 1, 2014 by Joel E. Tohline
<full preface> … This seemed too good to be true. The discovered code modification would allow us to conserve angular momentum very accurately and, at the same time, allow us to use a rotating grid and thereby minimize numerical diffusion … <read more>
In his dissertation research, Jay Call (see Call, Tohline, & Lehner 2010) derived a complete description of this hybrid advection scheme in a fully relativistic and generalized coordinate framework. He showed that one can write the system of fluid equations in a manner that facilitates advection of inertial-frame quantities across a rotating grid. In addition — and more importantly — he showed how to write the system of fluid equations to allow advection of inertial-frame angular momentum (generally associated with a cylindrical coordinate mesh) across a rotating Cartesian grid. Since that time, primarily in the context of Zach Byerly's doctoral dissertation research, my group has demonstrated that this hybrid advection scheme works extremely well (see Byerly, Adelstein-Lelbach, Tohline, & Marcello (2014)). In the discussion that follows here, we derive the Newtonian version of Jay's hybrid scheme.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Setting the Stage
Recognizing Statements of Conservation
When dealing with the compressible fluid equations, we will often encounter hyperbolic PDEs of the following form:
|
<math> \frac{d\psi}{dt} + \psi \nabla\cdot \vec{v} </math> |
<math>~=~</math> |
<math> S \, , </math> |
where we are using <math>~\vec{v}</math> to represent the velocity field of the fluid as viewed from an inertial frame of reference, and the total (as opposed to partial) time derivative indicates the time-rate of change of <math>~\psi</math> is being measured in a so-called Lagrangian fashion, that is, at the location of some fluid element and moving along with that fluid element.
When we encounter a situation in which the "source" term, <math>~S</math>, on the right-hand side is zero, we will be able to identify the scalar variable, <math>~\psi</math>, as the volume density of some conserved quantity. For example, the continuity equation — which is a mathematical statement of mass conservation — has the form,
|
or, equivalently, |
<math> \frac{d\ln\rho}{dt} </math> |
<math>~=~</math> |
<math> ~- \nabla\cdot \vec{v} \, , </math> |
where, <math>~\rho</math> is the mass per unit volume or, simply, the mass density of the fluid element. Clearly, when the mass of a Lagrangian fluid element is conserved, the fluid element's mass density changes only in accordance with the divergence of the local velocity field.
Similarly, if we are following the evolution of a fluid that expands and contracts adiabatically, we should expect to encounter an equation of the form,
|
<math> \frac{ds}{dt} + s\nabla\cdot \vec{v} </math> |
<math>~=~</math> |
<math> 0 \, , </math> |
or, equivalently, |
<math> \frac{d\ln s}{dt} </math> |
<math>~=~</math> |
<math> ~- \nabla\cdot \vec{v} \, , </math> |
where, <math>~s</math> is the entropy density of a Lagrangian fluid element. Or, if an axisymmetric distribution of fluid is moving in an axisymmetric potential, we should expect the azimuthal component of the fluid's angular momentum to be conserved, in which case we should expect to encounter a dynamical equation of the form,
|
<math> \frac{d(\rho \varpi v_\phi)}{dt} + (\rho \varpi v_\phi) \nabla\cdot \vec{v} </math> |
<math>~=~</math> |
<math> 0 \, , </math> |
where, <math>~\varpi</math> is the Lagrangian fluid element's (cylindrical radial) distance measured from the symmetry axis of the underlying potential and <math>~v_\phi = \varpi\dot\phi</math> is the azimuthal component of the inertial velocity field, <math>~\vec{v}</math>, at the location of the fluid element.
Alternative Reference Frames
Now, we might want to examine the time-dependent behavior of a fluid system while viewing the flow from a reference frame that is more or less moving along with the fluid. This new frame of reference need not be an inertial frame; for example, when studying a rotating fluid, we may want to view the system's evolution from a rotating frame of reference. This will be accomplished mathematically by adjusting the dynamical equations so that the velocity that appears in the divergence term accounts for the new "frame" velocity field; specifically, we want to replace <math>~\vec{v}</math> with,
|
<math> \vec{u} </math> |
<math>~=~</math> |
<math> \vec{v} - \vec{v}_\mathrm{frame} \, . </math> |
(Here, we will consider only time-independent functional expressions for the frame velocity, <math>~\vec{v}_\mathrm{frame}</math>.) Of course, switching to the rotating frame must be done in such a way that the resulting, new PDE describes exactly the same physical behavior of the system as was described by the original equation; that is, the new equation must be derivable from the original one.
If <math>~\vec{v}_\mathrm{frame}</math> is a divergence-free velocity field, then the transformation is trivial. For example, if we choose a frame of reference that is rotating uniformly with angular velocity, <math>~\Omega_0</math>, then,
|
<math> \vec{v}_\mathrm{frame} </math> |
<math>~=~</math> |
<math> \boldsymbol{\hat{e}}_\phi (\varpi \Omega_0) \, , </math> |
and, utilizing cylindrical coordinates,
|
<math> \nabla\cdot\vec{v}_\mathrm{frame} </math> |
<math>~=~</math> |
<math> \frac{\partial(0)}{\partial \varpi} + \frac{1}{\varpi}\frac{\partial(\varpi \Omega_0)}{\partial \phi} + \frac{\partial(0)}{\partial z} = 0 \, . </math> |
Hence,
|
<math> \frac{d\psi}{dt} + \psi \nabla\cdot \vec{u} </math> |
<math>~=~</math> |
<math> \frac{d\psi}{dt} + \psi \nabla\cdot [\vec{v} - \vec{v}_\mathrm{frame}] </math> |
<math>~=~</math> |
<math> \frac{d\psi}{dt} + \psi \nabla\cdot \vec{v} \, , </math> |
so the new generic hyperbolic PDE becomes,
|
<math> \frac{d\psi}{dt} + \psi \nabla\cdot \vec{u} </math> |
<math>~=~</math> |
<math> S \, , </math> |
and we can be confident that this new PDE represents the physics of the system just as well as the original PDE.
Eulerian Representation
We can shift any of the PDEs from a Lagrangian to an Eulerian representation — and thereby use them to follow the time-rate of change of physical variables at a point in space that is fixed with respect to the chosen frame of reference — by using the following transformation to replace each total time derivative with a partial time derivative:
|
<math> \frac{d\psi}{dt} </math> |
<math>~~~\rightarrow~~~</math> |
<math> \frac{\partial \psi}{\partial t} + \vec{u} \cdot \nabla\psi \, . </math> |
Hence, the "new" generic hyperbolic PDE derived above can be rewritten as,
|
<math> \frac{\partial\psi}{\partial t} + \vec{u} \cdot \nabla\psi + \psi \nabla\cdot \vec{u} </math> |
<math>~=~</math> |
<math> S \, , </math> |
or, more succinctly,
|
<math> \frac{\partial\psi}{\partial t} + \nabla\cdot (\psi \vec{u} ) </math> |
<math>~=~</math> |
<math> S \, . </math> |
This equation also is broadly recognized as a conservation statement because, when <math>~S = 0</math>, the variable <math>~\psi</math> will represent the volume density of a conserved quantity.
We should emphasize that the inertial-frame version of this Eulerian conservation equation can be retrieved straightforwardly by setting <math>~\Omega_0 = 0</math>, which is equivalent to setting <math>~\vec{u} = \vec{v}</math>. It is,
|
<math> \frac{\partial\psi}{\partial t} + \nabla\cdot (\psi \vec{v}) </math> |
<math>~=~</math> |
<math> S \, . </math> |
The physics of the flow that is being described by this PDE is identical to the physics that is described by the preceding PDE. But an important distinction must be made regarding how the two equations are interpreted. The "inertial frame" version of the equation (explicitly containing <math>~\vec{v}</math>) provides the time-rate of change of <math>~\psi</math> at a fixed point in inertial space, while the "new" version (explicitly containing <math>~\vec{u}</math>) provides the time-rate of change of <math>~\psi</math> at a fixed point in our "new" rotating coordinate frame.
Angular Momentum Conservation
When the three vector components of the Euler equation (of motion) are projected onto a nonrotating cylindrical coordinate grid, the azimuthal component of the Euler equation may be written as,
|
<math> \frac{d(\rho \varpi v_\phi)}{dt} + (\rho \varpi v_\phi) \nabla\cdot \vec{v} </math> |
<math>~=~</math> |
<math> -\frac{\partial P}{\partial\phi} - \rho \frac{\partial\Phi}{\partial\phi} \, . </math> |
For this equation, the source term is identified as,
|
<math> ~S </math> |
<math>~=~</math> |
<math> -\frac{\partial P}{\partial\phi} - \rho \frac{\partial\Phi}{\partial\phi} \, , </math> |
and <math>~\psi = (\rho\varpi v_\phi)</math> is the inertial-frame angular momentum density, as measured with respect to the <math>~z</math>-coordinate axis. This corresponds the scalar equation and representation referred to as "Case B (<math>~\eta=3</math>)" in CTL (2010).
|
From Tables 6.1 & 6.2 of Call, Tohline, & Lehner (2010)
|
|
|
<math>~\psi_{(3)}</math> |
<math>~S_{(3)}</math> |
|
<math>~\rho \varpi v_\phi</math> |
<math>~ - \frac{\partial P}{\partial\phi} - \rho \frac{\partial \Phi}{\partial\phi}</math> |
As foreshadowed above — see the subsection titled, Recognizing Statements of Conservation — the angular momentum of a Lagrangian fluid element will be conserved if the "source" term, <math>~S = 0</math>. This situation will arise if, at the fluid element's location, the azimuthal pressure variation, <math>~\partial P/\partial\phi</math>, and the azimuthal variation in the gravitational potential, <math>~\partial \Phi/\partial\phi</math>, are both zero, or if the two balance one another (i.e.,<math>~\partial P/\partial\phi=-\rho\partial\Phi/\partial\phi</math>).
Based on the above discussion, we can equally well view the flow from a frame of reference that is rotating with a constant angular velocity, <math>~\Omega_0</math>, and write,
|
<math> \frac{d(\rho \varpi v_\phi)}{dt} + (\rho \varpi v_\phi) \nabla\cdot \vec{u} </math> |
<math>~=~</math> |
<math> -\frac{\partial P}{\partial\phi} - \rho \frac{\partial\Phi}{\partial\phi} \, , </math> |
where, as before,
|
<math> \vec{u} </math> |
<math>~\equiv~</math> |
<math> \vec{v} - \boldsymbol{\hat{e}}_\phi \varpi\Omega_0 \, . </math> |
Also, following the earlier discussion, if one wants to follow the time-variation of the fluid's inertial-frame angular momentum at a fixed location in inertial space, then the appropriate Eulerian representation of this azimuthal component of the equation of motion is,
|
<math> \frac{\partial (\rho \varpi v_\phi)}{\partial t} + \nabla\cdot [(\rho \varpi v_\phi) \vec{v}] </math> |
<math>~=~</math> |
<math> S \, . </math> |
If, however, one wants to follow the time-variation of the fluid's inertial-frame angular momentum at a fixed location on a rotating coordinate grid, then the appropriate Eulerian representation of this azimuthal component of the equation of motion is obtained by replacing the "transport" velocity, <math>~\vec{v}</math> with <math>~\vec{u}</math>; specifically,
|
<math> \frac{\partial (\rho \varpi v_\phi)}{\partial t} + \nabla\cdot [(\rho \varpi v_\phi) \vec{u}] </math> |
<math>~=~</math> |
<math> S \, . </math> |
An Element of the Hybrid Scheme
This last equation displays one subtle, but valuable, element of the hybrid scheme developed by Call, Tohline, & Lehner (2010). The velocity component, <math>~v_\phi</math>, that appears in the formulation of the relevant conserved quantity — the inertial-frame angular momentum density — is drawn from the velocity vector, <math>~\vec{v}</math>, which is different from the transport velocity vector, <math>~\vec{u}</math>, that defines the Eulerian frame from which the dynamical evolution of the system is being viewed. This equation is usually written, instead, in a form such that the angular momentum density is expressed in terms of the azimuthal component of the transport velocity; see, for example, equation (7) in Norman & Wilson (1978) and equation (12) in New & Tohline (1997). In this more familiar formulation, the momentum density and the transport velocity both directly refer to the same frame of reference. But, as a consequence, the source term is more complicated.
The more familiar formulation — including its modified source term — can be derived from our "hybrid" formulation by recognizing that,
|
<math> ~v_\phi </math> |
<math>~=~</math> |
<math> ~u_\phi + \varpi\Omega_0 \, . </math> |
So we can write,
|
<math> \frac{\partial [\rho \varpi (u_\phi + \varpi\Omega_0 ) ]}{\partial t} + \nabla\cdot \{[\rho \varpi ( u_\phi + \varpi\Omega_0)] \vec{u} \} </math> |
<math>~=~</math> |
<math> ~S_{\phi i} \, , </math> |
where, as shorthand, we have used,
|
<math> ~S_{\phi i} </math> |
<math>~\equiv~</math> |
<math> - \frac{\partial P}{\partial\phi} - \rho \frac{\partial \Phi}{\partial\phi} \, . </math> |
This implies,
|
<math> \frac{\partial (\rho \varpi u_\phi )}{\partial t} + \nabla\cdot [ (\rho \varpi u_\phi) \vec{u} ] </math> |
<math>~=~</math> |
<math> S_{\phi i} - \frac{\partial [\rho \varpi (\varpi\Omega_0 ) ]}{\partial t} - \nabla\cdot \{[\rho \varpi (\varpi\Omega_0)] \vec{u} \} </math> |
|
|
<math>~=~</math> |
<math> S_{\phi i} - \varpi^2\Omega_0 \biggl\{ \frac{\partial \rho}{\partial t} + \nabla\cdot (\rho \vec{u} ) \biggr\} - \rho \vec{u}\cdot \nabla(\varpi^2 \Omega_0) </math> |
|
|
<math>~=~</math> |
<math> S_{\phi i} - 2\rho \varpi u_\varpi \Omega_0 \, . </math> |
As we see, all terms involving the velocity now explicitly refer to <math>~\vec{u}</math> and, hence, to the velocity as measured in the rotating reference frame. But the source now includes a Coriolis term. This corresponds the scalar equation and representation referred to as "Case B (<math>~\eta=3'</math>)" in CTL (2010).
|
From Tables 6.1 & 6.2 of Call, Tohline, & Lehner (2010)
|
|
|
<math>~\psi_{(3')}</math> |
<math>~S_{(3')}</math> |
|
<math>~\rho \varpi (v_\phi - \varpi\Omega_0) = \rho \varpi u_\phi </math> |
<math>~ - \frac{\partial P}{\partial\phi} - \rho \frac{\partial \Phi}{\partial\phi} - 2\rho\varpi u_\varpi \Omega_0</math> |
Even Broader Generalization
As Call, Tohline, & Lehner (2010) point out, we are free to measure — and follow the evolution of — the angular momentum density with respect to any of a variety of different rotating frames of reference. Specifically, we are not constrained to choose between the inertial (nonrotating) frame — in which the measured angular momentum density is <math>~(\rho\varpi v_\phi)</math> — and the "grid" frame — in which the measured angular momentum density is <math>~\rho\varpi u_\phi = \rho\varpi(v_\phi - \varpi\Omega_0)</math>. Quite generally, we can choose to measure the angular momentum with respect to a separate "primed" frame that is rotating with angular velocity <math>~\omega_0</math> and in which the measured azimuthal component of the fluid velocity is,
<math> ~v'_\phi ~= ~v_\phi - \varpi \omega_0 \, . </math>
With this definition in hand, we also recognize that,
<math> ~u_\phi = v_\phi - \varpi\Omega_0 = v'_\phi + \varpi (\omega_0 - \Omega_0) \, . </math>
These two substitutions allow us to rewrite the angular momentum evolution equation in the forms that Call, Tohline, & Lehner (2010) label as Case C (<math>~\eta=3</math>) and Case C (<math>~\eta=3'</math>).
|
From Tables 6.1 & 6.2 of Call, Tohline, & Lehner (2010)
|
|
|
<math>~\psi_{(3)}</math> |
<math>~S_{(3)}</math> |
|
<math>~\rho \varpi (v'_\phi +\varpi\omega_0) = \rho \varpi v_\phi</math> |
<math>~ - \frac{\partial P}{\partial\phi} - \rho \frac{\partial \Phi}{\partial\phi}</math> |
|
From Tables 6.1 & 6.2 of Call, Tohline, & Lehner (2010)
|
|
|
<math>~\psi_{(3')}</math> |
<math>~S_{(3')}</math> |
|
<math>~\rho \varpi[ v'_\phi + \varpi (\omega_0 - \Omega_0)] = \rho \varpi u_\phi </math> |
<math>~ - \frac{\partial P}{\partial\phi} - \rho \frac{\partial \Phi}{\partial\phi} - 2\rho\varpi u_\varpi \Omega_0</math> |
In the latter case, <math>~v'_\phi</math> becomes <math>~u_\phi</math>, as it should, when the choice is made to measure the angular momentum density in the "grid" frame, that is, when the choice is made to set <math>~\omega_0 = \Omega_0</math>.
Zach's Dissertation Paper
Section 2.3
Building on our introductory discussion of the Euler equation (see also Appendix 1.D, §3 of BT87), we begin with the,
Lagrangian Representation
of the Euler Equation
as viewed from a Rotating Reference Frame
<math>\frac{d\mathbf{u'}}{dt} = - \frac{1}{\rho} \nabla P - \nabla \Phi - 2{\vec{\Omega}}_f \times {\mathbf{u'}} - {\vec{\Omega}}_f \times ({\vec{\Omega}}_f \times \vec{x})</math> ,
where we choose to define the frame rotation by the vector,
<math>~\vec{\Omega}_f \equiv \hat\mathbf{k} \Omega_0 \, ,</math>
and,
|
<math> ~\mathbf{u'} </math> |
<math>~=~</math> |
<math> ~\mathbf{u} - \mathbf{u}_\mathrm{frame} = \mathbf{u} - {\vec{\Omega}}_f \times \vec{x}\, , </math> |
is the velocity field as viewed from the frame of reference that is rotating at constant angular frequency, <math>~\Omega_0</math>. (Note that we can retrieve the inertial-frame Euler equation and inertial-frame variables by setting <math>~\Omega_0 = 0</math> at any point in the subsequent derivations.) Because the velocity field introduced by frame rotation is divergence free, that is, because,
|
<math> ~\nabla\cdot\mathbf{u}_\mathrm{frame} = \nabla\cdot [{\vec{\Omega}}_f \times \vec{x}] = \nabla\cdot [ {\hat\mathbf{k}} \Omega_0\times (\mathbf{\hat{e}}_R R + \mathbf{\hat{k}}z) ] </math> |
<math>~=~</math> |
<math> ~\nabla\cdot(\hat\mathbf{e}_\varphi R\Omega_0) = \frac{1}{R} \frac{\partial}{\partial\varphi} \biggl(R\Omega_0 \biggr) = 0 \, , </math> |
the relevant (rotating-frame) continuity equation is identical in form to its inertial-frame counterpart, specifically,
|
<math> \frac{d\rho}{dt} + \rho\nabla\cdot\mathbf{u'} </math> |
<math>~=~</math> |
<math> ~0 \, . </math> |
We can transform the above rotating-frame Euler equation to a momentum conservation equation by multiplying the equation through by <math>~\rho</math> and using the continuity equation to combine and simplify the left-hand-side, obtaining,
<math>\frac{d(\rho\mathbf{u'})}{dt} + (\rho\mathbf{u' })\nabla\cdot \mathbf{u'} = - \nabla P - \rho \nabla \Phi - 2\rho {\vec{\Omega}}_f \times {\mathbf{u'}} - \rho {\vec{\Omega}}_f \times ({\vec{\Omega}}_f \times \vec{x})</math> ,
In order to convert this general-purpose vector equation into the specific set of scalar component equations that embody the desired elements of our hybrid scheme, we need to:
- Step 1: Choose the unit-vector basis set associated with the momentum components that we want to track — <math>(\mathbf{\hat{i}}, \mathbf{\hat{j}}, \mathbf\hat{k})</math> if tracking linear momentum, or, <math>(\mathbf\hat{e}_R, \mathbf\hat{e}_\varphi, \mathbf\hat{k})</math> if tracking radial and angular momentum — and break the vector equation into these specified components;
- Step 2: In all relevant equations, replace the scalar components of the "rotating-frame" momentum density with the scalar components of the "intertial-frame" momentum density, drawing each component relation from the vector transformation, <math>\rho\mathbf{u'} = \rho\mathbf{u} - \rho {\vec{\Omega}}_f \times \vec{x}</math>;
- Step 3: Write all of the spatial operators in terms of spatial derivatives that are associated with the unit-vector basis set of the desired computational mesh.
Focus on Tracking Linear Momentum
Step 1
If the focus is on tracking linear momentum components, then we need to break the vector momentum equation into its <math>(\mathbf\hat{i}, \mathbf\hat{j}, \mathbf\hat{k})</math> components. This is done by, in turn, "dotting" each unit vector into the vector equation. It is straightforward once we appreciate that the orientation of these Cartesian unit vectors does not vary in space and that, within the context of the rotating frame on which they are defined, these unit vectors do not vary in time. Hence, the first term in the vector equation — the material time derivative — can be written as,
<math> \frac{d(\rho\mathbf{u'})}{dt} = \frac{d}{dt} [ \mathbf{\hat{i}} (\rho u'_x) + \mathbf{\hat{j}} (\rho u'_y) + \mathbf{\hat{k}} (\rho u'_z) ] = \mathbf{\hat{i}} \frac{d(\rho u'_x)}{dt} + \mathbf{\hat{j}} \frac{d(\rho u'_y)}{dt} + \mathbf{\hat{k}} \frac{d(\rho u'_z)}{dt} \, , </math>
and the process of "dotting" each unit vector into the equation leads to the following set of scalar momentum-component equations:
|
<math>\mathbf{\hat{i}}:</math> |
<math> \frac{d(\rho u'_x)}{dt} + (\rho u'_x)\nabla\cdot \mathbf{u'} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{i}}\cdot\nabla P - \rho \mathbf{\hat{i}}\cdot\nabla \Phi + 2\rho \mathbf{\hat{i}}\cdot[\mathbf{\hat{i}}\Omega_0 u'_y - \mathbf{\hat{j}}\Omega_0 u'_x] + \rho \mathbf{\hat{i}}\cdot[ \mathbf{\hat{i}}\Omega_0^2 x + \mathbf{\hat{j}}\Omega_0^2 y] \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u'_x)}{\partial t} + \nabla\cdot [(\rho u'_x)\mathbf{u'}] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{i}}\cdot\nabla P - \rho \mathbf{\hat{i}}\cdot\nabla \Phi + 2\rho \Omega_0 u'_y + \rho \Omega_0^2 x \, ; </math> |
|
<math>\mathbf{\hat{j}}:</math> |
<math> \frac{d(\rho u'_y)}{dt} + (\rho u'_y)\nabla\cdot \mathbf{u'} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{j}}\cdot\nabla P - \rho \mathbf{\hat{j}}\cdot\nabla \Phi + 2\rho \mathbf{\hat{j}}\cdot[\mathbf{\hat{i}}\Omega_0 u'_y - \mathbf{\hat{j}}\Omega_0 u'_x] + \rho \mathbf{\hat{j}}\cdot[ \mathbf{\hat{i}}\Omega_0^2 x + \mathbf{\hat{j}}\Omega_0^2 y] \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u'_y)}{\partial t} + \nabla\cdot [(\rho u'_y) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{j}}\cdot\nabla P - \rho \mathbf{\hat{j}}\cdot\nabla \Phi - 2\rho \Omega_0 u'_x + \rho \Omega_0^2 y \, ; </math> |
|
<math>\mathbf{\hat{k}}:</math> |
<math> \frac{d(\rho u'_z)}{dt} + (\rho u'_z)\nabla\cdot \mathbf{u'} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}}\cdot\nabla P - \rho \mathbf{\hat{k}}\cdot\nabla \Phi + 2\rho \mathbf{\hat{k}}\cdot[\mathbf{\hat{i}}\Omega_0 u'_y - \mathbf{\hat{j}}\Omega_0 u'_x] + \rho \mathbf{\hat{k}}\cdot[ \mathbf{\hat{i}}\Omega_0^2 x + \mathbf{\hat{j}}\Omega_0^2 y] \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u'_z)}{\partial t} + \nabla\cdot[(\rho u'_z) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}}\cdot\nabla P - \rho \mathbf{\hat{k}}\cdot\nabla \Phi \, . </math> |
In deriving these expressions, we also (a) have recognized from the start that, when expressed in Cartesian coordinates,
|
<math> ~{\vec{\Omega}}_f \times \vec{x} </math> |
<math>~=~</math> |
<math> {\hat\mathbf{k}} \Omega_0\times (\mathbf{\hat{i}}x + \mathbf{\hat{j}}y + \mathbf{\hat{k}}z) = - \mathbf{\hat{i}}\Omega_0 y + \mathbf{\hat{j}}\Omega_0 x \, , </math> |
|
<math> {\vec{\Omega}}_f \times ({\vec{\Omega}}_f \times \vec{x}) </math> |
<math>~=~</math> |
<math> \hat{\mathbf{k}} \Omega_0 \times ( - \mathbf{\hat{i}}\Omega_0 y + \mathbf{\hat{j}}\Omega_0 x ) = - \mathbf{\hat{i}}\Omega_0^2 x - \mathbf{\hat{j}}\Omega_0^2 y \, , </math> |
|
<math> {\vec{\Omega}}_f \times {\mathbf{u'}} </math> |
<math>~=~</math> |
<math> {\hat\mathbf{k}} \Omega_0\times (\mathbf{\hat{i}}u'_x + \mathbf{\hat{j}}u'_y + \mathbf{\hat{k}}u'_z) = - \mathbf{\hat{i}}\Omega_0 u'_y + \mathbf{\hat{j}}\Omega_0 u'_x\, , </math> |
and (b) have used the familiar operator mapping,
<math>\frac{d}{dt} \rightarrow \frac{\partial}{\partial t} + \mathbf{u'}\cdot \nabla \, ,</math>
to shift from the total (Lagrangian) time derivative to the partial (Eulerian) time derivative, which is usually the more desirable representation for computational simulations.
Step 2
Next, throughout this set of scalar equations, we replace each component of <math>~\rho\mathbf{u'}</math> with the corresponding component of <math>~(\rho\mathbf{u} - \rho {\vec{\Omega}}_f \times \vec{x})</math>, that is, we perform the following mappings:
|
<math> ~\rho u'_x </math> |
<math>~\rightarrow~</math> |
<math> ~\rho (u_x +\Omega_0 y) \, , </math> |
|
<math> ~\rho u'_y </math> |
<math>~\rightarrow~</math> |
<math> ~\rho (u_y - \Omega_0 x) \, , </math> |
|
<math> ~\rho u'_z </math> |
<math>~\rightarrow~</math> |
<math> ~\rho u_z \, . </math> |
As a result, the first of the three "hybrid" momentum-component equations becomes,
|
<math> \frac{\partial [ \rho (u_x +\Omega_0 y) ] }{\partial t} + \nabla\cdot \{ [\rho (u_x +\Omega_0 y) ]\mathbf{u'}\} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{i}}\cdot\nabla P - \rho \mathbf{\hat{i}}\cdot\nabla \Phi + 2\rho \Omega_0 (u_y - \Omega_0 x) + \rho \Omega_0^2 x </math> |
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u_x) }{\partial t} + \nabla\cdot [(\rho u_x) \mathbf{u'} ] + \Omega_0 y\biggl[ \frac{\partial \rho }{\partial t} + \nabla\cdot ( \rho \mathbf{u'} ) \biggr] + ( \rho \mathbf{u'} )\cdot\nabla (\Omega_0 y) </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{i}}\cdot\nabla P - \rho \mathbf{\hat{i}}\cdot\nabla \Phi + 2\rho \Omega_0 u_y - \rho \Omega_0^2 x \, . </math> |
Referencing the continuity equation, the middle bracketed term on the left-hand side can be set to zero; and the last term on the left-hand side,
|
<math> ( \rho \mathbf{u'} )\cdot\nabla (\Omega_0 y) </math> |
<math>~=~</math> |
<math> \rho \Omega_0 u'_y = \rho\Omega_0(u_y - \Omega_0 x) \, , </math> |
can be combined with terms on the right-hand side — cutting the Coriolis term in half and canceling the centrifugal acceleration term — to give,
|
<math> \frac{\partial (\rho u_x) }{\partial t} + \nabla\cdot [(\rho u_x) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{i}}\cdot\nabla P - \rho \mathbf{\hat{i}}\cdot\nabla \Phi + \rho \Omega_0 u_y \, . </math> |
Following a similar sequence of steps, the other two "hybrid" momentum conservation relations become,
|
<math> \frac{\partial (\rho u_y) }{\partial t} + \nabla\cdot [(\rho u_y) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{j}}\cdot\nabla P - \rho \mathbf{\hat{j}}\cdot\nabla \Phi - \rho \Omega_0 u_x \, , </math> |
|
<math> \frac{\partial (\rho u_z) }{\partial t} + \nabla\cdot [(\rho u_z) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}}\cdot\nabla P - \rho \mathbf{\hat{k}}\cdot\nabla \Phi \, . </math> |
Step 3
Cartesian Grid: Assuming the numerical simulation will be conducted on a Cartesian coordinate mesh, the divergence (advection) term on the left-hand-side should be evaluated by breaking the transport velocity into its three Cartesian components,
<math>~\mathbf{u'} = (u'_x, u'_y, u'_z) \, ,</math>
and, on the right-hand-side, the projection of the spatial operators should be written in the familiar form,
<math>\mathbf{\hat{i}}\cdot\nabla \rightarrow \frac{\partial}{\partial x} \, ,</math> <math>\mathbf{\hat{j}}\cdot\nabla \rightarrow \frac{\partial}{\partial y} \, ,</math> <math>\mathbf{\hat{k}}\cdot\nabla \rightarrow \frac{\partial}{\partial z} \, .</math>
In summary, then, the relevant set of momentum conservation equations is,
|
Cartesian Components of the Inertial-Frame Momentum |
|||||||||
| |||||||||
|
This is the set of equations that has served as the foundation of the Cartesian simulations reported in Byerly, Adelstein-Lelbach, Tohline, & Marcello (2014). |
Cylindrical Grid: If, instead, the numerical simulation is to be conducted on a cylindrical coordinate mesh, the spatial operators on both sides of the component momentum equations should be broken down into their cylindrical-coordinate components. In concert with this, the divergence (advection) term on the left-hand-side should be evaluated by breaking the transport velocity into its three cylindrical components,
<math>~\mathbf{u'} = (u'_R, u'_\varphi, u'_z) \, .</math>
Furthermore, recognizing that, when written in cylindrical coordinates, the gradient operator is,
<math> \nabla = \mathbf{\hat{e}}_R \frac{\partial}{\partial R} + \mathbf{\hat{e}}_\varphi \frac{1}{R} \frac{\partial}{\partial \varphi} +\mathbf{\hat{e}}_z \frac{\partial}{\partial z} \, , </math>
and that the unit vectors in cylindrical coordinates can be related to their Cartesian counterparts via the mappings,
<math>\mathbf{\hat{e}}_R = \mathbf{\hat{i}} \cos\varphi + \mathbf{\hat{j}} \sin\varphi \, ,</math>
<math>\mathbf{\hat{e}}_\varphi = \mathbf{\hat{j}} \cos\varphi - \mathbf{\hat{i}} \sin\varphi \, ,</math>
<math>\mathbf{\hat{e}}_z = \mathbf{\hat{k}} \, ,</math>
the relevant projections of the gradient operator on the right-hand-sides of the governing equations should take the form,
|
<math> \mathbf{\hat{i}}\cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \cos\varphi \frac{\partial}{\partial R} - \frac{\sin\varphi}{R} \frac{\partial}{\partial \varphi}\biggr] \, , </math> |
|
<math> \mathbf{\hat{j}}\cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \sin\varphi \frac{\partial}{\partial R} + \frac{\cos\varphi}{R} \frac{\partial}{\partial \varphi}\biggr] \, , </math> |
|
<math> \mathbf{\hat{k}}\cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \frac{\partial}{\partial z} \, . </math> |
In summary, then, the relevant set of momentum conservation equations is,
|
Cartesian Components of the Inertial-Frame Momentum |
|||||||||
|
Focus on Tracking Angular Momentum
Step 1
If the focus is on tracking angular momentum, then we need to break the vector momentum equation into its <math>(\mathbf\hat{e}_R, \mathbf\hat{e}_\varphi, \mathbf\hat{k})</math> components. As before, this is done by "dotting" each unit vector into the vector equation. This is less straightforward than in the Cartesian case because the orientation of both the <math>\mathbf\hat{e}_R</math> and <math>\mathbf\hat{e}_\varphi</math> unit vectors vary in space. As a result, the first term in the vector equation — the material time derivative — generates a couple of extra terms, viz.,
|
<math> \frac{d(\rho\mathbf{u'})}{dt} </math> |
<math>~=~</math> |
<math> \frac{d}{dt} [ \mathbf{\hat{e}}_R (\rho u'_R) + \mathbf{\hat{e}}_\varphi (\rho u'_\varphi) + \mathbf{\hat{k}} (\rho u'_z) ] </math> |
|
|
<math>~=~</math> |
<math> \mathbf{\hat{e}}_R \frac{d(\rho u'_R)}{dt} + \mathbf{\hat{e}}_\varphi \frac{d(\rho u'_\varphi)}{dt} + \mathbf{\hat{k}} \frac{d(\rho u'_z)}{dt} + (\rho u'_R) \frac{d}{dt}\mathbf{\hat{e}}_R + (\rho u'_\varphi) \frac{d}{dt}\mathbf{\hat{e}}_\varphi \, , </math> |
|
|
<math>~=~</math> |
<math> \mathbf{\hat{e}}_R \frac{d(\rho u'_R)}{dt} + \mathbf{\hat{e}}_\varphi \frac{d(\rho u'_\varphi)}{dt} + \mathbf{\hat{k}} \frac{d(\rho u'_z)}{dt} + \mathbf{\hat{e}}_\varphi(\rho u'_R) \frac{u'_\varphi}{R} - \mathbf{\hat{e}}_R(\rho u'_\varphi) \frac{u'_\varphi}{R} \, . </math> |
We also recognize that, when expressed in cylindrical coordinates,
|
<math> ~{\vec{\Omega}}_f \times \vec{x} </math> |
<math>~=~</math> |
<math> {\hat\mathbf{k}} \Omega_0\times (\mathbf{\hat{e}}_R R + \mathbf{\hat{k}}z) = \mathbf{\hat{e}}_\varphi \Omega_0 R \, , </math> |
|
<math> {\vec{\Omega}}_f \times ({\vec{\Omega}}_f \times \vec{x}) </math> |
<math>~=~</math> |
<math> \hat{\mathbf{k}} \Omega_0 \times ( \mathbf{\hat{e}}_\varphi \Omega_0 R ) = - \mathbf{\hat{e}}_R \Omega_0^2 R \, , </math> |
|
<math> {\vec{\Omega}}_f \times {\mathbf{u'}} </math> |
<math>~=~</math> |
<math> {\hat\mathbf{k}} \Omega_0\times (\mathbf{\hat{e}}_R u'_R + \mathbf{\hat{e}}_\varphi u'_\varphi + \mathbf{\hat{k}}u'_z) = \mathbf{\hat{e}}_\varphi \Omega_0 u'_R - \mathbf{\hat{e}}_R \Omega_0 u'_\varphi \, . </math> |
Hence, the process of "dotting" each unit vector into the equation leads to the following set of scalar momentum-component equations:
|
<math>\mathbf{\hat{e}}_R:</math> |
<math> \frac{d(\rho u'_R)}{dt} + (\rho u'_R)\nabla\cdot \mathbf{u'} - (\rho u'_\varphi) \frac{u'_\varphi}{R} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_R \cdot\nabla P - \rho \mathbf{\hat{e}}_R \cdot\nabla \Phi - 2\rho \mathbf{\hat{e}}_R \cdot [ \mathbf{\hat{e}}_\varphi \Omega_0 u'_R - \mathbf{\hat{e}}_R \Omega_0 u'_\varphi ] + \rho \mathbf{\hat{e}}_R\cdot (\mathbf{\hat{e}}_R \Omega_0^2 R) \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u'_R)}{\partial t} + \nabla\cdot [(\rho u'_R)\mathbf{u'}] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_R \cdot\nabla P - \rho \mathbf{\hat{e}}_R \cdot\nabla \Phi + \frac{\rho}{R} \biggl[ (u'_\varphi)^2 + 2R\Omega_0 u'_\varphi + (\Omega_0 R)^2 \biggr] \, </math> |
|
|
|
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_R \cdot\nabla P - \rho \mathbf{\hat{e}}_R \cdot\nabla \Phi + \frac{\rho}{R} (u'_\varphi + R\Omega_0)^2 \, ; </math> |
|
<math>\mathbf{\hat{e}}_\varphi:</math> |
<math> \frac{d(\rho u'_\varphi)}{dt} + (\rho u'_\varphi)\nabla\cdot \mathbf{u'} + (\rho u'_R) \frac{u'_\varphi}{R} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot\nabla \Phi - 2\rho \mathbf{\hat{e}}_\varphi \cdot [ \mathbf{\hat{e}}_\varphi \Omega_0 u'_R - \mathbf{\hat{e}}_R \Omega_0 u'_\varphi ] + \rho \mathbf{\hat{e}}_\varphi\cdot (\mathbf{\hat{e}}_R \Omega_0^2 R) \, </math> |
|
(mult. thru by R) |
<math> \Rightarrow ~~~~~ \frac{d(\rho R u'_\varphi)}{dt} + (\rho R u'_\varphi)\nabla\cdot \mathbf{u'} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot R\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot R \nabla \Phi - 2\rho R \Omega_0 u'_R \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho R u'_\varphi)}{\partial t} + \nabla\cdot [(\rho R u'_\varphi) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot R\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot R \nabla \Phi - 2\rho R \Omega_0 u'_R \, ; </math> |
|
<math>\mathbf{\hat{k}}:</math> |
<math> \frac{d(\rho u'_z)}{dt} + (\rho u'_z)\nabla\cdot \mathbf{u'} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}} \cdot\nabla P - \rho \mathbf{\hat{k}} \cdot\nabla \Phi - 2\rho \mathbf{\hat{k}} \cdot [ \mathbf{\hat{e}}_\varphi \Omega_0 u'_R - \mathbf{\hat{e}}_R \Omega_0 u'_\varphi ] + \rho \mathbf{\hat{k}}\cdot (\mathbf{\hat{e}}_R \Omega_0^2 R) \, </math> |
|
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho u'_z)}{\partial t} + \nabla\cdot[(\rho u'_z) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}}\cdot\nabla P - \rho \mathbf{\hat{k}}\cdot\nabla \Phi \, . </math> |
ASIDE: If we pause our discussion here and map this set of component equations onto a (rotating) cylindrical coordinate mesh — that is, if on the right-hand-sides we implement the straightforward operator projections,
<math>\mathbf{\hat{e}}_R \cdot\nabla \rightarrow \frac{\partial}{\partial R} \, ,</math> <math>\mathbf{\hat{e}}_\varphi \cdot\nabla \rightarrow \frac{1}{R} \frac{\partial}{\partial \varphi} \, ,</math> <math>\mathbf{\hat{k}}\cdot\nabla \rightarrow \frac{\partial}{\partial z} \, ,</math>
we obtain a formulation that is familiar to the astrophysics community. For example, as the following table of equations illustrates, it is the component set that has been spelled out in equations (5) - (7) of Norman & Wilson (1978) and equations (11), (12), & (3) of New & Tohline (1997).
|
Cylindrical Components of the Rotating-Frame Momentum |
|||||||||
|
|
Paragraph extracted without modification from p. 499 of M. L. Norman & J. R. Wilson (1978)
"The Fragmentation of Isothermal Rings and Star Formation"
ApJ, vol. 224, pp. 497-511 © American Astronomical Society |
|
Note: For complete correspondence with equations derived herein, set <math>(\gamma-1)E \rightarrow P</math> in all three component equations. |
|
Equations extracted† from K. C. B. New & J. E. Tohline (1997)
"The Relative Stability Against Merger of Close, Compact Binaries"
ApJ, vol. 490, pp. 311-327 © American Astronomical Society |
|
†Mathematical expressions displayed here, as a single digital image, with presentation order & layout modified from the original publication.
Note: When comparing this set of equations to the set presented by Norman & Wilson (1978), the definitions of the variables, <math>~\mathcal{S}</math> and <math>~\mathcal{T}</math>, must be swapped. |
[Comment by J. E. Tohline (April 7, 2014)] This is the set of equations that my research group has been using to simulate a wide variety of astrophysical fluid flows over the past twenty years. This is no longer our method of choice, however. A numerical algorithm based on the hybrid scheme, as summarized below, is far preferable to an algorithm that is based on this more familiar, traditional set of equations for several reasons:
- In the hybrid scheme, the Coriolis term disappears from the source term, so it is much easier to design and implement a computational algorithm that conserves angular momentum conservation.
- Although the hybrid scheme advects inertial-frame angular momentum, it retains all of the advantages associated with using a rotating frame of reference; for example, numerical diffusion is less severe and, in general, the Courant-limited time-step is larger than would be the case if you were forced to transport fluid in the inertial frame of reference.
- The hybrid scheme facilitates transport (and conservation) of angular momentum across a (rotating) Cartesian mesh. This facilitates the use of adaptive-mesh refinement (AMR) techniques and simplifies load-balancing on distributed memory, high-performance computers.
Step 2
Next, throughout this set of scalar equations, we replace each component of <math>~\rho\mathbf{u'}</math> with the corresponding component of <math>~(\rho\mathbf{u} - \rho {\vec{\Omega}}_f \times \vec{x})</math><math>= (\rho\mathbf{u} -\mathbf{\hat{e}}_\varphi \rho R\Omega_0)</math>, that is, we perform the following mappings:
|
<math> ~\rho u'_R </math> |
<math>~\rightarrow~</math> |
<math> ~\rho u_R \, , </math> |
|
<math> ~\rho u'_\varphi </math> |
<math>~\rightarrow~</math> |
<math> ~\rho (u_\varphi - R\Omega_0 ) \, , </math> |
|
<math> ~\rho u'_z </math> |
<math>~\rightarrow~</math> |
<math> ~\rho u_z \, . </math> |
As a result, the first and third of the three "hybrid" momentum-component equations become, respectively,
|
<math>\mathbf{\hat{e}}_R:</math> |
<math> \frac{\partial (\rho u_R)}{\partial t} + \nabla\cdot [(\rho u_R)\mathbf{u'}] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_R \cdot\nabla P - \rho \mathbf{\hat{e}}_R \cdot\nabla \Phi + \frac{\rho u^2_\varphi}{R} \, ; </math> |
|
<math>\mathbf{\hat{k}}:</math> |
<math> \frac{\partial (\rho u_z) }{\partial t} + \nabla\cdot [(\rho u_z) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{k}}\cdot\nabla P - \rho \mathbf{\hat{k}}\cdot\nabla \Phi \, . </math> |
The second of the three "hybrid" momentum component equations — the one governing conservation of angular momentum — becomes,
|
<math> \frac{\partial [\rho R (u_\varphi - R\Omega_0 ) ]}{\partial t} + \nabla\cdot \{ [\rho R (u_\varphi - R\Omega_0 ) ] \mathbf{u'} \} </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot R\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot R \nabla \Phi - 2\rho R \Omega_0 u_R \, </math> |
|
<math> \Rightarrow ~~~~~ \frac{\partial (\rho R u_\varphi) }{\partial t} + \nabla\cdot [(\rho R u_\varphi) \mathbf{u'} ] - R^2 \Omega_0 \biggl[ \frac{\partial \rho }{\partial t} + \nabla\cdot ( \rho \mathbf{u'} ) \biggr] - ( \rho \mathbf{u'} )\cdot\nabla (R^2 \Omega_0) </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot R\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot R \nabla \Phi - 2\rho R \Omega_0 u_R \, . </math> |
Referencing the continuity equation, as before, the middle bracketed term on the left-hand side can be set to zero; and the last term on the left-hand side,
|
<math> ( \rho \mathbf{u'} )\cdot\nabla (R^2\Omega_0) </math> |
<math>~=~</math> |
<math> 2\rho R \Omega_0 u_R \, , </math> |
matches and, hence, exactly cancels the Coriolis term on the right-hand side to give,
|
<math>\mathbf{\hat{e}}_\varphi:</math> |
<math> \frac{\partial (\rho R u_\varphi) }{\partial t} + \nabla\cdot [(\rho R u_\varphi) \mathbf{u'} ] </math> |
<math>~=~</math> |
<math> - \mathbf{\hat{e}}_\varphi \cdot R\nabla P - \rho \mathbf{\hat{e}}_\varphi \cdot R \nabla \Phi \, . </math> |
Step 3
Cylindrical Grid: If the numerical simulation is to be conducted on a cylindrical coordinate mesh, the spatial operators on both sides of the component momentum equations should be broken down into their cylindrical-coordinate components. That is, as in the above "ASIDE," the appropriate operator projections on the right-hand-sides of the equations are,
<math>\mathbf{\hat{e}}_R \cdot\nabla \rightarrow \frac{\partial}{\partial R} \, ,</math> <math>\mathbf{\hat{e}}_\varphi \cdot\nabla \rightarrow \frac{1}{R} \frac{\partial}{\partial \varphi} \, ,</math> <math>\mathbf{\hat{k}}\cdot\nabla \rightarrow \frac{\partial}{\partial z} \, .</math>
In concert with this, the divergence (advection) term on the left-hand-side should be evaluated by breaking the transport velocity into its three cylindrical components,
<math>~\mathbf{u'} = (u'_R, u'_\varphi, u'_z) \, .</math>
The relevant set of momentum conservation equations is, therefore,
|
Cylindrical Components of the Inertial-Frame Momentum |
|||||||||
|
Cartesian Grid: If, instead, the numerical simulation is to be conducted on a Cartesian coordinate mesh, the spatial operators on both sides of the component momentum equations should be broken down into their Cartesian-coordinate components. In concert with this, the divergence (advection) term on the left-hand-side should be evaluated by breaking the transport velocity into its three Cartesian components,
<math>~\mathbf{u'} = (u'_x, u'_y, u'_z) \, .</math>
Furthermore, recognizing that, when written in Cartesian coordinates, the gradient operator is,
<math> \nabla = \mathbf{\hat{i}} \frac{\partial}{\partial x} + \mathbf{\hat{j}} \frac{\partial}{\partial y} +\mathbf{\hat{k}} \frac{\partial}{\partial z} \, , </math>
and that the unit vectors in Cartesian coordinates can be related to their cylindrical counterparts via the mappings,
<math>\mathbf{\hat{i}} = \mathbf{\hat{e}}_R \cos\varphi - \mathbf{\hat{e}}_\varphi \sin\varphi \, ,</math>
<math>\mathbf{\hat{j}} = \mathbf{\hat{e}}_R \sin\varphi + \mathbf{\hat{e}}_\varphi \cos\varphi \, ,</math>
<math>\mathbf{\hat{k}} = \mathbf{\hat{k}} \, ,</math>
the relevant projections of the gradient operator on the right-hand-sides of the governing equations should take the form,
|
<math> \mathbf{\hat{e}}_R \cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \cos\varphi \frac{\partial}{\partial x} +\sin\varphi \frac{\partial}{\partial y} \biggr] = \biggl[ \frac{x}{(x^2+y^2)^{1/2}} \frac{\partial}{\partial x} +\frac{y}{(x^2+y^2)^{1/2}} \frac{\partial}{\partial y} \biggr] \, , </math> |
|
<math> R\mathbf{\hat{e}}_\varphi \cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \biggl[ - R\sin\varphi \frac{\partial}{\partial x} +R\cos\varphi \frac{\partial}{\partial y} \biggr] = \biggl[ - y \frac{\partial}{\partial x} +x \frac{\partial}{\partial y} \biggr] \, , </math> |
|
<math> \mathbf{\hat{k}}\cdot\nabla </math> |
<math>~\rightarrow~</math> |
<math> \frac{\partial}{\partial z} \, . </math> |
In summary, then, the relevant set of momentum conservation equations is,
|
Cylindrical Components of the Inertial-Frame Momentum |
|||||||||
| |||||||||
|
This is the set of equations that has served as the foundation of the so-called Hybrid simulations reported in Byerly, Adelstein-Lelbach, Tohline, & Marcello (2014). |
Related Discussions
- Jay Call's dissertation at LSU
- Euler equation viewed from a rotating frame of reference, or Main Page.
- An earlier draft of this "Euler equation" presentation.
- Early draft of Hybrid Scheme discussion: Appendix/Ramblings/Hybrid Scheme Old

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |