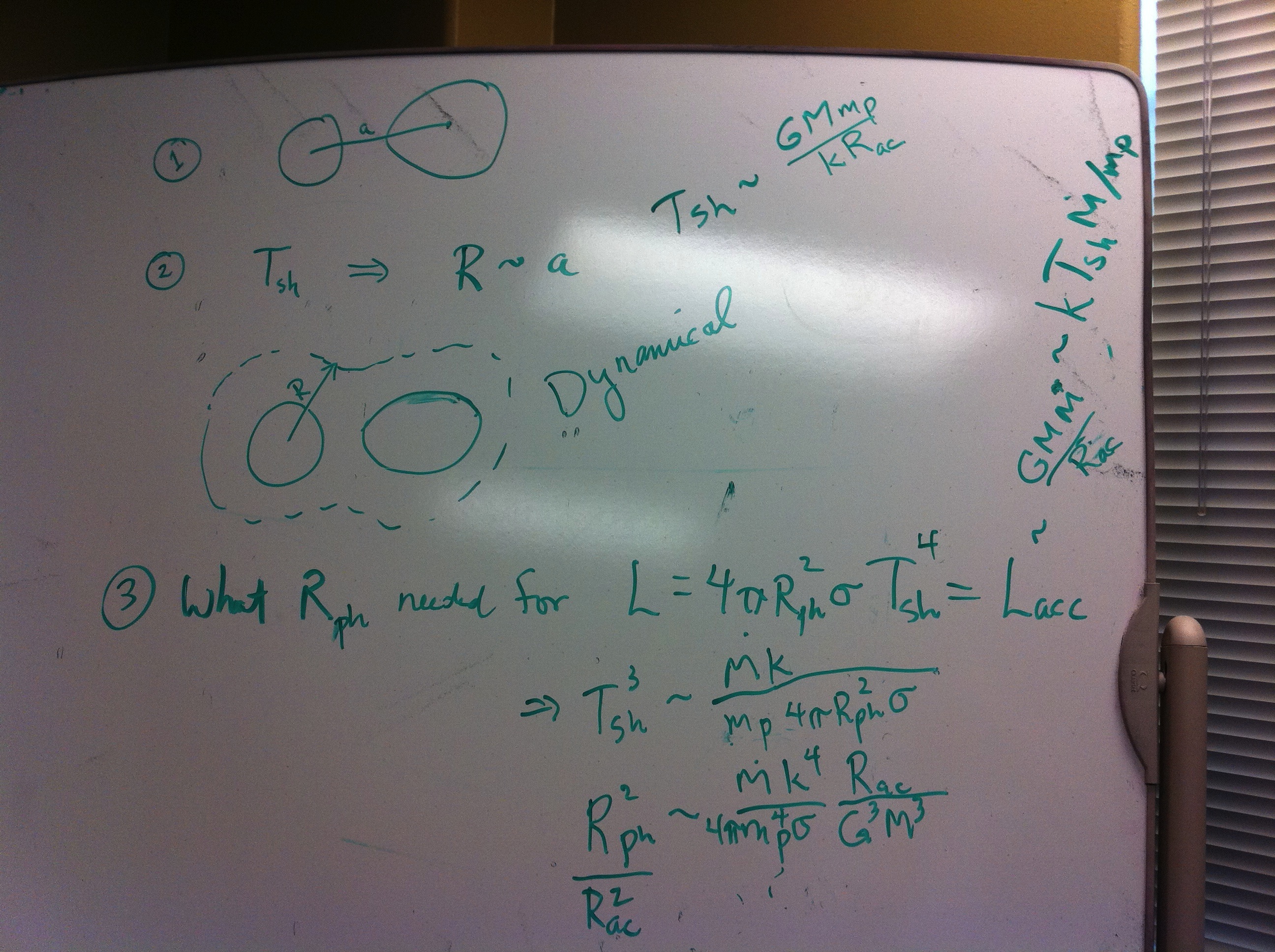User:Tohline/Appendix/Ramblings/Photosphere

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Locating the Photosphere of Stably Accreting Double White Dwarf Binaries
Context
At our regularly scheduled astrophysics group meeting on Monday, 2 May 2011, Juhan Frank and I started debating the answer to the following question: What should the photospheric radius be of the common envelope that surrounds a stably accreting, double white dwarf (DWD) binary? That is, does an accreting DWD binary that is destined to be an AM CVn system look like a single bloated star? The various mathematical relations that we think are relevant to this question were sketched on the whiteboard in room 218 Johnston Hall (CCT). Here is a photo of that whiteboard discussion and derivation.
Initial Derivation
As the accretion stream from the less massive white dwarf impacts the surface of the accretor supersonically, it will heat the accreted material to a post-shock temperature,
<math>T_{sh} \approx \frac{GM_a m_p}{kR_a}\cdot f</math> ,
where <math>M_a</math> and <math>R_a</math> are the mass and radius, respectively, of the accretor, and 0 < f ≤ 1 is a coefficient signifying the fraction of potential energy that is converted into heat. Assuming the post-shock material is optically thick to photon radiation, we should ask to what "photospheric" radius, <math>R_{ph}</math>, the envelope of the accretor will have to swell in order for the star (in steady state) to be able to radiate all of the accretion energy? It seems that it will need,
<math> 4\pi R_{ph}^2 \sigma T_{sh}^4 = L_{acc} </math>
<math> \Rightarrow~~~~~\biggl[ \frac{R_{ph}}{R_a} \biggr]^2 = \frac{L_{acc}}{\pi a_{rad}c R_a^2 T^4_{sh}} = \frac{GM_a \dot{M}}{\pi a_{rad}c R_a^3 T^4_{sh}} \, , </math>
where we've set <math>4\sigma = a_{rad}c</math> and,
<math> L_{acc} = \frac{GM_a \dot{M}}{R_a} \, . </math>
Replacing <math>T_{sh}</math> by the approximate expression shown above gives,
<math> \biggl[ \frac{R_{ph}}{R_a} \biggr]^2 \approx \frac{GM_a \dot{M}}{\pi a_{rad}c R_a^3} \biggl[ \frac{kR_a}{GM_a m_p} \biggr]^4 f^{-4} = \biggl[ \frac{15(hc)^3}{8\pi^5 k^4} \biggr] \frac{R_a \dot{M}}{\pi c G^3 M_a^3} \biggl[ \frac{k}{ m_p} \biggr]^4 f^{-4} = \biggl[ \frac{15}{8\pi^5} \biggr] \frac{R_a \dot{M}}{\pi c m_p^4} \biggl[ \frac{hc}{ GM_a} \biggr]^3 f^{-4} \, . </math>
We recognize that the combination of physical constants in this expression resemble the Chandrasekhar Mass, <math>M_{Ch}</math>. Specifically,
<math> \frac{c^3 h^3}{G^3 m_p^4} = \frac{2^5 \pi^2}{3 m_3^2} [ \mu_e^2 M_\mathrm{Ch} ]^2. </math>
Hence,
<math> \frac{R_{ph}}{R_a} \approx \biggl[ \frac{20}{\pi^4} \biggr]^{1/2} \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr] \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{1/2} f^{-2} \, . </math>
Because <math>R_a/c</math> is less than 1 second for white dwarfs, we see that <math>R_{ph}/R_a \ll 1</math> unless <math>\dot{M}/M_a</math> is very large or <math>f</math> is very small. This does not make physical sense. The result is probably screwy because we've incorrectly assumed that the temperature of the common envelope is approximately <math>T_{sh}</math>.
Better Temperature Estimate
Now let's assume that the common envelope puffs up adiabatically, in which case the temperature of the photosphere (and envelope) should be,
<math>T_{ph} \approx T_{sh} \biggl( \frac{\rho_{ph}} {\rho_{sh}} \biggr)^{\gamma - 1} \approx T_{sh} \biggl( \frac{R_{ph}} {R_a} \biggr)^{3(1-\gamma)}</math> .
So, by analogy with the above initial derivation, if we demand that,
<math> 4\pi R_{ph}^2 \sigma T_{ph}^4 = L_{acc} \, , </math>
then,
<math> \biggl[ \frac{R_{ph}}{R_a} \biggr]^2 = \frac{L_{acc}}{\pi a_{rad}c R_a^2 T^4_{sh}} \biggl[\frac{R_{ph}}{R_a} \biggr]^{12(\gamma-1)} \approx \biggl[ \frac{20}{\pi^4} \biggr] \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr]^2 \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr] f^{-4} \biggl[\frac{R_{ph}}{R_a} \biggr]^{12(\gamma-1)} </math>
<math> \Rightarrow~~~~~ \biggl[ \frac{R_{ph}}{R_a} \biggr]^{2(6\gamma - 7)} \approx \biggl[ \frac{20}{\pi^4} \biggr]^{-1} \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr]^{-2} \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{-1} f^{4} </math>
<math> \Rightarrow~~~~~ \frac{R_{ph}}{R_a} \approx \biggl\{ \biggl[ \frac{20}{\pi^4} \biggr]^{-1} \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr]^{-2} \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{-1} f^{4} \biggr\}^{1/[2(6\gamma-7)]} \, . </math>
Hence, for a <math>\gamma=5/3</math> envelope,
<math> \frac{R_{ph}}{R_a} \approx \biggl\{ \biggl[ \frac{20}{\pi^4} \biggr]^{-1} \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr]^{-2} \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{-1} f^{4} \biggr\}^{1/6} \, . </math>
Now, based on the accompanying discussion of the Chandrasekhar mass,
<math>\frac{ m_3 M_\odot}{\mu_e^2 M_{Ch}}=0.353 \, .</math>
Hence,
<math> \frac{R_{ph}}{R_a} \approx 0.920 \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{-1/6} f^{2/3} \approx \biggl[ \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c } \biggr]^{-1/6} \, . </math>
This relation behaves in a very different way from the initially derived relation. For small mass-transfer rates, this relation predicts that the photospheric radius will be quite large relative to the radius of the accretor.
Derivation from Juhan Frank
In his independent derivation, Juhan substitutes the following dimensionless mass-transfer rate:
<math> \dot{m} \equiv \frac{\dot{M}}{\dot{M}_{int}} = \frac{\kappa\dot{M}}{4\pi c R_a} \, , </math>
where, <math>\kappa = \sigma_T/m_p</math>. Hence,
<math> \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c} = \dot{m} \biggl[ \frac{4\pi R_a^2}{\kappa M_a} \biggr] \, , </math>
and,
<math> \frac{R_{ph}}{R_a} \approx \biggl\{ \biggl[ \frac{20}{\pi^4} \biggr]^{-1} \biggl[ \frac{\mu_e^2 M_{Ch}}{ m_3 M_a} \biggr]^{-2} \biggl[ \frac{4\pi R_a^2}{\kappa M_a} \biggr]^{-1} {\dot{m}}^{-1} f^{4} \biggr\}^{1/6} =
\biggl\{
\biggl[ \frac{\pi^4}{20} \biggr] \biggl[ \frac{ m_3 M_\odot}{\mu_e^2 M_{Ch}} \biggr]^{2} \biggl[ \frac{\kappa M_\odot}{4\pi R_9^2 } \biggr] \biggr\}^{1/6} \biggl[ \frac{f^{2/3}}{\dot{m}^{1/6}} \biggl( \frac{M_a}{M_\odot} \biggr)^{1/2} \biggl( \frac{R_9 }{R_a} \biggr) ^{1/3}\biggr] \, , </math>
where <math>R_9 \equiv 10^9~\mathrm{cm}</math>. Again, since,
<math>\frac{ m_3 M_\odot}{\mu_e^2 M_{Ch}}=0.353 \, ,</math>
we obtain,
<math> \frac{R_{ph}}{R_a} = 183.9 \biggl[ \frac{f^{2/3}}{\dot{m}^{1/6}} \biggl( \frac{M_a}{M_\odot} \biggr)^{1/2} \biggl( \frac{R_9 }{R_a} \biggr) ^{1/3}\biggr] \, . </math>
Mass-Transfer Rates
Juhan chose the situation where everything inside the final square brackets is unity, in which case,
<math> f = 1; ~ \dot{m} = 1; ~ M_a = 1M_\odot; ~ R_a = 10^9\mathrm{cm}; ~ \mathrm{and}~ R_{ph} \approx 2.63 R_\odot \, . </math>
If I use the same values, I get,
<math> \frac{\dot{M}}{M_a} \cdot \frac{R_a}{c} = \dot{m} \biggl[ \frac{4\pi R_a^2}{\kappa M_a} \biggr] = 1.57\times 10^{-14} \, . </math>
This means,
<math> \frac{\dot{M}}{M_a} = 4.7\times 10^{-13} ~\mathrm{s}^{-1} \approx 1.5\times 10^{-5} ~\mathrm{yr}^{-1} \, . </math>
According to Kopparapu & Tohline (2007) (hereafter, KT07), the mass-transfer rate for stable, mass-transferring double-white dwarfs is,
<math> \frac{\dot{M}}{M_a} \approx \tau_\mathrm{chirp}^{-1} \, . </math>
Combining these last two expressions means,
<math> \tau_\mathrm{chirp} \approx 2\times 10^{12}~ \mathrm{s} = 6.7\times 10^4~\mathrm{yr} \, . </math>

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |