User:Tohline/Appendix/Ramblings/ConcentricEllipsodalCoordinates
Concentric Ellipsoidal (T6) Coordinates

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Background
Building on our general introduction to Direction Cosines in the context of orthogonal curvilinear coordinate systems, and on our previous development of T3 (concentric oblate-spheroidal) and T5 (concentric elliptic) coordinate systems, here we explore the creation of a concentric ellipsoidal (T6) coordinate system. This is motivated by our desire to construct a fully analytically prescribable model of a nonuniform-density ellipsoidal configuration that is an analog to Riemann S-Type ellipsoids.
Orthogonal Coordinates
Primary (radial-like) Coordinate
We start by defining a "radial" coordinate whose values identify various concentric ellipsoidal shells,
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, .</math> |
When <math>~\lambda_1 = a</math>, we obtain the standard definition of an ellipsoidal surface, it being understood that, <math>~q^2 = a^2/b^2</math> and <math>~p^2 = a^2/c^2</math>. (We will assume that <math>~a > b > c</math>, that is, <math>~p^2 > q^2 > 1</math>.)
A vector, <math>~\bold{\hat{n}}</math>, that is normal to the <math>~\lambda_1</math> = constant surface is given by the gradient of the function,
|
<math>~F(x, y, z)</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} - \lambda_1 \, .</math> |
In Cartesian coordinates, this means,
|
<math>~\bold{\hat{n}}(x, y, z)</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl( \frac{\partial F}{\partial x} \biggr) + \hat\jmath \biggl( \frac{\partial F}{\partial y} \biggr) + \hat{k} \biggl( \frac{\partial F}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl[ x(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] + \hat\jmath \biggl[ q^2y(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] + \hat{k}\biggl[ p^2 z(x^2 + q^2 y^2 + p^2 z^2)^{- 1 / 2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl( \frac{x}{\lambda_1} \biggr) + \hat\jmath \biggl( \frac{q^2y}{\lambda_1} \biggr) + \hat{k}\biggl(\frac{p^2 z}{\lambda_1} \biggr) \, , </math> |
where it is understood that this expression is only to be evaluated at points, <math>~(x, y, z)</math>, that lie on the selected <math>~\lambda_1</math> surface — that is, at points for which the function, <math>~F(x,y,z) = 0</math>. The length of this normal vector is given by the expression,
|
<math>~[ \bold{\hat{n}} \cdot \bold{\hat{n}} ]^{1 / 2}</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{\partial F}{\partial x} \biggr)^2 + \biggl( \frac{\partial F}{\partial y} \biggr)^2 + \biggl( \frac{\partial F}{\partial z} \biggr)^2 \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{x}{\lambda_1} \biggr)^2 + \biggl( \frac{q^2y}{\lambda_1} \biggr)^2 + \biggl(\frac{p^2 z}{\lambda_1} \biggr)^2 \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\lambda_1 \ell_{3D}} </math> |
where,
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, .</math> |
It is therefore clear that the properly normalized normal unit vector that should be associated with any <math>~\lambda_1</math> = constant ellipsoidal surface is,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \frac{ \bold\hat{n} }{ [ \bold{\hat{n}} \cdot \bold{\hat{n}} ]^{1 / 2} } = \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, . </math> |
From our accompanying discussion of direction cosines, it is clear, as well, that the scale factor associated with the <math>~\lambda_1</math> coordinate is,
|
<math>~h_1^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 \ell_{3D}^2 \, .</math> |
We can also fill in the top line of our direction-cosines table, namely,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
|
|
|
| <math>~3</math> |
|
|
|
Other Coordinate Pair in the Tangent Plane
Let's focus on a particular point on the <math>~\lambda_1</math> = constant surface, <math>~(x_0, y_0, z_0)</math>, that necessarily satisfies the function, <math>~F(x_0, y_0, z_0) = 0</math>. We have already derived the expression for the unit vector that is normal to the ellipsoidal surface at this point, namely,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \hat\imath (x_0 \ell_{3D}) + \hat\jmath (q^2y_0 \ell_{3D}) + \hat\jmath (p^2 z_0 \ell_{3D}) \, , </math> |
where, for this specific point on the surface,
|
<math>~\ell_{3D}</math> |
<math>~=</math> |
<math>~\biggl[ x_0^2 + q^4y_0^2 + p^4 z_0^2 \biggr]^{- 1 / 2} \, .</math> |
|
Tangent Plane The two-dimensional plane that is tangent to the <math>~\lambda_1</math> = constant surface at this point is given by the expression,
|
Fix the value of <math>~\lambda_1</math>. This means that the relevant ellipsoidal surface is defined by the expression,
|
<math>~\lambda_1^2</math> |
<math>~=</math> |
<math>~x^2 + q^2y^2 + p^2z^2 \, .</math> |
If <math>~z = 0</math>, the semi-major axis of the relevant x-y ellipse is <math>~\lambda_1</math>, and the square of the semi-minor axis is <math>~\lambda_1^2/q^2</math>. At any other value, <math>~z = z_0 < c</math>, the square of the semi-major axis of the relevant x-y ellipse is, <math>~(\lambda_1^2 - p^2z_0^2)</math> and the square of the corresponding semi-minor axis is, <math>~(\lambda_1^2 - p^2z_0^2)/q^2</math>. Now, for any chosen <math>~x_0^2 \le (\lambda_1^2 - p^2z_0^2)</math>, the y-coordinate of the point on the <math>~\lambda_1</math> surface is given by the expression,
|
<math>~y_0^2</math> |
<math>~=</math> |
<math>~\frac{1}{q^2}\biggl[ \lambda_1^2 - p^2 z_0 -x_0^2 \biggr] \, .</math> |
The slope of the line that lies in the z = z0 plane and that is tangent to the ellipsoidal surface at <math>~(x_0, y_0)</math> is,
|
<math>~m \equiv \frac{dy}{dx}\biggr|_{z_0}</math> |
<math>~=</math> |
<math>~- \frac{x_0}{q^2y_0}</math> |
Speculation1
Building on our experience developing T3 Coordinates and, more recently, T5 Coordinates, let's define the two "angles,"
|
<math>~\Zeta</math> |
<math>~\equiv</math> |
<math>~\sinh^{-1}\biggl(\frac{qy}{x} \biggr)</math> |
and, |
<math>~\Upsilon</math> |
<math>~\equiv</math> |
<math>~\sinh^{-1}\biggl(\frac{pz}{x} \biggr) \, ,</math> |
in which case we can write,
|
<math>~\lambda_1^2</math> |
<math>~=</math> |
<math>~x^2(\cosh^2\Zeta + \sinh^2\Upsilon)\, .</math> |
We speculate that the other two orthogonal coordinates may be defined by the expressions,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~x \biggl[ \sinh\Zeta \biggr]^{1/(1-q^2)} = x \biggl[ \frac{qy}{x}\biggr]^{1/(1-q^2)} = x \biggl[ \frac{x}{qy}\biggr]^{1/(q^2-1)} = \biggl[ \frac{x^{q^2}}{qy}\biggr]^{1/(q^2-1)} \, ,</math> |
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~x \biggl[ \sinh\Upsilon \biggr]^{1/(1-p^2)} = x \biggl[ \frac{pz}{x}\biggr]^{1/(1-p^2)} = x \biggl[ \frac{x}{pz}\biggr]^{1/(p^2-1)} = \biggl[ \frac{x^{p^2}}{pz}\biggr]^{1/(p^2-1)} \, .</math> |
Some relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{1}{qy}\biggr]^{1/(q^2-1)} \biggl[ \frac{q^2}{q^2-1} \biggr]x^{1/(q^2-1)} = \biggl[ \frac{q^2}{q^2-1} \biggr]\biggl[ \frac{x}{qy}\biggr]^{1/(q^2-1)} = \biggl[ \frac{q^2}{q^2-1} \biggr]\frac{\lambda_2}{x} \, ; </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{x^{q^2}}{q}\biggr]^{1/(q^2-1)} \biggl[ \frac{1}{1-q^2} \biggr] y^{q^2/(1-q^2)} = - \biggl[ \frac{1}{q^2-1} \biggr] \frac{\lambda_2}{y} \, ;</math> |
|
<math>~\frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{p^2}{p^2-1} \biggr]\frac{\lambda_3}{x} \, ; </math> |
|
<math>~\frac{\partial \lambda_3}{\partial z}</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{1}{p^2-1} \biggr] \frac{\lambda_3}{z} \, .</math> |
And the associated scale factors are,
|
<math>~h_2^2</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \biggl( \frac{q^2}{q^2-1} \biggr)\frac{\lambda_2}{x} \biggr]^2 + \biggl[ - \biggl( \frac{1}{q^2-1} \biggr) \frac{\lambda_2}{y} \biggr]^2 \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl( \frac{q^2}{q^2-1} \biggr)^2 \frac{\lambda_2^2}{x^2} + \biggl( \frac{1}{q^2-1} \biggr)^2 \frac{\lambda_2^2}{y^2} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{x^2 + q^4 y^2 \biggr\}^{-1} \biggl[ \frac{(q^2 - 1)^2x^2 y^2}{\lambda_2^2} \biggr] \, ; </math> |
|
<math>~h_3^2</math> |
<math>~=</math> |
<math>~ \biggl\{x^2 + p^4 z^2 \biggr\}^{-1} \biggl[ \frac{(p^2 - 1)^2x^2 z^2}{\lambda_3^2} \biggr] \, . </math> |
We can now fill in the rest of our direction-cosines table, namely,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
<math>~q^2 y \ell_q </math> |
<math>~-x\ell_q</math> |
<math>~0</math> |
| <math>~3</math> |
<math>~p^2 z \ell_p</math> |
<math>~0</math> |
<math>~-x\ell_p</math> |
Hence,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat\imath \gamma_{21} + \hat\jmath \gamma_{22} +\hat{k} \gamma_{23} = \hat\imath (q^2y\ell_q) - \hat\jmath (x\ell_q) \, ; </math> |
|
<math>~\hat{e}_3</math> |
<math>~=</math> |
<math>~ \hat\imath \gamma_{31} + \hat\jmath \gamma_{32} +\hat{k} \gamma_{33} = \hat\imath (p^2z\ell_p) -\hat{k} (x\ell_p) \, . </math> |
Check:
|
<math>~\hat{e}_2 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ (q^2y\ell_q)^2 + (x\ell_q)^2 = 1 \, ; </math> |
|
<math>~\hat{e}_3 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ (p^2z\ell_p)^2 + (x\ell_p)^2 = 1 \, ; </math> |
|
<math>~\hat{e}_2 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ (q^2y\ell_q)(p^2z\ell_p) \ne 0 \, . </math> |
Speculation2
Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x}{y^{1/q^2} z^{1/p^2}} \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_2}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{x}{z^{1/p^2}} \biggl(-\frac{1}{q^2}\biggr) y^{-1/q^2 - 1} = -\frac{\lambda_2}{q^2 y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ -\frac{\lambda_2}{p^2 z} \, . </math> |
The associated scale factor is, then,
|
<math>~h_2^2</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{ \lambda_2}{x} \biggr)^2 + \biggl( -\frac{\lambda_2}{q^2y} \biggr)^2 + \biggl( - \frac{\lambda_2}{p^2z} \biggr)^2 \biggr]^{-1} </math> |
Speculation3
Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{(x+p^2 z)^{1 / 2}}{y^{1/q^2} } \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{2y^{1/q^2}}\biggl(x + p^2z\biggr)^{- 1 / 2} = \frac{\lambda_2}{2(x + p^2z) } \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ -\frac{\lambda_2}{q^2y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \, . </math> |
Speculation4
Development
Here we stick with the primary (radial-like) coordinate as defined above; for example,
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ,</math> |
|
<math>~h_1</math> |
<math>~=</math> |
<math>~\lambda_1 \ell_{3D} \, ,</math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~[ x^2 + q^4y^2 + p^4 z^2 ]^{- 1 / 2} \, ,</math> |
|
<math>~\hat{e}_1 </math> |
<math>~=</math> |
<math>~ \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, . </math> |
|
Note that, <math>~\hat{e}_1 \cdot \hat{e}_1 = 1</math>, which means that this is, indeed, a properly normalized unit vector. |
Then, drawing from our earliest discussions of "T1 Coordinates", we'll try defining the second coordinate as,
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} u \, , </math> where, |
|
<math>~u</math> |
<math>~\equiv</math> |
<math>\frac{y^{1/q^2}}{x} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + u^2} \biggl[ - \frac{y^{1/q^2}}{x^2} \biggr] = - \biggl[ \frac{u}{1 + u^2}\biggr]\frac{1}{x} = - \frac{\sin\lambda_3 \cos\lambda_3}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_3}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + u^2} \biggl[ \frac{y^{(1/q^2-1)}}{q^2x} \biggr] = \biggl[ \frac{u}{1 + u^2}\biggr]\frac{1}{q^2y} = \frac{\sin\lambda_3 \cos\lambda_3}{q^2y} \, , </math> |
which means that,
|
<math>~h_3^2</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{\partial \lambda_3}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_3}{\partial y} \biggr)^2 \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{u}{1 + u^2}\biggr]^{-2} \biggl[ \frac{1}{x^2} + \frac{1}{q^4y^2} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1 + u^2}{u}\biggr]^{2} \biggl[ \frac{x^2 + q^4y^2}{x^2q^4y^2} \biggr]^{-1} </math> |
|
<math>~\Rightarrow~~~h_3</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{1 + u^2}{u}\biggr]xq^2 y \ell_q = \frac{xq^2 y \ell_q}{\sin\lambda_3 \cos\lambda_3} \, , </math> where, |
|
<math>~\ell_q</math> |
<math>~\equiv</math> |
<math>~[x^2 + q^4 y^2]^{-1 / 2} \, .</math> |
The third row of direction cosines can now be filled in to give,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
|
|
|
| <math>~3</math> |
<math>~-q^2 y \ell_q</math> |
<math>~x \ell_q</math> |
<math>~0</math> |
which means that the associated unit vector is,
|
<math>~\hat{e}_3 </math> |
<math>~=</math> |
<math>~ -\hat\imath (q^2 y \ell_{q}) + \hat\jmath (x \ell_{q}) \, . </math> |
|
Note that, <math>~\hat{e}_3 \cdot \hat{e}_3 = 1</math>, which means that this also is a properly normalized unit vector. Note, as well, that the dot product between our "first" and "third" unit vectors should be zero if they are indeed orthogonal to each other. Let's see …
Q.E.D. |
Now, even though we have not yet determined the proper expression for the "second" orthogonal coordinate, <math>~\lambda_2</math>, we should be able to obtain an expression for its associated unit vector from the cross product of the "third" and "first" unit vectors. Specifically we find,
|
<math>~\hat{e}_2 \equiv \hat{e}_3 \times \hat{e}_1</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl[ (e_3)_2 (e_1)_3 - (e_3)_3(e_1)_2 \biggr] + \hat\jmath \biggl[ (e_3)_3 (e_1)_1 - (e_3)_1(e_1)_3 \biggr] + \hat{k} \biggl[ (e_3)_1 (e_1)_2 - (e_3)_2(e_1)_1 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath \biggl[ (x \ell_q) (p^2 z \ell_{3D}) - 0 \biggr] + \hat\jmath \biggl[ 0 - (-q^2y \ell_q)(p^2z \ell_{3D}) \biggr] + \hat{k} \biggl[ (-q^2y \ell_q) (q^2 y \ell_{3D}) - (x\ell_q)(x\ell_{3D}) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\ell_q \ell_{3D}\biggl[ \hat\imath ( xp^2 z ) + \hat\jmath ( q^2y p^2z ) - \hat{k} ( x^2 + q^4 y^2 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\ell_q \ell_{3D}\biggl[ \hat\imath ( xp^2 z ) + \hat\jmath ( q^2y p^2z ) - \hat{k} \biggl( \frac{1}{\ell_q^2} \biggr) \biggr] \, . </math> |
|
Note that,
and,
We conclude, therefore, that <math>~\hat{e}_2</math> is perpendicular to both of the other unit vectors. Hooray! |
Filling in the second row of the direction cosines table gives,
|
Direction Cosines for T6 Coordinates
|
|||
| <math>~n</math> | <math>~i = x, y, z</math> | ||
| <math>~1</math> | <math>~x\ell_{3D}</math> | <math>~q^2 y \ell_{3D}</math> | <math>~p^2 z \ell_{3D}</math> |
| <math>~2</math> |
<math>~x p^2 z\ell_q \ell_{3D}</math> |
<math>~q^2y p^2 z\ell_q \ell_{3D}</math> |
<math>~-(x^2 + q^4y^2)\ell_q \ell_{3D} = - \ell_{3D}/\ell_q</math> |
| <math>~3</math> |
<math>~-q^2 y \ell_q</math> |
<math>~x \ell_q</math> |
<math>~0</math> |
Analysis
Let's break down each direction cosine into its components.
| Direction Cosine Components for T6 Coordinates | ||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> |
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> |
| <math>~2</math> | --- | --- | --- | --- | --- | <math>~\ell_q \ell_{3D} (xp^2z)</math> | <math>~\ell_q \ell_{3D} (q^2 y p^2z) </math> | <math>~- (x^2 + q^4y^2)\ell_q \ell_{3D}</math> |
| <math>~3</math> | <math>~\tan^{-1}\biggl( \frac{y^{1/q^2}}{x} \biggr)</math> | <math>~\frac{xq^2 y \ell_q}{\sin\lambda_3 \cos\lambda_3}</math> | <math>~-\frac{\sin\lambda_3 \cos\lambda_3}{x}</math> | <math>~+\frac{\sin\lambda_3 \cos\lambda_3}{q^2y}</math> | <math>~0</math> | <math>~-q^2 y \ell_q</math> | <math>~x\ell_q</math> | <math>~0</math> |
Try,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} w \, , </math> where, |
|
<math>~w</math> |
<math>~\equiv</math> |
<math>\frac{(x^2 + q^2y^2)^{1 / 2}}{z^{1/p^2}} ~~~\Rightarrow~~~\frac{1}{z^{1 / p^2} } = \frac{w}{(x^2 + q^2 y^2)^{1 / 2}} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)^{1 / 2}~z^{1/p^2}} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)^{1 / 2}~z^{1/p^2}} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{w}{1 + w^2} \biggl[- \frac{1}{p^2 z} \biggr] \, , </math> |
which means that,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{x^2}{(x^2 + q^2y^2)^2} \biggr] + \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{q^4 y^2}{(x^2 + q^2y^2)^2} \biggr] + \biggl[ \biggl( \frac{w}{1 + w^2}\biggr)^2 \frac{1}{p^4 z^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{w}{1 + w^2}\biggr)^2 \biggl[ \frac{(x^2 + q^4y^2)(p^4 z^2) + (x^2 + q^2y^2)^2}{(x^2 + q^2y^2)^2~p^4 z^2} \biggr] </math> |
|
<math>~\Rightarrow~~~ h_2</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
where,
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~[(x^2 + q^4y^2)(p^4 z^2) + (x^2 + q^2y^2)^2]^{1 / 2} \, .</math> |
Hence, the trio of associated direction cosines are,
|
<math>~\gamma_{21} = h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\}\frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] = \biggl\{ \frac{x~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
|
<math>~\gamma_{22} = h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\} \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] = \biggl\{ \frac{q^2 y~p^2 z}{ \mathcal{D}} \biggr\} \, , </math> |
|
<math>~\gamma_{23} = h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1 + w^2}{w}\biggr) \biggl\{ \frac{(x^2 + q^2y^2)~p^2 z}{ \mathcal{D}} \biggr\}\frac{w}{1 + w^2} \biggl[- \frac{1}{p^2 z} \biggr] = \biggl\{- \frac{(x^2 + q^2y^2)}{ \mathcal{D}} \biggr\} \, . </math> |
VERY close!
Let's examine the function, <math>~\mathcal{D}^2</math>.
|
<math>~\frac{1}{\ell_{3D}^2 \ell_d^2}</math> |
<math>~=</math> |
<math>~ (x^2 + q^4 y^2)(x^2 + q^4 y + p^4 z) = (x^2 + q^4 y^2)p^4 z + (x^2 + q^4 y^2)^2 \, . </math> |
Eureka (NOT!)
Try,
|
<math>~\lambda_2</math> |
<math>~\equiv</math> |
<math>~ \tan^{-1} w \, , </math> where, |
|
<math>~w</math> |
<math>~\equiv</math> |
<math>\frac{(x^2 + q^2y^2)^{1 / 2}}{p^2 z} ~~~\Rightarrow~~~\frac{1}{p^2 z } = \frac{w}{(x^2 + q^2 y^2)^{1 / 2}} \, .</math> |
The relevant partial derivatives are,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)^{1 / 2}~p^2 z} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)^{1 / 2}~p^2z} \biggr] = \frac{w}{1 + w^2} \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{1}{1 + w^2} \biggl[- \frac{(x^2 + q^2y^2)^{1 / 2}}{~p^2z^2} \biggr] = \frac{w}{1 + w^2} \biggl[- \frac{1}{z} \biggr] \, , </math> |
which means that,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{w}{1 + w^2} \biggr]^2 \biggl\{ \biggl[ \frac{x}{(x^2 + q^2y^2)} \biggr]^2 + \biggl[ \frac{q^2y}{(x^2 + q^2y^2)} \biggr]^2 + \biggl[ - \frac{1}{z} \biggr]^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{w}{1 + w^2} \biggr]^2 \biggl\{ \frac{x^2 + q^4y^2}{(x^2 + q^2y^2)^2} + \frac{1}{z^2} \biggr\} </math> |
Speculation5
Spherical Coordinates
|
<math>~r\cos\theta</math> |
<math>~=</math> |
<math>~z \, ,</math> |
|
<math>~r\sin\theta</math> |
<math>~=</math> |
<math>~(x^2 + y^2)^{1 / 2} \, ,</math> |
|
<math>~\tan\varphi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, .</math> |
Use λ1 Instead of r
Here, as above, we define,
|
<math>~\lambda_1^2</math> |
<math>~\equiv</math> |
<math>~x^2 + q^2 y^2 + p^2 z^2 </math> |
Using this expression to eliminate "x" (in favor of λ1) in each of the three spherical-coordinate definitions, we obtain,
|
<math>~r^2 \equiv x^2 + y^2 + z^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - y^2(q^2-1) - z^2(p^2-1) \, ;</math> |
|
<math>~\tan^2\theta \equiv \frac{x^2 + y^2}{z^2}</math> |
<math>~=</math> |
<math>~\frac{1}{z^2}\biggl[ \lambda_1^2 -y^2(q^2-1) -p^2z^2 \biggr] \, ;</math> |
|
<math>~\frac{1}{\tan^2\varphi} \equiv \frac{x^2}{y^2}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_1^2 - p^2z^2}{y^2} - q^2 \, . </math> |
After a bit of additional algebraic manipulation, we find that,
|
<math>\frac{z^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)}{\mathcal{D}^2} \, , </math> |
|
<math>~\frac{y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \biggl[\frac{ \mathcal{D}^2 \tan^2\varphi - p^2 \tan^2\varphi (1+\tan^2\varphi)}{(1+q^2\tan^2\varphi) \mathcal{D}^2} \biggr] \, , </math> |
|
<math>~\frac{x^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ 1 - q^2\biggl(\frac{y^2}{\lambda_1^2} \biggr) - p^2\biggl(\frac{z^2}{\lambda_1^2}\biggr) \, , </math> |
where,
|
<math>~\mathcal{D}^2</math> |
<math>~\equiv</math> |
<math>~ \biggl[ (1 + q^2\tan^2\varphi)(p^2 + \tan^2\theta) - p^2(q^2-1)\tan^2\varphi \biggr] \, . </math> |
|
As a check, let's set <math>~q^2 = p^2 = 1</math>, which should reduce to the normal spherical coordinate system.
|
Relationship To T3 Coordinates
If we set, <math>~q = 1</math>, but continue to assume that <math>~p > 1</math>, we expect to see a representation that resembles our previously discussed, T3 Coordinates. Note, for example, that the new "radial" coordinate is,
|
<math>~\lambda_1^2</math> |
<math>~\rightarrow</math> |
<math>~ (\varpi^2 + p^2z^2) \, , </math> |
and, |
<math>~\mathcal{D}^2</math> |
<math>~\rightarrow</math> |
<math>~ \biggl[ (1 + \tan^2\varphi)(p^2 + \tan^2\theta) \biggr] \, . </math> |
|
<math>~\Rightarrow ~~~ \frac{p^2z^2}{\lambda_1^2}</math> |
<math>~\rightarrow</math> |
<math>~\frac{ p^2}{(p^2 + \tan^2\theta)} = \frac{ 1}{(1 + p^{-2} \tan^2\theta)}\, ,</math> |
|
<math>~\frac{\varpi^2}{\lambda_1^2} = \frac{x^2}{\lambda_1^2} + \frac{y^2}{\lambda_1^2}</math> |
<math>~\rightarrow</math> |
<math>~1 - p^2 \biggl( \frac{z^2}{\lambda_1^2}\biggr) = \biggl[1 - \frac{ 1}{(1 + p^{-2}\tan^2\theta)} \biggr] \, .</math> |
We also see that,
|
<math>~\frac{\varpi^2}{p^2z^2}</math> |
<math>~\rightarrow</math> |
<math>~ (1 + p^{-2}\tan^2\theta)\biggl[1 - \frac{ 1}{(1 + p^{-2}\tan^2\theta)} \biggr] = p^{-2}\tan^2\theta \, . </math> |
Again Consider Full 3D Ellipsoid
Let's try to replace everywhere, <math>~[\varpi/(pz)]^2 = p^{-2}\tan^2\theta</math> with <math>~\lambda_2</math>. This gives,
|
<math>~\frac{\mathcal{D}^2}{p^2}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ (1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi \biggr] \, . </math> |
which means that,
|
<math>\frac{p^2 z^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)}{[(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi]} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ (1+\tan^2\varphi)/\tan^2\varphi}{[q^2 \lambda_2 (1 + q^2\tan^2\varphi)/(q^2\tan^2\varphi) - (q^2-1)]} = \frac{1/\sin^2\varphi}{[q^2\lambda_2 Q^2 - (q^2-1) ]} \, , </math> |
|
<math>~\frac{q^2y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } - \frac{ q^2 \tan^2\varphi (1+\tan^2\varphi)}{(1+q^2\tan^2\varphi) [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)/\tan^2\varphi}{ [q^2\lambda_2(1 + q^2\tan^2\varphi)/(q^2\tan^2\varphi) - (q^2-1) ] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ 1}{Q^2 } \biggl\{1 - \frac{ 1/\sin^2\varphi}{ [q^2\lambda_2 Q^2 - (q^2-1) ] } \biggr\} = \frac{1}{Q^2[~~]} \biggl[ [~~] - \frac{1}{\sin^2\varphi} \biggr] \, , </math> |
|
<math>~\frac{x^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~ 1 - \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } \biggl\{1 - \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
|
<math>~ - \frac{ (1+\tan^2\varphi)}{[(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi]} </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) } - \biggl\{\frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{ 1 }{ Q^2 } - \biggl\{\frac{ 1/\sin^2\varphi}{ [q^2\lambda_2 Q^2 - (q^2-1) ] } \biggr\} = \frac{1}{Q^2 [~~] } \biggl\{ Q^2[~~] - [~~] - \frac{Q^2}{\sin^2\varphi} \biggr\} \, , </math> |
|
<math>~\frac{x^2 + q^2y^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~1 - \biggl[1 + \frac{ q^2 \tan^2\varphi }{(1+q^2\tan^2\varphi) }\biggr] \biggl\{ \frac{ (1+\tan^2\varphi)}{ [(1 + q^2\tan^2\varphi)\lambda_2 - (q^2-1)\tan^2\varphi] } \biggr\} \, . </math> |
Now, notice that,
|
<math>~\frac{q^2 y^2 Q^2}{\lambda_1^2}</math> |
<math>~=</math> |
<math>~1 - \frac{1}{[~~]\sin^2\varphi} \, ,</math> |
and,
|
<math>~\frac{x^2}{\lambda_1^2} + \frac{1}{Q^2}</math> |
<math>~=</math> |
<math>~1 - \frac{1}{[~~]\sin^2\varphi} \, .</math> |
Hence,
|
<math>~\frac{x^2}{\lambda_1^2} + \frac{1}{Q^2}</math> |
<math>~=</math> |
<math>~\frac{q^2 y^2 Q^2}{\lambda_1^2}</math> |
|
<math>~\Rightarrow~~~ 0</math> |
<math>~=</math> |
<math>~Q^4 \biggl( \frac{q^2 y^2}{\lambda_1^2} \biggr) - Q^2 \biggl( \frac{x^2}{\lambda_1^2} \biggr) - 1</math> |
|
|
<math>~=</math> |
<math>~Q^4 - Q^2 \biggl( \frac{x^2}{q^2 y^2} \biggr) - \biggl( \frac{\lambda_1^2}{q^2 y^2} \biggr) \, ,</math> |
where,
|
<math>~Q^2</math> |
<math>~\equiv</math> |
<math>~\frac{1 + q^2\tan^2\varphi}{q^2\tan^2\varphi} \, .</math> |
Solving the quadratic equation, we have,
|
<math>~Q^2</math> |
<math>~=</math> |
<math>~\frac{1}{2} \biggl\{ \biggl( \frac{x^2}{q^2 y^2} \biggr) \pm \biggl[ \biggl( \frac{x^2}{q^2 y^2} \biggr)^2 + 4\biggl( \frac{\lambda_1^2}{q^2 y^2} \biggr) \biggr]^{1 / 2} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{x^2}{2q^2 y^2} \biggr) \biggl\{ 1 \pm \biggl[ 1 + 4\biggl( \frac{\lambda_1^2 q^2 y^2}{x^4} \biggr) \biggr]^{1 / 2} \biggr\} \, .</math> |
|
Tentative Summary
|
Partial Derivatives & Scale Factors
First Coordinate
|
<math>~\frac{\partial \lambda_1}{\partial x}</math> |
<math>~=</math> |
<math>~\frac{x}{\lambda_1} \, ,</math> |
|
<math>~\frac{\partial \lambda_1}{\partial y}</math> |
<math>~=</math> |
<math>~\frac{q^2 y}{\lambda_1} \, ,</math> |
|
<math>~\frac{\partial \lambda_1}{\partial z}</math> |
<math>~=</math> |
<math>~\frac{p^2 z}{\lambda_1} \, .</math> |
|
<math>~h_1^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_1}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_1}{\partial z} \biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{x}{\lambda_1} \biggr)^2 + \biggl( \frac{q^2 y}{\lambda_1} \biggr)^2 + \biggl( \frac{p^2 z}{\lambda_1} \biggr)^2 \, .</math> |
|
<math>~\Rightarrow ~~~ h_1</math> |
<math>~=</math> |
<math>~ \lambda_1 \ell_{3D} \, , </math> |
||
where,
As a result, the associated unit vector is,
|
<math>~\hat{e}_1</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_1 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr) + \hat{\jmath} h_1 \biggl( \frac{\partial \lambda_1}{\partial y} \biggr) + \hat{k} h_1 \biggl( \frac{\partial \lambda_1}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} x \ell_{3D} + \hat{\jmath} q^2 y\ell_{3D} + \hat{k} p^2 z \ell_{3D} \, . </math> |
Notice that,
|
<math>~\hat{e}_1 \cdot \hat{e}_1</math> |
<math>~=</math> |
<math>~ (x^2 + q^4 y^2 + p^4 z^2) \ell_{3D}^2 = 1 \, . </math> |
Second Coordinate (1st Try)
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{1}{pz} \biggl[ \frac{x}{(x^2 + y^2)^{1 / 2}} \biggr] \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{1}{pz} \biggl[ \frac{y}{(x^2 + y^2)^{1 / 2}} \biggr] \, ,</math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ - \frac{(x^2 + y^2)^{1 / 2}}{pz^2} \, .</math> |
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \frac{1}{pz} \biggl[ \frac{x}{(x^2 + y^2)^{1 / 2}} \biggr] \biggr\}^2 + \biggl\{ \frac{1}{pz} \biggl[ \frac{y}{(x^2 + y^2)^{1 / 2}} \biggr] \biggr\}^2 + \biggl\{ \frac{(x^2 + y^2)^{1 / 2}}{pz^2} \biggr\}^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{x^2}{(x^2 + y^2)p^2 z^2} \biggr] \biggr\} + \biggl\{ \biggl[ \frac{y^2}{(x^2 + y^2)p^2 z^2} \biggr] \biggr\} + \biggl\{ \frac{(x^2 + y^2)}{p^2 z^4} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{p^2 z^2} + \frac{(x^2 + y^2)}{p^2 z^4} = \frac{(x^2 + y^2 + z^2)}{p^2 z^4} </math> |
|
<math>~\Rightarrow~~~h_2</math> |
<math>~=</math> |
<math>~ \frac{p z^2}{r } </math> |
As a result, the associated unit vector is,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} \biggl[ \frac{xz}{r(x^2 + y^2)^{1 / 2}} \biggr] + \hat{\jmath} \biggl[ \frac{yz}{r(x^2 + y^2)^{1 / 2}} \biggr] - \hat{k} \biggl[ \frac{(x^2 + y^2)^{1 / 2}}{r} \biggr] \, . </math> |
Notice that,
|
<math>~\hat{e}_2 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{x^2 z^2}{r^2(x^2 + y^2)} \biggr] + \biggl[ \frac{y^2 z^2}{r^2(x^2 + y^2)} \biggr] + \biggl[ \frac{(x^2 + y^2)}{r^2} \biggr] = 1 \, . </math> |
Let's check to see if this "second" unit vector is orthogonal to the "first."
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ x\ell_{3D} \biggl[ \frac{xz}{r(x^2 + y^2)^{1 / 2}} \biggr] + q^2 y\ell_{3D} \biggl[ \frac{yz}{r(x^2 + y^2)^{1 / 2}} \biggr] - p^2 z \ell_{3D} \biggl[ \frac{(x^2 + y^2)^{1 / 2}}{r} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \ell_{3D} \biggl\{ \biggl[ \frac{x^2z}{r(x^2 + y^2)^{1 / 2}} \biggr] + \biggl[ \frac{q^2 y^2 z}{r(x^2 + y^2)^{1 / 2}} \biggr] - \biggl[ \frac{p^2 z(x^2 + y^2)^{1 / 2}}{r} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{z\ell_{3D}}{r (x^2 + y^2)^{1 / 2}} \biggl\{ \biggl[ x^2\biggr] + \biggl[ q^2 y^2 \biggr] - \biggl[ p^2 (x^2 + y^2) \biggr] \biggr\} </math> |
|
|
<math>~\ne</math> |
<math>~ 0 \ . </math> |
Second Coordinate (2nd Try)
Let's try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \biggl[\frac{(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2}}{pz} \biggr] \, , </math> |
|
<math>~\Rightarrow~~~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{x}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } = \frac{x}{p^2 z^2 \lambda_2} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{q^2 y}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } = \frac{q^2y}{p^2 z^2 \lambda_2} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ \frac{\mathfrak{f}\cdot p^2z}{pz(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2} } - \frac{(x^2 + q^2y^2 + \mathfrak{f}\cdot p^2 z^2)^{1 / 2}}{pz^2} = \frac{1}{p^2z^2 \lambda_2 } \biggl( \mathfrak{f}\cdot p^2z \biggr) - \frac{\lambda_2 }{z} = \frac{1}{p^2z^2 \lambda_2 } \biggl( \mathfrak{f}\cdot p^2z - p^2z \lambda_2^2 \biggr) \, . </math> |
Hence,
|
<math>~h_2^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{x}{p^2 z^2 \lambda_2} \biggr]^2 + \biggl[ \frac{q^2y}{p^2 z^2 \lambda_2} \biggr]^2 + \biggl[ \frac{ \mathfrak{f} }{z \lambda_2 } - \frac{\lambda_2 }{z}\biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{x^2 + q^4 y^2}{p^4 z^4 \lambda_2^2} \biggr] + \biggl[ \frac{1}{z\lambda_2}\biggl( \mathfrak{f} - \lambda_2^2 \biggr) \biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{p^4 z^4 \lambda_2^2} \biggl[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 \biggr] </math> |
|
<math>~\Rightarrow ~~~ h_2</math> |
<math>~=</math> |
<math>~ \frac{p^2 z^2 \lambda_2}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \, . </math> |
So, the associated unit vector is,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \hat{\imath} \biggl\{ \frac{x}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + \hat{\jmath} \biggl\{ \frac{q^2 y}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + \hat{k} \biggl\{ \frac{p^2z(\mathfrak{f}-\lambda_2^2)}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} \, . </math> |
Checking orthogonality …
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ x\ell_{3D} \biggl\{ \frac{x}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + q^2 y\ell_{3D} \biggl\{ \frac{q^2 y}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} + p^2 z \ell_{3D} \biggl\{ \frac{p^2z(\mathfrak{f}-\lambda_2^2)}{[ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
If <math>~\mathfrak{f} = 0</math>, we have …
|
<math>~p^2 z (\mathfrak{f} - \lambda_2^2) </math> |
<math>~~~\rightarrow ~~~ </math> |
<math>~ \biggl[- p^2 z \lambda_2^2\biggr]_{\mathfrak{f} = 0} = - p^2 z\biggl[\frac{(x^2 + q^2y^2 + \cancelto{0}{\mathfrak{f} \cdot }p^2 z^2 )^{1 / 2}}{pz} \biggr]^2 = - \frac{(x^2 + q^2y^2 )}{z} \, ,</math> |
which, in turn, means …
|
<math>~[ x^2 + q^4 y^2 + p^4 z^2 (\cancelto{0}{\mathfrak{f}} - \lambda_2^2)^2 ]^{1 / 2}</math> |
<math>~=</math> |
<math>~ [ x^2 + q^4 y^2 + p^4 z^2 \lambda_2^4 ]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ x^2 + q^4 y^2 + p^4 z^2 \biggl[\frac{(x^2 + q^2y^2 + \cancelto{0}{\mathfrak{f}\cdot} p^2 z^2)^{1 / 2}}{pz} \biggr]^4 \biggr\}^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ x^2 + q^4 y^2 + \biggl[\frac{(x^2 + q^2y^2 )^{2}}{z^2} \biggr] \biggr\}^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ (x^2 + q^4 y^2)^{1 / 2} \biggl[ 1 + \frac{(x^2 + q^2y^2 )}{z^2} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{(x^2 + q^4 y^2)^{1 / 2}}{z} \biggl[ z^2 + (x^2 + q^2y^2 ) \biggr]^{1 / 2} \, , </math> |
and,
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{ [ x^2 + q^4 y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)^2 ]^{1 / 2} } \biggl\{ x^2 + q^4y^2 + p^4 z^2 (\mathfrak{f} - \lambda_2^2)\biggr\} \, . </math> |
Speculation6
Determine λ2
This is very similar to the above, Speculation2. Try,
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, , </math> |
in which case,
|
<math>~\frac{\partial \lambda_2}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{\lambda_2}{x} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{x}{z^{2/p^2}} \biggl(\frac{1}{q^2}\biggr) y^{1/q^2 - 1} = \frac{\lambda_2}{q^2 y} \, , </math> |
|
<math>~\frac{\partial \lambda_2}{\partial z}</math> |
<math>~=</math> |
<math>~ -\frac{2\lambda_2}{p^2 z} \, . </math> |
The associated scale factor is, then,
|
<math>~h_2</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_2}{\partial x} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial y} \biggr)^2 + \biggl( \frac{\partial \lambda_2}{\partial z} \biggr)^2 \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{ \lambda_2}{x} \biggr)^2 + \biggl( \frac{\lambda_2}{q^2y} \biggr)^2 + \biggl( - \frac{2\lambda_2}{p^2z} \biggr)^2 \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\lambda_2}\biggl[ \frac{ 1}{x^2} + \frac{1}{q^4y^2} + \frac{4}{p^4z^2} \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\lambda_2}\biggl[ \frac{ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2}{x^2 q^4 y^2 p^4 z^2} \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\lambda_2}\biggl[ \frac{x q^2 y p^2 z}{ \mathcal{D}} \biggr] \, . </math> |
where,
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
The associated unit vector is, then,
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat{\imath} h_2 \biggl( \frac{\partial \lambda_2}{\partial x} \biggr) + \hat{\jmath} h_2 \biggl( \frac{\partial \lambda_2}{\partial y} \biggr) + \hat{k} h_2 \biggl( \frac{\partial \lambda_2}{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl\{ \hat{\imath} \biggl( \frac{1}{x} \biggr) + \hat{\jmath} \biggl( \frac{1}{q^2 y} \biggr) + \hat{k} \biggl( -\frac{2}{p^2 z} \biggr) \biggr\} \ . </math> |
Recalling that the unit vector associated with the "first" coordinate is,
|
<math>~\hat{e}_1 </math> |
<math>~\equiv</math> |
<math>~ \hat\imath (x \ell_{3D}) + \hat\jmath (q^2y \ell_{3D}) + \hat{k} (p^2 z \ell_{3D}) \, , </math> |
where,
|
<math>~\ell_{3D}</math> |
<math>~=</math> |
<math>~(x^2 + q^4y^2 + p^4 z^2 )^{- 1 / 2} \, ,</math> |
let's check to see whether the "second" unit vector is orthogonal to the "first."
|
<math>~\hat{e}_1 \cdot \hat{e}_2</math> |
<math>~=</math> |
<math>~ \frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl[ 1 + 1 - 2 \biggr] = 0 \, . </math> |
Hooray!
Direction Cosines for Third Unit Vector
Now, what is the unit vector, <math>~\hat{e}_3</math>, that is simultaneously orthogonal to both these "first" and the "second" unit vectors?
|
<math>~\hat{e}_3 \equiv \hat{e}_1 \times \hat{e}_2</math> |
<math>~=</math> |
<math>~ \hat\imath \biggl[ ( e_{1y} )( e_{2z}) - ( e_{2y} )( e_{1z}) ) \biggl] + \hat\jmath \biggl[ ( e_{1z} )( e_{2x}) - ( e_{2z} )( e_{1x}) ) \biggl] + \hat{k} \biggl[ ( e_{1x} )( e_{2y}) - ( e_{2x} )( e_{1y}) ) \biggl] </math> |
|
|
<math>~=</math> |
<math>~\frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl\{ \hat\imath \biggl[ \biggl( -\frac{2 q^2y}{p^2 z} \biggr) - \biggl( \frac{p^2z}{q^2y} \biggr) \biggl] + \hat\jmath \biggl[ \biggl( \frac{p^2z}{x} \biggr) - \biggl(-\frac{2x}{p^2z} \biggr) \biggl] + \hat{k} \biggl[ \biggl( \frac{x}{q^2y} \biggr) - \biggl( \frac{q^2y}{x} \biggr) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{(x q^2 y p^2 z) \ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ \frac{2 q^4y^2 + p^4z^2}{q^2 y p^2 z} \biggl] + \hat\jmath \biggl[ \frac{p^4z^2 + 2x^2}{xp^2 z} \biggl] + \hat{k} \biggl[ \frac{x^2 - q^4y^2}{x q^2y} \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + \hat\jmath \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + \hat{k} \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} \, . </math> |
Is this a valid unit vector? First, note that …
|
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2}</math> |
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) (x^2 + q^4y^2 + p^4 z^2 ) </math> |
|
|
<math>~=</math> |
<math>~ (x^2 q^4 y^2 p^4 z^2 + x^4 p^4 z^2 + 4x^4q^4y^2) + (q^8 y^4 p^4 z^2 + x^2 q^4y^2 p^4 z^2 + 4x^2q^8y^4) +(q^4 y^2 p^8 z^4 + x^2 p^8 z^4 + 4x^2q^4y^2 p^4 z^2) </math> |
|
|
<math>~=</math> |
<math>~ 6x^2 q^4 y^2 p^4 z^2 + x^4(p^4 z^2 + 4 q^4y^2) + q^8 y^4(p^4 z^2 + 4x^2) +p^8z^4(x^2 + q^4 y^2 )\, . </math> |
Then we have,
|
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2}\hat{e}_3 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~ \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2 </math> |
|
|
<math>~=</math> |
<math>~ x^2(4 q^8y^4 + 4q^4y^2p^4z^2 + p^8z^4 ) + q^4 y^2(p^8z^4 + 4x^2p^4z^2 + 4x^4 ) + p^4z^2( x^4 - 2x^2q^4 y^2 + q^8y^4 ) </math> |
|
|
<math>~=</math> |
<math>~ 4 x^2 q^8y^4 + 4x^2 q^4y^2p^4z^2 + x^2 p^8z^4 + q^4 y^2p^8z^4 + 4x^2q^4 y^2p^4z^2 + 4x^4q^4 y^2 + x^4p^4z^2 - 2x^2q^4 y^2p^4z^2 + q^8y^4p^4z^2 </math> |
|
|
<math>~=</math> |
<math>~ 6x^2 q^4y^2p^4z^2 + p^8z^4 (x^2 +q^4 y^2) + x^4(4q^4 y^2 + p^4z^2) + q^8 y^4(4 x^2 + p^4z^2 ) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2} \, , </math> |
which means that, <math>~\hat{e}_3\cdot \hat{e}_3 = 1</math>. Hooray! Again (11/11/2020)!
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
Let's double-check whether this "third" unit vector is orthogonal to both the "first" and the "second" unit vectors.
|
<math>~\hat{e}_1 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}^2}{\mathcal{D}} \biggl\{ -x \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + q^2 y \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + p^2 z \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{\ell_{3D}^2}{\mathcal{D}} \biggl\{ - (2 x^2q^4y^2 + x^2p^4z^2 ) + (q^4 y^2 p^4z^2 + 2x^2 q^4 y^2) + ( x^2p^4z^2 - q^4y^2 p^4z^2 ) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 0 \, , </math> |
and,
|
<math>~\hat{e}_2 \cdot \hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \cdot \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl\{ - \biggl[ (2 q^4y^2 + p^4z^2 ) \biggl] + \biggl[ (p^4z^2 + 2x^2 ) \biggl] - \biggl[ 2( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
Q. E. D.
Search for Third Coordinate Expression
Let's try …
|
<math>~\lambda_3</math> |
<math>~=</math> |
<math>~\mathcal{D}^n \ell_{3D}^m </math> |
|
|
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{n / 2} (x^2 + q^4y^2 + p^4 z^2 )^{- m / 2} </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ \ell_{3D}^m \biggl[ \frac{n}{2} \biggl(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr)^{n / 2 - 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)\biggr] </math> |
|
|
|
<math>~ + \mathcal{D}^n \biggl[ - \frac{m}{2} (x^2 + q^4y^2 + p^4 z^2 )^{- m / 2 - 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(x^2 + q^4y^2 + p^4 z^2 )\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \mathcal{D}^n \ell_{3D}^m \biggl[ \frac{n}{2} \biggl(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr)^{- 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)\biggr] </math> |
|
|
|
<math>~ + \mathcal{D}^n \ell_{3D}^m \biggl[ - \frac{m}{2} (x^2 + q^4y^2 + p^4 z^2 )^{- 1} \biggr] \frac{\partial}{\partial x_i} \biggl[(x^2 + q^4y^2 + p^4 z^2 )\biggr] \, . </math> |
Hence,
|
<math>~\frac{1}{\mathcal{D}^n \ell_{3D}^m} \cdot \frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~ \frac{n}{2\mathcal{D}^2}\frac{\partial}{\partial x} \biggl[q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 \biggr] - \frac{m \ell_{3D}^2}{2} \frac{\partial}{\partial x} \biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~x \biggl\{ \frac{n}{\mathcal{D}^2}\biggl[p^4 z^2 + 4q^4y^2 \biggr] - m \ell_{3D}^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~x \biggl\{ \frac{n (p^4 z^2 + 4q^4y^2)}{ ( q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2 ) } - \frac{m}{ ( x^2 + q^4y^2 + p^4 z^2 ) } \biggr\} </math> |
This is overly cluttered! Let's try, instead …
|
Now, let's assume that,
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{A}{B} \biggr)^{1 / 2} \, ,</math> |
|
<math>~\Rightarrow~~~ \frac{ \partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ \frac{1}{2 (AB)^{1 / 2}} \cdot \frac{\partial A}{\partial x_i} - \frac{A^{1 / 2}}{2 B^{3 / 2}} \cdot \frac{\partial B}{\partial x_i} </math> |
|
|
<math>~=</math> |
<math>~\frac{\lambda_3}{2AB} \biggl[ B \cdot \frac{\partial A}{\partial x_i} - A \cdot \frac{\partial B}{\partial x_i} \biggr] \, . </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~=</math> |
<math>~ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) \cdot \frac{\partial A}{\partial x_i} - (x^2 + q^4y^2 + p^4 z^2 ) \cdot \frac{\partial B}{\partial x_i} \, . </math> |
|
Looking ahead …
Then, for example,
|
As a result, we have,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x}</math> |
<math>~=</math> |
<math>~2x \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) ( 4q^4y^2 + p^4 z^2 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2x \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (4x^2q^4y^2 + x^2 p^4 z^2 + 4q^8y^4 + q^4y^2 p^4z^2 + 4q^4y^2 p^4 z^2 + p^8z^4) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2x \biggl[ - (4q^8y^4 + 4q^4y^2 p^4 z^2 + p^8z^4) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2x (2q^4y^2 + p^4z^2)^2 </math> |
|
|
<math>~=</math> |
<math>~-8x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln\lambda_3}{\partial \ln{x}}</math> |
<math>~=</math> |
<math>~-\biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 \, ; </math> |
and,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial y}</math> |
<math>~=</math> |
<math>~ 2q^4y\biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) (p^4 z^2 + 4x^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2q^4y\biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - ( x^2p^4z^2 + 4x^4 + q^4y^2p^4z^2 + 4x^2q^4y^2 + p^8z^4 + 4x^2p^4z^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -2q^4y( 4x^4 + p^8z^4 + 4x^2p^4z^2) </math> |
|
|
<math>~=</math> |
<math>~ -2q^4y( 2x^2 + p^4z^2 )^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln\lambda_3}{\partial \ln{y} }</math> |
<math>~=</math> |
<math>~ - \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^2 \, ; </math> |
and,
|
<math>~\Rightarrow ~~~\biggl[ \frac{2AB}{\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial z}</math> |
<math>~=</math> |
<math>~2p^4 z \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2 + q^4y^2 + p^4 z^2 ) (q^4 y^2 + x^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2p^4 z \biggl[ (q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) - (x^2q^4y^2 + x^4 + q^8y^4 + x^2q^4y^2 + q^4y^2p^4z^2 + x^2p^4z^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~2p^4 z \biggl[ ( 2x^2q^4y^2) - ( x^4 + q^8y^4 ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2p^4 z \biggl[ x^4 + q^8y^4 - 2x^2q^4y^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~-2p^4 z (x^2 - q^4y^2 )^2 </math> |
|
<math>~\Rightarrow ~~~\biggl[ AB \biggr] \frac{\partial \ln \lambda_3}{\partial \ln{z}}</math> |
<math>~=</math> |
<math>~-4 \biggl[ \biggl( \frac{p^4 z^2}{4} \biggr) (x^2 - q^4y^2 )^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~-\biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^2 \, . </math> |
Wow! Really close! (13 November 2020)
Just for fun, let's see what we get for <math>~h_3</math>. It is given by the expression,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_3}{\partial x} \biggr)^2 +\biggl( \frac{\partial \lambda_3}{\partial y} \biggr)^2 +\biggl( \frac{\partial \lambda_3}{\partial z} \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \frac{\lambda_3}{ABx} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 \biggr\}^2 +\biggl\{ \frac{\lambda_3}{ABy} \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^2 \biggr\}^2 +\biggl\{ \frac{\lambda_3}{ABz} \biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^2 \biggr\}^2 </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{AB}{\lambda_3}\biggr]^2 h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{1}{x^2} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^4 \biggr\} +\biggl\{ \frac{1}{y^2} \biggl[2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr) \biggr]^4 \biggr\} +\biggl\{ \frac{1}{z^2} \biggl[ 2\biggl( \frac{p^2 z}{2} \biggr) (x^2 - q^4y^2 ) \biggr]^4 \biggr\} </math> |
Fiddle Around
Let …
|
<math>~\mathcal{L}_x</math> |
<math>~\equiv</math> |
<math>~ - \biggl[ B \cdot \frac{\partial A}{\partial x} - A \cdot \frac{\partial B}{\partial x} \biggr] </math> |
<math>~=</math> |
<math>~8x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
<math>~=</math> |
<math>~\frac{2}{x} \biggl[ 2x \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8x~\mathfrak{F}_x(y,z) </math> |
|
<math>~\mathcal{L}_y</math> |
<math>~\equiv</math> |
<math>~ - \biggl[ B \cdot \frac{\partial A}{\partial y} - A \cdot \frac{\partial B}{\partial y} \biggr] </math> |
<math>~=</math> |
<math>~ 8q^4y\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2 </math> |
<math>~=</math> |
<math>~ \frac{2}{y} \biggl[ 2q^2y\biggl( x^2 + \frac{p^4z^2}{2} \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8y~\mathfrak{F}_y(x,z) </math> |
|
<math>~\mathcal{L}_z</math> |
<math>~\equiv</math> |
<math>~ -\biggl[ B \cdot \frac{\partial A}{\partial z} - A \cdot \frac{\partial B}{\partial z} \biggr] </math> |
<math>~=</math> |
<math>~ 2p^4 z \biggl(x^2 - q^4y^2 \biggr)^2 </math> |
<math>~=</math> |
<math>~ \frac{2}{z} \biggl[p^2 z \biggl(x^2 - q^4y^2 \biggr)\biggr]^2 </math> |
<math>~=</math> |
<math>~8z~\mathfrak{F}_z(x,y) </math> |
With this shorthand in place, we can write,
|
<math>~\hat{e}_3</math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl] + \hat\jmath \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl] + \hat{k} \biggl[ p^2z( x^2 - q^4y^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl\{ -\hat\imath \biggl[ \frac{x \mathcal{L}_x}{2} \biggl]^{1 / 2} + \hat\jmath \biggl[ \frac{y \mathcal{L}_y}{2} \biggl]^{1 / 2} + \hat{k} \biggl[ \frac{z \mathcal{L}_z}{2} \biggl]^{1 / 2} \biggr\} \, . </math> |
We therefore also recognize that,
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)</math> |
<math>~=</math> |
<math>~ -\frac{1}{(AB)^{1 / 2}} \biggl[ \frac{x \mathcal{L}_x}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ -\frac{1}{(AB)^{1 / 2}} \biggl[ 4x^2 ~\mathfrak{F}_x \biggl]^{1 / 2} \, , </math> |
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)</math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ \frac{y \mathcal{L}_y}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ 4y^2~\mathfrak{F}_y \biggl]^{1 / 2} \, , </math> |
|
<math>~h_3 \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)</math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ \frac{z \mathcal{L}_z}{2} \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ \frac{1}{(AB)^{1 / 2}} \biggl[ 4z^2~\mathfrak{F}_z \biggl]^{1 / 2} \, . </math> |
Now, if — and it is a BIG "if" — <math>~h_3 = h_0(AB)^{-1 / 2}</math>, then we have,
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)</math> |
<math>~=</math> |
<math>~ -\biggl[ 4x^2 ~\mathfrak{F}_x \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ -2x \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} \, , </math> |
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)</math> |
<math>~=</math> |
<math>~ \biggl[ 4y^2~\mathfrak{F}_y \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ 2y \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} \, , </math> |
|
<math>~h_0 \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)</math> |
<math>~=</math> |
<math>~ \biggl[ 4z^2~\mathfrak{F}_z \biggl]^{1 / 2} </math> |
<math>~=</math> |
<math>~ 2z\biggl[ \mathfrak{F}_z \biggl]^{1 / 2} \, , </math> |
|
<math>~\Rightarrow~~~ h_0 \lambda_3</math> |
<math>~=</math> |
<math>~ -x^2 \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} + y^2 \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} + z^2 \biggl[ \mathfrak{F}_z \biggl]^{1 / 2} \, . </math> |
But if this is the correct expression for <math>~\lambda_3</math> and its three partial derivatives, then it must be true that,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\partial \lambda_3}{\partial x}\biggr)^2 + \biggl(\frac{\partial \lambda_3}{\partial y}\biggr)^2 + \biggl(\frac{\partial \lambda_3}{\partial z}\biggr)^2 </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{h_3}{h_0}\biggr)^{-2}</math> |
<math>~=</math> |
<math>~ 4x^2 \biggl[ \mathfrak{F}_x \biggl] + 4y^2 \biggl[ \mathfrak{F}_y \biggl] + 4z^2\biggl[ \mathfrak{F}_z \biggl] </math> |
|
|
<math>~=</math> |
<math>~ 4x^2 \biggl[ \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 \biggl] + 4y^2 \biggl[ q^4\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2\biggl] + 4z^2\biggl[ \frac{p^4}{4}\biggl(x^2 - q^4y^2 \biggr)^2 \biggl] </math> |
|
|
<math>~=</math> |
<math>~ x^2 (2q^4y^2 + p^4z^2 )^2 + q^4 y^2( 2x^2 + p^4z^2 )^2 + p^4 z^2 (x^2 - q^4y^2 )^2 </math> |
Well … the right-hand side of this expression is identical to the right-hand side of the above expression, where we showed that it equals <math>~(\ell_{3D}/\mathcal{D})^{-2}</math>. That is to say, we are now showing that,
|
<math>~\biggl( \frac{h_3}{h_0}\biggr)^{-2}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr)^{-2} = [AB]</math> |
|
<math>~\Rightarrow ~~~ \frac{h_3}{h_0}</math> |
<math>~=</math> |
<math>~(AB)^{-1 / 2} \, .</math> |
And this is precisely what, just a few lines above, we hypothesized the functional expression for <math>~h_3</math> ought to be. EUREKA!
Summary
In summary, then …
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ -x^2 \biggl[ \mathfrak{F}_x \biggl]^{1 / 2} + y^2 \biggl[ \mathfrak{F}_y \biggl]^{1 / 2} + z^2 \biggl[ \mathfrak{F}_z \biggl]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ -x^2 \biggl[\biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr)^2 \biggl]^{1 / 2} + y^2 \biggl[ q^4\biggl( x^2 + \frac{p^4z^2}{2} \biggr)^2\biggl]^{1 / 2} + z^2 \biggl[ \frac{p^4}{4} \biggl(x^2 - q^4y^2 \biggr)^2 \biggl]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ -x^2 \biggl(q^4y^2 + \frac{p^4z^2}{2} \biggr) + q^2y^2 \biggl( x^2 + \frac{p^4z^2}{2} \biggr) + \frac{p^2 z^2}{2} \biggl(x^2 - q^4y^2 \biggr) \, , </math> |
and,
|
<math>~h_3</math> |
<math>~=</math> |
<math>~(AB)^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ (x^2 + q^4y^2 + p^4 z^2 )(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2) \biggr]^{-1 / 2} \, .</math> |
No! Once again this does not work. The direction cosines — and, hence, the components of the <math>~\hat{e}_3</math> unit vector — are not correct!
Speculation7
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
On my white-board I have shown that, if
<math>~\lambda_3 \equiv \ell_{3D} \mathcal{D} \, ,</math>
then everything will work out as long as,
|
<math>~\mathcal{L}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\mathcal{D}}{\ell_{3D}} \biggr)^2 \frac{1}{\ell_{3D}^4} \, , </math> |
where,
|
<math>~\mathcal{L}</math> |
<math>~\equiv</math> |
<math>~ x^2 (2q^4 y^2 + p^4z^2 )^4 + q^8 y^2 (2x^2 + p^4 z^2)^4 + p^8z^2( x^2 - q^4y^2)^4 </math> |
|
|
<math>~=</math> |
<math>~ x^2 (4q^8 y^4 + 4q^4y^2p^4z^2 + p^8z^4 )^2 + q^8 y^2 (4x^4 + 4x^2p^4z^2 + p^8 z^4)^2 + p^8z^2( x^4 - 2x^2q^4y^2 + q^8y^4)^2 </math> |
|
|
<math>~=</math> |
<math>~ x^2 [16q^{16}y^8 + 16q^{12}y^6p^4z^2 + 4q^8y^4p^8z^4 + 16q^{12}y^6p^4z^2 + 16q^8y^4p^8z^4 + 4q^4y^2p^{12}z^6 + 4q^8y^4p^8z^4 + 4q^4y^2 p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + q^8 y^2 [16x^8 + 16x^6p^4z^2 + 4x^4p^8z^4 + 16x^6p^4z^2 + 16x^4p^8z^4 + 4x^2p^{12}z^6 + 4x^4p^8z^4 + 4x^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + p^8z^2 [x^8 - 2x^6q^4y^2 + x^4q^8y^4 - 2x^6q^4y^2 + 4x^4q^8y^4 - 2x^2q^{12}y^6 + x^4q^8y^4 - 2x^2q^{12}y^6 + q^{16}y^8] </math> |
|
|
<math>~=</math> |
<math>~ x^2 [16q^{16}y^8 + 32q^{12}y^6p^4z^2 + 24q^8y^4p^8z^4 + 8q^4y^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + q^8 y^2 [16x^8 + 32x^6p^4z^2 + 24x^4p^8z^4 + 8x^2p^{12}z^6 + p^{16}z^8] </math> |
|
|
|
<math>~ + p^8z^2 [x^8 - 4x^6q^4y^2 + 6x^4q^8y^4 - 4x^2q^{12}y^6 + q^{16}y^8] </math> |
Let's check this out.
|
<math>~\mathrm{RHS}~\equiv \biggl(\frac{\mathcal{D}}{\ell_{3D}} \biggr)^2 \frac{1}{\ell_{3D}^4}</math> |
<math>~=</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)(x^2 + q^4y^2 + p^4 z^2 )^3</math> |
|
|
<math>~=</math> |
<math>~(x^2 + q^4y^2 + p^4 z^2 )(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)[x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
|
|
<math>~=</math> |
<math>~ [(6x^2q^4 y^2 p^4 z^2 + x^4 p^4 z^2 + 4x^4q^4y^2) + (q^8 y^4 p^4 z^2 + 4x^2q^8 y^4) + (q^4 y^2 p^8 z^4 + x^2 p^8 z^4 )] </math> |
|
|
|
<math>~\times [x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
|
|
<math>~=</math> |
<math>~ [6x^2q^4 y^2 p^4 z^2 + x^4(p^4 z^2 + 4q^4y^2) + q^8 y^4(p^4 z^2 + 4x^2) + p^8 z^4 (q^4 y^2 + x^2 )] </math> |
|
|
|
<math>~\times [x^4 + 2x^2q^4y^2 + 2x^2p^4z^2 +q^8y^4 + 2q^4y^2p^4z^2 + p^8z^4]</math> |
Best Thus Far
Part A
| Direction Cosine Components for T6 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~2</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~3</math> | --- | --- | --- | --- | --- | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
|
Try …
|
<math>~\lambda_3</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{B}{A}\biggr)^{m/2} = (D \ell_{3D})^m </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{AB}{m\lambda_3} \biggr] \frac{\partial \lambda_3}{\partial x_i}</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{2}\biggl\{ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr\} </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln x_i}</math> |
<math>~\equiv</math> |
<math>~ \frac{x_i}{2}\biggl\{ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr\} \, . </math> |
In this case we find,
|
<math>~\frac{x}{2}\biggl\{~~\biggr\}_x</math> |
<math>~=</math> |
<math>~ x^2(2q^4 y^2 + p^4z^2)^2 \, , </math> |
|
<math>~\frac{y}{2}\biggl\{~~\biggr\}_y</math> |
<math>~=</math> |
<math>~ q^4y^2(2x^2 + p^4 z^2)^2 \, , </math> |
|
<math>~\frac{z}{2}\biggl\{~~\biggr\}_z</math> |
<math>~=</math> |
<math>~ p^4 z^2(x^2 - q^4y^2)^2 \, . </math> |
The scale factor is, then,
|
<math>~h_3^{-2}</math> |
<math>~=</math> |
<math>~ \sum_{i=1}^3 \biggl( \frac{\partial\lambda_3}{\partial x_i}\biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \sum_{i=1}^3 \biggl\{ \biggl[ \frac{m\lambda_3}{2AB} \biggr] \biggl[ A \cdot \frac{\partial B}{\partial x_i} - B \cdot \frac{\partial A}{\partial x_i} \biggr] \biggr\}^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{m\lambda_3}{AB} \biggr]^2 \biggl\{ \biggl[ x(2q^4 y^2 + p^4z^2)^2 \biggr]^2 + \biggl[ q^4y(2x^2 + p^4 z^2)^2 \biggr]^2 + \biggl[ p^4 z(x^2 - q^4y^2)^2 \biggr]^2 \biggr\} </math> |
|
<math>~\Rightarrow~~~h_3</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{AB}{m\lambda_3} \biggr] \biggl\{ \biggl[ x(2q^4 y^2 + p^4z^2)^2 \biggr]^2 + \biggl[ q^4y(2x^2 + p^4 z^2)^2 \biggr]^2 + \biggl[ p^4 z(x^2 - q^4y^2)^2 \biggr]^2 \biggr\}^{-1 / 2} \, . </math> |
Part B (25 February 2021)
Now, from above, we know that,
|
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} = AB</math> |
<math>~=</math> |
<math>~ \biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2 \, . </math> |
|
Example: |
|||
| <math>~\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]^2</math> | <math>~\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]^2</math> | <math>~\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]^2</math> | <math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math> |
| 2.14037 | 1.39187 | 0.04623 | 3.57847 |
As an aside, note that,
|
<math>~AB</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln x} + \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln y} + \biggl[ \frac{AB}{m} \biggr] \frac{\partial \ln \lambda_3}{\partial \ln z} </math> |
|
<math>~\Rightarrow ~~~ m</math> |
<math>~=</math> |
<math>~ \frac{\partial \ln \lambda_3}{\partial \ln x} + \frac{\partial \ln \lambda_3}{\partial \ln y} + \frac{\partial \ln \lambda_3}{\partial \ln z} \, . </math> |
We realize that this ratio of lengths may also be written in the form,
|
<math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} </math> |
<math>~=</math> |
<math>~ 6x^2 q^4y^2 p^4 z^2 + x^4(4q^4y^2 + p^4z^2) + q^8y^4(4x^2 + p^4z^2) + p^8z^4(x^2 + q^4y^2) \, . </math> |
|
Same Example, but Different Expression: |
||||
| <math>~6x^2 q^4y^2 p^4 z^2</math> | <math>~x^4(4q^4y^2 + p^4z^2)</math> | <math>~q^8y^4(4x^2 + p^4z^2)</math> | <math>~p^8z^4(x^2 + q^4y^2)</math> | <math>~\biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2}</math> |
| 0.67620 | 0.94359 | 1.87054 | 0.08813 | 3.57847 |
Let's try …
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~-x(2 q^4y^2 + p^4z^2 ) \, ,</math> |
|
<math>~\frac{\partial \lambda_5}{\partial y}</math> |
<math>~=</math> |
<math>~q^2 y(p^4z^2 + 2x^2 ) \, ,</math> |
|
<math>~\frac{\partial \lambda_5}{\partial z}</math> |
<math>~=</math> |
<math>~p^2z( x^2 - q^4y^2 ) \, .</math> |
This means that the relevant scale factor is,
|
<math>~h_5^{-2}</math> |
<math>~=</math> |
<math>~ \biggl[ -x(2 q^4y^2 + p^4z^2 ) \biggr]^2 + \biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggr]^2 + \biggl[ p^2z( x^2 - q^4y^2 ) \biggr]^2 = \biggl( \frac{\mathcal{D}}{\ell_{3D}} \biggr)^{2} </math> |
|
<math>~\Rightarrow~~~h_5</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, , </math> |
and the three associated direction cosines are,
|
<math>~\gamma_{51} = h_5 \biggl( \frac{\partial \lambda_5}{\partial x} \biggr)</math> |
<math>~=</math> |
<math>~-x(2 q^4y^2 + p^4z^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> |
|
<math>~\gamma_{52} = h_5 \biggl( \frac{\partial \lambda_5}{\partial y} \biggr)</math> |
<math>~=</math> |
<math>~q^2 y(p^4z^2 + 2x^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, ,</math> |
|
<math>~\gamma_{53} = h_5 \biggl( \frac{\partial \lambda_5}{\partial z} \biggr)</math> |
<math>~=</math> |
<math>~p^2z( x^2 - q^4y^2 )\biggl( \frac{\ell_{3D}}{\mathcal{D}} \biggr) \, .</math> |
These direction cosines exactly match what is required in order to ensure that the coordinate, <math>~\lambda_5</math>, is everywhere orthogonal to both <math>~\lambda_1</math> and <math>~\lambda_4</math>. GREAT! The resulting summary table is, therefore:
| Direction Cosine Components for T10 Coordinates | ||||||||||||||
| <math>~n</math> | <math>~\lambda_n</math> | <math>~h_n</math> | <math>~\frac{\partial \lambda_n}{\partial x}</math> | <math>~\frac{\partial \lambda_n}{\partial y}</math> | <math>~\frac{\partial \lambda_n}{\partial z}</math> | <math>~\gamma_{n1}</math> | <math>~\gamma_{n2}</math> | <math>~\gamma_{n3}</math> | ||||||
| <math>~1</math> | <math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} </math> | <math>~\lambda_1 \ell_{3D}</math> | <math>~\frac{x}{\lambda_1}</math> | <math>~\frac{q^2 y}{\lambda_1}</math> | <math>~\frac{p^2 z}{\lambda_1}</math> | <math>~(x) \ell_{3D}</math> | <math>~(q^2 y)\ell_{3D}</math> | <math>~(p^2z) \ell_{3D}</math> | ||||||
| <math>~4</math> | <math>~\frac{x y^{1/q^2}}{ z^{2/p^2}}</math> | <math>~\frac{1}{\lambda_2}\biggl[\frac{x q^2 y p^2 z}{ \mathcal{D}}\biggr] </math> | <math>~\frac{\lambda_2}{x}</math> | <math>~\frac{\lambda_2}{q^2 y}</math> | <math>~-\frac{2\lambda_2}{p^2 z}</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{x}\biggr)</math> | <math>~ \frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(\frac{1}{q^2y}\biggr)</math> | <math>~\frac{x q^2 y p^2 z}{\mathcal{D}} \biggl(-\frac{2}{p^2z}\biggr)</math> | ||||||
| <math>~5</math> | --- | <math>~\frac{\ell_{3D}}{\mathcal{D}}</math> | <math>~-x(2 q^4y^2 + p^4z^2)</math> | <math>~q^2 y(p^4z^2 + 2x^2 )</math> | <math>~p^2z( x^2 - q^4y^2 )</math> | <math>~-\frac{\ell_{3D}}{\mathcal{D}}\biggl[ x(2 q^4y^2 + p^4z^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ q^2 y(p^4z^2 + 2x^2 ) \biggl]</math> | <math>~\frac{\ell_{3D}}{\mathcal{D}}\biggl[ p^2z( x^2 - q^4y^2 ) \biggl]</math> | ||||||
|
||||||||||||||
Try …
|
<math>~\lambda_5</math> |
<math>~=</math> |
<math>~ x^{-2q^4} \cdot y^{2q^2} + y^{q^2p^4} \cdot z^{-q^4p^2} + x^{-p^4} \cdot z^{p^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ y^{2q^2} }{ x^{2q^4} } + \frac{ y^{q^2p^4} }{ z^{q^4p^2} } + \frac{ z^{p^4} }{ x^{p^2} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ [x^{p^2}] y^{2q^2} [z^{q^4p^2}] + [x^{2q^4 + p^2}]y^{q^2p^4} + [x^{2q^4}]z^{p^4+q^4p^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^{2q^4 + p^2} z^{q^4p^2} }\biggl\{ \mathfrak{F_5} \biggr\} \, . </math> |
This gives,
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~ -\frac{2q^4}{x}\biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) - \frac{p^4}{x}\biggl( \frac{ z^{p^2} }{ x^{p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{1}{x^{2q^4 + p^2 + 1}}\biggl[ 2q^4y^{2q^2} x^{p^2} + p^4 x^{2q^4}z^{p^2} \biggr] \, . </math> |
Or, given that,
|
<math>~x^{2q^4 + p^2 + 1} </math> |
<math>~=</math> |
<math>~ \frac{x}{ z^{q^4p^2} }\biggl\{ \frac{\mathfrak{F_5}}{\lambda_5} \biggr\} \, , </math> |
we can also write,
|
<math>~\frac{\partial \lambda_5}{\partial x}</math> |
<math>~=</math> |
<math>~ - \frac{ z^{q^4p^2} }{x}\biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ 2q^4y^{2q^2} x^{p^2} + p^4 x^{2q^4}z^{p^2} \biggr] </math> |
Similarly,
|
<math>~\frac{\partial \lambda_5}{\partial y}</math> |
<math>~=</math> |
<math>~ \frac{2q^2}{y} \biggl( \frac{ y^{2q^2} }{ x^{2q^4} } \biggr) + \frac{q^2p^4}{y} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{ x^{2q^4} z^{q^4p^2} } \biggl[ \frac{2q^2}{y} \biggl( y^{2q^2} z^{q^4p^2} \biggr) + \frac{q^2p^4}{y} \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{x^{p^2}}{ y } \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ 2q^2 \biggl( y^{2q^2} z^{q^4p^2} \biggr) + q^2p^4 \biggl( y^{q^2p^4} x^{2q^4} \biggr)\biggr] \, ; </math> |
|
<math>~\frac{\partial \lambda_5}{\partial z}</math> |
<math>~=</math> |
<math>~ - \frac{q^4p^2}{z} \biggl( \frac{ y^{q^2p^4} }{ z^{q^4p^2} } \biggr) + \frac{p^4}{z} \biggl( \frac{ z^{p^4} }{ x^{p^2} } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ x^{p^2} z^{q^4p^2 }} \biggl[ \frac{p^4}{z} \biggl( z^{p^4+q^4p^2} \biggr) - \frac{q^4p^2}{z} \biggl( x^{p^2} y^{q^2p^4} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{x^{2q^4} }{z} \biggl\{ \frac{\lambda_5}{\mathfrak{F_5}} \biggr\} \biggl[ p^4 \biggl( z^{p^4 + q^4p^2 } \biggr) - q^4p^2 \biggl( x^{p^2} y^{q^2p^4} \biggr)\biggr] </math> |
Understanding the Volume Element
Let's see if the expression for the volume element makes sense; that is, does
|
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> |
<math>~=</math> |
<math>~dx dy dz \, ?</math> |
First, let's make sure that we understand how to relate the components of the Cartesian line element with the components of our T10 coordinates.
Line Element
MF53 claim that the following relation gives the various expressions for the scale factors; we will go ahead and incorporate the expectation that, since our coordinate system is orthogonal, the off-diagonal elements are zero.
|
<math>~ds^2 = dx^2 + dy^2 + dz^2</math> |
<math>~=</math> |
<math>~ \sum_{i=1,4,5} h_i^2 d\lambda_i^2 \, . </math> |
Let's see. The first term on the RHS is,
|
<math>~h_1^2 d\lambda_1^2</math> |
<math>~=</math> |
<math>~ h_1^2 \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)dx + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)dy + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)dz \biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~ h_1^2 \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 dx^2 + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 dy^2 + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 dz^2 </math> |
|
|
|
<math>~ + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dx~dy + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial z}\biggr)} dx~dz + \cancel{2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)} dy~dz \biggr] \, ; </math> |
the other two terms assume easily deduced, similar forms. When put together and after regrouping terms, we can write,
|
<math>~ \sum_{i=1,4,5} h_i^2 d\lambda_i^2 </math> |
<math>~=</math> |
<math>~ \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] dx^2 </math> |
|
|
|
<math>~ + \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggr] dy^2 </math> |
|
|
|
<math>~ + \biggl[ h_1^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggr] dz^2 \, . </math> |
Given that this summation should also equal the square of the Cartesian line element, <math>~(dx^2 + dy^2 + dz^2)</math>, we conclude that the three terms enclosed inside each of the pair of brackets must sum to unity. Specifically, from the coefficient of <math>~dx^2</math>, we can write,
|
<math>~h_1^2 \biggl( \frac{\partial \lambda_1}{\partial x}\biggr)^2 </math> |
<math>~=</math> |
<math>~ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \, . </math> |
Using this relation to replace <math>~h_1^2</math> in each of the other two bracketed expressions, we find for the coefficients of <math>~dy^2</math> and <math>~dz^2</math>, respectively,
|
<math>~\biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, ; </math> |
|
<math>~\biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggr] \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggr]\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \, . </math> |
We can use the first of these two expressions to solve for <math>~h_4^2</math> in terms of <math>~h_5^2</math>, namely,
|
<math>~\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_4^2\biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - h_4^2\biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
|
<math>~\Rightarrow ~~~ h_4^2 \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
Analogously, the second of these two expressions gives,
|
<math>~ h_4^2 \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} </math> |
Eliminating <math>~h_4</math> between the two gives the desired overall expression for <math>~h_5</math>, namely,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ - \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 + h_5^2 \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - h_5^2 \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ h_5^2 \biggl\{ \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 - \biggl( \frac{\partial \lambda_5}{\partial y}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ - \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 - \biggl( \frac{\partial \lambda_5}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] \biggr\} </math> |
|
|
|
<math>~ -\biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial y}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2\biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] </math> |
|
|
|
<math>~ + \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial z}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} - \biggl( \frac{\partial \lambda_4}{\partial x}\biggr)^2 \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ \biggl[ \gamma_{51}^2 \gamma_{12}^2 - \gamma_{52}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{43}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl[ \gamma_{51}^2 \gamma_{13}^2 - \gamma_{53}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{12}^2 \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{h_4^2 h_1^2}\biggl\{ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{43}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggl[ \gamma_{43}^2\gamma_{11}^2 -~ \gamma_{41}^2 \gamma_{13}^2 \biggr] - \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2 \gamma_{12}^2 \biggr] + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr)^2 \biggl[ \gamma_{42}^2 \gamma_{11}^2 - \gamma_{41}^2\gamma_{12}^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{h_5^2}{h_1^4 h_4^2 h_5^2}\biggl\{ \biggl[ \gamma_{51}^2 \gamma_{12}^2 - \gamma_{52}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43} \gamma_{11} - \gamma_{41} \gamma_{13} \biggr] - \biggl[ \gamma_{51}^2 \gamma_{13}^2 - \gamma_{53}^2 \gamma_{11}^2 \biggr] \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \biggl[ \gamma_{42} \gamma_{11} - \gamma_{41} \gamma_{12} \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{h_4^2 h_1^2}\biggl\{ \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43} \gamma_{11} - \gamma_{41} \gamma_{13} \biggr] - \biggl( \frac{\partial \lambda_1}{\partial y}\biggr)^2 \biggl[ \gamma_{43}\gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \biggl[ \gamma_{43}\gamma_{11} -~ \gamma_{41} \gamma_{13} \biggr] - \biggl( \frac{\partial \lambda_1}{\partial x} \biggr)^{2} \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \biggl[ \gamma_{42} \gamma_{11} - \gamma_{41} \gamma_{12} \biggr]
|
|
|
<math>~=</math> |
<math>~ \frac{1}{h_1^4 h_4^2 }\biggl\{ - \biggl[ \gamma_{51} \gamma_{12} + \gamma_{52} \gamma_{11} \biggr] \gamma_{43} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr] \gamma_{52} + \biggl[ \gamma_{51} \gamma_{13} + \gamma_{53} \gamma_{11} \biggr] \gamma_{42} \biggl[ \gamma_{42} \gamma_{11} + \gamma_{41} \gamma_{12} \biggr] \gamma_{53} \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{ h_1^4 h_4^2}\biggl\{ \gamma_{12}^2 \biggl[ \gamma_{43}\gamma_{11} + \gamma_{41} \gamma_{13} \biggr]\gamma_{52} -\gamma_{11}^{2} \biggl[ \gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} \biggr]\gamma_{52}
|
|
|
<math>~=</math> |
<math>~ \frac{1}{h_1^4 h_4^2 }\biggl\{ \biggl[ (- \gamma_{51} \gamma_{12} - \gamma_{52} \gamma_{11} ) \gamma_{43} + \gamma_{12}^2 -\gamma_{11}^{2} \biggr] (\gamma_{43} \gamma_{11} + \gamma_{41} \gamma_{13} ) \gamma_{52} + \biggl[ (\gamma_{51} \gamma_{13} + \gamma_{53} \gamma_{11} ) \gamma_{42} - \gamma_{11}^{2} + \gamma_{13}^2 \biggr] (\gamma_{42} \gamma_{11} + \gamma_{41}\gamma_{12} ) \gamma_{53} \biggr\} </math> |
… Not sure this is headed anywhere useful!
Volume Element
|
<math>~(h_1 h_4 h_5) d\lambda_1 d\lambda_4 d\lambda_5</math> |
<math>~=</math> |
<math>~ (h_1 h_4 h_5) \biggl[ \biggl( \frac{\partial \lambda_1}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_1}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_1}{\partial z}\biggr) dz \biggr] \biggl[ \biggl( \frac{\partial \lambda_4}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_4}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_4}{\partial z}\biggr) dz \biggr] \biggl[ \biggl( \frac{\partial \lambda_5}{\partial x}\biggr) dx + \biggl( \frac{\partial \lambda_5}{\partial y}\biggr) dy + \biggl( \frac{\partial \lambda_5}{\partial z}\biggr) dz \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \gamma_{11}\biggr) dx + \biggl( \gamma_{12}\biggr) dy + \biggl( \gamma_{13}\biggr) dz \biggr] \biggl[ \biggl( \gamma_{41}\biggr) dx + \biggl( \gamma_{42}\biggr) dy + \biggl( \gamma_{43}\biggr) dz \biggr] \biggl[ \biggl( \gamma_{51} \biggr) dx + \biggl( \gamma_{52} \biggr) dy + \biggl( \gamma_{53} \biggr) dz \biggr] </math> |
COLLADA
Here we try to use the 3D-visualization capabilities of COLLADA to test whether or not the three coordinates associated with the T6 Coordinate system are indeed orthogonal to one another. We begin by making a copy of the Inertial17.dae text file, which we obtain from an accompanying discussion. When viewed with the Mac's Preview application, this group of COLLADA-based instructions displays a purple ellipsoid with axis ratios, (b/a, c/a) = (0.41, 0.385). This means that we are dealing with an ellipsoid for which,
|
<math>~q \equiv \frac{a}{b}</math> |
<math>~=</math> |
<math>~2.44</math> |
and, |
<math>~p \equiv \frac{a}{c}</math> |
<math>~=</math> |
<math>~2.60 \, .</math> |
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ;</math> |
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, ; </math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, ;</math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
First Trial
| First Trial (specified variable values have bgcolor="pink") |
|||||
| x | y | z | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.5 | 0.35493 | 0.00000 | 1 | 0.46052 | 2.11310 |
Unit Vectors
|
<math>~\hat{e}_1 </math> |
<math>~=</math> |
<math>~ \hat\imath (x_0 \ell_{3D}) + \hat\jmath (q^2y_0 \ell_{3D}) + \hat{k} (p^2 z_0 \ell_{3D}) </math> |
|
|
<math>~=</math> |
<math>~ \hat\imath (0.23026) + \hat\jmath (0.97313) \, ; </math> |
|
<math>~\hat{e}_2</math> |
<math>~=</math> |
<math>~ \frac{x_0 q^2 y_0 p^2 z_0}{\mathcal{D}} \biggl\{ \hat{\imath} \biggl( \frac{1}{x_0} \biggr) + \hat{\jmath} \biggl( \frac{1}{q^2 y_0} \biggr) + \hat{k} \biggl( -\frac{2}{p^2 z_0} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-\hat{k} ~\biggl( \frac{2x_0 q^2 y_0 }{\mathcal{D}} \biggr) </math> |
|
|
<math>~=</math> |
<math>~-\hat{k} ~\biggl( 1 \biggr) \ ; </math> |
|
<math>~\hat{e}_3 </math> |
<math>~=</math> |
<math>~\frac{\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath \biggl[ x_0(2 q^4y_0^2 + p^4z_0^2 ) \biggl] + \hat\jmath \biggl[ q^2 y_0(p^4z_0^2 + 2x_0^2 ) \biggl] + \hat{k} \biggl[ p^2z_0( x_0^2 - q^4y_0^2 ) \biggl] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2q^2 x_0 y_0\ell_{3D}}{\mathcal{D}} \biggl\{ -\hat\imath ( q^2y_0 ) + \hat\jmath (x_0) \biggr\} = \biggl(1\biggr)\ell_{3D}\biggl\{ -\hat\imath ( q^2y_0 ) + \hat\jmath (x_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\hat\imath (0.97313 ) + \hat\jmath (0.23026) \, . </math> |
Tangent Plane
From our above derivation, the plane that is tangent to the ellipsoid's surface at <math>~(x_0, y_0, z_0)</math> is given by the expression,
|
<math>~ x x_0 + q^2 y y_0 + p^2 z z_0 </math> |
<math>~=</math> |
<math>~ (\lambda_1^2)_0 \, . </math> |
For this First Trial, we have (for all values of <math>~z</math>, given that <math>~z_0 = 0</math>) …
|
<math>~ (0.5)x + (2.11310)y </math> |
<math>~=</math> |
<math>~ 1 </math> |
|
<math>~\Rightarrow ~~~ y </math> |
<math>~=</math> |
<math>~ \frac{(1 - 0.5x)}{2.11310} \, . </math> |
So let's plot a segment of the tangent plane whose four corners are given by the coordinates,
| Corner | x | y | z |
| A | x_0 - 0.25 = +0.25 | 0.41408 | -0.25 |
| B | x_0 + 0.25 = +0.75 | 0.29577 | -0.25 |
| C | x_0 - 0.25 = +0.25 | 0.41408 | +0.25 |
| D | x_0 + 0.25 = +0.75 | 0.29577 | +0.25 |
Now, in order to give some thickness to this tangent-plane, let's adjust the four corner locations by a distance of <math>~\pm 0.1</math> in the <math>~\hat{e}_1</math> direction.
Eight Corners of Tangent Plane
Corner 1: Shift surface-point location <math>~(x_0, y_0, z_0)</math> by <math>~(+\Delta e_1)</math> in the <math>~\hat{e}_1</math> direction, by <math>~(+\Delta e_2)</math> in the <math>~\hat{e}_2</math> direction, and by by <math>~(+\Delta e_3)</math> in the <math>~\hat{e}_3</math> direction. This gives …
|
<math>~x_1</math> |
<math>~=</math> |
<math>~x_0 + (\Delta e_1)0.23026 - (\Delta e_2)0.97313</math> |
Second Trial
| Second Trial … <math>~(q = 2.44, p = 2.60)</math> [specified variable values have bgcolor="pink"] |
|||||
| x_0 | y_0 | z_0 | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.5 | 0.35493 | 0.00000 | 1 | 0.46052 | 2.11310 |
Generic Unit Vector Expressions
Let's adopt the notation,
|
<math>~\hat{e}_i</math> |
<math>~=</math> |
<math>~\hat\imath ~[e_{ix}] + \hat\jmath ~[e_{iy}] + \hat{k} ~[e_{iz}]</math> |
for, | <math>~i = 1,3 \, .</math> |
Then, for the T6 Coordinate system, we have,
|
<math>~e_{1x}</math> |
<math>~\equiv</math> |
<math>~x_0 \ell_{3D} \, ;</math> |
<math>~e_{1y}</math> |
<math>~\equiv</math> |
<math>~q^2y_0 \ell_{3D} \, ;</math> |
<math>~e_{1z}</math> |
<math>~\equiv</math> |
<math>~p^2 z_0 \ell_{3D} \, ;</math> |
||
|
<math>~e_{2x}</math> |
<math>~\equiv</math> |
<math>~ \frac{q^2 y_0 p^2 z_0}{\mathcal{D}}\, ;</math> |
<math>~e_{2y}</math> |
<math>~\equiv</math> |
<math>~\frac{x_0 p^2 z_0}{\mathcal{D}} \, ;</math> |
<math>~e_{2z}</math> |
<math>~\equiv</math> |
<math>~- \frac{2x_0 q^2 y_0}{\mathcal{D}}\, ;</math> |
||
|
<math>~e_{3x}</math> |
<math>~\equiv</math> |
<math>~-x_0(2 q^4y_0^2 + p^4z_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3y}</math> |
<math>~\equiv</math> |
<math>~q^2 y_0(p^4z_0^2 + 2x_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3z}</math> |
<math>~\equiv</math> |
<math>~p^2z_0( x_0^2 - q^4y_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, .</math> |
| Second Trial | |||
| x | y | z | |
| <math>~e_1</math> | 0.23026 | 0.97313 | 0.0 |
| <math>~e_2</math> | 0.0 | 0.0 | -1.0 |
| <math>~e_3</math> | - 0.97313 | 0.23026 | 0.0 |
What are the coordinates of the eight corners of a thin tangent-plane? Let's say that we want the plane to extend …
- From <math>~(-\Delta_1)</math> to <math>~(+\Delta_1)</math> in the <math>~\hat{e}_1</math> direction … here we set <math>~\Delta_1 = 0.05</math>;
- From <math>~(-\Delta_2)</math> to <math>~(+\Delta_2)</math> in the <math>~\hat{e}_2</math> direction … here we set <math>~\Delta_2 = 0.25</math>;
- From <math>~(-\Delta_3)</math> to <math>~(+\Delta_3)</math> in the <math>~\hat{e}_3</math> direction … here we set <math>~\Delta_3 = 0.25</math>.
|
<math>~\Delta_x</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1x} + \Delta_2 e_{2x} + \Delta_3 e_{3x} = -0.23177 \, ;</math> |
|
<math>~\Delta_y</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1y} + \Delta_2 e_{2y} + \Delta_3 e_{3y} = +0.10622 \, ;</math> |
|
<math>~\Delta_z</math> |
<math>~=</math> |
<math>~\Delta_1 e_{1z} + \Delta_2 e_{2z} + \Delta_3 e_{3z} = -0.25000 \, .</math> |
Third Trial
GoodPlane01
| Third Trial … <math>~(q = 2.44, p = 2.60)</math> [specified variable values have bgcolor="pink"] |
|||||
| x_0 | y_0 | z_0 | <math>~\lambda_1</math> | <math>~\ell_{3D}</math> | <math>~\mathcal{D}</math> |
| 0.8 | 0.24600 | 0.00000 | 1 | 0.59959 | 2.34146 |
Again, for the T6 Coordinate system, we have,
|
<math>~e_{1x}</math> |
<math>~\equiv</math> |
<math>~x_0 \ell_{3D} \, ;</math> |
<math>~e_{1y}</math> |
<math>~\equiv</math> |
<math>~q^2y_0 \ell_{3D} \, ;</math> |
<math>~e_{1z}</math> |
<math>~\equiv</math> |
<math>~p^2 z_0 \ell_{3D} \, ;</math> |
||
|
<math>~e_{2x}</math> |
<math>~\equiv</math> |
<math>~ \frac{q^2 y_0 p^2 z_0}{\mathcal{D}}\, ;</math> |
<math>~e_{2y}</math> |
<math>~\equiv</math> |
<math>~\frac{x_0 p^2 z_0}{\mathcal{D}} \, ;</math> |
<math>~e_{2z}</math> |
<math>~\equiv</math> |
<math>~- \frac{2x_0 q^2 y_0}{\mathcal{D}}\, ;</math> |
||
|
<math>~e_{3x}</math> |
<math>~\equiv</math> |
<math>~-x_0(2 q^4y_0^2 + p^4z_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3y}</math> |
<math>~\equiv</math> |
<math>~q^2 y_0(p^4z_0^2 + 2x_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, ;</math> |
<math>~e_{3z}</math> |
<math>~\equiv</math> |
<math>~p^2z_0( x_0^2 - q^4y_0^2 )\frac{\ell_{3D}}{\mathcal{D}} \, .</math> |
| Third Trial | ||||
| x | y | z | <math>~\Delta_\mathrm{TP}</math> | |
| <math>~e_1</math> | 0.47967 | 0.87745 | 0.0 | 0.02 |
| <math>~e_2</math> | 0.0 | 0.0 | -1.0 | 0.25 |
| <math>~e_3</math> | - 0.87753 | 0.47952 | 0.0 | 0.25 |
In constructing the Tangent-Plane (TP) for a 3D COLLADA display, we first move from the point that is on the surface of the ellipsoid, <math>~\vec{x}_0 = (x_0, y_0, z_0) = (0.8, 0.246, 0.0)</math>, to
| vertex "m" |
<math>~\vec{P}_m</math> | Components | ||
| <math>~x_m = \hat\imath \cdot \vec{P}_m</math> | <math>~y_m = \hat\jmath \cdot \vec{P}_m</math> | <math>~z_m = \hat{k} \cdot \vec{P}_m</math> | ||
| 0 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 - \Delta_2\hat{e}_2 - \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} - \Delta_2 e_{2x} - \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} - \Delta_2 e_{2y} - \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} - \Delta_2 e_{2z} - \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) - 0.25 (-0.87752) = 1.00979 |
0.24590 - 0.02 (0.87753) - 0.25 (0.47952) = 0.10847 |
- 0.25 (-1.0) = + 0.25 |
||
| 1 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 + \Delta_2\hat{e}_2 - \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} + \Delta_2 e_{2x} - \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} + \Delta_2 e_{2y} - \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} + \Delta_2 e_{2z} - \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) - 0.25 (-0.87752) = 1.00979 |
0.24590 - 0.02 (0.87753) - 0.25 (0.47952) = 0.10847 |
+ 0.25 (-1.0) = - 0.25 |
||
| 2 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 - \Delta_2\hat{e}_2 + \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} - \Delta_2 e_{2x} + \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} - \Delta_2 e_{2y} + \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} - \Delta_2 e_{2z} + \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) + 0.25 (-0.87752) = 0.56307 |
0.24590 - 0.02 (0.87753) + 0.25 (0.47952) = 0.34823 |
- 0.25 (-1.0) = + 0.25 |
||
| 3 | <math>~\vec{x}_0 - \Delta_1\hat{e}_1 + \Delta_2\hat{e}_2 + \Delta_3\hat{e}_3</math> |
<math>~ x_0 - \Delta_1 e_{1x} + \Delta_2 e_{2x} + \Delta_3 e_{3x} </math> |
<math>~ y_0 - \Delta_1 e_{1y} + \Delta_2 e_{2y} + \Delta_3 e_{3y} </math> |
<math>~ z_0 - \Delta_1 e_{1z} + \Delta_2 e_{2z} + \Delta_3 e_{3z} </math> |
|
0.8 - 0.02 (0.47952) + 0.25 (-0.87752) = 0.57103 |
0.24590 - 0.02 (0.87753) + 0.25 (0.47952) = 0.34823 |
+ 0.25 (-1.0) = - 0.25 |
||
| 4 |
0.8 + 0.02 (0.47952) - 0.25 (-0.87752) = 1.0290 |
0.24590 + 0.02 (0.87753) - 0.25 (0.47952) = 0.1436 |
- 0.25 (-1.0) = + 0.25 |
|
| 5 |
0.8 + 0.02 (0.47952) - 0.25 (-0.87752) = 1.0290 |
0.24590 + 0.02 (0.87753) - 0.25 (0.47952) = 0.1436 |
+ 0.25 (-1.0) = - 0.25 |
|
| 6 |
0.8 + 0.02 (0.47952) + 0.25 (-0.87752) = 0.59021 |
0.24590 + 0.02 (0.87753) + 0.25 (0.47952) = 0.38333 |
- 0.25 (-1.0) = + 0.25 |
|
| 7 |
0.8 + 0.02 (0.47952) + 0.25 (-0.87752) = 0.59021 |
0.24590 + 0.02 (0.87753) + 0.25 (0.47952) = 0.38333 |
+ 0.25 (-1.0) = - 0.25 |
|
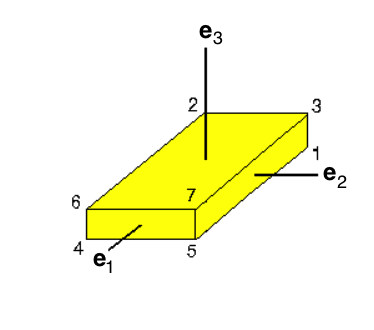 |
 |
| <math>~x_0 = 0.8, z_0 = 0.0, y_0 = 0.246, \lambda_1 = 1.0</math> | |
 |
|
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | |
GoodPlane02
| <math>~x_0 = 0.075, z_0 = 0.0, y_0 = 0.4089, \lambda_1 = 1.0</math> | |
 |
|
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | |
GoodPlane03
| <math>~x_0 = 0.25, z_0 = 0.20, y_0 = 0.33501, \lambda_1 = 1.0</math> | |
 |
 |
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.25, \Delta_3 = 0.25</math> | <math>~\Delta_1 = 0.02, \Delta_2 = 0.10, \Delta_3 = 0.25</math> |
|
CAPTION: The image on the right differs from the image on the left in only one way — <math>~\Delta_2</math> = 0.1 instead of 0.25. It illustrates more clearly that the <math>~\hat{e}_3</math> (longest) coordinate axis is not parallel to the z-axis when <math>~z_0 \ne 0.</math> |
|
GoodPlane04
| <math>~x_0 = 0.25, z_0 = 1/3, y_0 = 0.1777, \lambda_1 = 1.0</math> |
 |
| <math>~\Delta_1 = 0.02, \Delta_2 = 0.10, \Delta_3 = 0.25</math> |
Further Exploration
Let's set: <math>~x_0 = 0.25, y_0 = 0.33501, z_0 = 0.2 ~~~\Rightarrow ~~~\lambda_1 = 1.00000, \lambda_2 = 0.33521 \, .</math>
|
<math>~q \equiv \frac{a}{b}</math> |
<math>~=</math> |
<math>~2.43972</math> |
and, |
<math>~p \equiv \frac{a}{c}</math> |
<math>~=</math> |
<math>~2.5974 \, .</math> |
|
<math>~\lambda_1</math> |
<math>~\equiv</math> |
<math>~(x^2 + q^2 y^2 + p^2 z^2)^{1 / 2} \, ;</math> |
|
<math>~\lambda_2</math> |
<math>~=</math> |
<math>~ \frac{x y^{1/q^2}}{ z^{2/p^2}} \, ; </math> |
|
<math>~\ell_{3D}</math> |
<math>~\equiv</math> |
<math>~\biggl[ x^2 + q^4y^2 + p^4 z^2 \biggr]^{- 1 / 2} \, ;</math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~(q^4 y^2 p^4 z^2 + x^2 p^4 z^2 + 4x^2q^4y^2)^{1 / 2} \, .</math> |
Next, let's examine the curve that results from varying <math>~z</math> while <math>~\lambda_1</math> and <math>~\lambda_2</math> are held fixed. From the expression for <math>~\lambda_2</math> we appreciate that,
|
<math>~x</math> |
<math>~=</math> |
<math>~\frac{\lambda_2 z^{2/p^2}}{y^{1/q^2}} \, ;</math> |
and from the expression for <math>~\lambda_1</math> we have,
|
<math>~x^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - q^2y^2 - p^2z^2 \, .</math> |
Hence, the relationship between <math>~y</math> and <math>~z</math> is,
|
<math>~\biggl[ \frac{\lambda_2 z^{2/p^2}}{y^{1/q^2}} \biggr]^2</math> |
<math>~=</math> |
<math>~\lambda_1^2 - q^2y^2 - p^2z^2</math> |
|
<math>~\Rightarrow ~~~ \lambda_2^2 z^{4/p^2} </math> |
<math>~=</math> |
<math>~y^{2/q^2} \biggl[ \lambda_1^2 - q^2y^2 - p^2z^2\biggr] \, .</math> |
|
Alternatively,
Hence, the relationship between <math>~x</math> and <math>~z</math> is,
|
Here are some example values …
| <math>~\lambda_1 = 1</math> and, <math>~\lambda_2 = 0.33521</math> | ||||||
| <math>~z</math> | 1st Solution | 2nd Solution |  |
|||
| <math>~y_1</math> | <math>~x_1</math> | <math>~y_2</math> | <math>~x_2</math> | |||
| 0.01 | 0.407825695 | 0.0995168 | - | - | ||
| 0.03 | 0.40481851 | 0.138 | - | - | ||
| 0.04 | 0.40309223 | 0.1503934 | - | - | ||
| 0.08 | 0.393779065 | 0.1854283 | - | - | ||
| 0.12 | 0.37990705 | 0.2103761 | - | - | ||
| 0.16 | 0.36067787 | 0.23111 | 1.04123×10-4 | 0.9095546 | ||
| 0.2 | 0.33500747 | 0.2500033 | 2.23778×10-4 | 0.85448 | ||
| 0.22 | 0.31923525 | 0.2592611 | 3.36653 ×10-4 | 0.82065 | ||
| 0.24 | 0.30106924 | 0.2686685 | 5.2327 ×10-4 | 0.78192 | ||
| 0.26 | 0.2799962 | 0.2784963 | 8.53243 ×10-4 | 0.73752 | ||
| 0.28 | 0.25521147 | 0.2891526 | 1.491545 ×10-3 | 0.68634 | ||
| 0.3 | 0.22530908 | 0.3013752 | 2.89262 ×10-3 | 0.62671 | ||
| 0.32 | 0.1873233 | 0.3168808 | 6.6223 ×10-3 | 0.55579 | ||
| 0.34 | 0.13149897 | 0.3423994 | 2.09221 ×10-2 | 0.46637 | ||
| 0.343 | 0.1191543 | 0.3490285 | 0.026458 | 0.4496 | ||
| 0.344 | 0.1145 | 0.3517 | 0.02880 | 0.4435 | ||
| 0.345 | 0.1093972 | 0.354688 | 0.03155965 | 0.4371186 | ||
| 0.3485 | 0.0847372 | 0.3713588 | 0.0480478 | 0.4085204 | ||
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |