User:Tohline/Appendix/Ramblings/BordeauxPostDefense
Université de Bordeaux (Part 3)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Discussions Following Dissertation Defense
Shapes
Jean-Marc's Question to Joel Regarding Shapes
When you ask about topological changes around Ansorg's solution, did you mean for instance the change in the shape of the two bodies, with rounded edges, and slightly less oblate spheroid and ring, or something else ?
Joel's Initial Response Regarding Shapes
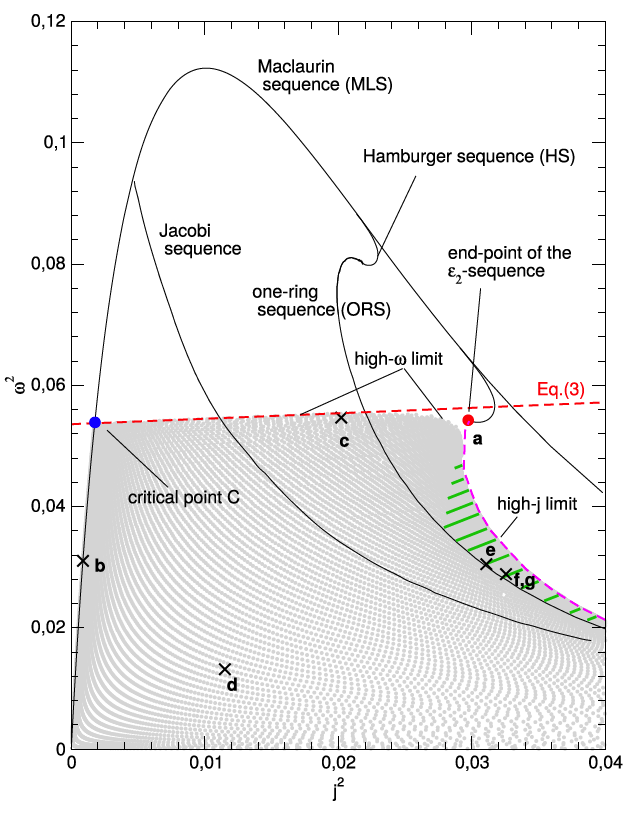
My "shape" question was in the context of especially Figures 4.6 and 4.7 (pp. 81 - 82) in Baptiste's dissertation. I was interested to hear Baptiste elaborate on his sentence near the top of p. 83: "The effect of binarity tends to modify the shape with respect to single body figures." Focusing on the central "spheroid", it seems clear that a (non-differentiable?) cusp appears at the surface of the spheroid in the configuration that marks the end of the M. Ansorg, A. Kleinwächter & R. Meinel (2003) sequence. I presume that **just past** this critical model, as the spheroid becomes detached from the surrounding ring, the surface of the spheroid is everywhere smooth (contains no cusp). I was curious to know (from Baptiste) whether he had closely examined this "detachment".
(A) There must be a local effective-potential maximum in the equatorial plane; where is this maximum with respect to the location of the cusp? And where is it located immediately after detachment; is it in the "gap", or is it located inside one of the two objects?
(B) I was also curious to know whether the **mathematical** topological transition -- from a single, distorted object to a detached pair -- is in any way reflected in the **physics** of the system at this critical point along the model sequence. (This is potentially a crazy question, but I was nevertheless curious how Baptiste would respond to it.)
Further elaboration … Off and on over the past few decades I have given some thought to a closely related example of topological-transition. If a binary system is to form from the "fission" of a rotating ellipsoidal (or dumb-bell-shaped) configuration, then that will also involve a transition from a figure whose surface encloses a single object and (suddenly?) to a figure whose surface encloses two disconnected objects. As we attempt to model the time-dependent processes associated with binary fission, a discussion of topological transition is likely to be most relevant — if at all — in the case of incompressible fluids because shape evolution can be reduced to a 2D-surface (rather than 3D volume) problem.
NOTE: Even though I have **thought** about this issue in the past, I have not made any concrete progress. Perhaps an approach along the following lines is relevant: S. W. Walker (2007) — A hybrid variational-level set approach to handle topological changes
In the context of Baptiste's axisymmetric models, the relevant technical hurdles might be reduced even further because, presumably, the shape evolution can be reduced to a 1D problem. Someone ought to be able to write down the set of time-dependent "1D" equations (for the surface of an axisymmetric, incompressible fluid) that would allow us to follow the evolution of a spheroidal configuration as it makes a transition to a spheroid/ring system.
Fission Hypothesis (Joel's Thoughts)
|
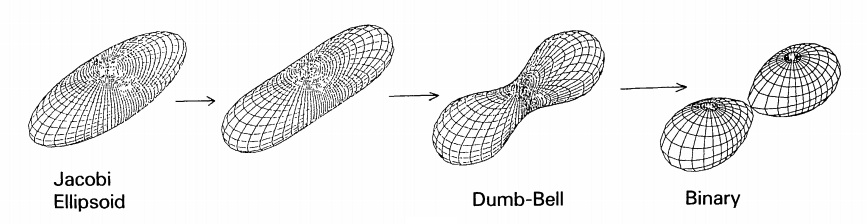
Throughout my research career, the question that has most intrigued me is, "How do binary stars form?" A close second is the question, "Does the classic fission hypothesis properly describe how — at least some if not all — binary stars form?" In an accompanying chapter I have provided a small collection of images — from diverse scientific & engineering disciplines — that always come to mind when I think about, or discuss with others the concept of, fission.
The figure from Hachisu & Eriguchi (1984) that is reprinted here on the left, provides a rigorous foundation for discussions of fission (and binary star formation) in the context of astrophysics. Each of the pictured configurations shows the surface (shape) of an incompressible fluid model whose detailed force-balanced equilibrium structure can be specified precisely. And while we can identify where each of these configurations is located along a precisely defined equilibrium sequence — along, for example, the Jacobi ellipsoid sequence or the Dumbbell-Binary sequence — time is completely absent from the picture. Well … the arrows in the figure suggest how evolution from one configuration to the next might occur. But we [i.e., the astrophysics community] have not yet been able to simulate in a quantitatively robust manner how any one of these fluid configurations evolves toward any other one of the configurations. I have always hoped that the community will develop the technical tools that will allow us to perform such time-evolutionary simulations, and that I would be able to make a meaningful contribution to these efforts. But we have not yet succeeded in this task.
As the community attempts to simulate the time-dependent evolution of these and related self-gravitating fluid systems, should we focus on incompressible fluids (such as the ones depicted in the Hichisu & Eriguchi figure), or should our focus be on incompressible fluids?
COMPRESSIBLE FLUIDS: The physical properties of protostellar gas clouds are not well described by an incompressible (n = 0 polytropic) equation of state. Ideally, then, our attempt to simulate fission should focus on modeling the evolution of self-gravitating fluids that obey a compressible equation of state (EOS) — for example, polytopes with n ≥ 1. This is why, over the years, my research group has invested a great deal of time developing numerical techniques that can be used to accurately (a) construct initial equilibrium models, and (b) follow the subsequent dynamical evolution, of rapidly rotating, compressible fluid systems. Generally speaking, step "a" has involved implementation of the HSCF technique, while step "b" has involved the development of finite-volume techniques to solve the coupled set of Principle Governing Equations supplemented by a compressible, polytropic EOS.
incorporate simulation of we should therefore So, ideally, best described by compressible equations of state.
GOOD NEWS & BAD NEWS:
- The equilibrium structures displayed by Hachisu & Eriguchi (1984) are uniform-density, incompressible fluids. Oscillation frequencies are known for many of these systems, which means that points of instability can be identified along with growth rates in the linear regime.
Physical Meaning of High-Omega Limit
Jean-Marc's Question to Joel Regarding Limit
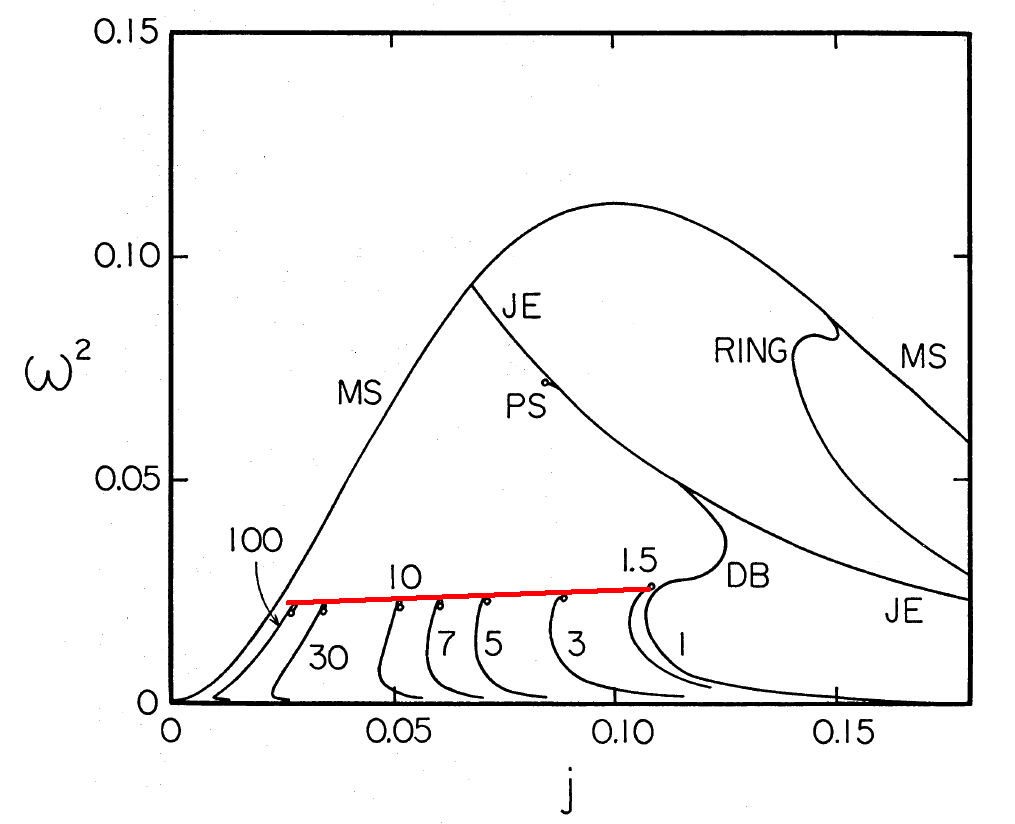
Also, about the Eriguchi and Hachisu (EH) 's line ending the binary sequence, I missed one point. This line gathers the end of sequences obtained for various mass ratios, but it seems to me that all this sequences share the same (unity) constrast density between the two components (eta=1), which means that the mass density is the same for the two bodies, while the mass ratios differ, am I right ? Then, isn't the high-omega limit in Baptiste's graph some kind of analogous to EH's line for binaries ? What is it your question ?
Joel's Initial Response Regarding Shapes
Regarding the EH binary sequences: Yes, I agree with your description of the situation ... "the high-omega limit in Baptiste's graph is analogous to EH's (limiting) line for binaries." (Immediately below, I have displayed the relevant EH plot; in red ink, I have hand-drawn the relevant limiting line.) My question is, "What gives rise to this locus of termination points in both types of physical systems?" EH argue convincingly that, in the binary case, each termination point is related to the classic Roche limit. In the EH paper, it is easy to see this because they explicitly plot individual (constant mass ratio) model sequences. My guess is that Baptiste's high-omega limit is also a locus of termination points, but for an **axisymmetric** Roche problem. Did he ever plot individual model sequences (for his axisymmetric configurations) that would be analogous to the EH model sequences (for binaries)?
I am interested in this issue, in part, because some time ago — in collaboration with two LSU students — I attempted to analyze some aspects of the "axisymmetric Roche problem." [See J. W. Woodward, S. Sankaran, & J. E. Tohline (1992).] I would now be very interested in figuring out the overlap that this simple analysis has with Baptiste's much more rigorous investigation.
|
|
See Also
- Université de Bordeaux (Part 1): External Gravitational Potential of Toroids
- Université de Bordeaux (Part 2): Spheroid-Ring Sequences

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |