Embedded Polytropic Spheres

In a separate discussion we showed how to determine the structure of isolated polytropic spheres. These are rather idealized stellar structures in which the pressure and density both drop to zero at the surface of the star. Here we consider how the equilibrium radius of a polytropic configuration of a given <math>M</math> and <math>~K_\mathrm{n}</math> is modified when it is embedded in an external medium of pressure <math>P_e</math>. We will begin by focusing on polytropes of index <math>~n</math> = 1 and <math>~n</math> = 5 because their structures can be described by analytic mathematical expressions.

<math>~n</math> = 1 Polytrope

Drawing from the earlier discussion of isolated polytropes, we will reference various radial locations within the spherical configuration by the dimensionless radius,

<math> \xi \equiv \frac{r}{a_\mathrm{n=1}} , </math>

where,

<math> a_\mathrm{n=1} \equiv \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)_{n=1}\biggr]^{1/2} = \biggl[\frac{K}{2\pi G} \biggr]^{1/2} \, . </math>

Review

Again, from the earlier discussion, we can describe the properties of an isolated, spherical <math>~n</math> = 1 polytrope as follows:

Mass:

In terms of the central density, <math>\rho_c</math>, and <math>~K_\mathrm{n}</math>, the total mass is,

<math>M = \frac{4}{\pi} \rho_c (\pi a_{n=1})^3 = 4\pi^2 \rho_c \biggl[\frac{K}{2\pi G} \biggr]^{3/2} = \rho_c \biggl[\frac{2\pi K^3}{G^3} \biggr]^{1/2}</math> ;

and, expressed as a function of <math>M</math>, the mass that lies interior to the dimensionless radius <math>\xi</math> is,

<math>\frac{M_\xi}{M} = \frac{1}{\pi} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, ,~~~~~~\mathrm{for}~\pi \ge \xi \ge 0 \, .</math>

Hence,

<math>M_\xi = \rho_c \biggl[\frac{2K^3}{\pi G^3} \biggr]^{1/2} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, .</math>

Pressure:

The central pressure of the configuration is,

<math>P_c = \biggl[ \frac{G^3}{2\pi} \rho_c^4 M^2 \biggr]^{1/3} = \biggl[ \frac{G^3}{2\pi} \rho_c^6 \biggl(\frac{2\pi K^3}{G^3} \biggr) \biggr]^{1/3} = K\rho_c^2</math> ;

and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,

<math>P_\xi= P_c \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .

Hence,

<math>P_\xi= K\rho_c^2 \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .

Extension to Bounded Sphere

Eliminating <math>\rho_c</math> between the last expression for <math>M_\xi</math> and the last expression for <math>P_\xi</math> gives,

<math>P_\xi= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M_\xi^2}{K^2} \biggr] \biggl[ \frac{\sin\xi}{\xi(\sin\xi - \xi \cos\xi )} \biggr]^2</math> .

Now, if we rip off an outer layer of the star down to some dimensionless radius <math>\xi_e < \pi</math>, the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should remain in equilibrium if we impose the appropriate amount of externally applied pressure <math>P_e = P_{\xi_e} </math> at that radius. (This will work only for spherically symmetric configurations, as the gravitation acceleration at any location only depends on the mass contained inside that radius.) If we rescale our solution such that the mass enclosed within <math>\xi_e</math> is the original total mass <math>M</math>, then the pressure that must be imposed by the external medium in which the configuration is embedded is,

<math>P_e= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M^2}{K^2} \biggr] \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2</math> .

The associated equilibrium radius of this pressure-confined configuration is,

<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=1} = \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e </math>

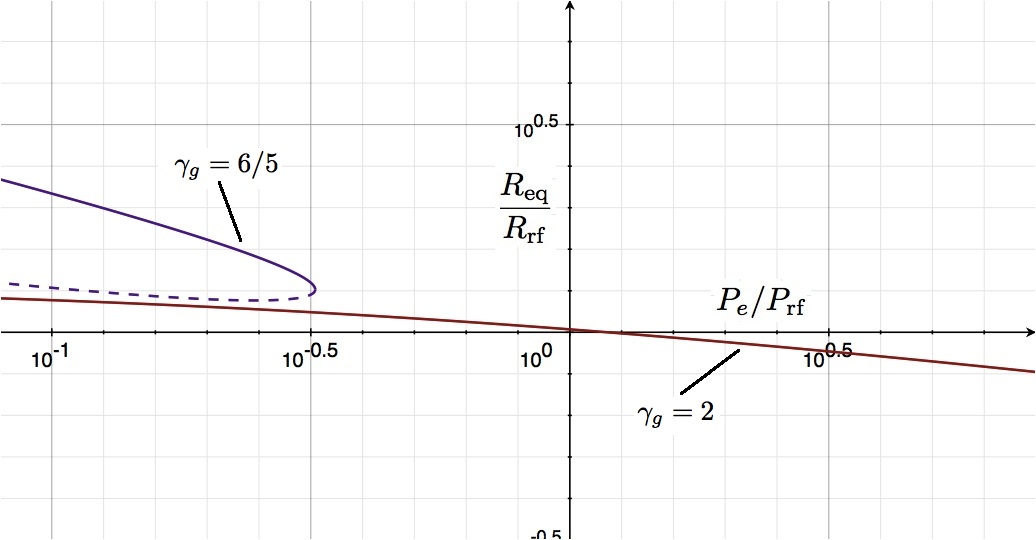
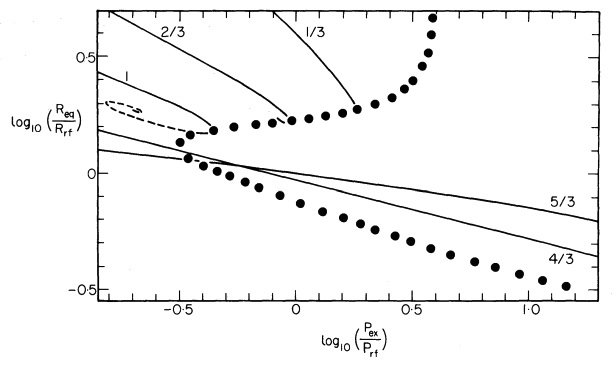
The solid black curve in Figure 1 shows how <math>R_\mathrm{eq}</math> varies with the applied external pressure <math>P_e</math>. Following the lead of Whitworth (1981, MNRAS, 195, 967), these two quantities have been respectively normalized (or, "referenced") to,

<math> R_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \biggl( \frac{3^2 \cdot 5}{2^4 \pi} \biggr)^{1/2} \biggl(\frac{K}{G}\biggr)^{1/2} ~~~\Rightarrow ~~~ \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{2^3}{3^2 \cdot 5} \biggr)^{1/2} \xi_e \, ; </math>

and,

<math> P_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \frac{2^6 \pi}{3^4 \cdot 5^3} \biggl(\frac{G^3 M^2}{K^2}\biggr) ~~~\Rightarrow ~~~ \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{3^4 \cdot 5^3}{2^7} \biggr) \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 \, . </math>

Figure 1: Equilibrium R-P Diagram

Top: The solid curve shows how the equilibrium radius <math>(R_\mathrm{eq})</math> of an n = 1 <math>(\gamma_g = 2)</math> polytrope varies with applied external pressure, <math>P_e</math>. Logarithmic units are used along both axes; <math>P_e</math> is normalized to <math>P_\mathrm{rf}</math> and <math>R_\mathrm{eq}</math> is normalized to <math>R_\mathrm{rf}</math>, as defined in the text.

Bottom: A reproduction of Figure 1b from Whitworth (1981, MNRAS, 195, 967). The various curves identify the equilibrium radii, <math>R_\mathrm{eq}</math>, that result from embedding polytropic structures with various effective adiabatic indexes <math>(\gamma_g = 1/3,~ 2/3,~ 1,~ 4/3,~ 5/3)</math> in an external medium of pressure <math>P_\mathrm{ex}</math>.

Comparison: The analytically derived solution for n = 1 <math>(\gamma_g = 2)</math>, shown above, that traces out <math>\chi_1(\Pi)</math> and <math>\chi_2(\Pi)</math> should be identical to this "Whitworth" curve labeled "1".

<math>~n</math> = 5 Polytrope

To derive the radial distribution of the Lane-Emden function <math>\Theta_H(r)</math> for an <math>~n</math> = 5 polytrope, we must solve,

<math>\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - (\Theta_H)^5</math> ,

subject to the above-specified boundary conditions. Following Emden (1907), C67 (pp. 93-94) shows that by making the substitutions,

<math> \xi = \frac{1}{x} = e^{-t} \, ; ~~~~~\Theta_H = \biggl(\frac{x}{2}\biggr)^{1/2} z = \biggl(\frac{1}{2}e^t\biggr)^{1/2}z \, , </math>

the differential equation can be rewritten as,

This equation has the solution,

<math> z = \pm \biggl[ \frac{12 C e^{-2t}}{(1 + C e^{-2t})^2} \biggr]^{1/4} \, , </math>

that is,

<math> \Theta_H = \biggl[ \frac{3 C }{(1 + C \xi^2)^2} \biggr]^{1/4} \, . </math>

where <math>C</math> is an integration constant. Because <math>\Theta_H</math> must go to unity when <math>\xi = 0</math>, we see that <math>C=1/3</math>. Hence,

<math> \Theta_H = \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-1/2} \, . </math>

Related Wikipedia Discussions

User:Tohline/SSC/Structure/PolytropesEmbedded

Contents