Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/BinaryFission"
| (One intermediate revision by the same user not shown) | |||
| Line 24: | Line 24: | ||
<font color="green">The ancient problem of whether a rotating, contracting star will, if it has sufficient angular momentum, subdivide and become a binary system must now be reexamined. The existence of generalized zero-viscosity polytropic sequences which do not terminate and which do reach the points of dynamical over stability … answers several of the objections that have been raised against the fission hypothesis. The new situation was reviewed by [https://trove.nla.gov.au/work/21340423?selectedversion=NBD179107 J. P. Ostriker (1970)] in a discussion which anticipates the results presented in this paper. A point of view is presented by [https://ui.adsabs.harvard.edu/abs/1972ApJ...175..171L/abstract N. R. Lebovitz (1972)] which envisions a different evolution but predicts fission at the same critical value of</font> <math>~T/|W|</math>. | <font color="green">The ancient problem of whether a rotating, contracting star will, if it has sufficient angular momentum, subdivide and become a binary system must now be reexamined. The existence of generalized zero-viscosity polytropic sequences which do not terminate and which do reach the points of dynamical over stability … answers several of the objections that have been raised against the fission hypothesis. The new situation was reviewed by [https://trove.nla.gov.au/work/21340423?selectedversion=NBD179107 J. P. Ostriker (1970)] in a discussion which anticipates the results presented in this paper. A point of view is presented by [https://ui.adsabs.harvard.edu/abs/1972ApJ...175..171L/abstract N. R. Lebovitz (1972)] which envisions a different evolution but predicts fission at the same critical value of</font> <math>~T/|W|</math>. | ||
</td></tr></table> | </td></tr></table> | ||
* [https://ui.adsabs.harvard.edu/abs/ | * [https://ui.adsabs.harvard.edu/abs/1984Ap%26SS..99...71H/abstract I. Hachisu & Y. Eriguchi (1984)], Astrophysics & Space Sciences, 99, 71: ''Fission Sequence and Equilibrium Models of Rigidity [sic] Rotating Polytropes'' | ||
* [http://www.phys.lsu.edu/astro/movie_captions/fission.html Webpage summary of Cazes' simulations] | * [http://www.phys.lsu.edu/astro/movie_captions/fission.html Webpage summary of Cazes' simulations] | ||
* [https://inis.iaea.org/search/search.aspx?orig_q=RN:17071096 R. H. Durisen & J. E. Tohline (1985)], ''Protostars and Planets II'', pp. 534 - 575, Univ. of Arizona Press: <font color="maroon"> ''Fission of Rapidly Rotating Fluid Systems''</font> | * [https://inis.iaea.org/search/search.aspx?orig_q=RN:17071096 R. H. Durisen & J. E. Tohline (1985)], ''Protostars and Planets II'', pp. 534 - 575, Univ. of Arizona Press: <font color="maroon"> ''Fission of Rapidly Rotating Fluid Systems''</font> | ||
* [http://articles.adsabs.harvard.edu//full/1986ormo.conf..487D/0000487.000.html Durisen & Gingold (198x)], <font color="maroon">''Numerical Simulations of Fission''</font> | * [http://articles.adsabs.harvard.edu//full/1986ormo.conf..487D/0000487.000.html Durisen & Gingold (198x)], <font color="maroon">''Numerical Simulations of Fission''</font> | ||
* [https://ui.adsabs.harvard.edu/abs/1987GApFD..38...15L/abstract N. R. Lebovitz (1987)], Geophysical and Astrophysical Fluid Dynamics, 38, 15: <font color="maroon">''Binary Fission via Inviscid Trajectories''</font> | |||
<ul> | <ul> | ||
<li>Phase-Transition Theory of Instabilities:</li> | <li>Phase-Transition Theory of Instabilities:</li> | ||
| Line 95: | Line 96: | ||
The nuclear physics community also draws an analogy between the fission of a rotating fluid drop and the spontaneous fission of atomic nuclei; see, for example, the figure associated with the [http://en.wikipedia.org/wiki/Nuclear_fission#Energetics Wikipedia discussion of the energetics of nuclear fission]. | The nuclear physics community also draws an analogy between the fission of a rotating fluid drop and the spontaneous fission of atomic nuclei; see, for example, the figure associated with the [http://en.wikipedia.org/wiki/Nuclear_fission#Energetics Wikipedia discussion of the energetics of nuclear fission]. | ||
See also [https://ui.adsabs.harvard.edu/abs/1967ApJ...148..825R/abstract C. E. Rosenkilde ( | See also [https://ui.adsabs.harvard.edu/abs/1967ApJ...148..825R/abstract C. E. Rosenkilde (1967b)], ApJ, 148, 825: ''The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid''. The first few lines of the Appendix of this paper state … | ||
<table align="center" width="80%"><tr><td align="left"> | <table align="center" width="80%"><tr><td align="left"> | ||
<font color="green"> | <font color="green"> | ||
"The virial method has recently been extended to phenomena of interest in the theory of nuclear fission (Rosenkilde | "The virial method has recently been extended to phenomena of interest in the theory of nuclear fission ([https://ui.adsabs.harvard.edu/abs/1967JMP.....8...98R/abstract Rosenkilde 1967a)]</font>, Journal of Mathematical Physics, 8, 98 <font color="green">… For a rotating, charged, inviscid liquid drop held together by surface tension, there exist axisymmetric figures of equilibrium which are nearly spheroids. Moreover, prolate as well as oblate figures are possible. If these figures are assumed to be spheroids, then the investigation (based on the virial method) of their stability closely resembles the corresponding investigation for the self-gravitating Maclaurin spheroids …" | ||
</font> | </font> | ||
</td></tr></table> | </td></tr></table> | ||
Latest revision as of 20:17, 25 June 2019
Fission Hypothesis of Binary Star Formation
|
"This paper is concerned with one of the oldest hypotheses in stellar-evolution theory, namely, that a binary system originates from the splitting of a single star into two components due to rotational instability during contraction of the star. In spite of many attempts, no satisfactory theory of this process has been developed …" |
|
— Drawn from §I of Ian W. Roxburgh (1966) |

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Potentially Useful References
- S. Chandrasekhar (1965), Proc. Roy. Soc. London. Series A, Mathematical and Physical Sciences, 286, pp. 1 - 26: The Stability of a Rotating Liquid Drop
- I. W. Roxburgh (1966), ApJ, 143, 111: On the Fission Theory of the Origin of Binary Stars
- J. P. Ostriker (1970), Stellar Rotation: Proceedings of the IAU Colloquium held at the Ohio State University, Columbus, OH, U.S.A., September 8-11, 1969, edited by Arne Slettebak, p. 147: Fission and the Origin of Binary Stars
- N. R. Lebovitz (1972), ApJ, 175, 171: On the Fission Theory of Binary Stars
- §IVa of P. Bodenheimer & J. P. Ostriker (1973), ApJ, 180, 159 [Part VIII]
|
The ancient problem of whether a rotating, contracting star will, if it has sufficient angular momentum, subdivide and become a binary system must now be reexamined. The existence of generalized zero-viscosity polytropic sequences which do not terminate and which do reach the points of dynamical over stability … answers several of the objections that have been raised against the fission hypothesis. The new situation was reviewed by J. P. Ostriker (1970) in a discussion which anticipates the results presented in this paper. A point of view is presented by N. R. Lebovitz (1972) which envisions a different evolution but predicts fission at the same critical value of <math>~T/|W|</math>. |
- I. Hachisu & Y. Eriguchi (1984), Astrophysics & Space Sciences, 99, 71: Fission Sequence and Equilibrium Models of Rigidity [sic] Rotating Polytropes
- Webpage summary of Cazes' simulations
- R. H. Durisen & J. E. Tohline (1985), Protostars and Planets II, pp. 534 - 575, Univ. of Arizona Press: Fission of Rapidly Rotating Fluid Systems
- Durisen & Gingold (198x), Numerical Simulations of Fission
- N. R. Lebovitz (1987), Geophysical and Astrophysical Fluid Dynamics, 38, 15: Binary Fission via Inviscid Trajectories
- Phase-Transition Theory of Instabilities:
- D. M. Christodoulou, D. Kazanas, I. Shlosman & J. E. Tohline (1995a), ApJ, 446, 472: Second-Harmonic Instability and Bifurcation Points
- D. M. Christodoulou, D. Kazanas, I. Shlosman & J. E. Tohline (1995b), ApJ, 446, 485: Fourth-Harmonic Bifurcations and λ-Transitions
- D. M. Christodoulou, D. Kazanas, I. Shlosman & J. E. Tohline (1995c), ApJ, 446, 500: The Third-Harmonic Bifurcation on the Jacobi Sequence and the Fission Problem
- D. M. Christodoulou, D. Kazanas, I. Shlosman & J. E. Tohline (1995d), ApJ, 446, 510: Critical Points on the Maclaurin Sequence and Nonlinear Fission Processes
- I. A. Bonnell (2001), Proceedings of IAU Symposium 200, held 10 - 15 April, 2000 in Potsdam, Germany, edited by Hans Zinnecker and Robert D. Mathieu, p. 23: The Formation of Close Binary Stars
- J. T. Tohline (2002), ARAA, 40, 349: The Origin of Binary Stars
Illustration
|
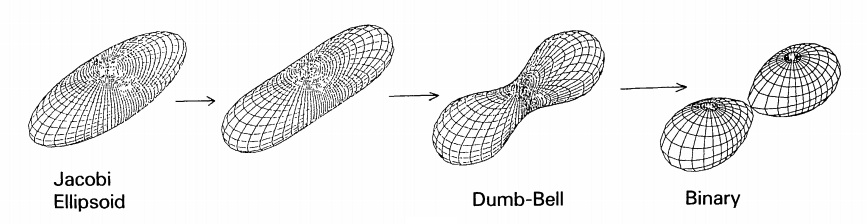
Figure 1
|
Figure 2
|
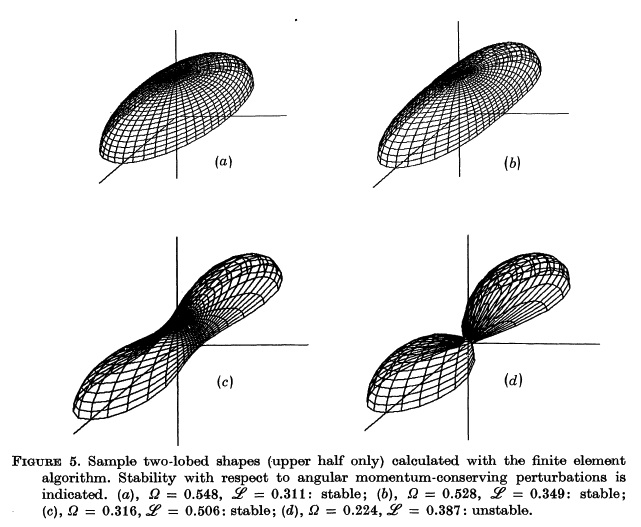
Figure 4
|
|
|
Figure 3
|
Figure 5
|
||
Related Discussions
Fission in Nuclear Physics
The nuclear physics community also draws an analogy between the fission of a rotating fluid drop and the spontaneous fission of atomic nuclei; see, for example, the figure associated with the Wikipedia discussion of the energetics of nuclear fission.
See also C. E. Rosenkilde (1967b), ApJ, 148, 825: The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid. The first few lines of the Appendix of this paper state …
|
"The virial method has recently been extended to phenomena of interest in the theory of nuclear fission (Rosenkilde 1967a), Journal of Mathematical Physics, 8, 98 … For a rotating, charged, inviscid liquid drop held together by surface tension, there exist axisymmetric figures of equilibrium which are nearly spheroids. Moreover, prolate as well as oblate figures are possible. If these figures are assumed to be spheroids, then the investigation (based on the virial method) of their stability closely resembles the corresponding investigation for the self-gravitating Maclaurin spheroids …" |
Drop Dynamics Experiments
[On 1 January 2014, J. E. Tohline wrote ...] As I was putting this chapter together, I had difficulty documenting the various drop dynamics experiments that have been conducted by astronauts in various Earth-orbiting (zero <math>g</math>) environments. Here is the relevant information that I have found, to date.
Skylab
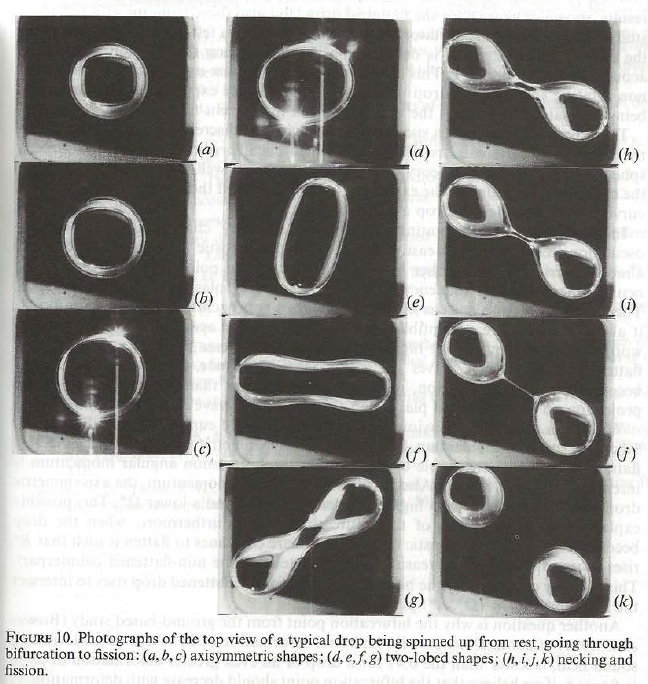
Experiments showing the fission of liquid drops were evidently conducted during the Skylab 2, Skylab 3, and Skylab 4 missions (circa 1973-1974).
- As has been documented in a short film review written by Howard Voss and published in the American Journal of Physics (44/10, 1021, Oct 1976), film footage from a variety of Skylab experiments was produced by NASA, edited by Thomas Campbell & Robert Fuller, and, beginning in 1976, distributed as 12 Super 8 film loops by the American Association of Physics Teachers (AAPT).
- As is documented in A Teacher's Guide for the Skylab Physics Videodisc the content of all 12 Super 8 film loops was made available for distribution in Videodisc format in 1987 through the AAPT.
- The YouTube video referenced in and linked to the caption of Figure 1, above, is the digitized version of the Skylab film loop that illustrates fission of a water droplet.
|
According to the Teacher's Guide mentioned above, the activities shown in the above-referenced films were carried out by three teams of Skylab Astronauts: |
|
|
|
|
Space Shuttle Flights
Experiments illustrating the dynamical behavior of liquid drops were conducted during several space shuttle missions. Some experiments were performed inside the European Space Agency's "spacelab module" and others were performed with the aid of a "Drop Physics Module (DPM)" inside the United States Microgravity Laboratory (USML), each being a "portable" laboratory that was housed in the shuttle's payload bay.
- Wang, Trinh, Croonquist, and Elleman (1986; Physical Review Letters, 56, 452) report results from a controlled drop dynamics experiment that was conducted during the "Spacelab III mission" (see the final acknowledgement paragraph of their paper), which took place during shuttle flight STS-51-B (29 April - 6 May 1985). Taylor Wang — one of the authors of this PRL publication — flew as one of the seven members of the space shuttle crew, specifically as Payload Specialist 2. His narrated account of some of the experimental activities is available, beginning at 7 minutes 32 seconds into the STS-51B "Post Flight Presentation" video.
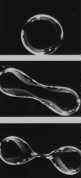
- Another mission — USML-1 during shuttle flight STS-50 — took place in early 1992. According to information provided by NASA/JPL's public information office, "… the transition of rotating liquid drops into a 'dog-bone,' or two-lobed shape, was studied in detail …" As can be seen, beginning at 2 minutes 28 seconds into the STS-50 "Post Flight Presentation" video, Eugene Trinh flew was one of the members of this shuttle mission who conducted these DMP experiments. Detailed results from DPM experiments during the USML-1 mission have been published in the Journal of Fluid Mechanics: T. G. Wang, A. V. Anilkumar, C. P. Lee and K. C. Lin (1994). Bifurcation of rotating liquid drops: results from USML-1 experiments in Space. Journal of Fluid Mechanics, 276, pp 389-403
- I think that the three-frame black & white image shown here on the right presents a result from mission USML-1. That is how this image is referenced in an online discussion of fission that I put together about a decade ago.
- Yet another mission — USML-2 during shuttle flight STS-73 — took place in the fall of 1995. Some additional drop dynamics experiments were conducted during this mission — see, for example, about 7 minutes and 40 seconds into the STS-73 "Post Flight Presentation" video. Lee, Anilkumar, Hmelo, & Wang (1998; Journal of Fluid Mechanics, 354, 43) report results from these controlled drop dynamics experiments.
International Space Station
- See the two "Gallery of Fluid Motions" mpg movies that accompany the preprint by Ueno et al. (2012).
Online References
- The Fission Mechanism for Binary Star Formation
- Fission Simulations at LSU
- T. G. Wang, A. V. Anilkumar, C. P. Lee and K. C. Lin (1994). Bifurcation of rotating liquid drops: results from USML-1 experiments in Space. Journal of Fluid Mechanics, 276, pp 389-403
- Ohsaka & Trinh (19xx)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |