Virial Stability of BiPolytropes

BiPolytrope

[Following a discussion that Tohline had with Kundan Kadam on 3 July 2013, we have decided to carry out a virial equilibrium and stability analysis of nonrotating bipolytropes.]

We will adopt the following approach:

Properties of the core <math>\cdots</math>
- Uniform density, <math>\rho_c</math>;
- Polytropic constant, <math>K_c</math>, and polytropic index, <math>n_c</math>;
- Surface of the core at <math>r_i</math>;
Properties of the envelope <math>\cdots</math>
- Uniform density, <math>\rho_e</math>;
- Polytropic constant, <math>K_e</math>, and polytropic index, <math>n_e</math>;
- Base of the core at <math>r_i</math> and surface at <math>R</math>.

Use the dimensionless radius,

<math>\xi \equiv \frac{r}{r_i}</math>.

Then, <math>\xi_i = 1</math> and <math>\xi_s \equiv R/r_i</math>.

Expressions for Mass

Inside the core, the expression for the mass interior to any radius, <math>0 \le \xi \le 1</math>, is,

<math>M_\xi = \frac{4\pi}{3} \rho_c r_i^3 \xi^3</math> .

The expression for the mass interior to any position within the envelope, <math>1 \le \xi \le \xi_s</math>, is,

<math>M_\xi = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi^3 - 1) \biggr]</math> .

Hence, the mass of the core, the mass of the envelope, and the total mass are, respectively,

<math>M_\mathrm{core} = \frac{4\pi}{3} \rho_c r_i^3 = M_0 \biggl[ \frac{\rho_c}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math> <math>\Rightarrow</math> <math>\frac{\rho_c}{\rho_0} = \frac{M_\mathrm{core}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3}</math> ;

<math>M_\mathrm{env} = \frac{4\pi}{3} r_i^3 \biggl[\rho_e (\xi_s^3 - 1) \biggr] = M_0 (\xi_s^3 - 1) \biggl[ \frac{\rho_e}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr]</math> <math>\Rightarrow</math> <math>\frac{\rho_e}{\rho_0} = \frac{M_\mathrm{env}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3} (\xi_s^3 - 1)^{-1}</math> ;

<math>M_\mathrm{tot} = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi_s^3 - 1) \biggr] = M_0 \biggl( \frac{\rho_c}{\rho_0} \biggr) \biggl( \frac{r_i}{R_0}\biggr)^3 \biggl[ 1 + \frac{\rho_e}{\rho_c} (\xi_s^3 - 1) \biggr] </math> ;

where, <math>M_0 \equiv 4\pi \rho_0 R_0^3/3</math>. Letting <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> — which also means, <math>M_\mathrm{env}/M_\mathrm{tot} = (1-\nu) </math> — we can write,

<math>\frac{\rho_e}{\rho_c} = \frac{M_\mathrm{env}}{M_\mathrm{core}} (\xi_s^3 - 1)^{-1} = \frac{(1-\nu)}{\nu (\xi_s^3 - 1)} </math> ,

and,

<math>\nu (\xi_s^3 - 1) \biggl( \frac{\rho_e}{\rho_c} \biggr) = (1-\nu) </math> <math>\Rightarrow</math> <math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1}</math> .

Following the work of Schönberg & Chandrasekhar (1942) — see our accompanying discussion — we are seeking equilibrium configurations in the <math>\nu - q</math> plane where,

<math>\nu</math>	<math>\equiv</math>	<math>\frac{M_\mathrm{core}}{M_\mathrm{tot}} </math>, (as also defined here)
<math>q</math>	<math>\equiv</math>	<math>\frac{r_i}{R} = \frac{1}{\xi_s}</math> .

So we can rewrite the above expression as,

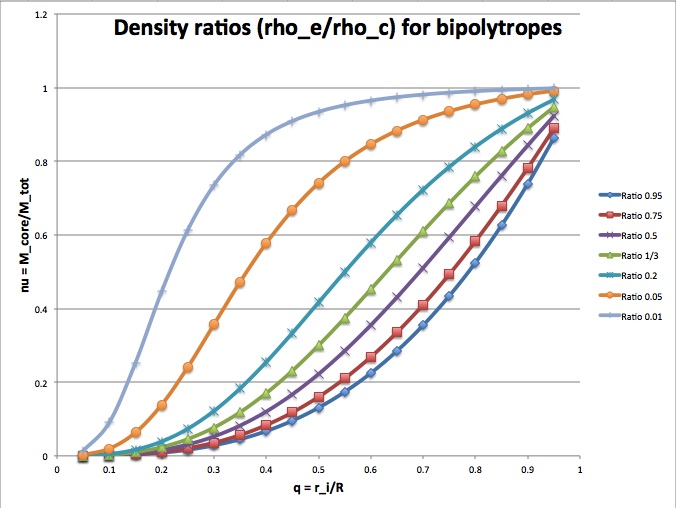
<math>\nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^3} - 1\biggr) \biggr]^{-1}</math> .

The following figure shows how <math>\nu</math> varies with <math>q</math> for various choices of the mass density ratio, <math>\rho_e/\rho_c</math>. It illustrates that, for a given core-to-total mass ratio, <math>\nu</math>, the relative location of the interface radius, <math>q</math>, can vary between zero and one, but each value of <math>q</math> reflects a different ratio of envelope-to-core mass density.

Energy Expressions

The gravitational potential energy of the bipolytropic configuration is obtained by integrating over the following differential energy contribution,

<math>dW = - \biggl( \frac{GM_r}{r} \biggr) dm</math> .

Hence,

<math>W = W_\mathrm{core} + W_\mathrm{env}</math>	<math> = - G \biggl\{ \int_0^{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_c dr + \int^R_{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_e dr \biggr\} </math>
	<math> = - G \biggl\{ \int_0^1 \biggl( \frac{4\pi }{3} \rho_c r_i^3 \xi^3 \biggr) 4\pi r_i^2 \rho_c \xi d\xi + \int_1^{\xi_s} \frac{4\pi}{3} \rho_c r_i^3 \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] 4\pi r_i^2 \rho_e \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \int_0^1 \xi^4 d\xi + \int_1^{\xi_s} \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] \biggl( \frac{\rho_e}{\rho_c} \biggr) \xi d\xi \biggr\} </math>
	<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \frac{1}{5} + \biggl( \frac{\rho_e}{\rho_c} \biggr) \int_1^{\xi_s} \xi d\xi + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \int_1^{\xi_s} (\xi^3 - 1) \xi d\xi \biggr\} </math>
	<math> = - \biggl( \frac{GM^2_\mathrm{tot}}{R} \biggr) 3\nu^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math>

I like the form of this expression. The leading term, which scales as <math>R^{-1}</math>, encapsulates the behavior of the gravitational potential energy for a given choice of the internal structure, namely, a given choice of <math>\xi_s</math>, <math>\nu</math>, and density ratio <math>(\rho_e/\rho_c)</math>. Actually, only two internal structural parameters need to be specified — <math>\xi_s</math> and <math>f_c</math>; from these two, the expressions shown above allow the determination of both <math>(\rho_e/\rho_c)</math> and <math>\nu</math>.

The internal energy of the bipolytropic configuration is,

<math> U = U_\mathrm{core} + U_\mathrm{env} </math>	<math>= \frac{2}{3}\biggl\{ \frac{S_\mathrm{core}}{(\gamma_c-1)} + \frac{S_\mathrm{env}}{(\gamma_e-1)} \biggr\} </math>
	<math>= \biggl\{ n_c M_\mathrm{core} K_c \rho_c^{1/n_c} + n_e M_\mathrm{env} K_e \rho_e^{1/n_e} \biggr\} \, . </math>
	<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \rho_c^{1/n_c} + n_e (1-\nu) K_e \rho_e^{1/n_e} \biggr\} \, . </math>
	<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{1/n_e} \biggr\} \, . </math>

Now, try to write this in such a way that the pressure in the envelope equals the pressure in the core (uniform pressure configuration) even as the overall radius of the configuration is varied in order to search for the equilibrium configuration. That is, set

<math>K_c \rho_c^{1+1/n_c} </math>	=	<math>K_e \rho_e^{1+1/n_e}</math>
<math>\Rightarrow ~~~~~~~~ \frac{K_e}{K_c}</math>	=	<math>\frac{\rho_c^{1+1/n_c}}{\rho_e^{1+1/n_e}}</math>
	=	<math>\biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1+1/n_c} \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{-1-1/n_e} \, .</math>

Hence, the expression for the internal energy becomes,

<math> U </math>	<math>= K_c M_\mathrm{tot} \biggl\{ n_c \nu \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1+1/n_c} \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{-1} \biggr\} \, . </math>
	<math>= K_c M_\mathrm{tot} \nu \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} \biggl\{ n_c + n_e (\xi_s^3-1) \biggr\} </math>
	<math>= K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{1/n_c} R^{-3/n_c} [ n_c + n_e (\xi_s^3-1) ] \nu^{1+1/n_c} \xi_s^{3/n_c} </math>

Virial Analysis

Employing the above derived expressions, the free energy may be written as,

<math> \mathfrak{G} = W + U = - A\biggl( \frac{R}{R_0} \biggr)^{-1} + B \biggl( \frac{R}{R_0} \biggr)^{-3/n_c} \, , </math>

where, <math>R_0</math> is a, as yet unspecified, scale length, and,

<math> A </math>	<math>=</math>	<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math>
<math>B</math>	<math>=</math>	<math> n_cK_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} \, . </math>
	<math>=</math>	<math> n_c M_\mathrm{tot} \bar{c_s}^2 \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} \, . </math>

These should be used in conjunction with the relations derived above, namely,

<math> \biggl( \frac{\rho_e}{\rho_c} \biggr) </math>

<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, , </math>

and,

<math> \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1} \, , </math>

where, we recall,

<math>f_c \equiv \frac{\rho_c}{\rho_c|_0}</math> and <math>\xi_s \equiv \frac{R}{r_i}</math> .

Scenarios

Generally, we will define a bipolytropic configuration by specifying:

The polytropic index of the core, <math>n_c</math>, and the envelope <math>n_e</math> ;
The total mass, <math>M_\mathrm{tot}</math> ;
The specific entropy of the core material, via the specification of the polytropic constant of the core, <math>K_c</math> .

Next, we will choose:

The fractional radius of the core, <math>r_i/R = 1/\xi_s</math> ;
The initial ratio of density in the envelope to density in the core, <math>(\rho_e/\rho_c)_0</math> ; also set <math>f_c = 1</math>, indicating that <math>(\rho_e/\rho_c) = (\rho_e/\rho_c)_0</math>.

With these values in hand, we can determine:

The ratio of the core mass to total mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> ;
The free-energy coefficients, <math>A</math> and <math>B</math> ;

and the free energy <math>\mathfrak{G}</math> can be evaluated for a wide variety of choices of configuration radii, <math>R</math>.

We retrieve the expression for the single polytrope by setting <math>n_e = n_c</math> and <math>(\rho_e/\rho_c)_0 = 1</math>, for any choice of <math>\xi_s</math>.

Equilibria

The radii of equilibrium configurations, <math>R_\mathrm{eq}</math>, are identified by the condition,

<math>\frac{\partial \mathfrak{G}}{\partial R} = 0 \, .</math>

As in the case of the single polytrope, this condition is satisfied if we set <math>R_0 = R_\mathrm{eq}</math> and,

This implies,

<math> \frac{5\bar{c_s}^2 R_\mathrm{eq}}{GM_\mathrm{tot}} </math>

<math> \nu^{-1/n_c} \xi_s^{2-3/n_c} \biggl\{ 1 + \frac{5}{2} \biggl(\frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl(\frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2 - 1) \biggr] \biggr\} \biggl[ 1 + \frac{n_e}{n_c}( \xi_s^3 - 1 ) \biggr]^{-1} \, , </math>

where,

<math> \frac{\rho_e}{\rho_c} = \biggl(\frac{1}{\nu} - 1 \biggr) (\xi_s^3 - 1)^{-1} \, , </math>

and

Finally, the value of the free energy in each equilibrium configuration is,

<math> \mathfrak{G}\biggr\|_{R_\mathrm{eq}} </math>	<math> = </math>	<math> B - A </math>
	<math> = </math>	<math> n_c M_\mathrm{tot} \bar{c_s}^2 \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - \biggl( \frac{3GM^2_\mathrm{tot}}{5R_\mathrm{eq}} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math>
<math> \biggl( M_\mathrm{tot} \bar{c_s}^2 \biggr)^{-1} \mathfrak{G}\biggr\|_{R_\mathrm{eq}} </math>	<math> = </math>	<math> n_c \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - \biggl( \frac{3GM_\mathrm{tot}}{5\bar{c_s}^2 R_\mathrm{eq}} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} </math>
	<math> = </math>	<math> n_c \biggl\{ \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \nu^{1+1/n_c} \xi_s^{3/n_c} \biggr\} - 3 \nu^2 \xi_s \biggl[ 1 + \frac{n_e}{n_c}( \xi_s^3 - 1 ) \biggr] \nu^{1/n_c} \xi_s^{3/n_c-2} </math>
	<math> = </math>	<math> n_c \nu^{1 + 1/n_c} \xi_s^{3/n_c} \biggl[ 1 + \frac{n_e}{n_c} (\xi_s^3-1) \biggr] \biggl\{ 1 - \frac{3 \nu}{n_c \xi_s} \biggr\} </math>

Virial Analysis (2nd Try)

Let's go back to a more general expression for the internal energy, namely,

<math> U = U_\mathrm{core} + U_\mathrm{env} </math>	<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \nu r_i^{-3} \biggr]^{1/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) (1-\nu)(\xi_s^3-1)^{-1} r_i^{-3} \biggr]^{1/n_e} \biggr\} </math>
	<math>= M_\mathrm{tot} \biggl\{ n_c \nu K_c \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr) \nu \xi_s^{3} \biggr]^{1/n_c} \biggl(\frac{R}{R_0}\biggr)^{-3/n_c} + n_e (1-\nu) K_e \biggl[ \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr) (1-\nu)(\xi_s^3-1)^{-1} \xi_s^{3} \biggr]^{1/n_e} \biggl(\frac{R}{R_0}\biggr)^{-3/n_e} \biggr\} \, . </math>

Ultimately, we will relate <math>K_e</math> to <math>K_c</math> by demanding that initially the pressure is identical in both layers. As derived earlier, this will be accomplished via the expression,

=

<math>\biggl[ \frac{\rho_c^{1+1/n_c}}{\rho_e^{1+1/n_e}} \biggr]_0 \, .</math>

The free energy may now be written as,

<math> \mathfrak{G} = W + U = - A\biggl( \frac{R}{R_0} \biggr)^{-1} + B_c \biggl( \frac{R}{R_0} \biggr)^{-3/n_c} + B_e \biggl( \frac{R}{R_0} \biggr)^{-3/n_e} \, , </math>

where, <math>R_0</math> is a, as yet unspecified, scale length, and,

<math> A </math>	<math>=</math>	<math> \biggl( \frac{3GM^2_\mathrm{tot}}{5R_0} \biggr) \nu^2 \xi_s \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (\xi_s^5 - 1) - \frac{5}{2}(\xi_s^2-1) \biggr] \biggr\} \, , </math>
<math>B_c</math>	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} \, , </math>
<math>B_e</math>	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} \, . </math>

These should be used in conjunction with the relations derived above, namely,

<math> \biggl( \frac{\rho_e}{\rho_c} \biggr) </math>

<math> \frac{1}{f_c} \biggl\{ \biggl( \frac{\rho_e} {\rho_c}\biggr)_0 + \biggl[ \frac{( 1 - f_c )}{ (\xi_s^3 - 1) } \biggr] \biggr\} \, , </math>

and,

<math> \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^3 - 1) \biggr]^{-1} \, , </math>

where, we recall,

<math>f_c \equiv \frac{\rho_c}{\rho_c|_0}</math> and <math>\xi_s \equiv \frac{R}{r_i}</math> .

Equilibria

Now let's evaluate the variation of the free energy with <math>R</math>.

<math> R_0 \cdot \frac{\partial \mathfrak{G}}{\partial R}\biggr|_{A, B_c, B_e} = A \biggl(\frac{R}{R_0}\biggr)^{-2} - \frac{3B_c}{n_c} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_c} - \frac{3B_e}{n_e} \biggl(\frac{R}{R_0}\biggr)^{-1-3/n_e} \, . </math>

Equilibria are defined by setting this first-derivative of <math>\mathfrak{G}</math> to zero. So, letting <math>R_0 \equiv R_\mathrm{equil}</math>, we see that the configuration is in equilibrium when <math>R = R_0</math>, which means,

Now let's evaluate the second derivative at the equilibrium radius where <math>R = R_0</math>:

<math> R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr\|_{A, B_c, B_e} </math>	<math>=</math>	<math> -2 A \biggl(\frac{R}{R_0}\biggr)^{-3} + \frac{3B_c}{n_c} \biggl( 1+\frac{3}{n_c} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_c} + \frac{3B_e}{n_e} \biggl( 1+\frac{3}{n_e} \biggr) \biggl(\frac{R}{R_0}\biggr)^{-2-3/n_e} </math>
<math> n_c n_e R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr\|_{A, B_c, B_e} </math>	<math>=</math>	<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 2n_c n_e A </math>
	<math>=</math>	<math> 3n_e B_c \biggl( 1+\frac{3}{n_c} \biggr) + 3n_c B_e \biggl( 1+\frac{3}{n_e} \biggr) - 6(n_e B_c + n_c B_e) </math>
<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr\|_{A, B_c, B_e} </math>	<math>=</math>	<math> 3n_e^2 B_c (3 -n_c ) + 3n_c^2 B_e ( 3 - n_e) \, . </math>

Let's relate <math>B_e</math> to <math>B_c</math>.

<math>B_c</math>	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} </math>
	<math>=</math>	<math> n_c K_c M_\mathrm{tot} \biggl[ \frac{\rho_c\|_0 }{\nu \xi_s^3} \biggr]^{1/n_c} \nu^{1+1/n_c} \xi_s^{3/n_c} = n_c K_c M_\mathrm{tot} \biggl[ \rho_c\|_0 \biggr]^{1/n_c} \nu = \biggl[ \frac{n_c \nu M_\mathrm{tot}}{\rho_c\|_0} \biggr] K_c \biggl( \rho_c \biggr)_0^{1+1/n_c} </math>
<math>B_e</math>	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_0^3} \biggr)^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} </math>
	<math>=</math>	<math> n_e K_e M_\mathrm{tot} \biggl[ \frac{(\xi_s^3 - 1) \rho_e\|_0 }{(1-\nu) \xi_s^3} \biggr]^{1/n_e} (1 - \nu)^{1+1/n_e} \xi_s^{3/n_e} (\xi_s^3 - 1)^{-1/n_e} = n_e K_e M_\mathrm{tot} \biggl[ \rho_e\|_0 \biggr]^{1/n_e} (1 - \nu) </math>
	<math>=</math>	<math> \biggl[ \frac{n_e (1 - \nu) M_\mathrm{tot}}{\rho_e\|_0} \biggr] K_e \biggl( \rho_e \biggr)_0^{1+1/n_e} </math>
<math>\Rightarrow ~~~~ B_e</math>	<math>=</math>	<math> B_c \biggl[ \frac{n_e (1 - \nu) }{n_c \nu } \biggr] \biggl( \frac{\rho_e}{\rho_c}\biggr)_0^{-1} = B_c \biggl( \frac{n_e}{n_c} \biggr) (\xi_s^3 -1) \, . </math>

Hence,

<math> (n_c n_e)^2 R_0^2 \cdot \frac{\partial^2 \mathfrak{G}}{\partial R^2}\biggr|_{A, B_c, B_e} </math>

<math> 3n_eB_c \biggl\{ n_e (3 -n_c ) + n_c ( 3 - n_e)(\xi_s^3 -1) \biggr\} \, . </math>

This second derivative becomes negative and, hence, the configuration becomes unstable, when,

that is, when,

<math> q \equiv \frac{1}{\xi_s} > \biggl[ 1 + \frac{n_e(n_c-3)}{n_c(3-n_e)} \biggr]^{-1/3} \, . </math>

Some example values of <math>q_\mathrm{crit}</math> are provided in the following table.

Table 1: Values of <math>q_\mathrm{crit}</math> and <math>\nu_\mathrm{crit}</math> for various bipolytropes
<math>n_c</math>	<math>n_e</math>	<math>\xi_\mathrm{crit}^3</math>	<math>q_\mathrm{crit}</math>	<math>\nu_\mathrm{crit}</math>
<math>n_c</math>	<math>n_e</math>	<math>\xi_\mathrm{crit}^3</math>	<math>q_\mathrm{crit}</math>	<math>\frac{\rho_e}{\rho_c} = 1</math>	<math>\frac{\rho_e}{\rho_c} = \frac{1}{2}</math>
<math>5</math>	<math>1</math>	<math>\frac{6}{5}</math>	<math>0.941</math>	<math>\frac{5}{6}</math>	<math>\frac{10}{11}</math>
<math>5</math>	<math>\frac{3}{2}</math>	<math>\frac{7}{5}</math>	<math>0.894</math>	<math>\frac{5}{7}</math>	<math>\frac{10}{12}</math>
<math>\gg 3</math>	<math>\frac{3}{2}</math>	<math>2</math>	<math>0.794</math>	<math>\frac{1}{2}</math>	<math>\frac{2}{3}</math>

The associated critical value of the mass ratio, <math>\nu_\mathrm{crit}</math>, depends on the selection of the chosen density ratio via the relation,

<math> \nu_\mathrm{crit} = \biggl[1 + \biggl(\frac{\rho_e}{\rho_c}\biggr)(\xi_\mathrm{crit}^3 - 1) \biggr]^{-1} \, . </math>

Virial Analysis (3rd Try)

As in the <math>2^\mathrm{nd}</math> try, above, the free energy may be written as,

<math> \mathfrak{G} = W + U = - A \chi^{-1} + B_c \chi^{-3/n_c} + B_e \chi^{-3/n_e} \, , </math>

where, <math>\chi \equiv R/R_0</math>.

<math> \frac{\partial\mathfrak{G}}{\partial \chi} = A \chi^{-2} -\frac{3}{n_c} B_c \chi^{-(1+3/n_c)} -\frac{3}{n_e} B_e \chi^{-(1+3/n_e)} \, ; </math>

<math> \frac{\partial^2\mathfrak{G}}{\partial \chi^2} = -2 A \chi^{-3} + \frac{3}{n_c} \biggl(1+\frac{3}{n_c}\biggr) B_c \chi^{-(2+3/n_c)} + \frac{3}{n_e} \biggl(1+\frac{3}{n_e}\biggr) B_e \chi^{-(2+3/n_e)} \, . </math>

We obtain the equilibrium radius, <math>\chi_E</math>, when <math>\partial\mathfrak{G}/\partial\chi = 0</math>. Hence, the relation governing the equilibrium radius is,

<math> A \chi_E^{-2} </math>	<math>=</math>	<math> \frac{3}{n_c} B_c \chi_E^{-(1+3/n_c)} +\frac{3}{n_e} B_e \chi_e^{-(1+3/n_e)} </math>
<math> \Rightarrow ~~~~~ \alpha </math>	<math>=</math>	<math> \chi_E^{1-3/n_c} +\beta \chi_E^{1-3/n_e} </math>

where,

<math>\alpha \equiv \frac{n_c A}{3B_c} \, ;</math>

<math>\beta \equiv \frac{n_c B_e}{n_e B_c} \, .</math>

Note that for the isothermal case (<math>n_c = \infty</math> in the above exponents),

<math>\alpha \equiv \frac{A}{B_c} \, ;</math>

<math>\beta \equiv \frac{3 B_e}{n_e B_c} \, .</math>

And at this equilibrium radius, the second derivative of the free energy has the value,

<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr|_E </math>

<math> -2 \alpha + \biggl(1+\frac{3}{n_c}\biggr) \chi_E^{1-3/n_c} + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} \, , </math>

which, when combined with the condition for equilibrium gives,

<math> \chi_E^3 \biggl( \frac{n_c}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr\|_E </math>	<math> = </math>	<math> -2 \alpha + \biggl(1+\frac{3}{n_e}\biggr) \beta \chi_E^{1-3/n_e} + \biggl(1+\frac{3}{n_c}\biggr) \biggl[ \alpha - \beta \chi_E^{1-3/n_e} \biggr] </math>
	<math> = </math>	<math> \biggl(\frac{3}{n_c} - 1\biggr) \alpha + 3\beta \biggl(\frac{1}{n_e} - \frac{1}{n_c}\biggr) \chi_E^{1-3/n_e} </math>
<math> \Rightarrow ~~~~~ \chi_E^3 \biggl( \frac{n_e n_c^2}{3B_c} \biggr) \frac{\partial^2\mathfrak{G}}{\partial \chi^2} \biggr\|_E </math>	<math> = </math>	<math> n_e (3- n_c) \alpha + 3\beta (n_c - n_e) \chi_E^{1-3/n_e} </math>

Finally, the equilibrium configuration is stable as long as this second derivative is positive, that is, for,

Isothermal Core

If the core is isothermal, we set <math>n_c = \infty</math>, in which case stability occurs for,

Envelope with <math>n=3/2</math>

If we choose an <math>n_e = 3/2</math> envelope, we obtain stability for,

In this case, the equilibrium radius condition is,

<math> \chi_E^2 - \alpha \chi_E + \beta =0 </math>

<math> \Rightarrow ~~~~ \chi_E = \frac{1}{2}\biggl[\alpha \pm \biggl( \alpha^2 -4\beta \biggr)^{1/2} \biggr] = \frac{\alpha}{2}\biggl[1 \pm \biggl( 1 -\frac{4\beta}{\alpha^2} \biggr)^{1/2} \biggr] </math>

Envelope with <math>n=1</math>

If, instead, we choose an <math>n_e = 1</math> envelope, we obtain stability for,

In this case, the equilibrium radius condition is,

<math> \alpha = \chi_E + \beta \chi_E^{-2} \, , </math>

<math> \Rightarrow ~~~~ \chi_E^3 - \alpha \chi_E^2 + \beta = 0 \, . </math>

User:Tohline/SSC/VirialStability

Contents

Virial Stability of BiPolytropes

BiPolytrope

Expressions for Mass

Energy Expressions

Virial Analysis

Scenarios

Equilibria

Virial Analysis (2nd Try)

Equilibria

Virial Analysis (3rd Try)

Isothermal Core

Envelope with <math>n=3/2</math>

Envelope with <math>n=1</math>

Navigation menu

Search