Difference between revisions of "User:Tohline/SSC/Structure/IsothermalSphere"
(→Isothermal Sphere (structure): Add summary section, patterned after n = 1 polytrope discussion) |
(→Summary: Flesh out summary) |
||
| Line 187: | Line 187: | ||
</div> | </div> | ||
* <font color="red">Density</font>: | * <font color="red">Density & Pressure</font>: | ||
: As a function of the radial coordinate, <math>r(\mathfrak{r}_1)</math>, the density profile is, | : As a function of the radial coordinate, <math>r(\mathfrak{r}_1)</math>, the density profile is, | ||
<div align="center"> | <div align="center"> | ||
<math>\rho(r(\mathfrak{r}_1))= \rho_c v_1(\mathfrak{r}_1)</math> . | <math>\rho(r(\mathfrak{r}_1))= \rho_c v_1(\mathfrak{r}_1)</math>; | ||
</div> | |||
: and the pressure profile is, | |||
<div align="center"> | |||
<math>P(r(\mathfrak{r}_1))= (c_s^2 \rho_c) v_1(\mathfrak{r}_1)</math>. | |||
</div> | </div> | ||
| Line 198: | Line 202: | ||
<math>M_0 \equiv \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} </math> ; | <math>M_0 \equiv \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} </math> ; | ||
</div> | </div> | ||
: and, expressed in terms of <math>M_0</math>, the mass that lies interior to radius <math>r</math> is, | |||
: and, expressed | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
M_r = M_0 | M_r = M_0 [ - \mathfrak{r}_1^2 v_1' ] \, . | ||
</math> | </math> | ||
</div> | </div> | ||
* <font color="red"> | * <font color="red">Enthalpy & Gravitational Potential</font>: | ||
: To within an additive constant, the enthalpy distribution is, | |||
: | |||
<div align="center"> | <div align="center"> | ||
<math>\ | <math>H(r(\mathfrak{r}_1))= c_s^2 \ln[v_1(\mathfrak{r}_1)]</math>; | ||
</div> | </div> | ||
: | : and the gravitational potential is, | ||
<div align="center"> | <div align="center"> | ||
<math>\Phi(r) = - \ | <math>\Phi(r(\mathfrak{r}_1)) = - H(r(\mathfrak{r}_1))= - c_s^2 \ln[v_1(\mathfrak{r}_1)]</math>. | ||
</div> | </div> | ||
* <font color="red">Mass-Radius relationship</font>: | * <font color="red">Mass-Radius relationship</font>: | ||
: We see that, for a given value of <math>\rho_c</math>, the relationship between the configuration's total mass and radius is, | : STILL TO BE WRITTEN! We see that, for a given value of <math>\rho_c</math>, the relationship between the configuration's total mass and radius is, | ||
<div align="center"> | <div align="center"> | ||
<math>M \propto R^3 ~~~~~\mathrm{or}~~~~~R \propto M^{1/3} </math> . | <math>M \propto R^3 ~~~~~\mathrm{or}~~~~~R \propto M^{1/3} </math> . | ||
| Line 244: | Line 226: | ||
* <font color="red">Central- to Mean-Density Ratio</font>: | * <font color="red">Central- to Mean-Density Ratio</font>: | ||
: The ratio of the configuration's central density to its mean density is, | : STILL TO BE WRITTEN! The ratio of the configuration's central density to its mean density is, | ||
<div align="center"> | <div align="center"> | ||
<math>\frac{\rho_c}{\bar{\rho}} = \biggl(\frac{\pi M}{4 R^3} \biggr)\biggl(\frac{3 M}{4 \pi R^3} \biggr) = \frac{\pi^2}{3} </math> . | <math>\frac{\rho_c}{\bar{\rho}} = \biggl(\frac{\pi M}{4 R^3} \biggr)\biggl(\frac{3 M}{4 \pi R^3} \biggr) = \frac{\pi^2}{3} </math> . | ||
Revision as of 16:59, 1 November 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal Sphere (structure)
Here we supplement the simplified set of principal governing equations with an isothermal equation of state, that is, <math>~P</math> is related to <math>~\rho</math> through the relation,
<math>P = c_s^2 \rho \, ,</math>
where, <math>c_s</math> is the isothermal sound speed. Comparing this <math>~P</math>-<math>~\rho</math> relationship to
Form A
of the Ideal Gas Equation of State,
|
<math>~P_\mathrm{gas} = \frac{\Re}{\bar{\mu}} \rho T</math> |
we see that,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} = \frac{k T}{m_u \bar{\mu}} \, ,</math>
where, <math>~\Re</math>, <math>~k</math>, <math>~m_u</math>, and <math>~\bar{\mu}</math> are all defined in the accompanying variables appendix. It will be useful to note that, for an isothermal gas, <math>~H</math> is related to <math>~\rho</math> via the expression,
<math> dH = \frac{dP}{\rho} = c_s^2 d\ln\rho \, . </math>
Governing Relations
Adopting solution technique #2, we need to solve the following second-order ODE relating the two unknown functions, <math>~\rho</math> and <math>~H</math>:
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{dH}{dr} \biggr) =- 4\pi G \rho</math> .
Using the <math>~H</math>-<math>~\rho</math> relationship for an isothermal gas presented above, this can be rewritten entirely in terms of the density as,
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\ln\rho}{dr} \biggr) =- \frac{4\pi G}{c_s^2} \rho \, ,</math>
or, equivalently,
<math> \frac{d^2\ln\rho}{dr^2} +\frac{2}{r} \frac{d\ln\rho}{dr} + \beta^2 \rho = 0 \, , </math>
where,
<math> \beta^2 \equiv \frac{4\pi G}{c_s^2} \, . </math>
This matches the governing ODE whose derivation was published on p. 131 of Robert Emden's (1907) book titled, Gaskugeln.
|
Derivation by Emden (edited) |
|
|
Note that, in Emden's derivation, <math>H</math> is not enthalpy but, rather, the effective gas constant, <math>H = c_s^2/T</math>. |
|
By adopting the following dimensionless variables,
<math> \mathfrak{r}_1 \equiv \rho_c^{1/2} \beta r \, , ~~~~\mathrm{and}~~~~v_1 \equiv \ln(\rho/\rho_c) \, , </math>
where <math>\rho_c</math> is the configuration's central density, the governing ODE can be rewritten in dimensionless form as,
<math> \frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, , </math>
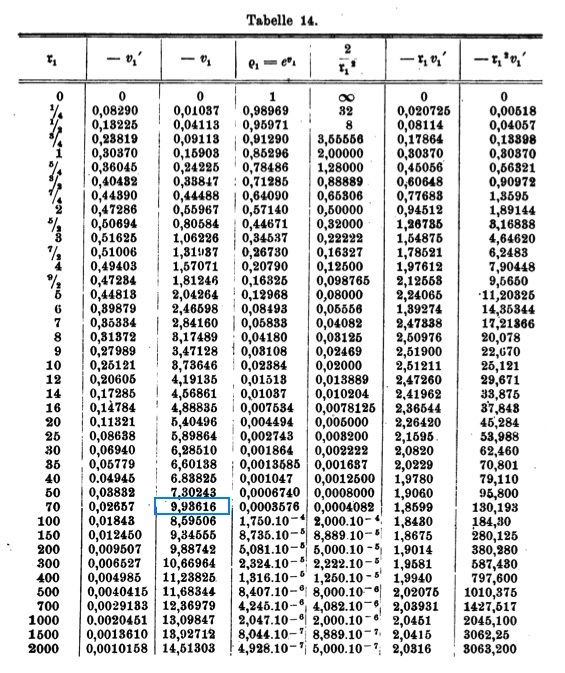
which is exactly the equation numbered (II"a) that can be found on p. 133 of Emden (1907). Emden numerically determined the behavior of the function <math>v_1(\mathfrak{r}_1)</math>, its first derivative with respect to <math>\mathfrak{r}_1</math>, <math>v_1'</math>, along with <math>e^{v_1}</math> and several other useful products, and published his results as Table 14, on p. 135 of his book. The table is reproduced here, primarily for historical purposes.
Emden's Numerical Solution
|
Note: The entry highlighted in blue in the <math>3^\mathrm{rd}</math> column must be a typesetting error. |
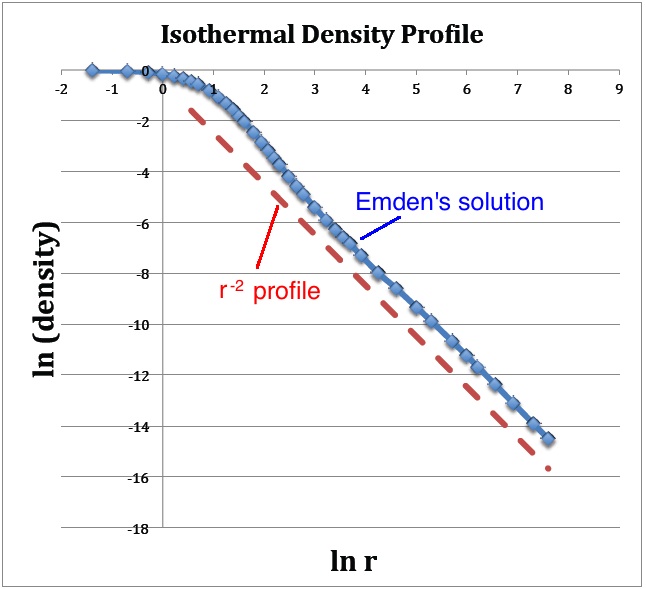
A plot of <math>v_1</math> versus <math>\ln\mathfrak{r}_1</math>, as shown below in Figure 1a, translates into a log-log plot of the equilibrium configuration's <math>\rho(r)</math> density profile. Notice that this isolated isothermal configuration extends to infinity and that, at large radii, the density profile displays a simple power-law behavior — specifically, <math> \rho \propto r^{-2}</math>. This is consistent with our general discussion, presented elsewhere, of power-law density distributions as solutions of the Lane-Emden equation.
|
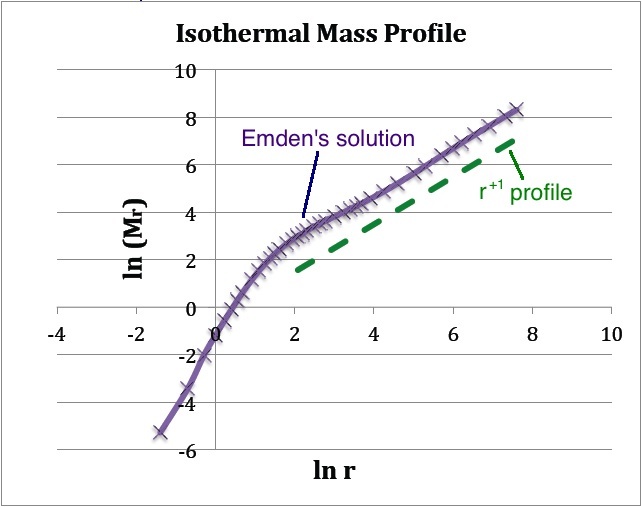
Figure 1: Emden's Numerical Solution |
|
|
(a) The <math>(x,y)</math> locations of the data points plotted in blue are drawn directly from column 1 and column 3 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = v_1</math>. The dashed red line has a slope of <math>-2</math> and serves to illustrate that, at large radii, the isothermal density profile tends toward a <math>\rho \propto r^{-2}</math> distribution. |
(b) The <math>(x,y)</math> locations of the data points plotted in purple are drawn directly from column 1 and column 7 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = \mathfrak{r}_1^2 v_1'</math>. The dashed green line has a slope of <math>+1</math> and serves to illustrate that, at large radii, the isothermal <math>M(r)</math> distribution tends toward a <math>M_r \propto r</math> distribution. |
Mass Profile
The mass enclosed within a given radius, <math>M_r</math>, can be determined by performing an appropriate volume-weighted integral over the density distribution. Specifically, based on the key expression for,
in spherically symmetric configurations, the relevant integral is,
<math> M_r = \int_0^r 4\pi r^2 \rho(r) dr \, . </math>
But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for
in a spherically symmetric configuration. Since, for an isothermal equation of state (see above),
<math> \frac{dP}{\rho} = c_s^2 {d\ln\rho} \, , </math>
the statement of hydrostatic balance can be rewritten as,
<math> M_r = \frac{c_s^2}{G} \biggl[ - r^2 \frac{d\ln\rho}{dr} \biggr] = \frac{c_s^2}{G \rho_c^{1/2} \beta} \biggl[ - \mathfrak{r}_1^2 \frac{dv_1}{d\mathfrak{r}_1} \biggr] = \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \mathfrak{r}_1^2 v_1' \biggr] \, . </math>
The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square brackets of this last expression; having units of mass, the coefficient out front sets the mass scale of the equilibrium configuration and depends only on the choice of central density and isothermal sound speed. Hence, a plot of <math>\ln(\mathfrak{r}_1^2 v_1')</math> versus <math>\ln\mathfrak{r}_1</math>, as shown above in Figure 1b, translates into a log-log plot of the equilibrium configuration's <math>M_r</math> mass profile. Notice that, along with the radius, the mass of this isolated isothermal configuration extends to infinity and that, at large radii, the mass profile displays a simple power-law behavior — specifically, <math> M_r \propto r^{+1}</math>.
As was realized independently by Ebert (1955) and Bonnor (1956), a spherically symmetric isothermal equilibrium configuration of finite radius and finite mass can be constructed if the system is embedded in a pressure-confining external medium. We discuss their findings elsewhere.
Summary
Based on the above derivations, the internal structural properties of an equilibrium isothermal sphere can be described in terms of the tabulated quantities provided in Emden's Table 14 as follows:
- Radial Coordinate Position:
- Given the isothermal sound speed, <math>c_s</math>, and the central density, <math>\rho_c</math>, the radial coordinate is,
<math>r = ( \rho_c \beta^2 )^{-1/2} \mathfrak{r}_1 = \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \mathfrak{r}_1 </math> .
- Density & Pressure:
- As a function of the radial coordinate, <math>r(\mathfrak{r}_1)</math>, the density profile is,
<math>\rho(r(\mathfrak{r}_1))= \rho_c v_1(\mathfrak{r}_1)</math>;
- and the pressure profile is,
<math>P(r(\mathfrak{r}_1))= (c_s^2 \rho_c) v_1(\mathfrak{r}_1)</math>.
- Mass:
- Given <math>c_s</math> and <math>\rho_c</math>, the natural mass scale is,
<math>M_0 \equiv \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} </math> ;
- and, expressed in terms of <math>M_0</math>, the mass that lies interior to radius <math>r</math> is,
<math> M_r = M_0 [ - \mathfrak{r}_1^2 v_1' ] \, . </math>
- Enthalpy & Gravitational Potential:
- To within an additive constant, the enthalpy distribution is,
<math>H(r(\mathfrak{r}_1))= c_s^2 \ln[v_1(\mathfrak{r}_1)]</math>;
- and the gravitational potential is,
<math>\Phi(r(\mathfrak{r}_1)) = - H(r(\mathfrak{r}_1))= - c_s^2 \ln[v_1(\mathfrak{r}_1)]</math>.
- Mass-Radius relationship:
- STILL TO BE WRITTEN! We see that, for a given value of <math>\rho_c</math>, the relationship between the configuration's total mass and radius is,
<math>M \propto R^3 ~~~~~\mathrm{or}~~~~~R \propto M^{1/3} </math> .
- Central- to Mean-Density Ratio:
- STILL TO BE WRITTEN! The ratio of the configuration's central density to its mean density is,
<math>\frac{\rho_c}{\bar{\rho}} = \biggl(\frac{\pi M}{4 R^3} \biggr)\biggl(\frac{3 M}{4 \pi R^3} \biggr) = \frac{\pi^2}{3} </math> .
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |