Difference between revisions of "User:Tohline/SSC/Structure/IsothermalSphere"
(→Emden's Numerical Solution: Discuss figure 1) |
(→Emden's Numerical Solution: Explain calculation of mass) |
||
| Line 101: | Line 101: | ||
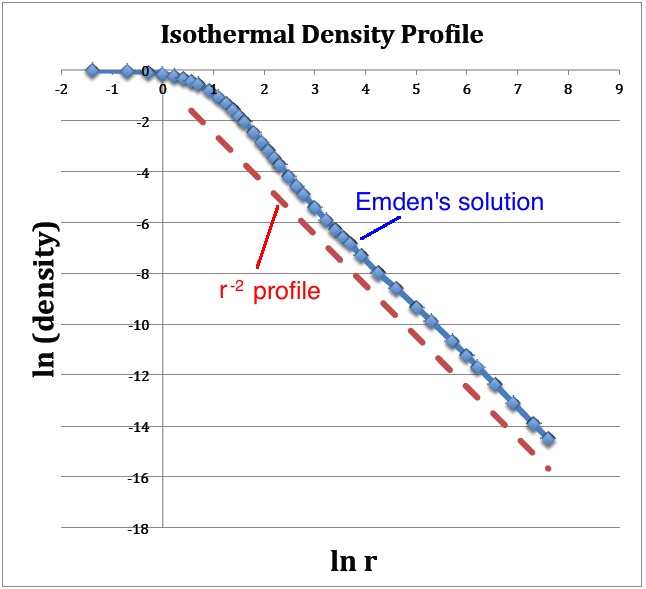
A plot of <math>v_1</math> versus <math>\ln\mathfrak{r}_1</math>, as shown below in Figure 1a, translates into a log-log plot of the equilibrium configuration's <math>\rho(r)</math> density profile. Notice that this isolated isothermal configuration extends to infinity and that, at large radii, the density profile displays a simple power-law behavior — specifically, <math> \rho \propto r^{-2}</math>. This is consistent with our general discussion, [[User:Tohline/SSC/Structure/PowerLawDensity|presented elsewhere]], of power-law density distributions as solutions | A plot of <math>v_1</math> versus <math>\ln\mathfrak{r}_1</math>, as shown below in Figure 1a, translates into a log-log plot of the equilibrium configuration's <math>\rho(r)</math> density profile. Notice that this isolated isothermal configuration extends to infinity and that, at large radii, the density profile displays a simple power-law behavior — specifically, <math> \rho \propto r^{-2}</math>. This is consistent with our general discussion, [[User:Tohline/SSC/Structure/PowerLawDensity|presented elsewhere]], of power-law density distributions as solutions of the Lane-Emden equation. | ||
<div align="center"> | <div align="center"> | ||
| Line 139: | Line 130: | ||
</table> | </table> | ||
</div> | </div> | ||
==Mass Profile== | |||
The mass enclosed within a given radius, <math>M_r</math>, can be determined by performing an appropriate volume-weighted integral over the density distribution. Specifically, based on the key expression for, | |||
<div align="center"> | |||
<span id="HydrostaticBalance"><font color="#770000">'''Mass Conservation'''</font></span><br /> | |||
{{User:Tohline/Math/EQ_SSmassConservation01}} | |||
</div> | |||
in spherically symmetric configurations, the relevant integral is, | |||
<div align="center"> | |||
<math> | |||
M_r = \int_0^r 4\pi r^2 \rho(r) dr \, . | |||
</math> | |||
</div> | |||
But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for, | |||
<div align="center"> | |||
<span id="HydrostaticBalance"><font color="#770000">'''Hydrostatic Balance'''</font></span><br /> | |||
{{User:Tohline/Math/EQ_SShydrostaticBalance01}} | |||
</div> | |||
in a spherically symmetric configuration. As described above, for the isothermal equation of state being considered here, | |||
<div align="center"> | |||
<math> | |||
\frac{dP}{\rho} = c_s^2 {d\ln\rho} \, . | |||
</math> | |||
</div> | |||
Hence, the statement of hydrostatic balance can be rewritten as, | |||
<div align="center"> | |||
<math> | |||
M_r = \frac{c_s^2}{G} \biggl[ - r^2 \frac{d\ln\rho}{dr} \biggr] = \frac{c_s^2}{G \rho_c^{1/2} \beta} \biggl[ - \mathfrak{r}_1^2 \frac{dv_1}{d\mathfrak{r}_1} \biggr] | |||
= \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \mathfrak{r}_1^2 v_1' \biggr] \, . | |||
</math> | |||
</div> | |||
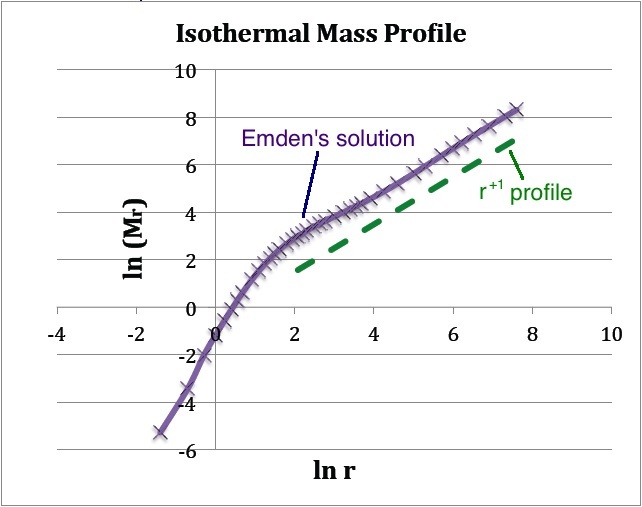
The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square brakets of this last expression; the coefficient out front, which depends only on the choice of central density and isothermal sound speed, has units of mass. Hence, a plot of <math>\ln(\mathfrak{r}_1^2 v_1')</math> versus <math>\ln\mathfrak{r}_1</math>, as shown above in Figure 1b, translates into a log-log plot of the equilibrium configuration's <math>M_r</math> mass profile. Notice that, along with the radius, the mass of this isolated isothermal configuration extends to infinity and that, at large radii, the mass profile displays a simple power-law behavior — specifically, <math> M_r \propto r^{+1}</math>. | |||
As was noticed indepenedently by [[User:Tohline/SSC/Structure/BonnorEbert|Ebert (1955) and Bonnor (1956)]], a spherically symmetric isothermal equilibrium configuration of finite radius and finite mass can be constructed if the system is embedded in a pressure-confining external medium. | |||
==Bonnor and Ebert== | ==Bonnor and Ebert== | ||
Revision as of 19:36, 31 October 2012

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal Sphere (structure)
Here we supplement the simplified set of principal governing equations with an isothermal equation of state, that is, <math>~P</math> is related to <math>~\rho</math> through the relation,
<math>P = c_s^2 \rho \, ,</math>
where, <math>c_s</math> is the isothermal sound speed. Comparing this <math>~P</math>-<math>~\rho</math> relationship to
Form A
of the Ideal Gas Equation of State,
|
<math>~P_\mathrm{gas} = \frac{\Re}{\bar{\mu}} \rho T</math> |
we see that,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} = \frac{k T}{m_u \bar{\mu}} \, ,</math>
where, <math>~\Re</math>, <math>~k</math>, <math>~m_u</math>, and <math>~\bar{\mu}</math> are all defined in the accompanying variables appendix. It will be useful to note that, for an isothermal gas, <math>~H</math> is related to <math>~\rho</math> via the expression,
<math> dH = \frac{dP}{\rho} = c_s^2 d\ln\rho \, . </math>
Governing Relations
Adopting solution technique #2, we need to solve the following second-order ODE relating the two unknown functions, <math>~\rho</math> and <math>~H</math>:
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{dH}{dr} \biggr) =- 4\pi G \rho</math> .
Using the <math>~H</math>-<math>~\rho</math> relationship for an isothermal gas presented above, this can be rewritten entirely in terms of the density as,
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\ln\rho}{dr} \biggr) =- \frac{4\pi G}{c_s^2} \rho \, ,</math>
or, equivalently,
<math> \frac{d^2\ln\rho}{dr^2} +\frac{2}{r} \frac{d\ln\rho}{dr} + \beta^2 \rho = 0 \, , </math>
where,
<math> \beta^2 \equiv \frac{4\pi G}{c_s^2} \, . </math>
This matches the governing ODE whose derivation was published on p. 131 of Robert Emden's (1907) book titled, Gaskugeln.
|
Derivation by Emden (edited) |
|
By adopting the following dimensionless variables,
<math> \mathfrak{r}_1 \equiv \rho_c^{1/2} \beta r \, , ~~~~\mathrm{and}~~~~v_1 \equiv \ln(\rho/\rho_c) \, , </math>
where <math>\rho_c</math> is the configuration's central density, the governing ODE can be rewritten in dimensionless form as,
<math> \frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, , </math>
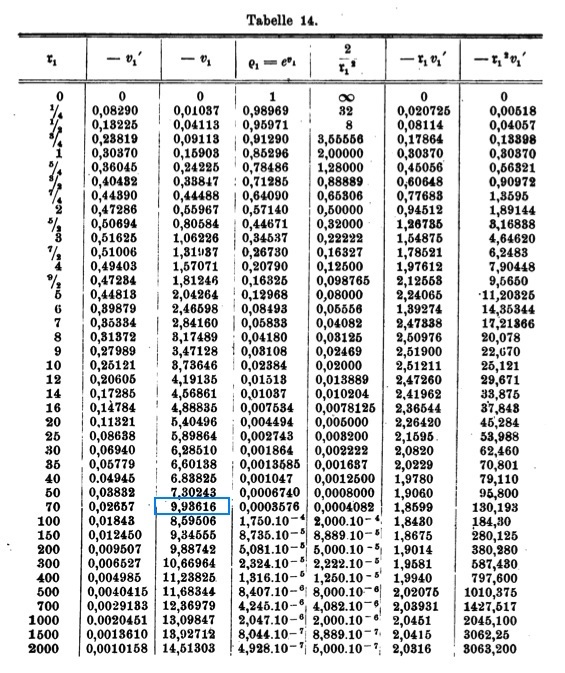
which is exactly the equation numbered (II"a) that can be found on p. 133 of Emden (1907). Emden numerically determined the behavior of the function <math>v_1(\mathfrak{r}_1)</math>, its first derivative with respect to <math>\mathfrak{r}_1</math>, <math>v_1'</math>, along with <math>e^{v_1}</math> and several other useful products, and published his results as Table 14, on p. 135 of his book. The table is reproduced here, primarily for historical purposes.
Emden's Numerical Solution
|
Note: The entry highlighted in blue in the <math>3^\mathrm{rd}</math> column must be a typesetting error. |
A plot of <math>v_1</math> versus <math>\ln\mathfrak{r}_1</math>, as shown below in Figure 1a, translates into a log-log plot of the equilibrium configuration's <math>\rho(r)</math> density profile. Notice that this isolated isothermal configuration extends to infinity and that, at large radii, the density profile displays a simple power-law behavior — specifically, <math> \rho \propto r^{-2}</math>. This is consistent with our general discussion, presented elsewhere, of power-law density distributions as solutions of the Lane-Emden equation.
|
Figure 1: Emden's Numerical Solution |
|
|
(a) The <math>(x,y)</math> locations of the data points plotted in blue are drawn directly from column 1 and column 3 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = v_1</math>. The dashed red line has a slope of <math>-2</math> and serves to illustrate that, at large radii, the isothermal density profile tends toward a <math>\rho \propto r^{-2}</math> distribution. |
(b) The <math>(x,y)</math> locations of the data points plotted in purple are drawn directly from column 1 and column 7 of Emden's Table 14 — specifically, <math>x = \ln(\mathfrak{r}_1)</math> and <math>y = \mathfrak{r}_1^2 v_1'</math>. The dashed green line has a slope of <math>+1</math> and serves to illustrate that, at large radii, the isothermal <math>M(r)</math> distribution tends toward a <math>M_r \propto r</math> distribution. |
Mass Profile
The mass enclosed within a given radius, <math>M_r</math>, can be determined by performing an appropriate volume-weighted integral over the density distribution. Specifically, based on the key expression for,
in spherically symmetric configurations, the relevant integral is,
<math> M_r = \int_0^r 4\pi r^2 \rho(r) dr \, . </math>
But <math>M_r</math> also can be determined from the information provided in column 7 of Emden's Table 14 — that is, from knowledge of the first derivative of <math>v_1</math>. The appropriate expression can be obtained from the mathematical prescription for,
in a spherically symmetric configuration. As described above, for the isothermal equation of state being considered here,
<math> \frac{dP}{\rho} = c_s^2 {d\ln\rho} \, . </math>
Hence, the statement of hydrostatic balance can be rewritten as,
<math> M_r = \frac{c_s^2}{G} \biggl[ - r^2 \frac{d\ln\rho}{dr} \biggr] = \frac{c_s^2}{G \rho_c^{1/2} \beta} \biggl[ - \mathfrak{r}_1^2 \frac{dv_1}{d\mathfrak{r}_1} \biggr] = \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ - \mathfrak{r}_1^2 v_1' \biggr] \, . </math>
The quantity tabulated in column 7 of Emden's Table 14 is precisely the dimensionless term inside the square brakets of this last expression; the coefficient out front, which depends only on the choice of central density and isothermal sound speed, has units of mass. Hence, a plot of <math>\ln(\mathfrak{r}_1^2 v_1')</math> versus <math>\ln\mathfrak{r}_1</math>, as shown above in Figure 1b, translates into a log-log plot of the equilibrium configuration's <math>M_r</math> mass profile. Notice that, along with the radius, the mass of this isolated isothermal configuration extends to infinity and that, at large radii, the mass profile displays a simple power-law behavior — specifically, <math> M_r \propto r^{+1}</math>.
As was noticed indepenedently by Ebert (1955) and Bonnor (1956), a spherically symmetric isothermal equilibrium configuration of finite radius and finite mass can be constructed if the system is embedded in a pressure-confining external medium.
Bonnor and Ebert
In their studies of pressure-bounded isothermal spheres, Ebert (1955, ZA, 37, 217) and Bonnor (1956, MNRAS, 116, 351) both started with this governing ODE, but developed its solution in different ways. Here we present both developments while highlighting transformations between the two.
| Derivation by Bonnor (edited) | translation | Derivation by Ebert (edited) |
| <math>G \Leftrightarrow \gamma</math> | ||
| <math>\rho_c \Leftrightarrow \rho_0</math> | ||
| <math>\frac{kT}{m} \Leftarrow c_s^2 \Rightarrow \frac{\Re T_0}{\mu}</math> | ||
| <math>\beta^{1/2}\lambda^{-1/2} \Leftrightarrow l_0</math> | ||
| <math>e^{-\psi} \Leftrightarrow \eta</math> |
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |