Difference between revisions of "User:Tohline/SSC/Structure/BonnorEbert"
(→Maximum Mass: Expand on discussion of maximum mass) |
(→Maximum Mass: Correct wrong numbers copied from Emden's table and elaborate further) |
||
| Line 78: | Line 78: | ||
</div> | </div> | ||
An isothermal sphere that is truncated at this location will have a radius, | |||
<div align="center"> | |||
<math> | |||
R = \biggl( \frac{c_s^2}{G\rho_c} \biggr)^{1/2} \frac{6.5}{\sqrt{4\pi}} = 1.8 \biggl( \frac{c_s^2}{G\rho_c} \biggr)^{1/2} \, , | |||
</math> | |||
</div> | |||
which matches equation (3.3) of Bonnor (1956), and it will have a total mass, | |||
<div align="center"> | |||
<math>M_r = \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} [-r_1^2 v'_1 ] \approx | |||
\biggl( \frac{c_s^6}{G^3 \rho_c} \biggr)^{1/2} \biggl[ \frac{(14.353+17.214)/2}{\sqrt{4\pi}} \biggr] = | |||
4.45 \biggl( \frac{c_s^6}{G^3 \rho_c} \biggr)^{1/2}\, .</math> | |||
</div> | |||
In order to maintain an equilibrium structure while truncating the isothermal model at this radius requires applying an external pressure equal to <math>P(\xi)</math>, that is, | In order to maintain an equilibrium structure while truncating the isothermal model at this radius requires applying an external pressure equal to <math>P(\xi)</math>, that is, | ||
<div align="center"> | <div align="center"> | ||
<math>P_e = \bar{c_s}^2 \rho_c e^{v_1} \approx \bar{c_s}^2 \rho_c (0.08493 + 0.05833)/2 = 0.0716~ \bar{c_s}^2 \rho_c \, .</math> | <math>P_e = \bar{c_s}^2 \rho_c e^{v_1} \approx \bar{c_s}^2 \rho_c (0.08493 + 0.05833)/2 = 0.0716~ \bar{c_s}^2 \rho_c \, .</math> | ||
</div> | </div> | ||
Eliminating <math>\rho_c</math> between these last two expressions gives, | |||
Eliminating <math>\rho_c</math> between these two expressions gives, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5"> | <table border="0" cellpadding="5"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>M_\mathrm{max}</math> | ||
</td> | </td> | ||
<td align="center">=</td> | <td align="center">=</td> | ||
| Line 106: | Line 114: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \frac{1}{2\pi^{1/2}} \biggl\{ \frac{1}{2} \biggl[ | \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \frac{1}{2\pi^{1/2}} \biggl\{ \frac{1}{2} \biggl[ 14.353 (0.08493)^{1/2} + | ||
17.214 (0.05833)^{1/2} \biggr] \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 119: | Line 127: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
1.17 \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 125: | Line 133: | ||
</table> | </table> | ||
</div> | </div> | ||
This is the mass upper limit — the so-called Bonnor-Ebert mass — for a stable, pressure-bounded isothermal sphere. | |||
[[User:Tohline/SSC/Structure/LimitingMasses#Bounded_Isothermal_Sphere_.26_Bonnor-Ebert_Mass|In a separate discussion]], we compare this result to the determinations of other related mass upper-limits. | |||
=Related Wikipedia Discussions= | =Related Wikipedia Discussions= | ||
Revision as of 19:50, 2 June 2013
Pressure-Bounded Isothermal Sphere

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As has been derived and discussed elsewhere, an isolated isothermal sphere has a density profile that extends to infinity and, correspondingly, an unbounded total mass. In an astrophysical context, neither of these properties is desirable. A more realistic isothermal configuration can be constructed by embedding the structure in a low density, but hot external medium whose pressure, <math>P_e</math>, confines the isothermal configuration to a finite size. In a mathematical model, this can be accomplished by ripping off an outer layer of the isolated isothermal configuration down to the radius — label it <math>\xi_e</math> — at which the configuration's original (internal) pressure equals <math>P_e</math>; the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should be unaltered and in equilibrium. (This will work only for spherically symmetric configurations, as the gravitational acceleration at any location only depends on the mass contained inside that radius.) Ebert (1955) and Bonnor (1956) are credited with constructing the first such models and, most significantly, discovering that, for any specified sound speed and applied external pressure, there is a mass above which no equilibrium configuration exists. We present, here, the salient elements of these (essentially equivalent) derivations.
Prior to studying this discussion of pressure-bounded isothermal spheres, we recommend studying our related discussion of pressure-bounded <math>~n</math> = 5 polytropes. As with isolated isothermal spheres, isolated <math>~n</math> = 5 polytropes extend to infinity. But, unlike their isothermal counterparts, the structure of <math>~n</math> = 5 polytropes is describable analytically. Hence, an analysis of their structure and its extension to pressure-bounded configurations avoids the clutter introduced by a model — such as the isothermal sphere — that can only be described numerically. As it turns out, the pressure-bounded <math>~n</math> = 5 polytrope exhibits a Bonnor-Ebert type limiting mass that is analytically prescribable. Its derivation is mathematically quite clean and provides a firm foundation for understanding the better known — but only numerically prescribable — Bonnor-Ebert limiting mass.
Governing Relation
The equilibrium structure of an isolated isothermal sphere, as derived by Emden (1907), has been discussed elsewhere. From this separate discussion we appreciate that the governing ODE is,
<math>\frac{1}{r^2} \frac{d}{dr}\biggl( r^2 \frac{d\ln\rho}{dr} \biggr) =- \frac{4\pi G}{c_s^2} \rho \, ,</math>
where,
<math>c_s^2 = \frac{\Re T}{\bar{\mu}} = \frac{k T}{m_u \bar{\mu}} \, ,</math>
is the square of the isothermal sound speed. In their studies of pressure-bounded isothermal spheres, Ebert (1955, ZA, 37, 217) and Bonnor (1956, MNRAS, 116, 351) both started with this governing ODE, but developed its solution in different ways. Here we present both developments while highlighting transformations between the two.
| Derivation by Bonnor (edited) | translation | Derivation by Ebert (edited) |
| <math>G \Leftrightarrow \gamma</math> | ||
| <math>\rho_c \Leftrightarrow \rho_0</math> | ||
| <math>\frac{kT}{m} \Leftarrow c_s^2 \Rightarrow \frac{\Re T_0}{\mu}</math> | ||
| <math>\beta^{1/2}\lambda^{-1/2} \Leftrightarrow l_0</math> | ||
| <math>e^{-\psi} \Leftrightarrow \eta</math> |
Both of these dimensionless governing ODEs — Bonnor's Eq. (2.8) and Ebert's Eq. (17) — are identical to the dimensionless expression derived by Emden (see the presentation elsewhere), namely,
<math> \frac{d^2v_1}{d\mathfrak{r}_1^2} +\frac{2}{\mathfrak{r}_1} \frac{dv_1}{dr} + e^{v_1} = 0 \, . </math>
The translation from Emden-to-Bonnor-to-Ebert is straightforward:
<math> \mathfrak{r}_1 = \xi|_\mathrm{Bonner} = \xi|_\mathrm{Ebert}~~~~\mathrm{and}~~~~e^{v_1} = e^{-\psi} = \eta \, . </math>
Maximum Mass
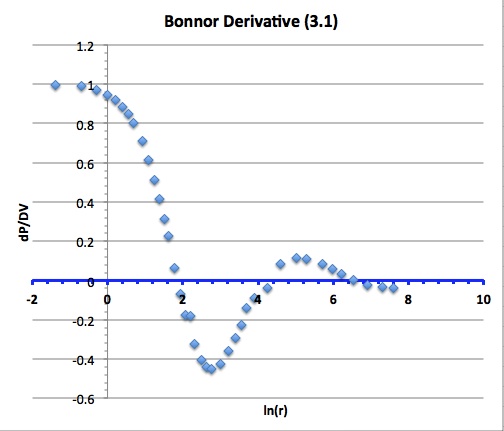
As is shown in his equation (3.1), Bonnor (1956) determined that <math>(dP/dV)_{N,T}</math> goes to zero when,
<math>1-\frac{1}{2} e^{\psi} \biggl( \frac{d\psi}{d\xi}\biggr)^2 = 0 \, .</math>
In the following figure, the function defined by the left-hand-side of this expression is plotted versus <math>\ln\xi</math> using Emden's (1907) tabulated data. As Bonnor noted, the function first crosses zero when <math>\xi \approx 6.5</math> (<math>\ln\xi = 1.87</math>).
An isothermal sphere that is truncated at this location will have a radius,
<math> R = \biggl( \frac{c_s^2}{G\rho_c} \biggr)^{1/2} \frac{6.5}{\sqrt{4\pi}} = 1.8 \biggl( \frac{c_s^2}{G\rho_c} \biggr)^{1/2} \, , </math>
which matches equation (3.3) of Bonnor (1956), and it will have a total mass,
<math>M_r = \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} [-r_1^2 v'_1 ] \approx \biggl( \frac{c_s^6}{G^3 \rho_c} \biggr)^{1/2} \biggl[ \frac{(14.353+17.214)/2}{\sqrt{4\pi}} \biggr] = 4.45 \biggl( \frac{c_s^6}{G^3 \rho_c} \biggr)^{1/2}\, .</math>
In order to maintain an equilibrium structure while truncating the isothermal model at this radius requires applying an external pressure equal to <math>P(\xi)</math>, that is,
<math>P_e = \bar{c_s}^2 \rho_c e^{v_1} \approx \bar{c_s}^2 \rho_c (0.08493 + 0.05833)/2 = 0.0716~ \bar{c_s}^2 \rho_c \, .</math>
Eliminating <math>\rho_c</math> between these last two expressions gives,
|
<math>M_\mathrm{max}</math> |
= |
<math>\biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2}\biggl[ \frac{1}{4\pi}\biggr]^{1/2} (- r_1^2 v'_1 e^{v_1/2} )</math> |
|
|
<math>\approx</math> |
<math> \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \frac{1}{2\pi^{1/2}} \biggl\{ \frac{1}{2} \biggl[ 14.353 (0.08493)^{1/2} + 17.214 (0.05833)^{1/2} \biggr] \biggr\} </math> |
|
|
<math>\approx</math> |
<math> 1.17 \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \, . </math> |
This is the mass upper limit — the so-called Bonnor-Ebert mass — for a stable, pressure-bounded isothermal sphere. In a separate discussion, we compare this result to the determinations of other related mass upper-limits.
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |