User:Tohline/AxisymmetricConfigurations/HSCF
Introduction

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Text colored dark green has been extracted verbatim from a relatively early review by P. A. Strittmatter (1969): The study of the internal structure of rotating stars is complicated by the necessity to introduce circulation currents and to solve Poisson's equation in two dimensions with an unknown boundary to the density distribution … With the advent of large-capacity, fast computers it has become possible to tackle the problem by direct numerical integration of the appropriate partial-differential equations. This method has been adopted by R. A. James (1964) in considering uniformly rotating polytopes and by R. Stoeckly (1965) who treated the case when the rotation velocity <math>~\Omega</math> varies as a Gaussian function of the distance from the rotation axis … Ostriker and his collaborators (cf. J. P. Ostriker & J. W.-K. Mark 1968) have developed an approach (called, by them, the self-consistent field or SCF method) in which Poisson's equation is replaced by its formal integral solution and an iterative procedure established in which the potential is derived from a guessed density distribution. A new density distribution is then obtained from the equation of hydrostatic support … While the present author has no experience in using the SCF method, it would appear to combine considerable power with reasonable speed of application and must probably be considered the most practical method of solution so far developed.
| Table 1: Poisson Equation | ||||||
|---|---|---|---|---|---|---|
| Integral Relation | Differential Relation | |||||
|
|
|||||
In this paragraph, teal-colored text has been extracted verbatim from §II.b of J. P. Ostriker and J. W.-K. Mark (1968, ApJ, 151, 1075 - 1088): … we shall alternately solve each of the two problems as exactly as numerical techniques permit, and then iterate to obtain self-consistency.
i) <math>~\rho(\vec{x})</math> <math>~\xrightarrow{~~~~~\mathrm{potential ~theory}~~~~~~} ~ \Phi(\vec{x})</math>
ii) <math>~\Phi(\vec{x})+\Psi(\varpi) ~\xrightarrow{~~~\mathrm{equilibrium ~condition}~~} ~ \rho(\vec{x})</math>
The integral relation between potential and density — as opposed to the differential relation, see Table 1 — encourages us to think that a "bad" density will, in step (i), lead to a "good" potential, which, by step (ii), will yield a "good" density which when substituted in (i) produces a "very good" potential, etc. The method works. It should be noted that an SCF approach is commonly used for determining molecular structure under the name Hartree-Fock.
Hachisu Self-Consistent-Field Technique
I. Hachisu |
|---|
In 1986, Izumi Hachisu published two papers in The Astrophysical Journal Supplement Series (vol. 61, pp. 479-507, and vol. 62, pp. 461-499) describing "A Versatile Method for Obtaining Structures of Rapidly Rotating Stars." (Henceforth, we will refer to this method as the Hachisu Self-Consistent-Field, or HSCF, technique.) The HSCF technique has been built upon — and has further improved — the SCF method introduced by J. P. Ostriker & J. W.-K. Mark (1968). We have found the HSCF technique to be an extremely powerful tool for constructing equilibrium configurations of self-gravitating fluid systems under a wide variety of different circumstances. The photo of Professor Izumi Hachisu shown here, on the left, dates from the mid-1980s — about the time he developed this remarkably useful numerical technique; a more recent photo can be found on the web page associated with Professor Hachisu's current faculty appointment at the University of Tokyo, Komaba.
Constructing Two-Dimensional, Axisymmetric Structures
As has been explained in an accompanying discussion, our objective is to solve an algebraic expression for hydrostatic balance,
<math>~H + \Phi + \Psi = C_0</math> ,
in conjunction with the Poisson equation in a form that is appropriate for two-dimensional, axisymmetric systems, namely,
<math>~ \frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho . </math>
Steps to Follow
|
- Choose a particular barotropic equation of state. More specifically, functionally define the density-enthalpy relationship, <math>~\rho(H)</math>, and identify what value, <math>~H_\mathrm{surface}</math>, the enthalpy will have at the surface of your configuration. For example, if a polytropic equation of state is adopted, <math>~H_\mathrm{surface} = 0</math> is a physically reasonable prescription.
- Choosing from, for example, a list of astrophysically relevant simple rotation profiles, specify the corresponding functional form of the centrifugal potential, <math>~\Psi(\varpi)</math>, that will define the radial distribution of specific angular momentum in your equilibrium configuration. If the choice is uniform rotation, then <math>~\Psi = - \varpi^2 \omega_0^2/2 \, ,</math> where <math>~\omega_0</math> is a constant to be determined.
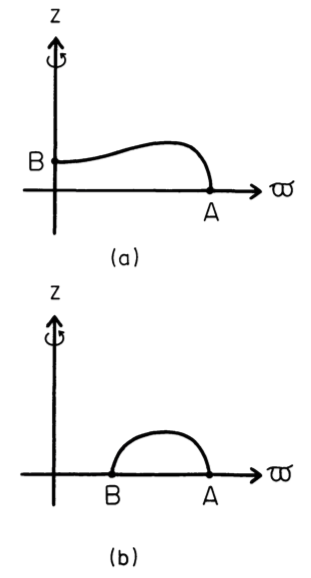
- On your chosen computational lattice — for example, on a cylindrical-coordinate mesh — identify two boundary points, A and B, that will lie on the surface of your equilibrium configuration. These two points should remain fixed in space during the HSCF iteration cycle and ultimately will confine the volume and define the geometry of the derived equilibrium object. Note that, by definition, the enthalpy at these two points is, <math>~H_A = H_B = H_\mathrm{surface}</math>.
- Throughout the volume of your computational lattice, guess a trial distribution of the mass density, <math>~\rho(\varpi,z)</math>, such that no material falls outside a volume defined by the two boundary points, A and B, that were identified in Step #3. Usually an initially uniform density distribution will suffice to start the SCF iteration.
- Via some accurate numerical algorithm, solve the Poisson equation to determine the gravitational potential, <math>~\Phi(\varpi,z)</math>, throughout the computational lattice corresponding to the trial mass-density distribution that was specified in Step #4 (or in Step #9).
- From the gravitational potential determined in Step #5, identify the values of <math>~\Phi_A</math> and <math>~\Phi_B</math> at the two boundary points that were selected in Step #3.
- From the "known" values of the enthalpy (Step #3) and the gravitational potential (Step #6) at the two selected surface boundary points A and B, determine the values of the constants, <math>~C_0</math> and <math>~\omega_0</math>, that appear in the algebraic equation that defines hydrostatic equilibrium.
- From the most recently determined values of the gravitational potential, <math>~\Phi(\varpi,z)</math> (Step #5), and the values of the two constants, <math>~C_0</math> and <math>~\omega_0</math> just determined (Step #7), determine the enthalpy distribution throughout the computational lattice.
- From <math>~H(\varpi,z)</math> and the selected barotropic equation of state (Step #1), calculate an "improved guess" of the density distribution, <math>~\rho(\varpi,z)</math>, throughout the computational lattice.
- Has the model converged to a satisfactory equilibrium solution? (Usually a satisfactory solution has been achieved when the derived model parameters — for example, the values of <math>~C_0</math> and <math>~\omega_0</math> — change very little between successive iterations and the viral error is sufficiently small.)
- If the answer is, "NO": Repeat steps 5 through 10.
- If the answer is, "YES": Stop iteration.
Related Discussions
Reviews
- P. A. Strittmatter (1969, Annual Review of Astronomy and Astrophysics, 7, 665 - 684) — Stellar Rotation
- N. R. Lebovitz (1967, Annual Review of Astronomy and Astrophysics, 5, 465 - 480) — Rotating Fluid Masses
Solution Methods
- Y. Eriguchi & E. Mueller (1985, A&A, 146, 260 - 268) — A General Computational Method for Obtaining Equilibria of Self-Gravitating and Rotating Gases
- S. W. Stahler (1983, ApJ, 268, 155 - 184) — The Equilibria of Rotating, Isothermal Clouds. I. - Method of Solution
- Y. Eriguchi (1978, PASJ, 30, 507 - 518) — Hydrostatic Equilibria of Rotating Polytropes
- S. I. Blinnikov (1975, Soviet Astronomy, 19, 151 - 156) — Self-Consistent Field Method in the Theory of Rotating Stars
- M. J. Clement (1974, ApJ, 194, 709 - 714) — On the Solution of Poisson's Equation for Rapidly Rotating Stars
- S. Jackson (1970, ApJ, 161, 579 - 585) — Rapidly Rotating Stars. V. The Coupling of the Henyey and the Self-Consistent Methods
- J. P. Ostriker & J. W.-K. Mark (1968, ApJ, 151, 1075 - 1088) — Rapidly Rotating Stars. I. The Self-Consistent-Field Method
- R. A. James (1964, ApJ, 140, 552 - 582) — The Structure and Stability of Rotating Gas Masses
Early Eriguchi Applications
- Y. Eriguchi & E. Mueller (1985, A&A, 147, 161 - 168) — Equilibrium Models of Differentially Rotating Polytropes and the Collapse of Rotating Stellar Cores
- I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 497 - 503) — Bifurcation Points on the Maclaurin Sequence
- I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 259 - 276) — Binary Fluid Star
- I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 239 - 257) — Fission of Dumbbell Equilibrium and Binary State of Rapidly Rotating Polytropes
- I. Hachisu & Y. Eriguchi (1983, MNRAS, 204, 583 - 589) — Bifurcations and Phase Transitions of Self-Gravitating and Uniformly Rotating Fluid
- I. Hachisu & Y. Eriguchi (1982, Prog. Theor. Phys., 68, 206 - 221) — Bifurcation and Fission of Three Dimensional, Rigidly Rotating and Self-Gravitating Polytropes
- I. Hachisu, Y. Eriguchi, & D. Sugimoto (1982, Prog. Theor. Phys., 68, 191 - 205) — Rapidly Rotating Polytropes and Concave Hamburger Equilibrium
- Y. Eriguchi & D. Sugimoto (1981, Prog. Theor. Phys., 65, 1870 - 1875) — Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid
- T. Fukushima, Y. Eriguchi, D. Sugimoto, G. S. Bisnovatyi-Kogan (1980, Prog. Theor. Phys., 63, 1957 - 1970) — Concave Hamburger Equilibrium of Rotating Bodies
Other Example Applications
- E. Mueller & Y. Eriguchi (1985, A&A, 152, 325 - 335) — Equilibrium Models of Differentially Rotating, Completely Catalyzed, Zero-Temperature Configurations With Central Densities Intermediate to White Dwarf and Neutron Star Densities
- J. R. Ipser & R. A. Managan (1981, ApJ, 250, 362 - 372) — On the Existence and Structure of Inhomogeneous Analogs of the Dedekind and Jacobi Ellipsoids
- C. T. Cunningham (1977, ApJ, 211, 568 - 578) — Rapidly Rotating Spheroids of Polytropic Index n = 1
- R. H. Durisen (1975, ApJ, 199, 179 - 183) — Upper Mass Limits for Stable Rotating White Dwarfs
- P. Bodenheimer & J. P. Ostriker (1973, ApJ, 180, 159 - 170) — Rapidly Rotating Stars. VIII. Zero-Viscosity Polytropic Sequences'
- P. Bodenheimer (1971, ApJ, 167, 153 - 163) — Rapidly Rotating Stars. VII. Effects of Angular Momentum on Upper-Main-Sequence Models
- P. Bodenheimer & J. P. Ostriker (1970, ApJ, 161, 1101 - 1113) — Rapidly Rotating Stars. VI. Pre-Main-Sequence Evolution of Massive Stars
- R. Kippenhahn & H.-C. Thomas (1970) in Proceedings of the 4th IAU Colloquium, held at the Ohio State University, Columbus, Ohio, September 8 - 11, 1969, Dordrecht: Riedel Publishing Co., edited by A. Slettebak — Stellar Rotation ==> Purchase proceedings from Springer, from Australia, or from Google
- In the introductory section of his paper, S. Jackson (1970) references this article by Kippenhahn & Thomas in the context of uniformly rotating, and therefore only mildly distorted, structures.
- J. P. Ostriker & J. L. Tassoul (1969, ApJ, 155, 987 - ) — On the Oscillations and Stability of Rotating Stellar Models. II. Rapidly Rotating White Dwarfs
- M. J. Clement (1969, ApJ, 156, 1051 - 1068) — Differential Rotation in Stars on the Upper Main Sequence
- J. W.-K. Mark (1968, ApJ, 154, 627 - ) — Rapidly Rotating Stars. III. Massive Main-Sequence Stars
- J. P. Ostriker & P. Bodenheimer (1968, ApJ, 151, 1089 - ) — Rapidly Rotating Stars. II. Massive White Dwarfs
- J. Faulkner, I. W. Roxburgh, & P. A. Strittmatter (1968, ApJ, 151, 203 - 216) — Uniformly Rotating Main-Sequence Stars
- R. Stoeckly (1965, ApJ, 142, 208 - 228) — Polytropic Models with Fast, Non-Uniform Rotation
- In the introductory section of his paper, S. Jackson (1970) states that a differentially rotating polytropic structure with a rotationally induced extreme distortion was first illustrated in this article by Stoeckly.
Henyey Technique for Nonrotating Stars
- L. G. Henyey, L. Wilets, K. H. Böhm, R. Lelevier, & R. D. Levee (1959, ApJ, 129, 628 - ) — A Method for Automatic Computation of Stellar Evolution
- L. G. Henyey, J. E. Forbes, & N. L. Gould (1964, ApJ, 139, 306 - ) — A New Method of Automatic Computation of Stellar Evolution

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |