User:Tohline/Apps/RotatingPolytropes/BarmodeLinearTimeDependent
Onset of Bar-mode Instability in Initially Axisymmetric & Differentially Rotating Polytropes
|
"… the onset of instability is not very sensitive to the compressibility or angular momentum distribution of the polytrope when the models are parameterized by T/|W| — [in particular, the m = 2 barmode becomes unstable at T/|W| ∼ 0.26 - 0.28. ] The polytrope eigenfunctions are … qualitatively different from the Maclaurin eigenfunctions in one respect: they develop strong spiral arms. The spiral arms are stronger for more compressible polytropes and for polytropes whose angular momentum distributions deviate significantly from those of the Maclaurin spheroids." |
|
— Drawn from Toman, Imamura, Pickett & Durisen (1998), ApJ, 497, 370 |

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Summary circa 2000
|
This summary is drawn — largely verbatim — from a separate web page that was originally intended to highlight animation sequences produced by LSU's astrophysicsl theory group.
In the mid-1980s, using three different 3D hydrodynamic simulation tools, R. H. Durisen, R. A. Gingold, J. E. Tohline & A. P. Boss (1986) — hereafter and in the references, below, DGTB86 — followed the development to nonlinear amplitudes of a two-armed, spiral-mode instability that arises naturally in rapidly rotating, self-gravitating fluids. The particular initial model that was examined had an <math>~n = \tfrac{3}{2}</math> polytropic equation of state, an n' = 0 angular momentum distribution, and an initial ratio of rotational to gravitational potential energy T/|W| = 0.33. The simulation tools that were used at the time were relatively crude, compared to tools that are available today.
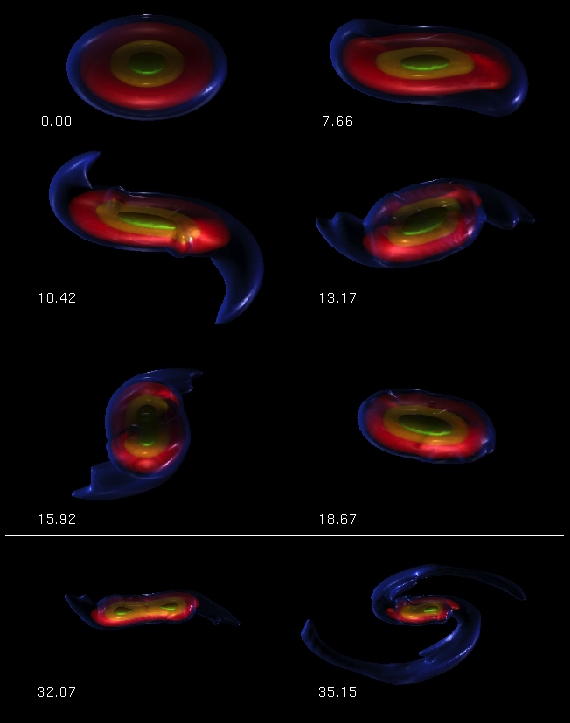
Employing a significantly improved finite-volume simulation code and improved spatial resolution (1283 grid zones), a very similar simulation has been carried out and reported by J. E. Cazes & J. E. Tohline (2000); see also the Cazes (1999) doctoral dissertation. This was done, in part, to check the validity of the earlier work and, in part, to permit us to conduct a much more thorough analysis of the end-state configuration. We will refer to this as the Model A simulation. The initial model for this simulation was constructed using the Hachisu Self-Consistent-Field (HSCF) technique; it had an <math>~n = \tfrac{3}{2}</math> polytropic equation of state, an n' = 0 angular momentum distribution, and an initial ratio of rotational to gravitational potential energy T/|W| = 0.30. As has been cataloged in Table 1, below, a YouTube animation carrying ID = BhRUqZe0Ly4 shows the nonlinear development of the bar-mode — actually, two-armed, spiral-mode — instability in Model A. The evolution is shown in the inertial reference frame and covers 46 dynamical times (20 central initial rotation periods) as defined by the properties of the initial, equilibrium axisymmetric model. Each frame of the Model A movie displays four nested isodensity contours at 80%, 40%, 4% and 0.4% of the maximum density. Via the trailing spiral structure, gravitational torques are able to effectively redistribute angular momentum on a dynamical time scale; a relatively small amount of material is shed into an equatorial disk. (This disk material is not visible in the Model A movie because the disk material all has a mass density less than 0.4% of the maximum density.) Over time, the central object (containing most of the initial object's mass) settles down into a new quasi-equilibrium configuration. The six images displayed in the upper portion of color figure shown here, on the right, have been extracted from this animation at six different points in time (measured in terms of the central initial rotation period), as labeled.
For comparison, we also have studied the development of the same type of bar-mode (two-armed, spiral) instability in a model which will be referred to here as Model B. It had an <math>~n = \tfrac{3}{2}</math> polytropic equation of state and an initial ratio of rotational to gravitational potential energy T/|W| = 0.28, but with an angular momentum distribution specified to produce a uniform vortensity profile in the initial model. (Vortensity is defined as the ratio of vorticity to mass density.) A YouTube animation carrying ID = Qh-bMto2e3k shows this evolution from an inertial frame and covers approximately 32 dynamical times as defined by the mean density of the initial model. The instability in this model has less of a pronounced spiral character, but ultimately results in the formation of a new triaxial, quasi-equilibrium configuration with properties that are similar to the end state of the Model A evolution.
As illustrated and discussed elsewhere, we are convinced that the ellipsoidal-like configurations that have been formed through both of these model simulations are compressible analogs of Riemann S-type ellipsoids.
| Table 1: Accompanying YouTube Animations (click on ID) | |||
| Model: | A | B | |
| Nonlinear Development of Bar-mode Instability (isodensity surfaces): | BhRUqZe0Ly4 | Qh-bMto2e3k | |
| Quasi-Steady-State "CARE" | Isodensity Surfaces: | z3RDthHnY3A | Eyl81O9s62s |
| Equatorial-Plane Fluid Flow: | fgjjzu3Nmo8 | yggbz9z8JQ4 | |
| Andalib's Analogous Prograde Flow-Field: | p550IDP8h-s | ||
| Meridional Fluid Flow: | _nXKv0k0h-Q | n/a | |
| Cooling Evolution | Isodensity Surfaces: | erYWHgaKYyc | n/a |
| Equatorial-Plane Fluid Flow: | nC4adQzlXrI | n/a | |
| Andalib's Analogous Binary Flow-Field: | nkwRJh2tgos | n/a | |
| Meridional Fluid Flow: | S0tg2jURzGE | n/a | |
Index of Relevant Publications
Here is a list of relevant research papers as largely enumerated by Y. Kojima & M. Saijo (2008) …
- [TDM85] J. E. Tohline, R. H. Durisen & M. McCollough (1985), ApJ, 298, 220: The linear and nonlinear dynamic stability of rotating N = 3/2 polytropes
|
HYDROCODE: Newtonian, 3D Eulerian, 1st-order donor-cell on a cylindrical grid; π-symmetry plus reflection symmetry through equatorial plane; <math>~\Gamma=5/3</math>; Poisson solved with FFT + Buneman cyclic reduction MODEL(s): Constructed using Ostriker-Mark SCF method; axisymmetric, n = 3/2 polytrope; n' = 0 rotation law; four different equilibrium configurations having T/|W| = 0.28, 0.30, 0.33, 0.35. |
- [DGTB86] R. H. Durisen, R. A. Gingold, J. E. Tohline & A. P. Boss (1986), ApJ, 305, 281: Dynamic Fission Instabilities in Rapidly Rotating N = 3/2 Polytropes: A Comparison of Results from Finite-Difference and Smoothed Particle Hydrodynamics Codes
- [WT87] H. A. Williams & J. E. Tohline (1987), ApJ, 315, 594: Linear and Nonlinear Dynamic Instability of Rotating Polytropes
|
HYDROCODE: Same as in Tohline, Durisen & McCollough (1985), above. MODEL(s): Constructed using Ostriker-Mark SCF method; axisymmetric, n' = 0 rotation law; five different equilibrium configurations having (see column 1 of their Table 1) n = 0.8, 1.0, 1.3, 1.5, 1.8, all having T/|W| = 0.310. |
- [WT88] H. A. Williams & J. E. Tohline (1988), ApJ, 334, 449: Circumstellar Ring Formation in Rapidly Rotating Protostars
|
Two of the models that were studied in Williams & Tohline (1987) — specifically, the models having n = 0.8 and 1.8 —
… are shown as they evolve to extremely nonlinear amplitudes: the end result in both cases is … The models shed a fraction of their mass and angular momentum, producing a ring which surrounds a more centrally condensed object … The central object is a triaxial figure that is rotating about its shortest axis.
|
- [HCS94] J. L. Houser, J. M. Centrella & S. C. Smith (1994), PRL, 72, 1314: Gravitational radiation from nonaxisymmetric instability in a rotating star
|
Using Newtonian dynamics and Newtonian gravity … we have carried out computer simulations of a differentially rotating compact star with a polytropic equation of state undergoing the dynamical bar instability. This instability has previously been modeled numerically by Tohline and collaborators in the context of star formation … Our work is the first to calculate [using a post-Newtonian approximation] the gravitational radiation produced by this instability, including wave forms and luminosities. It is also a significant advance over the earlier studies because, in addition to using better numerical techniques, we model the fluid correctly using an energy equation. This is essential due to the generation of entropy by shocks during the later stages of the evolution.
HYDROCODE: Newtonian, 3D Lagrangian-Cartesian (SPH as implemented by Hernquist & Katz 1989), Includes energy equation and does not impose π-symmetry; <math>~\Gamma=5/3</math>; Poisson solved with TREESPH MODEL(s): Constructed using the SCF method of Smith & Centrella (1992; see article #15 in R. d'Inverno), which is based on earlier work of Ostriker-Mark 1968 and Hachisu 1986; axisymmetric, n = 3/2 polytrope; n' = 0 rotation law; only one equilibrium configuration, with T/|W| = 0.30. |
- [SHC95] S. C. Smith, J. L. Houser & J. M. Centrella (1995), ApJ, 458, 236: Simulations of Nonaxisymmetric Instability in a Rotating Star: A Comparison between Eulerian and Smooth Particle Hydrodynamics
- [HC96] J. L. Houser & J. M. Centrella (1996), Phys. Rev. D, 54, 7278: Gravitational radiation from rotational instabilites in compact stellar cores with stiff equations of state
|
Extending the work of Houser, Centrella & Smith (1994) just mentioned — and closely paralleling the work of Williams & Tohline (1987, 1988) — they examine the development of the dynamical bar instability in configurations that have a range of different equations of state. HYDROCODE: Same as Houser, Centrella & Smith (1994) MODEL(s): Axisymmetric, n' = 0 rotation law; a total of 3 models examined with, respectively, (n, T/|W|) = (0.5, 0.31), (1.0, 0.32), (1.5, 0.32) — see their Table II. The SCF-based method used to construct these models and the (rather contrived) method used to map the continuum distribution of mass into the Lagrangian-based SPH code is discussed in detail in §III of the paper. |
Break 1
- [TIPD98] J. Toman, J. N. Imamura, B. J. Pickett & R. H. Durisen (1998), ApJ, 497, 370: Nonaxisymmetric Dynamic Instabilities of Rotating Polytropes. I. The Kelvin Modes
| Equilibrium Models constucted and examined by |
||||
|---|---|---|---|---|
| <math>~n</math> | <math>~n'</math> | <math>~T/|W|</math> | <math>~\Omega_p/\Omega_\mathrm{eq}</math> | <math>~R_p/R_\mathrm{eq}</math> |
| <math>~\tfrac{5}{4}</math> | 0 | 0.274 | 2.44 | 0.258 |
| 0.279 | 2.45 | 0.250 | ||
| 0.288 | 2.49 | 0.234 | ||
| 0.319 | 2.65 | 0.187 | ||
| 0.346 | 2.88 | 0.147 | ||
| 0.363 | 3.11 | 0.123 | ||
| <math>~\tfrac{3}{2}</math> | 0.266 | 2.97 | 0.258 | |
| 0.280 | 3.03 | 0.234 | ||
| 0.290 | 3.09 | 0.218 | ||
| 0.300 | 3.16 | 0.202 | ||
| 0.316 | 3.28 | 0.179 | ||
| 0.327 | 3.35 | 0.163 | ||
| 0.344 | 3.61 | 0.139 | ||
| 0.368 | 4.04 | 0.107 | ||
| 0.396 | 4.79 | 0.0754 | ||
| 1 | 0.262 | 6.85 | 0.139 | |
| 0.283 | 8.90 | 0.107 | ||
| 0.292 | 9.81 | 0.0958 | ||
| 0.311 | 12.4 | 0.0754 | ||
| <math>~\tfrac{3}{2}</math> | 0.272 | 15.1 | 0.0754 | |
| 0.280 | 16.9 | 0.0675 | ||
| 0.290 | 19.0 | 0.0595 | ||
| <math>~\tfrac{5}{2}</math> | 0 | 0.262 | 7.19 | 0.202 |
| 0.268 | 7.26 | 0.194 | ||
| 0.273 | 7.34 | 0.187 | ||
| 0.285 | 7.52 | 0.171 | ||
| 0.297 | 7.73 | 0.155 | ||
| 0.304 | 7.85 | 0.147 | ||
| 0.324 | 8.29 | 0.123 | ||
| 0.338 | 8.68 | 0.107 | ||
| 0.371 | 9.85 | 0.0754 | ||
| 0.389 | 10.8 | 0.0595 | ||
Break 2
- K. C. B. New, J. M. Centrella & J. E. Tohline (2000), Phys. Rev. D, 62, 064019: Gravitational waves from long-duration simulations of the dynamical bar instability
- M. Shibata, T. W. Baumgarte & S. L. Shapiro (2000), ApJ, 542, 453: The Bar-Mode Instability in Differentially Rotating Neutron Stars: Simulations in Full General Relativity
- Y.-T. Liu & L. Lindblom (2001), MNRAS, 324, 1063: Models of rapidly rotating neutron stars: remnants of accretion-induced collapse
- M. Saijo, M. Shibata, T. W. Baumgarte & S. L. Shapiro (2001), ApJ, 548, 919: Dynamical Bar Instability in Rotating Stars: Effect of General Relativity
- J. M. Centrella, K. C. B. New, L. L. Lowe & J. D. Brown (2001), ApJ, 550, L193: Dynamical Rotational Instability at Low T/W
- Y.-T. Liu (2002), Phys. Rev. D, 65, 124003: Dynamical instability of new-born neutron stars as sources of gravitational radiation
- M. Saijo, T. W. Baumgarte & S. L. Shapiro (2003), ApJ, 595, 352: One-armed Spiral Instability in Differentially Rotating Stars
- S. Ou & J. E. Tohline (2006), ApJ, 651, 1068: Unexpected Dynamical Instabilities in Differentially Rotating Neutron Stars
- L. Baiotti, R. De Pietri, G. M. Manco & L. Rezzolla (2007), Phys. Rev. D, 75, 044023: Accurate simulations of the dynamical bar-mode instability in full general relativity
- P. Cerda-Duran, V. Quilos & J. A. Font (2007), Comp. Phys. Comm., 177, 288: AMR simulations of the low T/|W| bar-mode instability of neutron stars
- S. Ou, J. E. Tohline & P. M. Motl (2007), ApJ, 665, 1074: Further Evidence for an Elliptical Instability in Rotating Fluid Bars and Ellipsoidal Stars
- M. Saijo & Y. Kojima (2008), Phys. Rev. D, 77, 063002: Faraday resonance in dynamical bar instability of differentially rotating stars
- Y. Kojima & M. Saijo (2008), Phys. Rev. D, vol. 78, Issue 12, id. 124001: Amplification of azimuthal modes with odd wave numbers during dynamical bar-mode growth in rotating stars
|
Nonlinear growth of the bar-mode deformation is studied for a differentially rotating star with supercritical rotational energy. In particular, the growth mechanism of some azimuthal modes with odd wave numbers is examined … Mode coupling to even modes, i.e., the bar mode and higher harmonics, significantly enhances the amplitudes of odd modes …
HYDROCODE: Newtonian, 3D Eulerian, Cartesian, with entropy tracer; reflection symmetry through equatorial plane; <math>~\Gamma=2</math>; Poisson solved with preconditioned conjugate gradient (PCG) method MODEL(s): axisymmetric, n = 1 polytrope; j-constant rotation law with A = 1; their Table I lists four different equilibrium configurations having T/|W| = 0.256, 0.268, 0.277, 0.281. |
Additional references identified through the above set of references:
- M. Saijo (2018), Phys. Rev. D, 98, 024003: Determining the stiffness of the equation of state using low T/W dynamical instabilities in differentially rotating stars
|
We investigate the nature of low T/W dynamical instabilities in various ranges of the stiffness of the equation of state in differentially rotating stars … We analyze these instabilities in both a linear perturbation analysis and a three-dimensional hydrodynamical simulation … the nature of the eigenfunction that oscillates between corotation and the surface for an unstable star requires reinterpretation of pulsation modes in differentially rotating stars. |
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |