User:Tohline/Appendix/Ramblings/RiemannB74C692

Another S-type Example b74c692

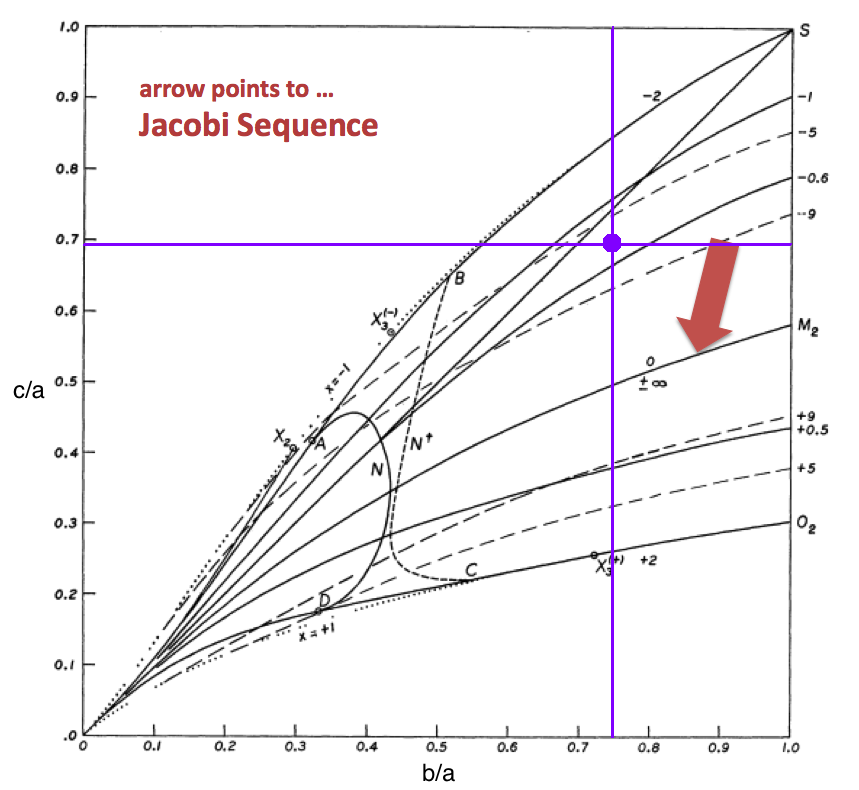
This chapter is an extension of the chapter we have titled, "Riemann Meets COLLADA & Oculus Rift S." In that chapter we used as our first example of a Riemann S-type ellipsoid the model with parameters, (b/a, c/a) = (0.41, 0.385). Here we construct a model with parameters, (b/a, c/a) = (0.74, 0.692). Other closely related chapters are listed below under the heading, "See Also".

Key Physical Parameters

The model that we have chosen to use in our second successful construction of a COLLADA-based, 3D and interactive animation has the following properties; this model has been selected from Table 2 of our accompanying discussion of Riemann S-type ellipsoids:

Figure 1a		<math>~\frac{b}{a} = 0.74</math>				Figure 1b
		<math>~\frac{c}{a} = 0.692</math>
		Direct		Adjoint
		<math>~\Omega_\mathrm{EFE} = 0.638747</math>		<math>~\Omega_\mathrm{EFE} = - 0.217773</math>
		<math>~\lambda_\mathrm{EFE} = 0.217773</math>		<math>~\lambda_\mathrm{EFE} = - 0.638747 </math>

The subscript "EFE" on Ω and λ means that the relevant frequency is given in units that have been adopted in [EFE], that is, in units of <math>~[\pi G\rho]^{1 / 2}</math>. In Figure 1a, the solid purple circular marker (where the pair of purple lines cross) identifies the location of this model in the "c/a versus b/a" diagram that appears as Figure 2 on p. 902 of S. Chandrasekhar (1965); essentially the same diagram appears in §49 (p. 147) of [EFE].

Coding Steps

Here we begin with a working model of b41c385 and use incremental changes in the COLLADA-based code to construct a working model of b74c692.

• Pulling from the earlier modeling subsection titled, Final Touches …
  • Final17.dae   TERRIFIC  !:
    Both hands of the clock now continue to cycle smoothly (through 9.126 "hours" = 9^h 8^m) while the laboratory frame completes 5.0 full spin periods — which will be 5.0 full spins of the ellipsoid as viewed from the inertial frame. This works in both visualization venues.
  • Inertial17.dae:
    This is identical to "Final17.dae" except that the system is viewed from the inertial frame of reference. This works in both visualization venues.
  • [KEEP] Inertial21.dae:
    Here, we set the "nudging" angle of the MidPlane to 0°, but moved the "nudging" angle of the ellipsoid from 0° to just 1°. This appears to work in both visualization venues.
• Pulling from a different earlier subsection titled, Multiple Lagrangian Fluid Elements …
  • MultiLagrange23.dae --> TestMulti23.dae:
    This model shows the motion of nine (small, red cube) Lagrange particles whose motion is confined to the equatorial plane of the Riemann ellipsoid. This nicely illustrates that the volume occupied by a region of fluid remains unchanged as the fluid moves around the ellipsoid.   This works in both visualization venues!
  • [KEEP] MultiLagrange26.dae:
    Here, we set the "nudging" angle of the MidPlane to 1°, and moved the "nudging" angle of the ellipsoid from 5° to 0°. Also, we bumped the purple's opacity up from 0.6 to 0.8. This appears to work in both visualization venues.
• TestMulti52.dae
  Same as MultiLagrange23.dae --> TestMulti23.dae, except the starting ellipsoid angle is nudged by 45° instead of 5°.
• [KEEP] TestMulti56.dae:
  Same as MultiLagrange26.dae, except we have attempted to replace the alpha-numeric labeling. SUCCESS! Works in all three visualization venues: Mac "Preview", PC "3D Viewer", and Oculus RIft S.
• Facebook glTF Transmutator (v1.5)
  I am only now appreciating that, when a ".glb"-formatted file is imported into the Oculus Rift S inventory, the importation step is handled by Facebook's glTF Transmutator (v1.5).
• TestMulti70b.dae
  Same as TestMulti56.dae, except we have inserted the correct EllipsoidOctant geometries (drawn from b74c692 Old_DRot.dae). This works in both visualization venues.
• TestMulti71.dae
  Incorporated proper tracking of nine Lagrangian fluid elements, drawn from b74c692 Old_DI.dae, but reexplained in the subsection below titled, location_X. This works in both visualization venues.
• TestMulti72.dae
  Incorporated (small yellow) markers that identify the orbit of a Lagrangian fluid element that lies in the equatorial plane and at the surface of the ellipsoid. The x and y coordinate values are tabulated in the subsection below titled, location_X. This works in both visualization venues. The fluid elements should be able to complete more than one orbit during the time that the ellipsoid spins 5 times; only one fluid orbit is included in this particular model.
• TestMulti73.dae
  Successfully registered the movement of the hands on the wall-clock. This works in both visualization venues. Now, decide whether or not to extend the orbital motion of the nine Lagrangian fluid elements beyond one orbit.

Quantitative Animation

rotation_euler_Z

Whether the observer is viewing the system from an inertial frame of reference or a rotating frame of reference, this animation section specifies the rate at which the ellipsoid spins and the rate at which the "laboratory" is spinning. Three sets of data must be specified:

1. The "First_rotation_euler_Z-input-array", which specifies TIME.
2. The "First_rotation_euler_Z-output-array", which specifies how the ANGLE of orientation of the ellipsoid varies with TIME.
3. The "Frame_rotation_euler_Z-output-array", which specifies how the spin ANGLE of the laboratory frame varies with TIME.

We have chosen to specify the time-varying angle in increments of 60° and to end the animation sequence after the ellipsoid (or, alternatively, the laboratory frame) has completed exactly five full spins. As a result — ignoring any zero-point offsets — one of the ANGLE arrays will vary from 0° to 5 × 360° = 1800° in 60° intervals (if spinning counter-clock-wise) or will vary from 1800° to 0° in -60° intervals (if spinning clock-wise). Again ignoring any zero-point offset, all the data values in the other ANGLE array will be 0°. The number of discrete data values that must be specified for each of the three arrays is therefore, by choice, count = (1800/60)+1 = 31.

All we have left to do is specify the TIME interval that is equivalent to a 60° turn of the ellipsoid, as viewed from the inertial frame of reference. Given that one cycle of the wall-clock's "minute" hand represents a frequency of <math>~[\pi G \rho]^{1 / 2}</math> and, furthermore by choice, we equate one cycle of the wall-clock's "minute" hand to TIME = 4 in COLLADA time units (approximately 4 seconds of real time), we know that one complete spin of the ellipsoid is equivalent to 4/|Ω_EFE| units of TIME. Hence the ellipsoid will turn through 60° in a time, ΔT_Ω = 4/[6|Ω_EFE|] and it will take TIME = 20/|Ω_EFE| to complete five full spins.

Direct
Model	ΩEFE	ΔTΩ	5 Spins
b41c385	0.547874	1.2168	36.505
b74c692	0.638747	1.0437	31.311
b90c333	0.447158	1.4909	44.727
b28c256	0.456676	1.4598	43.795

location_X

Here we illustrate the motion of one Lagrangian fluid element as it moves along an elliptical path (b/a aspect ratio) in the equatorial plane of the Riemann ellipsoid. First we acknowledge that every fluid element completes one full orbit in a COLLADA-based time of, TIME_λ = 4/|λ_EFE|. Dividing the orbit into 50 equally spaced intervals of time therefore specifies a time increment, ΔT_λ = 4/(50 |λ_EFE|). Drawing from a related accompanying discussion, we recognize that at each of these points in time — that is, for n = 1 → 50 — the x and y coordinate locations of the fluid element are given by the expressions,

<math>~x_n</math>	<math>~= </math>	<math>~\cos\biggl[-2\pi (n-1)\frac{\Delta T_\lambda}{4} \cdot \lambda_\mathrm{EFE}\biggr]</math>	and	<math>~y_n</math>	<math>~= </math>	<math>~\biggl(\frac{b}{a}\biggr)\sin\biggl[- 2\pi (n-1)\frac{\Delta T_\lambda}{4} \cdot \lambda_\mathrm{EFE} \biggr] </math>
	<math>~= </math>	<math>~\cos\biggl[-\frac{2\pi (n-1)}{50} \cdot \frac{\lambda_\mathrm{EFE}}{|\lambda_\mathrm{EFE}|} \biggr]</math>			<math>~= </math>	<math>~\biggl(\frac{b}{a}\biggr)\sin\biggl[ -\frac{2\pi (n-1)}{50} \cdot \frac{\lambda_\mathrm{EFE}}{|\lambda_\mathrm{EFE}|} \biggr] </math>

where we have assumed that the length of the longest axis of the ellipsoid is, a = 1. Note that, in the argument of these trigonometric functions, the sign of the frequency, λ_EFE, determines whether the fluid motion is regrograde (λ_EFE intrinsically positive) or prograde (λ_EFE intrinsically negative).

Direct
Model	λEFE	ΔTλ	1 Orbit	Frequency Ratio 5 × |λEFE/ΩEFE|	Count
b41c385	0.079886	1.0014	50.071	0.7291	37
b74c692	0.217773	0.3674	18.368	1.7046	86
b90c333	-0.221411	0.3613	18.066	2.4758	124
b28c256	0.020692	3.8662	193.31	0.2266	12

Here are some x-y coordinate pairs for a couple of model examples:

Direct
n	Axisymmetric		b41c385	b74c692
	x0	y0	y = 0.41 × y0	y = 0.74 × y0
1	1.0000	0.0000	0.0000	0.0000
2	0.9921	-0.1253	-0.0514	-0.0927
3	0.9686	-0.2487	-0.1020	-0.1840
4	0.9298	-0.3681	-0.1509	-0.2724
5	0.8763	-0.4818	-0.1975	-0.3565
6	0.8090	-0.5878	-0.2410	-0.4350
7	0.7290	-0.6845	-0.2807	-0.5066
8	0.6374	-0.7705	-0.3159	-0.5702
9	0.5358	-0.8443	-0.3462	-0.6248
10	0.4258	-0.9048	-0.3710	-0.6696
11	0.3090	-0.9511	-0.3899	-0.7038
12	0.1874	-0.9823	-0.4027	-0.7269
13	-0.9980	0.0628	-0.4092	-0.7385

How many complete (and fractional) orbits does each Lagrangian fluid element complete in the time it takes the ellipsoid to complete five spin periods? And, as a result, how many discrete steps in time does it traverse, assuming that each orbit has been dissected into 50 pieces? The answer to the first question is given by dividing "5 Spins" by "1 Orbit"; in the table above, we label this quantity as, "Frequency Ratio," given that it is equivalent to |5 × λ_EFE/Ω_EFE|. And the answer to the second question is,

Count

=

(50 × Frequency_Ratio) + 1 .

Cube_quaternion

Here we construct the wall-clock. First we recognize that the time required for the ellipsoid to complete "5 spins" is, as calculated above, TIME = 20/|Ω_EFE|. We have also dictated that the "minute hand" on the clock will complete one full cycle — that is, it will spin through an angle that starts at 0° and runs to γ = 360° — every 4 TIME units. While watching the ellipsoid spin five times, the "minute hand" must complete M = 5/|Ω_EFE| cycles.

We have chosen to model the motion of the "minute hand" by breaking each cycle (360°) into 16 equal divisions, that is, we have chosen to set Δγ = 360°/16 = 22.5°. This also means that the number of discrete time values will be INT(M × 16) + 1 = INT(80/|Ω_EFE|) + 1.

To be used in the Quaternion Array γ (degrees) sin γ cos γ -90.0 -1.0000 0.0000 -112.5 -0.9239 -0.3827 -135.0 -0.7071 -0.7071 -157.5 -0.3827 -0.9239 -180.0 0.0000 -1.0000 -202.5 0.3827 -0.9239 -225.0 0.7071 -0.7071 -247.5 0.9239 -0.3827 -270.0 1.0000 0.0000 -292.5 0.9239 0.3827 -315.0 0.7071 0.7071 -337.5 0.3827 0.9239 0.0 0.0000 1.0000 -22.5 -0.3827 0.9239 -45.0 -0.7071 0.7071 -67.5 -0.9239 0.3827

Clock Model "Minute Hand" Cycles Discrete Steps N/A b41c385 9.1261 147 --- b74c692 7.8278 126 --- b90c333 11.1817 179 --- b28c256 10.9487 176

As we have detailed in a parallel discussion, at each discrete time step, the equivalent <matrix> instruction should be of the form,

<matrix>[ 0 ]   [ 0 ]   [ -Sx ]   [ Tx ]     [ Sy · sin(γ) ]   [ Sy · cos(γ) ]   [ 0 ]   [ Ty ]     [ Sz · cos(γ) ]   [ -Sz · sin(γ) ]   [ 0]   [ Tz ]     [ 0 ]   [ 0 ]   [ 0 ]   [ 1 ]</matrix> .

COLLADA Model Files

b74c692DI.dae [Direct Inertial Frame]    …     a COLLADA code containing nnnn lines of <xml>-formatted ASCII text

<?xml version="1.0" encoding="UTF-8" standalone="no" ?>

b74c692DRot.dae [Direct Rotating Frame]    …     a COLLADA code containing nnnn lines of <xml>-formatted ASCII text

<?xml version="1.0" encoding="UTF-8" standalone="no" ?>

b74c692AI.dae [Adjunct Inertial Frame]    …     a COLLADA code containing nnnn lines of <xml>-formatted ASCII text

<?xml version="1.0" encoding="UTF-8" standalone="no" ?>

b74c692ARot.dae [Adjunct Rotating Frame]    …     a COLLADA code containing nnnn lines of <xml>-formatted ASCII text

<?xml version="1.0" encoding="UTF-8" standalone="no" ?>

See Also

• Discussion of Ou's Riemann-Like Ellipsoids

• Riemann Meets COLLADA & Oculus Rift S
  • Virtual Reality and 3D Printing
  • Success Importing Animated Scene into Oculus Rift S
  • Carefully (Re)Build Riemann Type S Ellipsoids Inside Oculus Rift Environment: Example (b/a, c/a) = (0.41, 0.385)
  • Other Example S-type Riemann Ellipsoids:
    • (b/a, c/a) = (0.90, 0.333)
    • (b/a, c/a) = (0.74, 0.692)
    • (b/a, c/a) = (0.28, 0.256)

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation