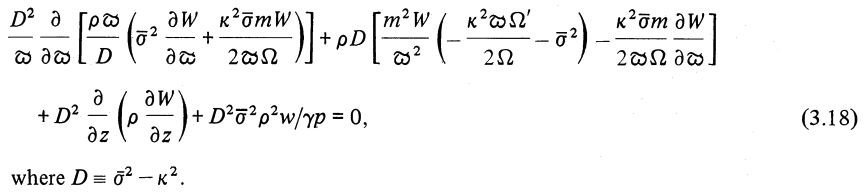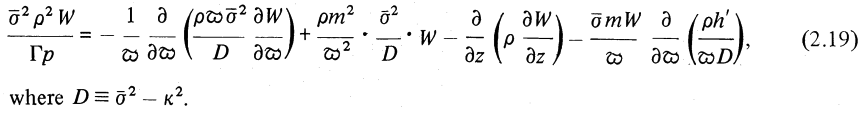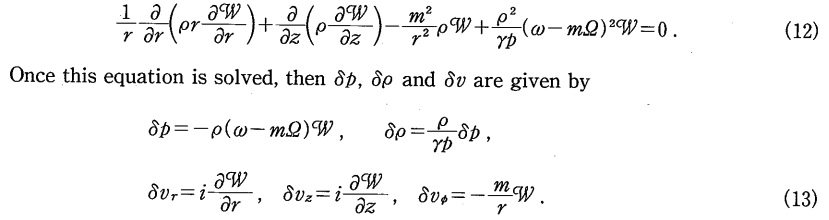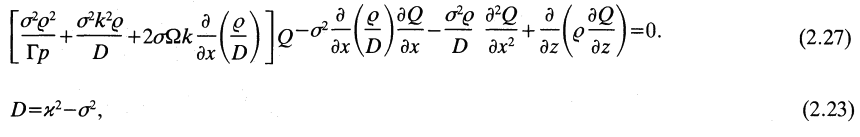User:Tohline/Apps/PapaloizouPringle84
Nonaxisymmetric Instability in Papaloizou-Pringle Tori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Linearized Principal Governing Equations in Cylindrical Coordinates
We begin by drawing from an accompanying derivation the relevant set of linearized principal governing equations, written in cylindrical coordinates but, following the lead of Papaloizou & Pringle (1984, MNRAS, 208, 721-750; hereafter, PP84), express each perturbation in the form,
|
<math>~q^'~~\rightarrow~~ q^' (\varpi,z) f_\sigma</math> |
where, |
<math>~f_\sigma \equiv e^{i(m\varphi + \sigma t)} \, ,</math> |
and, set <math>~\Phi^' = 0</math> — hence, the Poisson equation becomes irrelevant — because the torus is assumed not to be self-gravitating and the background (point source) potential, <math>~\Phi_0</math>, is assumed to be unchanging.
|
Set of Linearized Principal Governing Equations in Cylindrical Coordinates |
||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||
Next, taking derivatives of <math>~f_\sigma</math>, where indicated, then dividing every equation through by <math>~f_\sigma</math> gives,
| Linearized Adiabatic Form of the 1st Law of Thermodynamics | ||
|
<math>~\frac{P^' }{P_0}</math> |
<math>~=</math> |
<math>~ \frac{\gamma \rho^' }{\rho_0} \, ;</math> |
| Linearized <math>\varpi</math> Component of Euler Equation | ||
|
<math>~{\dot\varpi}^'[i(\sigma + m{\dot\varphi}_0)] - 2 {\dot\varphi}_0 (\varpi {\dot\varphi}^' ) </math> |
<math>~=</math> |
<math>~ - \frac{\partial}{\partial\varpi}\biggl( \frac{P^'}{\rho_0} \biggr) \, ; </math> |
| Linearized <math>\varphi</math> Component of Euler Equation | ||
|
<math>~(\varpi {\dot\varphi}^')[i(\sigma + m{\dot\varphi}_0)] + \frac{{\dot\varpi}^'}{\varpi}\biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] </math> |
<math>~=</math> |
<math>~- \frac{ im}{\varpi} \biggl(\frac{P^'}{\rho_0}\biggr) \, ; </math> |
| Linearized <math>~z</math> Component of Euler Equation | ||
|
<math>~ ~{\dot{z}}^'[i(\sigma + m{\dot\varphi}_0)] </math> |
<math>~=</math> |
<math>~ - \frac{\partial}{\partial z}\biggl( \frac{P^'}{\rho_0} \biggr) \, ; </math> |
| Linearized Continuity Equation | ||
|
<math>~\rho^'[i(\sigma + m{\dot\varphi}_0)] + i m\rho_0 {\dot\varphi}^' </math> |
<math>~=</math> |
<math>~ - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi {\dot\varpi}^' \biggr] - \frac{\partial}{\partial z} \biggl[ \rho_0 {\dot{z}}^' \biggr] \, . </math> |
These five equations match, respectively, equations (3.8) - (3.12) of PP84.
Rewritten Velocity Components
PP84
Again following the lead of PP84, we let <math>~W^'</math> represent the (normalized) perturbation in the fluid entropy, specifically,
|
<math>~W^' </math> |
<math>~\equiv</math> |
<math>~\frac{P^'}{\rho_0(\sigma + m{\dot\varphi}_0)} </math> |
|
<math>~\Rightarrow~~~~\frac{\partial}{\partial\varpi}\biggl(\frac{P^'}{\rho_0} \biggr)</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial\varpi} \biggl[ W^'(\sigma + m{\dot\varphi}_0 )\biggr]</math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0 )\frac{\partial W^'}{\partial\varpi} + mW^'\frac{\partial {\dot\varphi}_0 }{\partial\varpi} </math> |
in which case the three linearized components of the Euler equation may be rewritten as,
| Linearized <math>\varpi</math> Component of Euler Equation | ||
|
<math>~{\dot\varpi}^' </math> |
<math>~=</math> |
<math>~ i \biggl[ \frac{\partial W^'}{\partial\varpi} + \frac{mW^'}{(\sigma + m{\dot\varphi}_0)}\frac{\partial {\dot\varphi}_0 }{\partial\varpi} - \frac{2{\dot\varphi}_0 (\varpi {\dot\varphi}^' )}{(\sigma + m{\dot\varphi}_0)} \biggr] </math> |
| Linearized <math>\varphi</math> Component of Euler Equation | ||
|
<math>~(\varpi {\dot\varphi}^') </math> |
<math>~=</math> |
<math>~- \frac{ mW^'}{\varpi} + i~ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] \, ; </math> |
| Linearized <math>~z</math> Component of Euler Equation | ||
|
<math>~ ~{\dot{z}}^' </math> |
<math>~=</math> |
<math>~ i~\frac{\partial W^'}{\partial z} \, . </math> |
Using the second of these three relations to provide an expression for <math>~(\varpi {\dot\varphi}^')</math> in terms of <math>~W^'</math> and <math>~{\dot\varpi}^'</math>, and plugging this expression into the first relation allows us to solve for the radial component of the perturbed velocity in terms of <math>~W^'</math> and its radial derivative. Specifically, we obtain,
|
<math>~{\dot\varpi}^' </math> |
<math>~=</math> |
<math>~i \frac{\partial W^'}{\partial \varpi} + i~\frac{mW^'}{(\sigma + m{\dot\varphi}_0)} \biggl[ \frac{\kappa^2}{2\varpi {\dot\varphi}_0} - \frac{2 {\dot\varphi}_0 }{\varpi}\biggr] - i~ \frac{2 {\dot\varphi}_0 }{(\sigma + m{\dot\varphi}_0)} \biggl[ - \frac{ mW^'}{\varpi} + i~ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl( \frac{ \kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~i \frac{\partial W^'}{\partial \varpi} + i~\frac{mW^'}{(\sigma + m{\dot\varphi}_0)} \biggl[ \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr] + \biggl[ \frac{2 {\dot\varphi}_0 }{(\sigma + m{\dot\varphi}_0)} \biggr]\biggl[ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl( \frac{ \kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~i \biggl[ \frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) \frac{ mW^'}{\bar\sigma} \biggr] + \biggl[ {\dot\varpi}^'\biggl( \frac{ \kappa^2 }{ {\bar\sigma}^2 } \biggr) \biggr] </math> |
|
<math>~\Rightarrow ~~~~ {\dot\varpi}^' ({\bar\sigma}^2 - \kappa^2 )</math> |
<math>~=</math> |
<math>~i \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) mW^' \bar\sigma \biggr] \, , </math> |
where, adopting notation from PP84,
|
<math>~\kappa^2 \equiv \frac{2{\dot\varphi}_0}{\varpi} \biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr]</math> |
and |
<math>~{\bar\sigma} \equiv (\sigma + m{\dot\varphi}_0) \, .</math> |
This means, as well, that,
|
<math>~(\varpi {\dot\varphi}^') ({\bar\sigma}^2 - \kappa^2 ) </math> |
<math>~=</math> |
<math>~- \frac{ mW^'}{\varpi} ({\bar\sigma}^2 - \kappa^2 ) - \frac{ 1 }{\varpi \bar\sigma }\biggl[ \frac{\kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr] \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{2 {\dot\varphi}_0}{\varpi} + \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) mW^' \bar\sigma \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ m{\bar\sigma}^2 W^'}{\varpi} + \frac{ m\kappa^2W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{2 {\dot\varphi}_0}{\varpi} + \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \, . </math> |
In summary, the three components of the perturbed velocity are:
|
Cylindrical-Coordinate Components of the Perturbed Velocity from PP84 |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
where, the square of the epicyclic frequency,
| |||||||||||||||||||||
These three velocity-component expressions match, respectively, equations (3.14), (3.15), and (3.16) of PP84.
GGN86
In §2.2 of their paper, P. Goldreich, J. Goodman, and R. Narayan (1986, MNRAS, 221, 339) — hereafter, GGN86 — also present expressions for the three components of the perturbed velocity. Here we seek to identify key differences in approach but, ultimately, highlight the degree of agreement between the GGN86 and the PP84 analyses.
Preamble
First, let's make the substitution,
<math>Q_{JT} \equiv (\sigma + m{\dot\varphi}_0) W^' \, ,</math>
in which case,
|
<math>~\frac{\partial W^'}{\partial\varpi}</math> |
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)^{-1} \frac{\partial Q_{JT} }{\partial \varpi} - Q_{JT} (\sigma + m{\dot\varphi}_0)^{-2} m\frac{\partial {\dot\varphi}_0}{\partial \varpi} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)^{-2} \biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \, . </math> |
Then we can rewrite the radial component of the perturbed velocity as,
|
<math>~i~ {\dot\varpi}^' ( \kappa^2 - {\bar\sigma}^2 )</math> |
<math>~=</math> |
<math>~\biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) m Q_{JT} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} +m Q_{JT} \biggl[ \biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) -\biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} +m Q_{JT} \biggl\{ \frac{1}{\varpi^2} \biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] -\biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} + (2\dot\varphi_0)\frac{m Q_{JT}}{\varpi} </math> |
|
<math>~{\dot\varpi}^' ( \kappa^2 - {\bar\sigma}^2 )</math> |
<math>~=</math> |
<math>~- i~\bar\sigma \frac{\partial Q_{JT} }{\partial \varpi} - (2i\dot\varphi_0)\frac{m Q_{JT}}{\varpi} \, . </math> |
Similarly, we can rewrite the azimuthal component of the perturbed velocity as,
|
<math>~(\varpi {\dot\varphi}^') ( \kappa^2 - {\bar\sigma}^2) </math> |
<math>~=</math> |
<math>~ \frac{ m{\bar\sigma}^2 }{\varpi}(\sigma + m{\dot\varphi}_0)^{-1}Q_{JT} + \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl\{ ~(\sigma + m{\dot\varphi}_0)^{-2} \biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi}
- m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{m}{\bar\sigma } (\sigma + m{\dot\varphi}_0)^{-1}Q_{JT} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ m{\bar\sigma} }{\varpi} Q_{JT} + \frac{\kappa^2 }{ 2{\dot\varphi}_0 } \biggl\{ ~\biggl[ \frac{\partial Q_{JT} }{\partial \varpi}
- \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \frac{m}{\bar\sigma} Q_{JT} \biggr] +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{m}{\bar\sigma } Q_{JT} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\kappa^2 }{ 2{\dot\varphi}_0 } \biggr) \frac{\partial Q_{JT} }{\partial \varpi} + \bar\sigma \frac{mQ_{JT} }{\varpi} \, . </math> |
Finally, the vertical component of the perturbed velocity becomes,
|
<math>~ ~{\dot{z}}^' </math> |
<math>~=</math> |
<math>~ i~(\sigma + m{\dot\varphi}_0)^{-1} \frac{\partial Q_{JT}}{\partial z} \, . </math> |
|
<math>~\Rightarrow~~~~i~\bar\sigma {\dot{z}}^' </math> |
<math>~=</math> |
<math>~ -\frac{\partial Q_{JT}}{\partial z} \, . </math> |
Nod to Oort Constants and Simple Rotation Profiles
Acknowledging the galactic dynamics community's familiarity with the so-called Oort constants, and in anticipation of our review of the GGN86 derivation that follows, we define the following two "Oort functions":
|
<math>~A</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, ,</math> |
|
<math>~B</math> |
<math>~\equiv</math> |
<math>~\frac{1}{2}\biggl[ {\dot\varphi}_0 + \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, .</math> |
Given these definitions, we note that,
|
<math>~B - A </math> |
<math>~=</math> |
<math>~{\dot\varphi}_0 \, ;</math> |
and, given the definition of the square of the epicyclic frequency, above, we can write,
|
<math>~\kappa^2</math> |
<math>~=</math> |
<math>~4{\dot\varphi}_0 B = 4B (B - A) \, .</math> |
In line with our own discussion of simple rotation profiles (but note that, in that chapter, the variable we use for the power-law exponent is different from theirs), GGN86 adopt a generalized power-law rotation profile of the form (see their equation 2.1),
|
<math>~{\dot\varphi}_0(\varpi)</math> |
<math>~=</math> |
<math>~ \Omega_0 \biggl( \frac{\varpi}{\varpi_0} \biggr)^{-q} \, ,</math> |
in which case we also have,
|
<math>~\frac{\partial}{\partial \varpi} \biggl( \varpi {\dot\varphi}_0 \biggr)</math> |
<math>~=</math> |
<math>~ \frac{\partial}{\partial \varpi} \biggl[ \Omega_0 \varpi_0^{q} \varpi^{1-q}\biggr] = (1-q){\dot\varphi}_0 \, .</math> |
Given this particular adopted profile, it is therefore clear that,
|
<math>~A_\mathrm{GGN}</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - (1-q) {\dot\varphi}_0\biggr] = - \frac{q}{2} {\dot\varphi}_0 \, ;</math> |
|
<math>~B_\mathrm{GGN}</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{2}\biggl[ {\dot\varphi}_0 + (1-q) {\dot\varphi}_0\biggr] = \frac{1}{2} (2-q) {\dot\varphi}_0 \, ;</math> |
|
<math>~\kappa^2_\mathrm{GGN}</math> |
<math>~=</math> |
<math>~4{\dot\varphi}_0 \biggl[ \frac{1}{2} (2-q) {\dot\varphi}_0 \biggr] = 2(2-q){\dot\varphi}_0^2 \, .</math> |
These three expressions are in line with GGN86 equations (2.4), (2.6), and (2.24), respectively.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Velocity Components
Direct Comparison of Derived Equations
The left panel of the following equation-table presents, once again, our above rewrite of the three components of the perturbed velocity derived in PP84 after we have replaced <math>~\kappa^2</math> (on the right-hand side of the <math>~\varphi</math> component) with its expression in terms of the "Oort function", <math>~B</math>. For comparison, the right panel of the same equation-table shows the analogous perturbed velocity-component expressions derived by GGN86 (see their equations 2.21 - 2.25).
|
Rewrite of the Components of the Perturbed Velocity from PP84 |
Perturbed Velocity Components from §2.2 of GGN86 |
||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||
These sets of expressions are identical if we adopt the following three variable mappings,
|
<math>~Q_{JT}\equiv\bar\sigma W^'</math> |
<math>~\leftrightarrow</math> |
<math>~Q \, ,</math> |
|
<math>~-~\bar\sigma </math> |
<math>~\leftrightarrow</math> |
<math>~\sigma_\mathrm{GGN} \, ,</math> |
|
<math>~m/\varpi</math> |
<math>~\leftrightarrow</math> |
<math>~k \, ,</math> |
and recognize that the appropriate association between the variable names that has been used for the three perturbed velocity-components is:
|
<math>~{\dot\varpi}^'</math> |
<math>~\leftrightarrow</math> |
<math>~u \, ,</math> |
|
<math>~(\varpi {\dot\varphi}^') </math> |
<math>~\leftrightarrow</math> |
<math>~v \, ,</math> |
|
<math>~{\dot{z}}^'</math> |
<math>~\leftrightarrow</math> |
<math>~w \, .</math> |
Checking Self-Consistency
|
<math>~A</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, ,</math> |
|
<math>~\Rightarrow~~~~ -2A</math> |
<math>~=</math> |
<math>~- \varpi \frac{\partial {\dot\varphi}_0}{\partial \varpi}</math> |
|
<math>~\Rightarrow~~~~ \frac{\partial {\dot\varphi}_0}{\partial \varpi}</math> |
<math>~=</math> |
<math>~\frac{2A}{\varpi}</math> |
Now, expand the function, <math>~{\dot\varphi}_0(\varpi)</math> in a Taylor series …
|
<math>~{\dot\varphi}_0(\varpi) </math> |
<math>~\approx</math> |
<math>~\Omega_0 + (\varpi - \varpi_0)\frac{\partial {\dot\varphi}_0}{\partial\varpi}\biggr|_{\varpi_0}</math> |
|
|
<math>~=</math> |
<math>~\Omega_0 + (\varpi - \varpi_0)\frac{2A}{\varpi_0}</math> |
|
<math>~\Rightarrow ~~~~\bar\sigma \equiv (\sigma + m{\dot\varphi}_0)</math> |
<math>~\approx</math> |
<math>~\sigma + \biggl[m\Omega_0 + \frac{2mA}{\varpi_0}(\varpi - \varpi_0)\biggr]</math> |
Now, from equations (2.18) and (2.15) of GGN86, along with their definition of the independent variable, <math>~x</math>, we have,
|
<math>~- \sigma_\mathrm{GGN}</math> |
<math>~=</math> |
<math>~- \omega_\mathrm{GGN} + 2Akx</math> |
|
|
<math>~=</math> |
<math>~- \omega_\mathrm{GGN} + \frac{2mA}{\varpi_0} (\varpi-\varpi_0) \, .</math> |
Hence, we can understand the desired mapping, <math>\bar\sigma \leftrightarrow - \sigma_\mathrm{GGN}</math>, if we acknowledge the more fundamental mapping,
<math>~\omega_\mathrm{GGN} ~~ \leftrightarrow ~~ - (\sigma+m\Omega_0) \, .</math>
Adopting Kojima's (1986) <math>~y_1</math> and <math>~y_2</math> notation, which we have discussed in a separate but closely related chapter, we therefore have,
|
<math>~y_1 </math> |
<math>~=</math> |
<math>~\frac{\mathrm{Re}(\omega_\mathrm{GGN})}{\Omega_0} - m </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{1}{\Omega_0} \biggr) \mathrm{Re}\biggl[ - (\sigma+m\Omega_0) \biggr] - m </math> |
|
<math>~y_2 </math> |
<math>~=</math> |
<math>~\frac{\mathrm{Im}(\omega_\mathrm{GGN})}{\Omega_0} \, ,</math> |
Formulation of Eigenvalue Problem
Seminal Work by Papaloizou & Pringle
Let's plug the three expressions for the components of the perturbed velocity into the linearized continuity equation and, as well, replace <math>~\rho^'</math> in favor of <math>~W^'</math> via the expression,
|
<math>~W^' </math> |
<math>~\equiv</math> |
<math>~\frac{P^'}{\rho_0(\sigma + m{\dot\varphi}_0)} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{ (\sigma + m{\dot\varphi}_0)} \biggl(\frac{\gamma P_0 \rho^' }{\rho_0^2}\biggr) \, .</math> |
Also multiplying through by <math>~-i</math>, we obtain,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\rho^'[(\sigma + m{\dot\varphi}_0)] + \frac{m\rho_0}{\varpi} (\varpi {\dot\varphi}^' ) - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi (i {\dot\varpi}^' ) \biggr] - \frac{\partial}{\partial z} \biggl[ \rho_0 (i{\dot{z}}^') \biggr] </math> |
|
|
<math>~=</math> |
<math>~{\bar\sigma}^2 \biggl( \frac{\rho_0^2 W^'}{\gamma P_0 } \biggr) + \frac{m\rho_0}{\varpi ({\bar\sigma}^2 - \kappa^2 )} \biggl\{ - \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{({\bar\sigma}^2 - \kappa^2 )} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) mW^' \bar\sigma \biggr] \biggr\} + \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} \, . </math> |
Multiplying through by <math>~D^2 \equiv ({\bar\sigma}^2 - \kappa^2)^2</math> and reorganizing terms gives,
|
<math>~0 </math> |
<math>~=</math> |
<math>~ \frac{D^2}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{D} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr] \biggr\} + \frac{D m\rho_0}{\varpi} \biggl\{ - \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \biggr\} </math> |
|
|
|
<math>~ + D^2 \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} + \biggl( \frac{D^2 {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{D^2}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{D} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr] \biggr\} + \rho_0 D \biggl\{ - \frac{m^2W^' }{\varpi^2 } \biggl[{\bar\sigma}^2 + \frac{\kappa^2 \varpi }{ 2 {\dot\varphi}_0 } \biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] - \frac{m\kappa^2 {\bar\sigma} }{ 2\varpi{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} \biggr]\biggr\} </math> |
|
|
|
<math>~ + D^2 \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} + \biggl( \frac{D^2 {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \biggr) \, . </math> |
As can be confirmed by comparing it to equation (3.18) of PP84 — which, to facilitate comparison, has been extracted and displayed in the following framed image — this expression matches the 2nd-order, two-dimensional PDE that defines the eigenvalue problem discussed by Papaloizou and Pringle in their seminal 1984 paper.
|
Equation (3.18) extracted without modification from p. 726 of Papaloizou & Pringle (1984)
"The dynamical stability of differentially rotating discs with constant specific angular momentum"
Monthly Notices of the Royal Astronomical Society, vol. 208, pp. 721-750 © Royal Astronomical Society |
After dividing through by <math>~D^2</math> and, again, rearranging terms, we also have,
|
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } </math> |
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{\frac{\rho_0 \varpi}{D} \biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr\} </math> |
|
|
|
<math>~ + \frac{\rho_0}{D} \biggl\{ \frac{m^2 {\bar\sigma}^2 W^' }{\varpi^2 } \biggr\} + \frac{\rho_0}{D} \biggl\{ \frac{m^2W^' }{\varpi^2 } \biggl[\frac{\kappa^2 \varpi }{ 2 {\dot\varphi}_0 } \biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] \biggr\} + \frac{\rho_0}{D} \biggl\{\frac{m\kappa^2 {\bar\sigma} }{ 2\varpi{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} \biggr]\biggr\} </math> |
|
|
|
<math>~ - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} + \biggl\{ \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} \biggr\} - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
|
<math>~ -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0 \kappa^2m }{2 {\dot\varphi}_0 D} \biggl( W^' \bar\sigma \biggr) \biggr] + \frac{\rho_0 \kappa^2 m}{2 {\dot\varphi}_0 D} \biggl[ \frac{W^' }{\varpi} \cdot \frac{\partial (m{\dot\varphi}_0)}{\partial\varpi} \biggr] + \frac{\kappa^2 m \rho_0}{2{\dot\varphi}_0 D} \biggl[\frac{ {\bar\sigma} }{\varpi} \cdot \frac{\partial W^'}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} + \biggl\{ \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} \biggr\} - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
|
<math>~ -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0 \kappa^2m }{2 {\dot\varphi}_0 D} ( W^' \bar\sigma ) \biggr] + \frac{\rho_0 \kappa^2 m}{2 {\dot\varphi}_0 D} \biggl[ \frac{1}{\varpi} \cdot \frac{\partial (W^' \bar\sigma)}{\partial\varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr) + \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{m W^' \bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \, . </math> |
Here, it is advantageous to note that, in place of the definition of the (square of the) epicyclic frequency provided above, we could have equally well written,
<math>~\kappa^2 = \frac{1}{\varpi^3} \frac{d j_0^2}{d \varpi} \, ,</math>
where, <math>~j_0(\varpi)\equiv \varpi^2{\dot\varphi}_0(\varpi)</math> is a function that specifies how the fluid's specific angular momentum varies with radius in the initial, unperturbed, equilibrium configuration. (See our related discussion of Simple Rotation Profiles.) From this relation, we recognize as well that,
|
<math>~\frac{dj_0}{d\varpi}</math> |
<math>~=</math> |
<math>~\frac{\kappa^2 \varpi^3}{2j_0} = \frac{\kappa^2 \varpi}{2{\dot\varphi}_0} \, .</math> |
So the last term inside the square brackets of our expression could meaningfully be written as,
|
<math>~\biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr]</math> |
<math>~~\rightarrow~~</math> |
<math>~\biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{dj_0}{d\varpi} \biggr)\biggr] \, .</math> |
If we let <math>~h^'</math> represent the radial derivative of the specific angular momentum in the initial, unperturbed, equilibrium configuration (Papaloizou & Pringle use "h" instead of "j" to denote the specific angular momentum, and they use a prime to denote differentiation with respect to the radial coordinate), we see that our derived expression matches equation (2.19) of Papaloizou & Pringle (1985) — which, to facilitate comparison, has been extracted and displayed in the following framed image. Clearly this mathematical definition of the eigenvalue problem discussed by PP85 is fundamentally the same as the one introduced and discussed in PP84.
|
Equation (2.19) extracted without modification from p. 803 of Papaloizou & Pringle (1985)
"The dynamical stability of differentially rotating discs. II"
Monthly Notices of the Royal Astronomical Society, vol. 213, pp. 799-820 © Royal Astronomical Society |
Analyses of Configurations with Uniform Specific Angular Momentum
Presumably PP85 rewrote the equation in the latest form presented above in order to help make it clear how the equation simplifies (specifically, the last term on the right-hand side vanishes) for configurations that initially have uniform specific angular momentum — that is, for configurations in which <math>~h^' = 0</math>. But other simplifications arise as well because the epicyclic frequency, <math>~\kappa</math>, also goes to zero in configurations with uniform specific angular momentum. This means that the frequency ratio, <math>~{\bar\sigma}^2/D</math>, that appears in two terms of our derived expression goes to unity, that is,
|
<math>~\frac{{\bar\sigma}^2}{D}\biggr|_{j_0-\mathrm{constant}} = \biggl[ \frac{{\bar\sigma}^2}{{\bar\sigma}^2 - \kappa^2}\biggr]_{j_0-\mathrm{constant}}</math> |
<math>~~\rightarrow~~</math> |
<math>~1 \, .</math> |
Implementing both of these simplifications, the latest form of our "eigenvalue problem" equation becomes,
|
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } </math> |
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \cancelto{1}{\biggl(\frac{{\bar\sigma}^2}{D} \biggr)} \rho_0 \varpi \cdot \frac{\partial W^'}{\partial \varpi} \biggr] + \cancelto{1}{\biggl(\frac{{\bar\sigma}^2}{D} \biggr)} \frac{\rho_0 m^2 W^' }{\varpi^2} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{m W^' \bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \cancelto{0}{\biggl( \frac{dj_0 }{d\varpi } \biggr)} \biggr] </math> |
|
<math>~\Rightarrow~~~~0 </math> |
<math>~=</math> |
<math>~ \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi \cdot \frac{\partial W^'}{\partial \varpi} \biggr] + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{\rho_0 m^2 W^' }{\varpi^2} + \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \, . </math> |
As can be confirmed by comparing it to equation (12) of Kojima (1986) — which, to facilitate comparison, has been extracted and displayed in the following framed image — this expression matches the 2nd-order, two-dimensional PDE that defines the eigenvalue problem discussed by Kojima.
|
Equations (12) & (13) extracted without modification from p. 254 of Kojima (1986)
"The Dynamical Stability of a Fat Disk with Constant Specific Angular Momentum"
Progress of Theoretical Physics, vol. 75, pp. 251-261 © Royal Astronomical Society |
|
Equation (1.6) extracted without modification from p. 555 of Blaes (1985)
"Oscillations of Slender Tori"
Monthly Notices of the Royal Astronomical Society, vol. 216, pp. 553-563 © Royal Astronomical Society |
Slender Torus Approximation
The discussion in this subsection builds on our above derivation of equation (3.18) in PP84 and equation (2.19) in PP85. Following along the lines of the variable substitution that was made earlier in our "preamble", let's replace <math>~W^'</math> with <math>~Q_{JT} \equiv \bar\sigma W^'</math> throughout this expression. As was also pointed out above, because <math>~\bar\sigma</math> is a function of the radial coordinate, we note that,
|
<math>~\frac{\partial \bar\sigma}{\partial\varpi}</math> |
<math>~=</math> |
<math>~ m \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \, , </math> |
and,
|
<math>~\frac{\partial W^'}{\partial\varpi}</math> |
<math>~=</math> |
<math>~{\bar\sigma}^{-2} \biggl[ {\bar\sigma} \frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \, . </math> |
Making these substitutions in equation (2.19) of PP85, we have,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 Q_{JT} }{\gamma P_0 \bar\sigma } + \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi }{D} \cdot \biggl[ {\bar\sigma} \frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr]\biggr\} - \frac{\rho_0 m^2 {\bar\sigma} Q_{JT} }{\varpi^2 D} + \frac{1}{\bar\sigma}\frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) + \frac{m Q_{JT} }{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \, . </math> |
Then, multiplying through by <math>~\bar\sigma</math> and rearranging terms, gives,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggl( \frac{ \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \biggr\}Q_{JT} ~ + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~ -~ \frac{m\bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi Q_{JT} }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} +~ \frac{\bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\bar\sigma \rho_0 \varpi }{D} \cdot \biggl[ \frac{\partial Q_{JT} }{\partial \varpi}\biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] \biggr\}Q_{JT} ~ + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~ -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \frac{\partial Q_{JT}}{\partial\varpi} -~ \frac{m\bar\sigma Q_{JT} }{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} +~ {\bar\sigma}^2 \biggl(\frac{\partial Q_{JT} }{\partial \varpi}\biggr) \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) +~ \frac{\bar\sigma}{\varpi}\frac{\rho_0 }{D} \cdot \frac{\partial Q_{JT} }{\partial \varpi} \biggl[\bar\sigma + m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] -~ \frac{\bar\sigma }{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \biggl(\frac{\rho_0 }{D}\biggr)m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \biggr\}Q_{JT} ~ </math> |
|
|
|
<math>~+ \biggl\{ -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) +~ {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) +~ \frac{\bar\sigma}{\varpi}\frac{\rho_0 }{D} \biggl[\bar\sigma + m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] \biggr\}\frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] \biggr\}Q_{JT} ~ + {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl\{ \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 \biggr] +\frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ \varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \biggl[ \varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] -~ \frac{\partial}{\partial\varpi} \biggl[ \biggl(\frac{\rho_0 }{D}\biggr)\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \biggr\}Q_{JT} ~ </math> |
|
|
|
<math>~+ \biggl\{ \frac{\bar\sigma^2\rho_0}{\varpi D} + \frac{m\bar\sigma \rho_0}{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\}\frac{\partial Q_{JT}}{\partial\varpi} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + 2 \bar\sigma {\dot\varphi}_0\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0}{ D} \biggr) \biggr] Q_{JT} ~ + {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\biggl(\frac{\bar\sigma}{\varpi} \cdot \frac{\rho_0}{D}\biggr) \biggl\{ Q_{JT} \cdot \frac{\partial (2m {\dot\varphi}_0 )}{\partial\varpi} ~ + \bar\sigma \cdot \frac{\partial Q_{JT}}{\partial\varpi} \biggr\} \, . </math> |
Each term in the first line of this two-line expression can be found in equation (2.27) of Goldreich, Goodman & Narayan (1986) — which, to facilitate comparison, has been extracted and displayed in the following framed image. But notice that the sign on a number of the terms is flipped. Notice, as well, that neither one of the terms in the second line of our expression appears in equation (2.27) of GGN86.
|
Equations (2.27) and (2.23) extracted without modification from p. 343 of Goldreich, Goodman & Narayan (1986)
"The stability of accretion tori. I - Long-wavelength modes of slender tori"
Monthly Notices of the Royal Astronomical Society, vol. 221, pp. 339-364 © Royal Astronomical Society |
It appears as though the sign on various terms is flipped because GGN86 adopted different sign conventions from Papaloizou & Pringle. Specifically, as is made clear by equation (2.23) of GGN86,
<math>~D~~~\rightarrow ~~~ -D_\mathrm{GGN} \, .</math>
Furthermore, as was deduced above when we compared expressions for the components of the perturbed velocity,
<math>~\bar\sigma~~~\rightarrow ~~~ -\sigma_\mathrm{GGN} \, .</math>
Making this pair of substitutions, our derived two-line expression becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[ \frac{ \sigma_\mathrm{GGN}^2 \rho_0^2 }{\gamma P_0} + \frac{\sigma_\mathrm{GGN}^2\rho_0 }{D_\mathrm{GGN}} \biggl( \frac{m}{\varpi} \biggr)^2 + 2 \sigma_\mathrm{GGN}{\dot\varphi}_0\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0}{ D_\mathrm{GGN}} \biggr) \biggr] Q_{JT} ~ - \sigma_\mathrm{GGN}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D_\mathrm{GGN}}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} -~ \frac{ \sigma_\mathrm{GGN}^2\rho_0 }{D_\mathrm{GGN}} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\biggl(\frac{\sigma_\mathrm{GGN}}{\varpi} \cdot \frac{\rho_0}{D_\mathrm{GGN}}\biggr) \biggl\{ Q_{JT} \cdot \frac{\partial (2m {\dot\varphi}_0 )}{\partial\varpi} ~ - \sigma_\mathrm{GGN} \cdot \frac{\partial Q_{JT}}{\partial\varpi} \biggr\} \, , </math> |
and the first line appears to exactly match equation (2.27) from GGN86. In an effort to explain why the pair of terms in the second line of our expression do not appear in the GGN86 equation, we quote directly from the text that immediately follows equation (2.27) in Goldreich, Goodman & Narayan (1986): "This is very similar to equation (2.19) for <math>~W = Q/\sigma</math> derived in PPII. The few small differences can be traced to our neglect of the azimuthal curvature of the torus through our Cartesian approximation. These terms are not important and so we expect equation (2.27) to capture all the essential physics of the narrow torus."
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |