Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/JacobiEllipsoids"

From VistrailsWiki
Jump to navigation Jump to search
(→‎Roots of the Governing Relation: Insert fixed-format "pre" Jacobi Sequence data as determined here)
(→‎Roots of the Governing Relation: Add caption to Panel A of "pre" table)
Line 489: Line 489:
</th>
</th>
</tr>
</tr>
<tr><td align="left">
<b>Panel A:</b>  Given each pair of axis ratios, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> &#8212; copied from Table IV of EFE &#8212; we converted to double-precision some fortran routines from Numerical Recipes to calculate <math>~F(\theta,k)</math> and <math>~E(\theta,k)</math>.  We subsequently evaluated the coefficients, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, using the expressions given above, then demonstrated that, in each case, the three coefficients sum to 2.0 to better than twelve digits accuracy.
</td></tr>
<tr><td align="left">
<tr><td align="left">
<pre>
<pre>

Revision as of 18:54, 26 June 2016

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Jacobi Ellipsoids

General Coefficient Expressions

As has been detailed in an accompanying chapter, the gravitational potential anywhere inside or on the surface, <math>~(a_1,a_2,a_3) ~\leftrightarrow~(a,b,c)</math>, of an homogeneous ellipsoid may be given analytically in terms of the following three coefficient expressions:

<math> ~A_1 </math>

<math> ~= </math>

<math>~2\biggl(\frac{b}{a}\biggr)\biggl(\frac{c}{a}\biggr) \biggl[ \frac{F(\theta,k) - E(\theta,k)}{k^2 \sin^3\theta} \biggr] \, , </math>

<math> ~A_3 </math>

<math> ~= </math>

<math> ~2\biggl(\frac{b}{a}\biggr) \biggl[ \frac{(b/a) \sin\theta - (c/a)E(\theta,k)}{(1-k^2) \sin^3\theta} \biggr] \, , </math>

<math> ~A_2 </math>

<math> ~= </math>

<math>~2 - (A_1+A_3) \, ,</math>

where, <math>~F(\theta,k)</math> and <math>~E(\theta,k)</math> are incomplete elliptic integrals of the first and second kind, respectively, with arguments,

<math>~\theta = \cos^{-1} \biggl(\frac{c}{a} \biggr)</math>

      and      

<math>~k = \biggl[\frac{1 - (b/a)^2}{1 - (c/a)^2} \biggr]^{1/2} \, .</math>

[ EFE, Chapter 3, §17, Eq. (32) ]

Equilibrium Conditions for Jacobi Ellipsoids

Pulling from Chapter 6 — specifically, §39 — of Chandrasekhar's EFE, we understand that the semi-axis ratios, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> associated with Jacobi ellipsoids are given by the roots of the equation,

<math>~a^2 b^2 A_{12}</math>

<math>~=</math>

<math>~c^2 A_3 \, ,</math>

[ EFE, §39, Eq. (4) ]

and the associated value of the square of the equilibrium configuration's angular velocity is,

<math>~\frac{\Omega^2}{\pi G \rho}</math>

<math>~=</math>

<math>~2B_{12} \, ,</math>

[ EFE, §39, Eq. (5) ]

where,

<math>~A_{12}</math>

<math>~\equiv</math>

<math>~-\frac{A_1-A_2}{(a^2 - b^2)} \, ,</math>

[ EFE, §21, Eq. (107) ]

<math>~B_{12}</math>

<math>~\equiv</math>

<math>~A_2 - a^2A_{12} \, .</math>

[ EFE, §21, Eq. (105) ]


Taken together, we see that, written in terms of the two primary coefficients, <math>~A_1</math> and <math>~A_3</math>, the pair of defining relations for Jacobi ellipsoids is:


<math>~f_J</math>

<math>~\equiv</math>

<math>~\biggl(\frac{b}{a}\biggr)^2 \biggl[ \frac{2(1-A_1)-A_3}{1 - (b/a)^2} \biggr]-\biggl(\frac{c}{a}\biggr)^2 A_3 =0 </math>

and

<math>~\frac{\Omega^2}{\pi G \rho}</math>

<math>~=</math>

<math>~2\biggl\{2 - (A_1+A_3) - \biggl[ \frac{2(1-A_1)-A_3}{1 - (b/a)^2} \biggr] \biggr\}</math>

Roots of the Governing Relation

To simplify notation, here we will set,

<math>~x \equiv \frac{b}{a}</math>

      and      

<math>~y \equiv \frac{c}{a} \, ,</math>

in which case the governing relation is,

<math>~f_J</math>

<math>~=</math>

<math>~\frac{x^2}{1-x^2} \biggl[ 2(1-A_1)-A_3\biggr]-y^2 A_3 =0 \, .</math>

Our plan is to employ the Newton-Raphson method to find the root(s) of the <math>~f_J = 0</math> relation, typically holding <math>~y</math> fixed and using the Newton-Raphson technique to identify the corresponding "root" value of <math>~x</math>. Using this approach, the Newton-Raphson technique requires specification of, not only the function, <math>~f_J</math>, but also its first derivative,

<math>~f_J^'</math>

<math>~=</math>

<math>~\frac{df_J}{dx} \, .</math>

Let's determine the requisite expression, using a prime superscript to indicate differentiation with respect to <math>~x</math>.

<math>~f_J^'</math>

<math>~=</math>

<math>~ \biggl[ 2(1-A_1)-A_3\biggr]\biggl[ \frac{2x}{(1-x^2)^2} \biggr] -\frac{x^2}{1-x^2} \biggl[ 2A_1^'+A_3^'\biggr] -y^2 A_3^' \, , </math>

where, given that <math>~\theta</math> does not depend on <math>~x</math>,

<math> ~A_1^' </math>

<math> ~= </math>

<math>~\frac{2y}{\sin^3\theta} \cdot \frac{d}{dx}\biggl\{ \frac{x}{k^2} \biggl[ F(\theta,k) - E(\theta,k) \biggr] \biggr\} </math>

 

<math> ~= </math>

<math>~\frac{2y}{k^3 \sin^3\theta} \cdot \biggl\{ [ F - E ] [k - 2xk^' ] +xk [ F^' - E^' ]\biggr\} \, , </math>

<math> ~A_3^' </math>

<math> ~= </math>

<math> ~\frac{2}{\sin^3\theta} \cdot \frac{d}{dx}\biggl\{ \frac{x}{(1-k^2)} \biggl[ x \sin\theta - yE(\theta,k)\biggr] \biggr\} </math>

 

<math> ~= </math>

<math> ~\frac{2}{(1-k^2)^2\sin^3\theta} \biggl\{ \biggl[ x \sin\theta - yE\biggr]\biggl[ (1-k^2) +2xkk^' \biggr] + x(1-k^2) \biggl[ \sin\theta - yE^'\biggr] \biggr\}\, , </math>

<math>~k^'</math>

<math>~=</math>

<math>~ \frac{d}{dx}\biggl[\frac{1 - x^2}{1 - y^2} \biggr]^{1/2} = \frac{-x}{(1 - x^2)^{1/2}(1 - y^2)^{1/2}} \, , </math>

<math>~F^'</math>

<math>~=</math>

<math>~ \frac{\partial F(\theta,k)}{\partial k} \cdot k^' \, , </math>

<math>~E^'</math>

<math>~=</math>

<math>~ \frac{\partial E(\theta,k)}{\partial k} \cdot k^' \, . </math>

Now, according to online WolframResearch documentation — see, in particular, the subsection titled, "Representations of Derivatives" —

<math>~\frac{\partial F(z|m)}{\partial m}</math>

<math>~=</math>

<math>~ \frac{E(z|m)}{2(1-m)m} - \frac{F(z|m)}{2m} - \frac{\sin(2z)}{4(1-m)\sqrt{1-m\sin^2(z)}} \, , </math>

and,

<math>~\frac{\partial E(z|m)}{\partial m}</math>

<math>~=</math>

<math>~\frac{E(z|m) - F(z|m)}{2m} \, ,</math>

where, <math>~z~\leftrightarrow~\theta</math>, and,

<math>~m \equiv k^2 ~~~~\Rightarrow~~~~\frac{dm}{dk} = 2k \ .</math>

Hence, we have,

<math>~F^'</math>

<math>~=</math>

<math>~ \biggl[\frac{\partial F(z|m)}{\partial m} \cdot \frac{dm}{dk}\biggr] k^' </math>

 

<math>~=</math>

<math>~ \biggl[ \frac{E(\theta,k)}{2(1-k^2)k^2} - \frac{F(\theta,k)}{2k^2} - \frac{\sin(2\theta)}{4(1-k^2)\sqrt{1-k^2\sin^2\theta}} \biggr] 2kk^' \, , </math>

<math>~E^'</math>

<math>~=</math>

<math>~ \biggl[ \frac{\partial E(z|m)}{\partial m} \cdot \frac{dm}{dk}\biggr] k^' </math>

 

<math>~=</math>

<math>~ \biggl[ E(\theta,k) - F(\theta,k) \biggr] \frac{k^'}{k} \, . </math>

This, then, gives us all of the expressions necessary to specify the derivative, <math>~f_J^'</math> analytically.


Table 1:  Double-Precision Evaluations

Related to Table IV in EFE, Chapter 6, §39 (p. 103)

Panel A: Given each pair of axis ratios, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> — copied from Table IV of EFE — we converted to double-precision some fortran routines from Numerical Recipes to calculate <math>~F(\theta,k)</math> and <math>~E(\theta,k)</math>. We subsequently evaluated the coefficients, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, using the expressions given above, then demonstrated that, in each case, the three coefficients sum to 2.0 to better than twelve digits accuracy. 

                                                                                                                                 precision
         b/a      c/a              F                   E                  A1                  A2                  A3          [2-(A1+A2+A3)]/2

        1.00   0.582724          -----               -----          5.158904180D-01     5.158904180D-01     9.682191640D-01        0.0D+00
        0.96   0.570801     9.782631357D-01     9.487496699D-01     5.024584655D-01     5.292952683D-01     9.682462661D-01        4.4D-16
        0.92   0.558330     1.009516282D+00     9.489290273D-01     4.884500698D-01     5.432292722D-01     9.683206580D-01        0.0D+00
        0.88   0.545263     1.042655826D+00     9.492826127D-01     4.738278227D-01     5.577100115D-01     9.684621658D-01        2.2D-16
        0.84   0.531574     1.077849658D+00     9.498068890D-01     4.585648648D-01     5.727687434D-01     9.686663918D-01        2.2D-16

        0.80   0.517216     1.115314984D+00     9.505192815D-01     4.426242197D-01     5.884274351D-01     9.689483451D-01       -4.4D-16
        0.76   0.502147     1.155290552D+00     9.514282210D-01     4.259717080D-01     6.047127268D-01     9.693155652D-01        2.2D-16
        0.72   0.486322     1.198053140D+00     9.525420558D-01     4.085724682D-01     6.216515450D-01     9.697759868D-01       -4.4D-16
        0.68   0.469689     1.243931393D+00     9.538724717D-01     3.903895871D-01     6.392680107D-01     9.703424022D-01        2.2D-16
        0.64   0.452194     1.293310292D+00     9.554288569D-01     3.713872890D-01     6.575860416D-01     9.710266694D-01        4.4D-16

        0.60   0.433781     1.346645618D+00     9.572180643D-01     3.515319835D-01     6.766289416D-01     9.718390749D-01       -3.3D-16
        0.56   0.414386     1.404492405D+00     9.592491501D-01     3.307908374D-01     6.964136019D-01     9.727955606D-01       -6.7D-16
        0.52   0.393944     1.467522473D+00     9.615263122D-01     3.091371405D-01     7.169543256D-01     9.739085339D-01        4.4D-16
        0.48   0.372384     1.536570313D+00     9.640523748D-01     2.865506903D-01     7.382563770D-01     9.751929327D-01       -2.2D-16
        0.44   0.349632     1.612684395D+00     9.668252052D-01     2.630231082D-01     7.603153245D-01     9.766615673D-01        8.9D-16

        0.40   0.325609     1.697213059D+00     9.698379297D-01     2.385623719D-01     7.831101146D-01     9.783275135D-01        0.0D+00
        0.36   0.300232     1.791930117D+00     9.730763540D-01     2.132011181D-01     8.065964525D-01     9.802024294D-01        2.2D-15
        0.32   0.273419     1.899227853D+00     9.765135895D-01     1.870102340D-01     8.307027033D-01     9.822870627D-01       -1.3D-15
        0.28   0.245083     2.022466812D+00     9.801112910D-01     1.601127311D-01     8.553054155D-01     9.845818534D-01       -2.4D-15
        0.24   0.215143     2.166555572D+00     9.838093161D-01     1.327137129D-01     8.802197538D-01     9.870665333D-01        1.4D-14

        0.20   0.183524     2.339102805D+00     9.875217566D-01     1.051389104D-01     9.051602520D-01     9.897008376D-01       -1.6D-14
        0.16   0.150166     2.552849055D+00     9.911267582D-01     7.790060179D-02     9.296886827D-01     9.924107155D-01       -3.4D-14
        0.12   0.115038     2.831664019D+00     9.944537935D-01     5.180880535D-02     9.531203882D-01     9.950708065D-01        1.4D-13
        0.08   0.078166     3.229072310D+00     9.972669475D-01     2.817821170D-02     9.743504218D-01     9.974713665D-01        3.9D-13
        0.04   0.039688     3.915557866D+00     9.992484565D-01     9.281550546D-03     9.914470033D-01     9.992714461D-01        9.8D-13

         b/a      c/a            omega2              angmom              5L/M                fJ              fJderiv

        1.00   0.582724     3.742297785D-01     3.037510987D-01     4.232965627D+00     0.000000000D+00     0.000000000D+00
        0.96   0.570801     3.739782202D-01     3.039551227D-01     4.235808832D+00     1.377942479D-06     1.636908401D-01
        0.92   0.558330     3.731876801D-01     3.046006837D-01     4.244805137D+00    -6.821687132D-07     1.676406830D-01
        0.88   0.545263     3.717835971D-01     3.057488283D-01     4.260805266D+00     8.533280272D-07     1.715558312D-01
        0.84   0.531574     3.696959199D-01     3.074667323D-01     4.284745355D+00    -4.622993727D-08     1.754024874D-01
        0.80   0.517216     3.668370069D-01     3.098368632D-01     4.317774645D+00     2.805300664D-08     1.791408327D-01
        0.76   0.502147     3.631138118D-01     3.129555079D-01     4.361234951D+00     3.221800126D-07     1.827219476D-01
        0.72   0.486322     3.584232032D-01     3.169377270D-01     4.416729718D+00     3.274773094D-08     1.860866255D-01
        0.68   0.469689     3.526490289D-01     3.219229588D-01     4.486202108D+00     1.202999164D-08     1.891636215D-01
        0.64   0.452194     3.456641138D-01     3.280805511D-01     4.572012092D+00     2.681560312D-07     1.918668912D-01
        0.60   0.433781     3.373298891D-01     3.356184007D-01     4.677056841D+00     1.037186290D-08     1.940927000D-01
        0.56   0.414386     3.274928085D-01     3.447962894D-01     4.804956583D+00     1.071021385D-07     1.957166395D-01
        0.52   0.393944     3.159887358D-01     3.559412795D-01     4.960269141D+00     8.098003093D-08     1.965890756D-01
        0.48   0.372384     3.026414267D-01     3.694732246D-01     5.148845443D+00     1.255768368D-07     1.965308751D-01
        0.44   0.349632     2.872670174D-01     3.859399647D-01     5.378319986D+00     1.329168636D-08     1.953277019D-01
        0.40   0.325609     2.696779847D-01     4.060726774D-01     5.658882201D+00    -9.783004411D-08     1.927241063D-01
        0.36   0.300232     2.496925963D-01     4.308722159D-01     6.004479614D+00     1.044268276D-07     1.884168286D-01
        0.32   0.273419     2.271530240D-01     4.617497270D-01     6.434777459D+00    -4.469279448D-08     1.820477545D-01
        0.28   0.245083     2.019461513D-01     5.007767426D-01     6.978643856D+00     7.996820889D-08     1.731984783D-01
        0.24   0.215143     1.740514751D-01     5.511400218D-01     7.680488329D+00     1.099319693D-07     1.613864645D-01
        0.20   0.183524     1.436093757D-01     6.180687545D-01     8.613182979D+00     5.068010978D-08     1.460685065D-01
        0.16   0.150166     1.110438660D-01     7.109267615D-01     9.907218635D+00    -2.170751250D-08     1.266576761D-01
        0.12   0.115038     7.728058393D-02     8.487699974D-01     1.182815219D+01     3.613784147D-09     1.025686850D-01
        0.08   0.078166     4.416740942D-02     1.079303624D+00     1.504078558D+01     3.319018649D-08     7.332782508D-02
        0.04   0.039688     1.541513490D-02     1.582762691D+00     2.205680933D+01    -6.674246644D-09     3.882477311D-02

   b/a       c/a

  0.990699  0.580000
  0.901558  0.552381
  0.820783  0.524762
  0.747135  0.497143
  0.679613  0.469524
  0.617393  0.441905
  0.559798  0.414286
  0.506257  0.386667
  0.456291  0.359048
  0.409492  0.331429
  0.365507  0.303810
  0.324034  0.276190
  0.284807  0.248571
  0.247591  0.220952
  0.212179  0.193333
  0.178382  0.165714
  0.146026  0.138095
  0.114948  0.110476
  0.084989  0.082857
  0.055982  0.055238
  0.027738  0.027619

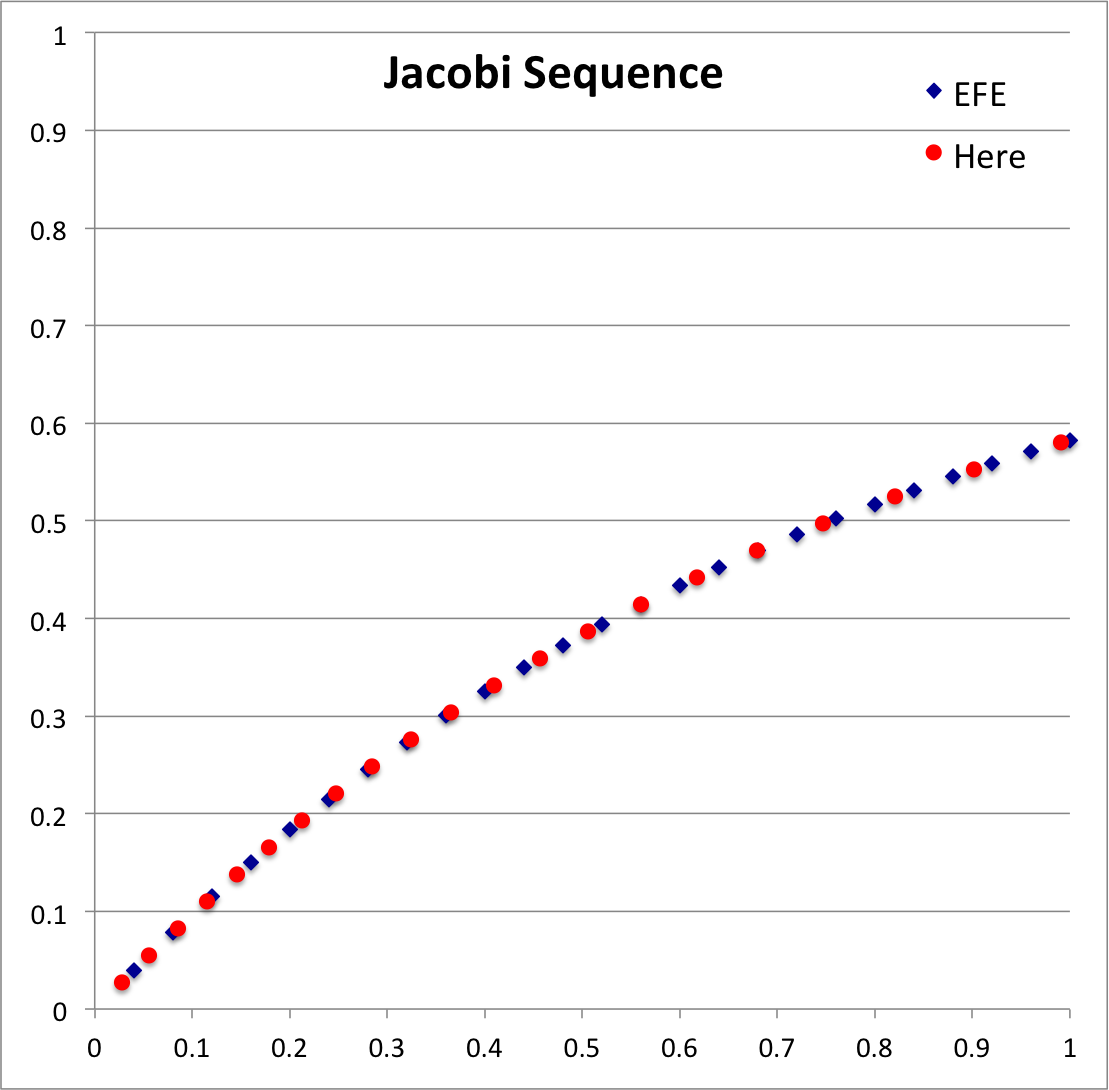
Sequence Plots

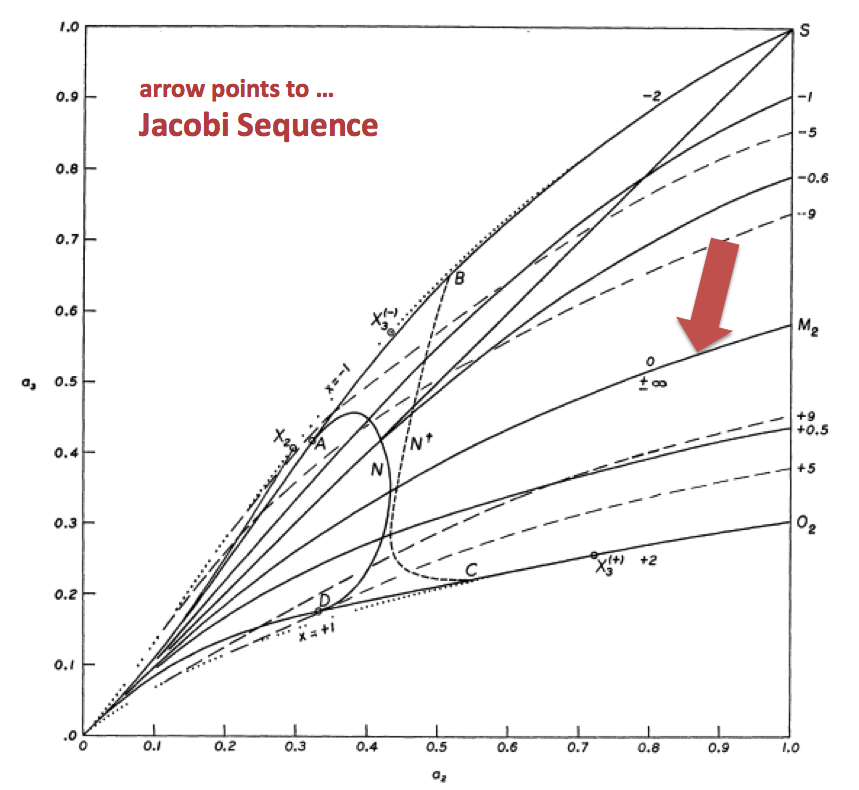
Jacobi Sequence: (blue) Points defined by data in Table IV of EFE, Chapter 6, §39 (p. 103); (red) points generated here from above-defined roots of the governing relation. Figure 2 extracted† from p. 902 of S. Chandrasekhar (1965)

"The Equilibrium and the Stability of the Riemann Ellipsoids. I"

ApJ, vol. 142, pp. 890-921 © American Astronomical Society

Jacobi Sequence

Chandrasekhar Figure2

  †Original figure has been annotated (maroon-colored text and arrow added) for clarification.

See Also


Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/ThreeDimensionalConfigurations/JacobiEllipsoids&oldid=12022"