User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1) and (Pt. 2). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Various Coordinate Frames
Riemann-Derived Expressions
|
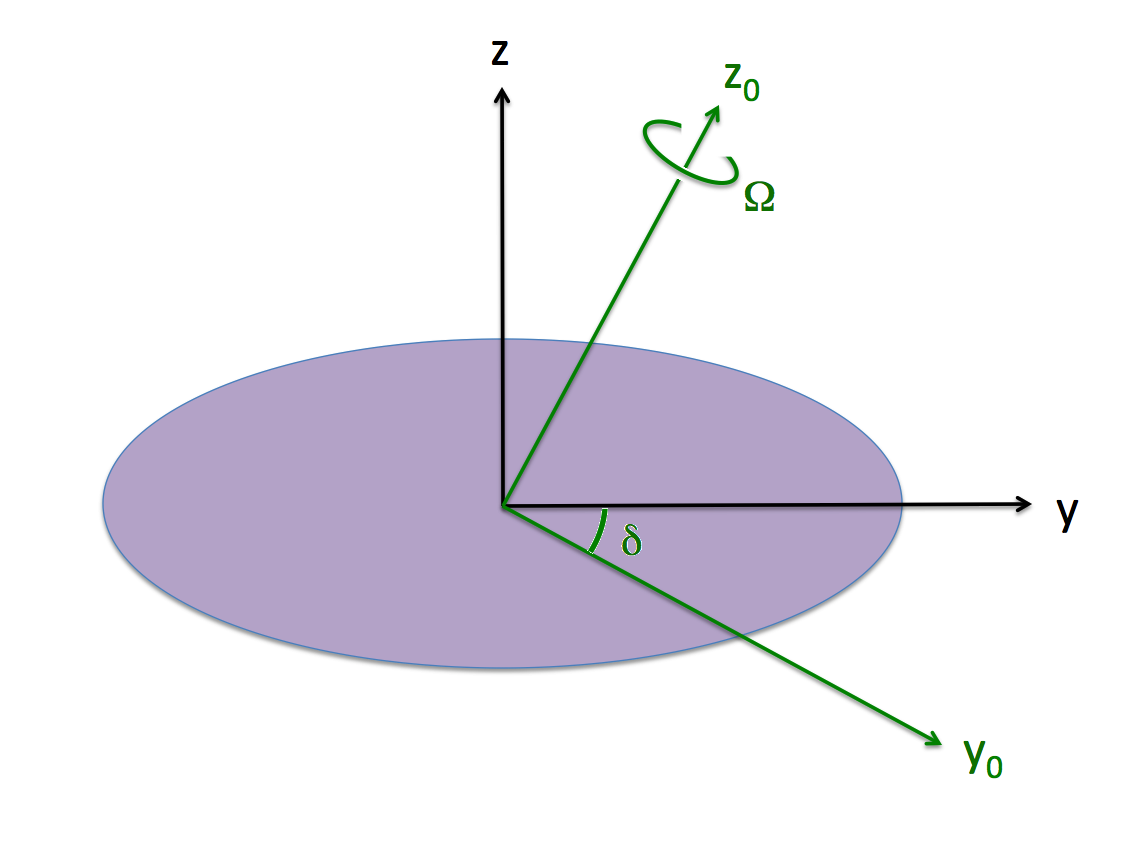
The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat{k}_0}\Omega_0 \, .</math> |
Also as illustrated, the "body frame," which is attached to and aligned with the principal axes of the purple ellipsoid, is tilted at an angle, <math>~\delta</math>, with respect to the inertial frame. Hence, as viewed from the body frame, we have,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\biggl[ \boldsymbol{\hat\jmath }\sin\delta + \boldsymbol{\hat{k} }\cos\delta \biggr]\Omega_0 \, .</math> |
Now, adhering to the notation used by [EFE] — see, for example, the first paragraph of §51 (p. 156) — we should write,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat\jmath }\Omega_2 + \boldsymbol{\hat{k} }\Omega_3 ~~~~~\Rightarrow ~~~ \Omega_2 = \Omega_0\sin\delta </math> and, <math>~\Omega_3 = \Omega_0\cos\delta \, .</math> |
This means that,
|
<math>~\Omega_0</math> |
<math>~=</math> |
<math>~ \biggl[\Omega_2^2 + \Omega_3^2 \biggr]^{1 / 2} </math> and, <math>~\delta = \tan^{-1}\biggl[ \frac{\Omega_2}{\Omega_3} \biggr] \, .</math> |
As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids, [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x1, x2, x3) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are,
|
<math>~\dot{x} = u_1 = \boldsymbol{\hat\imath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math> |
|
<math>~\dot{y} = u_2 = \boldsymbol{\hat\jmath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~- \gamma \Omega_3 x</math> |
<math>~=</math> |
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math> |
|
<math>~\dot{z} = u_3 = \boldsymbol{\hat{k}} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~+ \beta \Omega_2 x</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math> |
where,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math> |
|
Rotating-Frame Vorticity
|
||||||||||
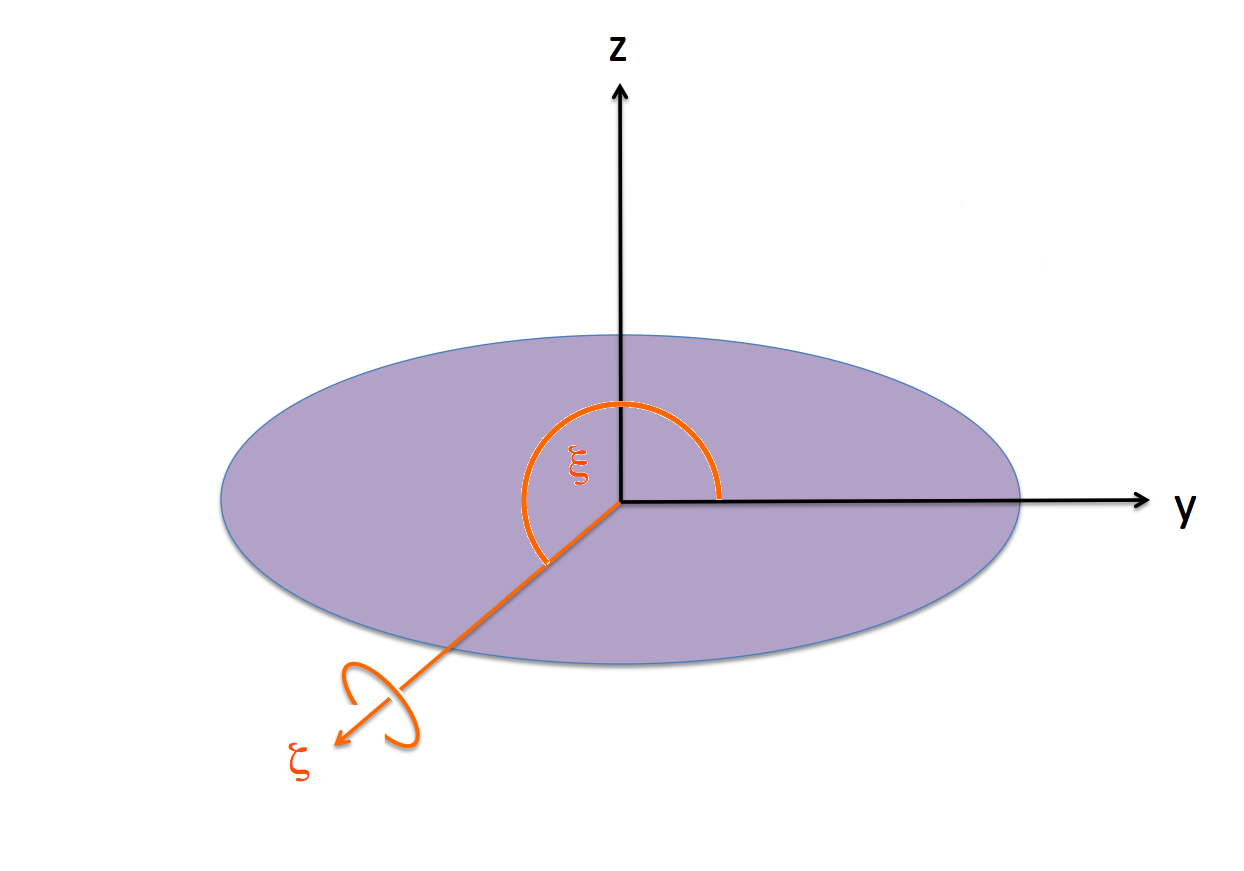
For our chosen Example Type I Ellipsoid, we have, <math>~\zeta_2 = -2.2794</math> and <math>~\Omega_3 = -1.9637</math>, in which case, <math>~\zeta_\mathrm{rot} = (\zeta_2^2 + \zeta_3^2)^{1 / 2} = 2.2794</math> and <math>~\xi \equiv \tan^{-1}[\zeta_2/\zeta_3] = 4.0013 ~\mathrm{rad} = 229.26^\circ</math>. |
||||||||||
Tipped Orbit Planes
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. (See the yellow-dotted orbits in Figure panels 1a and 1b below). As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = 0 and dz'/dt = 0, and the planar orbit is defined by the expression for an,
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, .</math> |
As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y_0</math> |
<math>~=</math> |
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> |
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_0 - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |