Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3"
| (33 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__FORCETOC__<!-- will force the creation of a Table of Contents --> | __FORCETOC__<!-- will force the creation of a Table of Contents --> | ||
<!-- __NOTOC__ will force TOC off --> | <!-- __NOTOC__ will force TOC off --> | ||
=Challenges Constructing Ellipsoidal-Like Configurations (Pt. | =Challenges Constructing Ellipsoidal-Like Configurations (Pt. 3)= | ||
This chapter extends the accompanying chapters titled, [[User:Tohline/ThreeDimensionalConfigurations/Challenges|''Construction Challenges (Pt. 1)'']] and [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2|''(Pt. 2)'']]. The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames. | This chapter extends the accompanying chapters titled, [[User:Tohline/ThreeDimensionalConfigurations/Challenges|''Construction Challenges (Pt. 1)'']] and [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2|''(Pt. 2)'']]. The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames. | ||
| Line 9: | Line 9: | ||
==Various Coordinate Frames== | ==Various Coordinate Frames== | ||
<table border="1" align=" | ===Riemann-Derived Expressions=== | ||
<table border="0" cellpadding="10" align="right" width="30%"><tr><td align="center"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr><td align="center"> | <tr><td align="center"> | ||
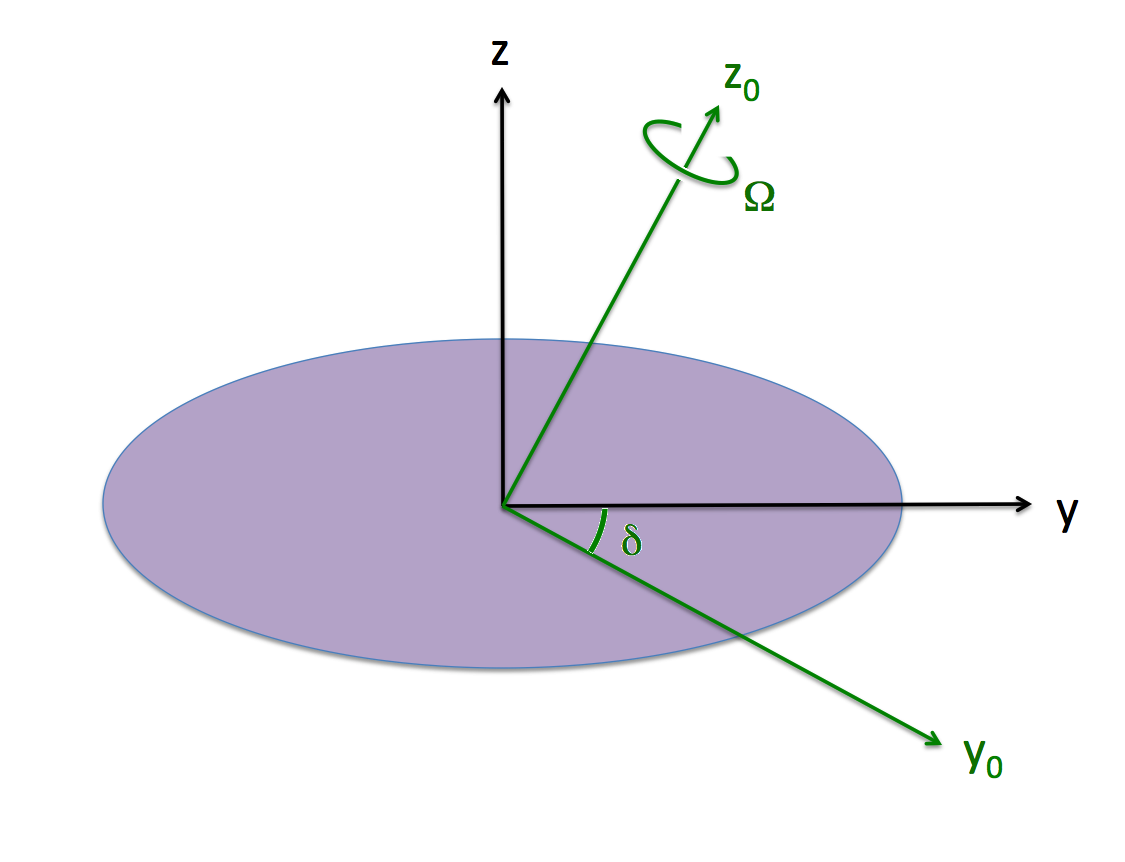
''Inertial Frame'' (green with subscript "0") <br />and ''Body Frame'' (black and unsubscripted). | ''Inertial Frame'' (green with subscript "0") <br />and ''Body Frame'' (black and unsubscripted). | ||
| Line 15: | Line 17: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center">[[File: | <td align="center">[[File:InertialAxes05.png|400px|Inertial and Body Frames]]</td> | ||
</tr> | |||
<tr><td align="center"> | |||
For our chosen [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Case_I|Example Type I Ellipsoid]], we have, <math>~\Omega_2 = 0.3639</math> and <math>~\Omega_3 = 0.6633</math>, in which case, <math>~\Omega_0 = 0.7566</math> and <math>~\delta = 0.5018 ~\mathrm{rad} = 28.75^\circ</math>. | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
</td></tr></table> | |||
The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is, | The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is, | ||
| Line 34: | Line 41: | ||
</tr> | </tr> | ||
</table> | </table> | ||
Also as illustrated, the "body frame," which is attached to and aligned with the principal axes of the purple ellipsoid, is tilted at an angle, <math>~\delta</math>, with respect to the inertial frame. | Also as illustrated, the "body frame," which is attached to and aligned with the principal axes of the purple ellipsoid, is tilted at an angle, <math>~\delta</math>, with respect to the inertial frame. Hence, as viewed from the ''body'' frame, we have, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 86: | Line 93: | ||
</tr> | </tr> | ||
</table> | </table> | ||
As we have summarized in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#EFEvelocities|accompanying discussion]] of Riemann Type 1 ellipsoids, [[User:Tohline/Appendix/References#EFE|[<font color="red">EFE</font>] ]] provides an expression for the velocity vector of each fluid element, given its instantaneous ''body''-coordinate position (x, y, z) = (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are, | As we have summarized in an [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#EFEvelocities|accompanying discussion]] of Riemann Type 1 ellipsoids, [[User:Tohline/Appendix/References#EFE|[<font color="red">EFE</font>] ]] provides an expression for the velocity vector of each fluid element, given its instantaneous ''body''-coordinate position (x, y, z) = (x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are, | ||
| Line 101: | Line 100: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\dot{x} = u_1</math> | <math>~\dot{x} = u_1 = \boldsymbol{\hat\imath} \cdot \boldsymbol{u}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 119: | Line 118: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\dot{y} = u_2</math> | <math>~\dot{y} = u_2 = \boldsymbol{\hat\jmath} \cdot \boldsymbol{u}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 137: | Line 136: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\dot{z} = u_3</math> | <math>~\dot{z} = u_3 = \boldsymbol{\hat{k}} \cdot \boldsymbol{u}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 153: | Line 152: | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, | <span id="betagamma">where,</span> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 184: | Line 183: | ||
</table> | </table> | ||
<table border="1" cellpadding="8" width="90%" align="center"><tr><td align="left"> | <table border="1" cellpadding="8" width="90%" align="center"> | ||
<tr><td align="left" colspan="2"> | |||
<div align="center">'''Rotating-Frame Vorticity'''</div> | <div align="center">'''Rotating-Frame Vorticity'''</div> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 239: | Line 243: | ||
</table> | </table> | ||
For our chosen [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Case_I|Example Type I Ellipsoid]], we have, <math>~\zeta_2 = -2.2794</math> and <math>~\Omega_3 = -1.9637</math>, in which case, <math>~\zeta_\mathrm{rot} = (\zeta_2^2 + \zeta_3^2)^{1 / 2} = 2.2794</math> and <math>~\tan^{-1}[\zeta_2/\zeta_3] = 4.0013 ~\mathrm{rad} = 229.26^\circ</math>. | For our chosen [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Case_I|Example Type I Ellipsoid]], we have, <math>~\zeta_2 = -2.2794</math> and <math>~\Omega_3 = -1.9637</math>, in which case, <math>~\zeta_\mathrm{rot} = (\zeta_2^2 + \zeta_3^2)^{1 / 2} = 2.2794</math> and <math>~\xi \equiv \tan^{-1}[\zeta_2/\zeta_3] = 4.0013 ~\mathrm{rad} = 229.26^\circ</math>. | ||
</td> | |||
<td align="center"> | |||
[[File:VorticityAxis04.png|350px|center|Vorticity Axis]] | |||
</td> | |||
</tr> | |||
</table> | |||
===Tipped Orbit Planes=== | |||
====Summary==== | |||
In a [[User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI#Try_Again|separate discussion]], we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = constant and dz'/dt = 0, and the planar orbit is defined by the expression for an, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><font color="maroon">'''Off-Center Ellipse'''</font></td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c(z')}{y_\mathrm{max}} \biggr]^2 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="10" align="right" width="30%"><tr><td align="center"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr><td align="center"> | |||
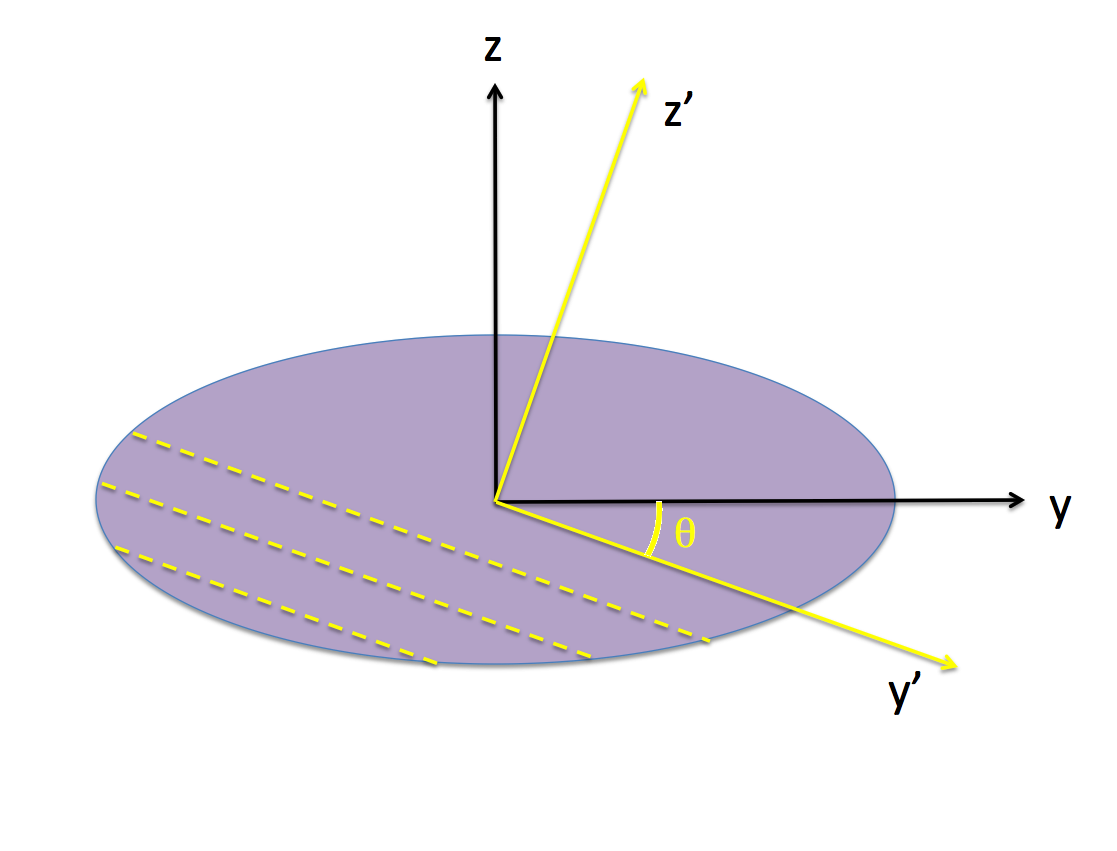
''Tipped Orbit Frame'' (yellow, primed) <br /> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center">[[File:TippedAxes03.png|350px|Tipped Orbital Planes]]</td> | |||
</tr> | |||
<tr><td align="center"> | |||
Given that b/a = 1.25 and c/a = 0.4703 for our chosen [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2#Example_Equilibrium_Model|Example Type I Ellipsoid]], we find that, <math>~\theta = - 0.3320 ~\mathrm{rad} = -19.02^\circ</math>. | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | </td></tr></table> | ||
Notice that the offset, <math>~y_c</math>, is a function of the tipped plane's vertical coordinate, <math>~z'</math>. As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> | |||
</td> | |||
<td align="center"> and, | |||
<td align="right"> | |||
<math>~y' - y_c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\dot{x}'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_c - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> | |||
</td> | |||
<td align="center"> and, | |||
<td align="right"> | |||
<math>~\dot{y}' </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
As has been summarized in an [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2#Try_Tipped_Plane_Again|accompanying discussion]], we have determined that (numerical value given for our chosen example Type I ellipsoid), | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="center" | <td align="right"> | ||
<math>~\tan\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} | |||
= | |||
- \frac{\beta \Omega_2}{\gamma \Omega_3} | |||
= | |||
-0.34479\, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
< | </table> | ||
< | where, <math>~\beta</math> and <math>~\gamma</math> are as [[#betagamma|defined above]]. Also, | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 263: | Line 368: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{a^2}{b^2 c^2} (c^2\cos^2\theta + b^2\sin^2\theta) | |||
= 1.05238 \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 269: | Line 377: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~{\dot\varphi}^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 275: | Line 383: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] | |||
= 1.68818\, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 281: | Line 393: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~y_c</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 287: | Line 399: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~z_0\cos\ | <math>~+ \frac{z' b^2 \tan\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} | ||
= | |||
+z' \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} | |||
= | |||
\biggl( \frac{z'}{ \cos\theta }\biggr)(-1.40038) | |||
\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Note that this last expression has been obtained by making the substitutions, <math>~y_0 \rightarrow y_c</math> and <math>~z_0 \rightarrow -z'/\cos\theta</math>, in the [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2#OffCenter|accompanying derivation's expression]] for <math>~y_0</math>. | |||
====Demonstration==== | |||
In order to transform a vector from the "tipped orbit" frame (primed coordinates) to the "body" frame (unprimed), we use the following mappings of the three unit vectors: | |||
<table border="1" align="center" width="40%" cellpadding="8"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat\imath'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\boldsymbol{\hat\imath} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat\jmath'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{k}'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\boldsymbol{\hat\jmath}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | </td></tr></table> | ||
< | |||
Given that, by design in our "tipped orbit" frame, there is no vertical motion — that is, <math>~\dot{z}' = 0</math> — mapping the (primed coordinate) velocity to the body (unprimed) coordinate is particularly straightforward. Specifically, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\boldsymbol{u'}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 304: | Line 466: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~x</math> | <math>~ | ||
\boldsymbol{\hat\imath'} \dot{x}' | |||
+ | |||
\boldsymbol{\hat\jmath'} \dot{y}' | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 310: | Line 476: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~~~\rightarrow~~</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\boldsymbol{\hat\imath} \dot{x}' | |||
+ | |||
[\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \dot{y}' | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 322: | Line 492: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 328: | Line 498: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\boldsymbol{\hat\imath} \biggl\{ | |||
(y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi | |||
\biggr\} | |||
+ | |||
[\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \biggl\{ | |||
x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi | |||
\biggr\} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | Recognizing, [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2#Tipped_Orbital_Plane|as before]], that the relevant coordinate mapping is, | ||
<table border="1" align="center" width="40%" cellpadding="8"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~y\cos\theta + z\sin\theta \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~z'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~z\cos\theta - y\sin\theta \, ,</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
</td></tr></table> | |||
we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="left"> | <td align="right"> | ||
<math>~\boldsymbol{u'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~~~\rightarrow~~~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\boldsymbol{\hat\imath} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - z\sin\theta\biggr\} | |||
+ | |||
\boldsymbol{\hat\jmath} \dot\varphi | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\biggr\{ x\cos\theta \biggr\} | |||
+ | |||
\boldsymbol{\hat{k}} \dot\varphi | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\biggr\{ x\sin\theta \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\boldsymbol{\hat\ | <math>~y_c</math> | ||
</td> | |||
<td align="center"> | |||
<math>~~~\rightarrow~~~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+[z\cos\theta - y\sin\theta] \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} | |||
\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Written in terms of the "body" frame coordinates, therefore, the 2<sup>nd</sup> and 3<sup>rd</sup> components of this velocity vector are, respectively: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat\jmath}\cdot \boldsymbol{u'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x \dot\varphi | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x \biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] | |||
\biggr\}^{1 / 2} | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\cos\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x \biggl\{ \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{\hat{k}}\cdot \boldsymbol{u'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x \dot\varphi | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\sin\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 347: | Line 673: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
x \biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] | |||
\biggr\}^{1 / 2} | |||
\biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) | |||
\sin\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
\biggr\} | |||
\tan\theta | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 353: | Line 701: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 359: | Line 707: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
x \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
\biggr\} | |||
\biggl\{ | |||
- \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 365: | Line 719: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 371: | Line 725: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
-x \biggl\{ \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] | |||
\biggr\} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
These expressions perfectly match the body-coordinate expressions derived by Riemann (see [[#Riemann-Derived_Expressions|above]]) for, respectively, <math>~\dot{y}</math> and <math>~\dot{z}</math>. The 1<sup>st</sup> component is, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\boldsymbol | <math>~\boldsymbol{\hat\imath}\cdot \boldsymbol{u'}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 388: | Line 744: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - z\sin\theta\biggr\}</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 394: | Line 751: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 400: | Line 757: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] | |||
\biggr\}^{1 / 2} | |||
\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) | |||
\biggl\{y_c | |||
- y\cos\theta - z\sin\theta\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 | |||
\biggl\{\frac{y_c}{\cos\theta} | |||
- y - z\tan\theta\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 406: | Line 787: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 412: | Line 793: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggl\{ | ||
\zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta} | |||
-~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
+~ z\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</td> | <tr> | ||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggl\{ | |||
\zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta} | |||
-~y\cdot \zeta_3\biggl[ \frac{a^2}{a^2 + b^2} \biggr] \frac{b^2}{a^2} | |||
+~ z\cdot \zeta_2\biggl[ \frac{a^2}{a^2 + c^2} \biggr] \frac{c^2}{a^2} | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
So, implementing the mapping of <math>~y_c</math>, the first term inside the curly braces becomes, | |||
<table border="0" cellpadding="5" align="center"> | |||
== | <tr> | ||
<td align="right"> | |||
<math>~\zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~~~\rightarrow~~~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\zeta_3}{\cos\theta}\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ | |||
+[z\cos\theta - y\sin\theta] \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ -y\tan^2\theta \biggr\} | |||
+ | |||
\zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr]\tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ z \biggr\} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 437: | Line 862: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
-~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
- | |||
z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl(\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~~~\rightarrow~~~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} - | |||
z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<div align="left"> | |||
<math> | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr]^2~=~\frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) | |||
</math> | |||
<math> | |||
\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr]^2 \biggl[ 1 + \tan^2\theta \biggr]~=~\frac{a^2}{b^2c^2} (c^2 + b^2\tan^2\theta) | |||
</math> | |||
</div> | |||
Therefore, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\boldsymbol{\hat\imath}\cdot \boldsymbol{u'}</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} - | |||
z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
~+~ | |||
\biggl\{ | |||
z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] | |||
-~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] | |||
\biggr\} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 452: | Line 928: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~x_\mathrm{max}\ | <math>~ | ||
-~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
-~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 | |||
~+~ | |||
z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 | |||
-~z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} | |||
</math> | |||
</td> | </td> | ||
< | </tr> | ||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 462: | Line 946: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~y_\mathrm{max}\ | <math>~ | ||
-~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \biggl\{ \frac{b^2}{c^2} \cdot \tan^2\theta | |||
+\frac{b^2}{a^2} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr\} | |||
~+~ | |||
z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 | |||
-~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 468: | Line 958: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 474: | Line 964: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- | <math>~ | ||
-~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \biggl\{ \frac{b^2}{c^2} \cdot \tan^2\theta | |||
+ \frac{1}{c^2} (c^2\cos^2\theta + b^2\sin^2\theta) \biggr\} | |||
~+~ | |||
z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) | |||
-~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} | |||
</math> | |||
</td> | </td> | ||
< | </tr> | ||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 484: | Line 982: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \frac{1}{c^2\cos^2\theta}\biggl\{b^2 \sin^2\theta | |||
+ (c^2\cos^2\theta + b^2\sin^2\theta)\cos^2\theta \biggr\} | |||
~+~ | |||
z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) | |||
-~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 494: | Line 998: | ||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2|Construction Challenges (Pt. 2)]] | * [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2|Construction Challenges (Pt. 2)]] | ||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3|Construction Challenges (Pt. 3)]] | * [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt3|Construction Challenges (Pt. 3)]] | ||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt4|Construction Challenges (Pt. 4)]] | |||
* [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt5|Construction Challenges (Pt. 5)]] | |||
* Related discussions of models viewed from a rotating reference frame: | * Related discussions of models viewed from a rotating reference frame: | ||
** [[User:Tohline/PGE/RotatingFrame#Rotating_Reference_Frame|PGE]] | ** [[User:Tohline/PGE/RotatingFrame#Rotating_Reference_Frame|PGE]] | ||
Latest revision as of 21:51, 11 May 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 3)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1) and (Pt. 2). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Various Coordinate Frames
Riemann-Derived Expressions
|
The purple (ellipsoidal) configuration is spinning with frequency, <math>~\Omega_0</math> about the <math>~z_0</math>-axis of the "inertial frame," as illustrated; that is,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat{k}_0}\Omega_0 \, .</math> |
Also as illustrated, the "body frame," which is attached to and aligned with the principal axes of the purple ellipsoid, is tilted at an angle, <math>~\delta</math>, with respect to the inertial frame. Hence, as viewed from the body frame, we have,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\biggl[ \boldsymbol{\hat\jmath }\sin\delta + \boldsymbol{\hat{k} }\cos\delta \biggr]\Omega_0 \, .</math> |
Now, adhering to the notation used by [EFE] — see, for example, the first paragraph of §51 (p. 156) — we should write,
|
<math>~\boldsymbol\Omega</math> |
<math>~=</math> |
<math>~\boldsymbol{\hat\jmath }\Omega_2 + \boldsymbol{\hat{k} }\Omega_3 ~~~~~\Rightarrow ~~~ \Omega_2 = \Omega_0\sin\delta </math> and, <math>~\Omega_3 = \Omega_0\cos\delta \, .</math> |
This means that,
|
<math>~\Omega_0</math> |
<math>~=</math> |
<math>~ \biggl[\Omega_2^2 + \Omega_3^2 \biggr]^{1 / 2} </math> and, <math>~\delta = \tan^{-1}\biggl[ \frac{\Omega_2}{\Omega_3} \biggr] \, .</math> |
As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids, [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x1, x2, x3) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are,
|
<math>~\dot{x} = u_1 = \boldsymbol{\hat\imath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math> |
|
<math>~\dot{y} = u_2 = \boldsymbol{\hat\jmath} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~- \gamma \Omega_3 x</math> |
<math>~=</math> |
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math> |
|
<math>~\dot{z} = u_3 = \boldsymbol{\hat{k}} \cdot \boldsymbol{u}</math> |
<math>~=</math> |
<math>~+ \beta \Omega_2 x</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math> |
where,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math> |
|
Rotating-Frame Vorticity
|
||||||||||
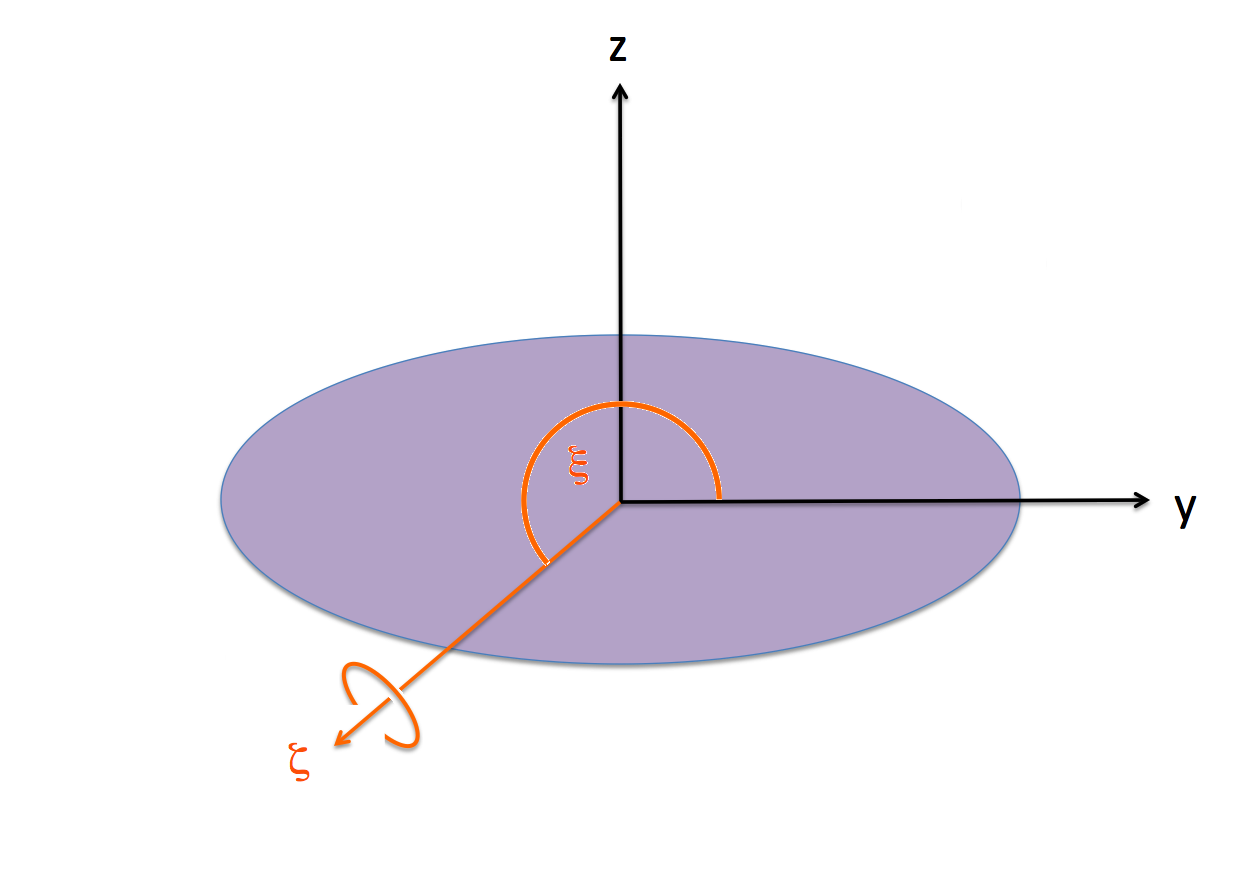
For our chosen Example Type I Ellipsoid, we have, <math>~\zeta_2 = -2.2794</math> and <math>~\Omega_3 = -1.9637</math>, in which case, <math>~\zeta_\mathrm{rot} = (\zeta_2^2 + \zeta_3^2)^{1 / 2} = 2.2794</math> and <math>~\xi \equiv \tan^{-1}[\zeta_2/\zeta_3] = 4.0013 ~\mathrm{rad} = 229.26^\circ</math>. |
||||||||||
Tipped Orbit Planes
Summary
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = constant and dz'/dt = 0, and the planar orbit is defined by the expression for an,
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c(z')}{y_\mathrm{max}} \biggr]^2 \, .</math> |
|
Notice that the offset, <math>~y_c</math>, is a function of the tipped plane's vertical coordinate, <math>~z'</math>. As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y_c</math> |
<math>~=</math> |
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> |
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_c - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> |
As has been summarized in an accompanying discussion, we have determined that (numerical value given for our chosen example Type I ellipsoid),
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} = - \frac{\beta \Omega_2}{\gamma \Omega_3} = -0.34479\, , </math> |
where, <math>~\beta</math> and <math>~\gamma</math> are as defined above. Also,
|
<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math> |
<math>~=</math> |
<math>~ \frac{a^2}{b^2 c^2} (c^2\cos^2\theta + b^2\sin^2\theta) = 1.05238 \, , </math> |
|
<math>~{\dot\varphi}^2 </math> |
<math>~=</math> |
<math>~ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] = 1.68818\, , </math> |
|
<math>~y_c</math> |
<math>~=</math> |
<math>~+ \frac{z' b^2 \tan\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} = +z' \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} = \biggl( \frac{z'}{ \cos\theta }\biggr)(-1.40038) \, .</math> |
Note that this last expression has been obtained by making the substitutions, <math>~y_0 \rightarrow y_c</math> and <math>~z_0 \rightarrow -z'/\cos\theta</math>, in the accompanying derivation's expression for <math>~y_0</math>.
Demonstration
In order to transform a vector from the "tipped orbit" frame (primed coordinates) to the "body" frame (unprimed), we use the following mappings of the three unit vectors:
|
Given that, by design in our "tipped orbit" frame, there is no vertical motion — that is, <math>~\dot{z}' = 0</math> — mapping the (primed coordinate) velocity to the body (unprimed) coordinate is particularly straightforward. Specifically,
|
<math>~\boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' </math> |
|
|
<math>~~~\rightarrow~~</math> |
<math>~ \boldsymbol{\hat\imath} \dot{x}' + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \dot{y}' </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath} \biggl\{ (y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi \biggr\} + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \biggl\{ x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi \biggr\} \, . </math> |
Recognizing, as before, that the relevant coordinate mapping is,
|
we have,
|
<math>~\boldsymbol{u'}</math> |
<math>~~~\rightarrow~~~</math> |
<math>~ \boldsymbol{\hat\imath} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - z\sin\theta\biggr\} + \boldsymbol{\hat\jmath} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\cos\theta \biggr\} + \boldsymbol{\hat{k}} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\sin\theta \biggr\} \, , </math> |
where,
|
<math>~y_c</math> |
<math>~~~\rightarrow~~~</math> |
<math>~ +[z\cos\theta - y\sin\theta] \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \, .</math> |
Written in terms of the "body" frame coordinates, therefore, the 2nd and 3rd components of this velocity vector are, respectively:
|
<math>~\boldsymbol{\hat\jmath}\cdot \boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ x \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \cos\theta </math> |
|
|
<math>~=</math> |
<math>~ x \biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \biggr\}^{1 / 2} \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \cos\theta </math> |
|
|
<math>~=</math> |
<math>~ x \biggl\{ \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggr\} \, , </math> |
|
<math>~\boldsymbol{\hat{k}}\cdot \boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ x \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \sin\theta </math> |
|
|
<math>~=</math> |
<math>~ x \biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \biggr\}^{1 / 2} \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \sin\theta </math> |
|
|
<math>~=</math> |
<math>~ x \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggr\} \tan\theta </math> |
|
|
<math>~=</math> |
<math>~ x \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggr\} \biggl\{ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -x \biggl\{ \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggr\} \, . </math> |
These expressions perfectly match the body-coordinate expressions derived by Riemann (see above) for, respectively, <math>~\dot{y}</math> and <math>~\dot{z}</math>. The 1st component is,
|
<math>~\boldsymbol{\hat\imath}\cdot \boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - z\sin\theta\biggr\}</math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \biggr\}^{1 / 2} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \biggl\{y_c - y\cos\theta - z\sin\theta\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggl\{\frac{y_c}{\cos\theta} - y - z\tan\theta\biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta} -~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] +~ z\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggl\{ \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta} -~y\cdot \zeta_3\biggl[ \frac{a^2}{a^2 + b^2} \biggr] \frac{b^2}{a^2} +~ z\cdot \zeta_2\biggl[ \frac{a^2}{a^2 + c^2} \biggr] \frac{c^2}{a^2} \biggr\} \, . </math> |
So, implementing the mapping of <math>~y_c</math>, the first term inside the curly braces becomes,
|
<math>~\zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta}</math> |
<math>~~~\rightarrow~~~</math> |
<math>~ \frac{\zeta_3}{\cos\theta}\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ +[z\cos\theta - y\sin\theta] \tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ -y\tan^2\theta \biggr\} + \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr]\tan\theta \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ z \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} - z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \biggl[\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{y_c}{\cos\theta}</math> |
<math>~~~\rightarrow~~~</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} - z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} </math> |
<math> \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr]^2~=~\frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) </math>
<math> \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr]^2 \biggl[ 1 + \tan^2\theta \biggr]~=~\frac{a^2}{b^2c^2} (c^2 + b^2\tan^2\theta) </math>
Therefore,
|
<math>~\boldsymbol{\hat\imath}\cdot \boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} - z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} ~+~ \biggl\{ z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] -~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggr\} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} -~y\cdot \zeta_3\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 ~+~ z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 -~z \cdot \zeta_2 \biggl[ \frac{c^2 }{a^2 + c^2} \biggr] \frac{a^2}{c^2} \biggl\{ \tan^2\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \biggl\{ \frac{b^2}{c^2} \cdot \tan^2\theta +\frac{b^2}{a^2} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr\} ~+~ z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 -~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \biggl\{ \frac{b^2}{c^2} \cdot \tan^2\theta + \frac{1}{c^2} (c^2\cos^2\theta + b^2\sin^2\theta) \biggr\} ~+~ z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) -~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~y \cdot \zeta_3 \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \frac{1}{c^2\cos^2\theta}\biggl\{b^2 \sin^2\theta + (c^2\cos^2\theta + b^2\sin^2\theta)\cos^2\theta \biggr\} ~+~ z\cdot \zeta_2\biggl[ \frac{c^2}{a^2 + c^2} \biggr] \biggl\{ \frac{a^2}{b^2c^2} (c^2\cos^2\theta + b^2\sin^2\theta) -~ \frac{a^2}{c^2} \cdot \tan^2\theta \biggr\} </math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Construction Challenges (Pt. 4)
- Construction Challenges (Pt. 5)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |