User:Tohline/SphericallySymmetricConfigurations/IntroductorySummary

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Applications
Spherically Symmetric Configurations
Structure:
Here we show how the set of principal governing equations (PGEs) can be solved to determine the equilibrium structure of spherically symmetric fluid configurations — such as individual, nonrotating stars or protostellar gas clouds.
Isolated Configurations
After supplementing the PGEs by specifying an equation of state of the fluid, the system of equations is usually solved by employing one of three techniques to obtain a "detailed force-balanced" model that provides the radius, <math>~R_\mathrm{eq}</math>, of the equilibrium configuration — given its mass, <math>~M</math>, and central pressure, <math>~P_c</math>, for example — as well as details regarding the internal radial profiles of the fluid density and fluid pressure. If a polytropic equation of state,
<math>~P = K_\mathrm{n} \rho^{1+1/n}</math>
is adopted, for example, a detailed force-balanced model is fully described by the radially dependent function, <math>~\Theta_H(\xi) = [\rho(\xi)/\rho_c]^{1/n}</math>, which is obtained by solving the
Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
As our various discussions illustrate (see the table of contents, below), simply varying the power-law index, <math>~n</math>, gives rise to equilibrium configurations that have a wide variety of internal structural profiles.
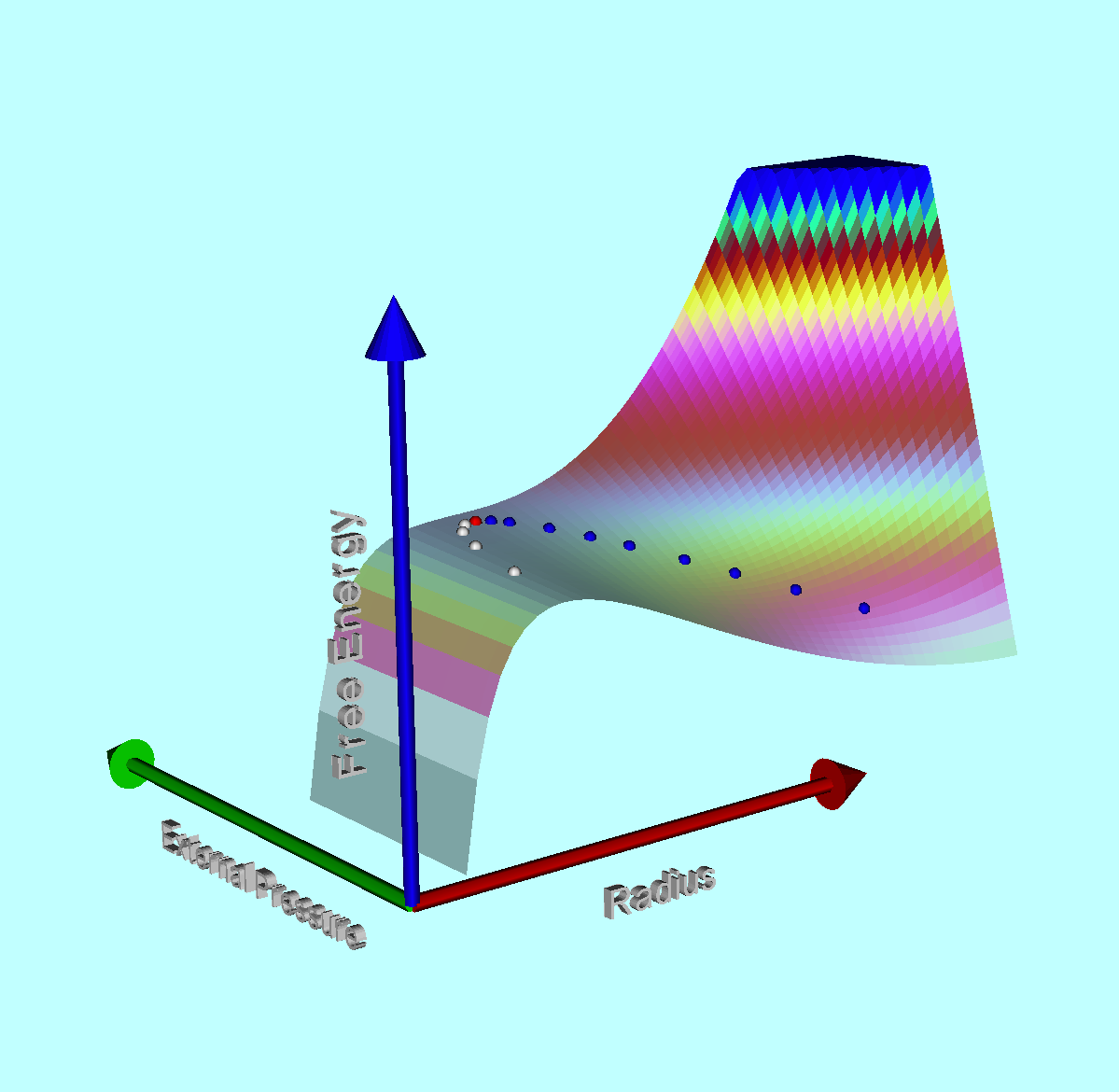
If one is not particularly concerned about details regarding the distribution of matter within the equilibrium configuration, a good estimate of the size of the equilibrium system can be determined by assuming a uniform-density structure then identifying local extrema in the system's global free energy. An illustrative, undulating free-energy surface is displayed here, on the right; blue dots identify equilibria associated with a "valley" of the free-energy surface while white dots identify equilibria that lie along a "ridge" in the free-energy surface.
In the astrophysics community, the mathematical relation that serves to define the properties of configurations that are associated with such free-energy extrema is often referred to as the scalar virial theorem. Specifically, for isolated systems in virial equilibrium, the following relation between configuration parameters holds:
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_A \cdot \mathfrak{f}_M^2}{\mathfrak{f}_W} \, ,</math> |
where all three of the dimensionless structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, are unity, under the assumption that the equilibrium configuration has uniform density and uniform pressure throughout, and are otherwise generically of order unity for detailed force-balanced models having a wide range of internal structures. Alternatively, if the parameter, <math>~K_\mathrm{n}</math> (which defines the specific entropy of fluid elements throughout the configuration), rather than the central pressure, is held fixed while searching for extrema in the free-energy, the virial equilibrium relation for isolated polytropes is,
|
<math>~M^{(n-1)/n} R_\mathrm{eq}^{(3-n)/n} \biggl( \frac{G}{K_\mathrm{n}} \biggr) </math> |
<math>~=</math> |
<math>~\frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggl(\frac{3}{4\pi \mathfrak{f}_M}\biggr)^{1/n} \, . </math> |
Pressure-Truncated Configurations
If the physical system under consideration — such as a protostellar gas cloud — is not isolated but is, instead, surrounded and truncated by a hot, tenuous medium that exerts on the system a confining external pressure, <math>~P_e</math>, the configuration's equilibrium parameters will be related via the expression,
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_M^2}{\mathfrak{f}_W} \biggl[ \mathfrak{f}_A - \frac{P_e}{P_c} \biggr] \, ;</math> |
or, fixing <math>~K_\mathrm{n}</math> instead of <math>~P_c</math>, the relevant virial equilibrium expression is,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K_\mathrm{n} \mathfrak{f}_A \biggl( \frac{3M}{4\pi R_\mathrm{eq}^3} \cdot \frac{1}{\mathfrak{f}_M} \biggr)^{1 + 1/n} - \frac{\mathfrak{f}_W}{5} \biggl(\frac{3GM^2}{4\pi R_\mathrm{eq}^4} \cdot \frac{1}{\mathfrak{f}_M^2} \biggr) \, .</math> |
It is a virial expression specifically of this form <math>~(</math>with <math>n = \infty</math> and <math>\mathfrak{f}_M = \mathfrak{f}_W = \mathfrak{f}_A = 1)</math> that identifies extrema (e.g., valleys or ridges) in the rainbow-colored free-energy surface, <math>\mathfrak{G}^*(R_\mathrm{eq}, P_e)</math>, displayed above. As can be determined from this algebraic expression and as the figure illustrates, for any specified mass no equilibrium states exist if <math>~P_e</math> is greater than some limiting value, <math>~P_\mathrm{crit}</math>; the equilibrium configuration associated with the limiting condition, <math>~P_e = P_\mathrm{crit}</math>, is marked by a red dot on the above-displayed free-energy surface. The astrophysical significance of this critical state was first discussed in the mid 1950s in the context of star formation and, specifically, Bonnor-Ebert spheres.
After rearranging terms, for any specified values of the parameters <math>~P_e</math> and <math>~K_\mathrm{n}</math>, this virial equilibrium expression can also be viewed as a mass-radius relation of the form,
|
<math>~a R_\mathrm{eq}^4 - b M^{(n+1)/n} R_\mathrm{eq}^{(n-3)/n} + c M^2</math> |
<math>~=</math> |
<math>~ 0\, ,</math> |
where the constants,
<math>~a \equiv \frac{4\pi}{3} \cdot P_e \, ,</math> <math>~b \equiv \biggl( \frac{3}{4\pi} \biggr)^{1/n} \cdot K_\mathrm{n} \mathfrak{f}_A \mathfrak{f}_M^{-(n+1)/n} \, ,</math> and <math>~c \equiv \frac{G\mathfrak{f}_W}{5\mathfrak{f}_M^2} \, .</math>
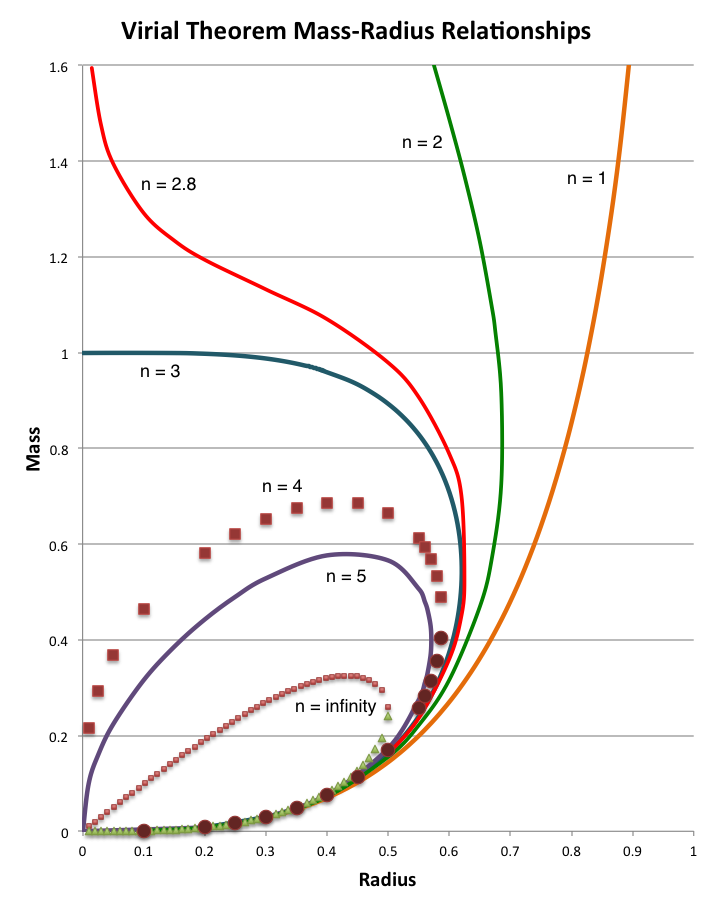
Using this virial equilibrium relation (and, for illustration purposes, assuming a = b = c = 1), the curves drawn in the figure that is displayed here, on the right, show how the equilibrium radius of an embedded, pressure-truncated polytropic sphere varies with mass for seven different adopted polytropic indexes. In direct analogy with the critical pressure that is associated with Bonnor-Ebert spheres, for systems having <math>~n \ge 3</math>, there is a mass, <math>~M_\mathrm{max}</math>, above which equilibrium configurations do not exist; and, when <math>~n > 3</math>, multiple equilibrium configurations having different radii can be constructed for any system having a mass, <math>~M < M_\mathrm{max}</math>.
A detailed force-balance analysis of the structure of embedded, pressure-truncated polytropic configurations reveals, for each choice of <math>~n</math>, a mass-radius relationship that is qualitatively similar to the one deduced from a virial equilibrium analysis. However, the resulting mass-radius relationship is invariably different in detail and quantitatively more correct than the one prescribed by the virial theorem. At its foundation are models whose internal structural profile — of, for example, the fluid pressure and fluid density — is not uniform but, rather, is precisely that which is required to achieve detailed force balance throughout. Hence, we appreciate that even as <math>~P_e</math> and <math>~K_\mathrm{n}</math> are held fixed, in essence the structural form factors must vary from model to model along the more precise "detailed force-balanced" equilibrium sequence.
Bipolytropic Configurations
Additional insight into the structural properties and evolution of stars can be gained by studying bipolytropes — also sometimes referred to as composite polytropes. These are models in which the configuration's "core" is described by a polytropic equation of state having one index — say, <math>~n_c</math> — and the configuration's "envelope" is described by a polytropic equation of state of a different index — say, <math>~n_e</math>. We have found it particularly instructive to examine bipolytropes having <math>~(n_c, n_e) = (5, 1)\, ,</math> in part, because equilibrium models of such systems can be completely described analytically whether they are constructed via a detailed force-balance analysis or by identifying extrema in the free-energy function, that is, via a virial theorem analysis.
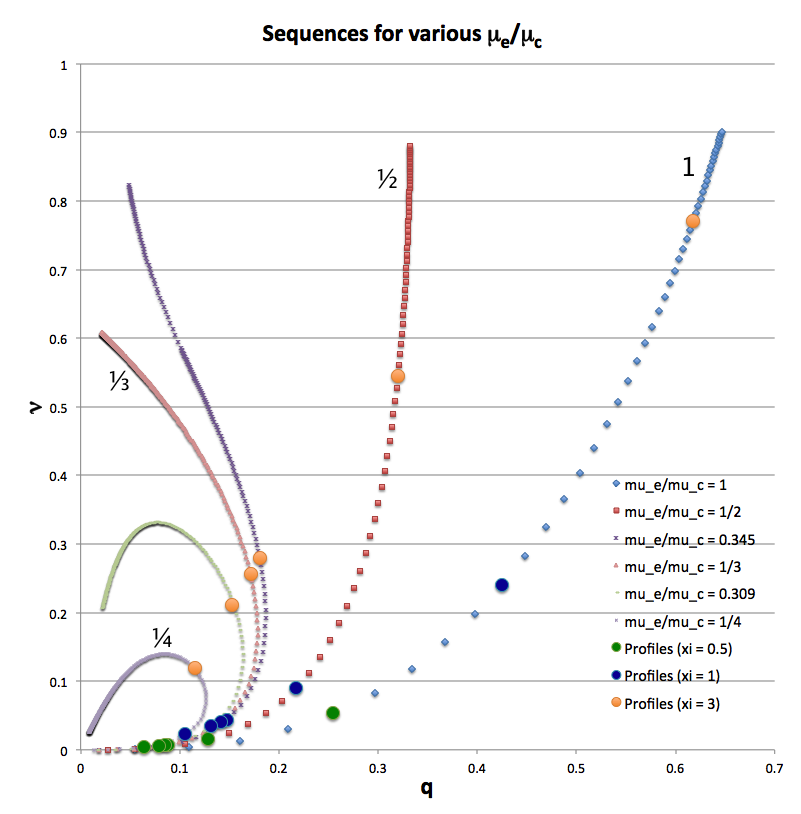
Following the lead of Schönberg & Chandrasekhar (1942) — see, also, Eggleton, Faulkner, and Cannon (1998) — we have pieced these bipolytropic configurations together mathematically in such a way that the mean molecular weight, <math>~\bar{\mu}</math>, of the fluid is allowed to change in a discontinuous fashion at the core-envelope interface. As is illustrated in the figure, shown here on the right, a physically interesting equilibrium model "sequence" can be constructed by monotonically shifting the location of the core-envelope interface from the center of the configuration to its surface while holding fixed the value of the envelope-to-core mean molecular weight ratio, <math>~\mu_e/\mu_c</math>. Each curve shows how the relative mass of the core, <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, correlates with the relative size of the core, as measured by the ratio of the radial position of the core-envelope interface to the equilibrium radius of the composite polytropic configuration, <math>~q \equiv r_i/R_\mathrm{eq}</math>. As the figure illustrates, if the jump in the mean molecular weight is sufficiently extreme — specifically, if <math>~\mu_e/\mu_c < 1/3</math> for the bipolytropic configurations being considered here — there is a core mass, <math>~\nu_\mathrm{max}</math>, above which equilibrium configurations do not exist; and, two equilibrium configurations having different core sizes, <math>~q</math>, can be constructed for any system having a core mass, <math>~\nu < \nu_\mathrm{max}</math>. The astrophysical significance of <math>~\nu_\mathrm{max}</math> was first identified in the early 1940s in bipolytropic configurations having <math>~(n_c, n_e) = (\infty, 3/2)</math>, and has been discussed extensively in the context of the evolutionary transition of stars from the main sequence to the giant branch. It is usually referred to as the Schönberg-Chandrasekhar mass limit.
Details
In the following table, each green check mark identifies and provides a link to an H_Book chapter that presents a detailed discussion of the topic that is identified on the left — for example, the equilibirum structure of "isolated polytropes" or an "isothermal sphere embedded in an external medium." Mathematical models that provide full solutions to the PGEs, including details regarding the internal structural profiles of equilibrium configurations, are derived in chapters whose check marks fall under the column labeled "Detailed Force-Balance." Insight into the properties of equilibrium systems that is revealed via an analysis of a system's free-energy and the corresponding scalar virial theorem is presented in chapters whose check marks fall under the column labeled "Virial Equilibrium." Motivated by a striking similarity between the sets of model sequences displayed in the two "mass-radius" diagrams shown, above, a link also is provided to a chapter that discusses the relationship between the limiting mass associated with Bonnor-Ebert spheres and the Schönberg-Chandrasekhar mass limit.
|
Solution Strategies: |
Detailed Force-Balance |
Virial Equilibrium |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |