Difference between revisions of "User:Tohline/SSC/Virial/PolytropesEmbeddedOutline"
(→Stability: Modify some wording) |
(→Overview: Few minor wording changes) |
||
| Line 24: | Line 24: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{G} | <math>~\mathfrak{G}(x)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 44: | Line 44: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{d\mathfrak{G} | <math>~\frac{d\mathfrak{G}}{dx}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 78: | Line 78: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{d^2\mathfrak{G} | <math>~\frac{d^2\mathfrak{G}}{dx^2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 95: | Line 95: | ||
===Equilibrium Configurations=== | ===Equilibrium Configurations=== | ||
The size, <math>~x_\mathrm{eq}</math>, of each equilibrium configuration is determined by setting, <math>d\mathfrak{G} | The size, <math>~x_\mathrm{eq}</math>, of each equilibrium configuration is determined by setting, <math>d\mathfrak{G}/dx = 0</math>. Hence, <math>~x_\mathrm{eq}</math> is given by the root(s) of the polynomial expression, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5"> | <table border="0" cellpadding="5"> | ||
| Line 114: | Line 114: | ||
</table> | </table> | ||
</div> | </div> | ||
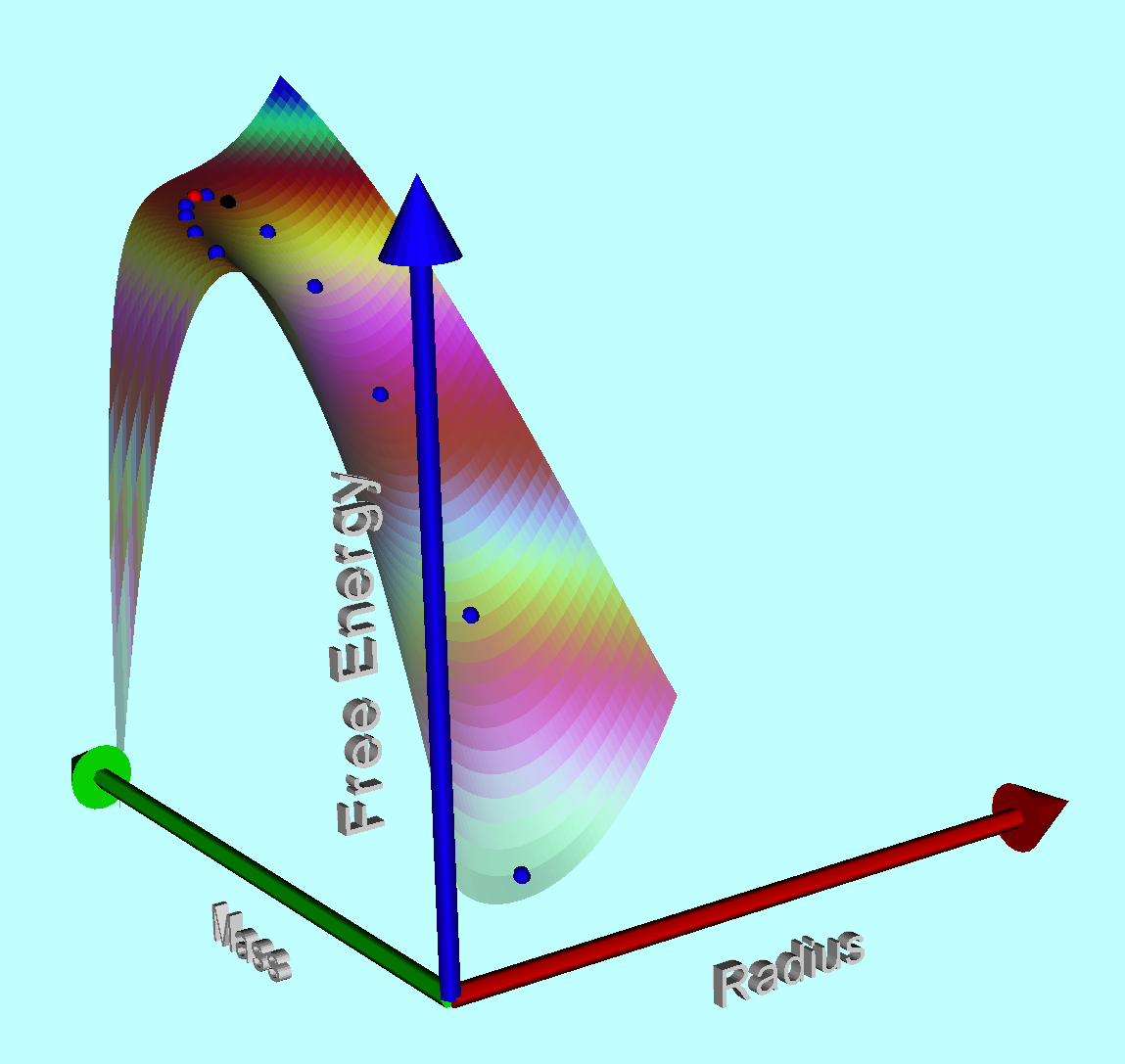
The equilibrium radii of <math>~n = 5</math> polytropic configurations having a variety of different masses are identified by the sequence of a dozen, small colored | (The equilibrium radii of <math>~n = 5</math> polytropic configurations having a variety of different masses are identified by the sequence of a dozen, small colored spherical dots in the above figure.) | ||
===Stability=== | ===Stability=== | ||
The relative stability of each equilibrium configuration is determined by the sign of the second derivative of the free-energy function, evaluated at the specified equilibrium radius. Specifically, the systems being considered here are stable if the second derivative is positive, but they are unstable if the second derivative is negative. | The relative stability of each equilibrium configuration is determined by the sign of the second derivative of the free-energy function, evaluated at the specified equilibrium radius. Specifically, the systems being considered here are stable if the second derivative is positive, but they are unstable if the second derivative is negative. Evaluating the second derivative in this manner gives, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5"> | <table border="0" cellpadding="5"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[ x^{3} \cdot \frac{d^2\mathfrak{G} | <math>~\biggl[ x^{3} \cdot \frac{d^2\mathfrak{G}}{dx^2}\biggr]_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 182: | Line 182: | ||
</table> | </table> | ||
</div> | </div> | ||
(The red | (The small red spherical dot in the above figure identifies the equilibrium configuration at <math>~x_\mathrm{crit} </math>.) We conclude, therefore, that pressure-truncated, equilibrium polytropic configurations having <math>~n > 3</math> are stable if, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5"> | <table border="0" cellpadding="5"> | ||
Revision as of 19:20, 6 February 2015
Virial Equilibrium of Embedded Polytropic Spheres
Overview
The free-energy function that is relevant to a discussion of the structure and stability of a pressure-truncated configuration having polytropic index, <math>~n</math>, has the form,
|
<math>~\mathfrak{G}(x)</math> |
<math>~=</math> |
<math> -ax^{-1} +b x^{-3/n} + c x^3 \, , </math> |
where <math>~x</math> identifies the size of the configuration. (As is explained more fully, below, the above figure displays a free-energy surface of this form for the case, <math>~n=5</math>.) If the coefficients, <math>~a, b</math>, and <math>~c</math>, are held constant while varying the configuration's size, we see that,
|
<math>~\frac{d\mathfrak{G}}{dx}</math> |
<math>~=</math> |
<math> ax^{-2} - \frac{3b}{n}\cdot x^{-(3+n)/n} + 3c x^2 </math> |
|
|
<math>~=</math> |
<math> x^{-2} \biggl[ a - \frac{3b}{n}\cdot x^{(n-3)/n} + 3c x^4 \biggr] \, , </math> |
and,
|
<math>~\frac{d^2\mathfrak{G}}{dx^2}</math> |
<math>~=</math> |
<math> x^{-3} \biggl[ -2a + \frac{3(3+n)b}{n^2}\cdot x^{(n-3)/n} + 6c x^4 \biggr] \, . </math> |
Equilibrium Configurations
The size, <math>~x_\mathrm{eq}</math>, of each equilibrium configuration is determined by setting, <math>d\mathfrak{G}/dx = 0</math>. Hence, <math>~x_\mathrm{eq}</math> is given by the root(s) of the polynomial expression,
|
<math>~x^{(n-3)/n}_\mathrm{eq} </math> |
<math>~=</math> |
<math> \frac{na}{3b} + \frac{nc}{b}\cdot x^4_\mathrm{eq} \, . </math> |
(The equilibrium radii of <math>~n = 5</math> polytropic configurations having a variety of different masses are identified by the sequence of a dozen, small colored spherical dots in the above figure.)
Stability
The relative stability of each equilibrium configuration is determined by the sign of the second derivative of the free-energy function, evaluated at the specified equilibrium radius. Specifically, the systems being considered here are stable if the second derivative is positive, but they are unstable if the second derivative is negative. Evaluating the second derivative in this manner gives,
|
<math>~\biggl[ x^{3} \cdot \frac{d^2\mathfrak{G}}{dx^2}\biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math> -2a + \frac{3(3+n)b}{n^2} \biggl[ \frac{na}{3b} + \frac{nc}{b}\cdot x^4_\mathrm{eq} \biggr] + 6c x^4_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math> -2a + \frac{(3+n)a}{n} + \frac{3(3+n)c}{n} \cdot x^4_\mathrm{eq} + 6c x^4_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>\frac{9(n+1)c}{n}\cdot x^4_\mathrm{eq} - \frac{a(n-3)}{n} \, . </math> |
Defining <math>~x_\mathrm{crit}</math> as the equilibrium radius at which this function goes to zero gives,
|
<math>~x_\mathrm{crit} </math> |
<math>~\equiv</math> |
<math> \biggl[ \frac{a(n-3)}{3^2c(n+1)} \biggr]^{1/4} \, . </math> |
(The small red spherical dot in the above figure identifies the equilibrium configuration at <math>~x_\mathrm{crit} </math>.) We conclude, therefore, that pressure-truncated, equilibrium polytropic configurations having <math>~n > 3</math> are stable if,
|
<math>~x_\mathrm{eq}</math> |
<math>~></math> |
<math> ~x_\mathrm{crit} \, , </math> |
while they are unstable if,
|
<math>~x_\mathrm{eq}</math> |
<math>~<</math> |
<math> ~x_\mathrm{crit} \, . </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Outline of Detailed Investigations Leading to Above Summary
First Effort
My first attempt to analytically define the free energy, and then the virial equilibrium, of pressure-truncated (embedded) polytropic spheres was developed as a direct extension of my description of the virial equilibrium of isolated polytropes. An important outcome of this "first effort" was the unveiling of analytic expressions for the key structural form factors, both for isolated polytropes and, separately, for pressure-truncated polytropic structures.
I am very confident that the form-factor expressions presented for isolated polytropes are all correct because they have been cross-checked with expressions for closely related "integral" parameters discussed by Chandrasekhar [C67]. Although the form-factor expressions derived for pressure-truncated polytropes make some sense — they look very similar to the ones presented for isolated polytropes and seem to behave properly for models which, based on detailed force-balanced analysis, are known to be in equilibrium — I have much less confidence that they are correct. A couple of strategies were developed in an effort to demonstrate the validity and utility of these more general form-factor expressions, resulting in the derivation of a concise virial equilibrium relation,
<math>\Pi_\mathrm{ad} = \chi_\mathrm{ad}^{-3\gamma} - \chi_\mathrm{ad}^{-4} \, ,</math>
that incorporates the newly defined normalization parameters, <math>~R_\mathrm{ad}</math> and <math>~P_\mathrm{ad}</math>. But subsequent derivations aimed at more conclusively demonstrating the correctness of the more general form-factor expressions were messy and got bogged down.
Second Effort
My second attempt to analytically define the free energy, and then the virial equilibrium, of pressure-truncated (embedded) polytropic spheres built upon my first effort and, for a couple of different polytropic indexes, focused on comparing the mass-radius relationship embodied in detailed force-balanced models against the mass-radius relationship implied by the virial theorem. A lot of reasonable results seem to have arisen from a discussion of models (done numerically using Excel) with <math>~n=4</math> polytropic index. And there are some nice aspects of models with an <math>~n=5</math> index, but these models raise some serious concerns related to the fact that two of our "derived" form-factor expressions involve division by the factor, <math>~(5-n)</math>, that is, division by zero.
Third Effort
In an attempt to answer the serious concern(s) raised during our first two efforts, we finally buckled down and performed the integrals necessary to determine expressions for key structural form factors in the cases where the internal structure is known analytically, specifically, for indexes <math>~n=5</math> and <math>~n=1</math>. The result is that the individual expressions derived by direct integration for <math>~\mathfrak{f}_W</math> and for <math>~\mathfrak{f}_A</math> do not match the general form-factor expressions that were rather cavalierly "derived" during our first effort. Oddly enough, as we discovered while fiddling around with the new results, the ratio of these form factors appears to be the same as before, namely,
|
<math>~\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_A - \tilde\theta^{n+1}}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3\cdot 5}{(n+1) \tilde\xi^2 } \biggr] \, . </math> |
It is worth noting that, as a result of this more thorough "third effort" examination, we have confirmed that the third key form factor,
<math>~\mathfrak{f}_M = \frac{\bar\rho}{\rho_c} = \biggl[- \frac{3\tilde\theta^'}{\tilde\xi}\biggr] \, ,</math>
which is the same as before and the same as for isolated polytropes. We also have determined that,
<math>~\biggl(\frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} = \biggl(\frac{\tilde\xi^2 \tilde\theta^'}{\xi_1 \theta^'_1} \biggr)\biggl[- \frac{\tilde\xi}{3\tilde\theta^'}\biggr] = - \frac{\tilde\xi^3 }{3\xi_1 \theta^'_1} \, , </math>
except in the case of <math>~n=5</math> structures, for which we have determined,
<math>~\biggl[\biggl(\frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_{n=5} = \ell^3 = \biggl( \frac{\tilde\xi^2}{3} \biggr)^{3/2} \, . </math>
First Effort, Second Time Around
In an accompanying chapter, we reproduce the discussion associated with our "First Effort", as referenced above, but correct expressions for <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, as identified in our "Third Effort" and, accordingly, re-derive various affected expressions that follow.
Second Effort, Second Time Around
In an accompanying chapter, we reproduce the discussion associated with our "Second Effort", as referenced above, but revise key sections to incorporate corrected expressions for the structural form factors.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |