User:Tohline/SSC/Stability/BiPolytrope0 0Details
Radial Oscillations of a Zero-Zero Bipolytrope
IMPORTANT NOTE! While the overall development in this chapter is correct and, in particular, the chronology of discovery is properly reflected, the final quantitative results — for example, the recorded root(s) of the governing quartic equation — are incorrect because, beginning in the Example21 subsection, below, we started using an incorrect expression for the function <math>~g^2</math>. In an accompanying summary presentation, we have corrected this mistake.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Groundwork
In an accompanying discussion, we derived the so-called,
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. According to our accompanying derivation, if the initial, unperturbed equilibrium configuration is an <math>~(n_c, n_e) = (0,0)</math> bipolytrope, then we know that the relevant functional profiles are as follows for the core and envelope, separately. Note that, throughout, we will preferentially adopt as the dimensionless radial coordinate, the parameter,
|
<math>~\xi</math> |
<math>~\equiv</math> |
<math>~\frac{r}{r_i} \, ,</math> |
in which case,
|
<math>~\chi</math> |
<math>~=</math> |
<math>~ \chi_i \xi = q \biggl( \frac{G\rho_c^2 R^2}{P_c} \biggr)^{1 /2 }\xi \, .</math> |
The corresponding radial coordinate range is,
<math>~0 \le \xi \le 1 </math> for the core, and
<math>~1 \le \xi \le \frac{1}{q} </math> for the envelope.
Core
|
<math>~r_0</math> |
<math>~=</math> |
<math>~\biggl( \frac{P_c}{G\rho_c^2}\biggr)^{1 / 2} \chi = (qR) \xi \, ,</math> |
|
<math>~\rho_0</math> |
<math>~=</math> |
<math>~\rho_c \, ,</math> |
|
<math>~\frac{P_0}{P_c}</math> |
<math>~=</math> |
<math>~1 - \frac{2\pi}{3} \chi^2 = 1 - \frac{2\pi}{3} \biggl[ \frac{G\rho_c^2 R^2}{P_c} \biggr] q^2 \xi^2 = 1 - \frac{\xi^2}{g^2} \, ,</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3} \biggl( \frac{P_c^3}{G^3 \rho_c^4} \biggr)^{1 / 2}\chi^3 = \frac{4\pi}{3} \biggl( \frac{P_c^3}{G^3 \rho_c^4} \biggr)^{1 / 2} \biggl( \frac{G\rho_c^2 R^2}{P_c} \biggr)^{3 /2 } (q\xi)^3 </math> |
|
|
<math>~=</math> |
<math>~ \frac{4\pi}{3} ( \rho_c R^3 ) (q\xi)^3 = \frac{4\pi}{3} (q\xi)^3 \rho_c \biggl[ \biggl( \frac{P_c}{G\rho_c^2} \biggr)^{1 / 2} \biggl( \frac{3}{2\pi} \biggr)^{1 / 2} \frac{1}{qg}\biggr]^3 </math> |
|
|
<math>~=</math> |
<math>~ \frac{4\pi}{3} (q\xi)^3 \biggl[ \biggl( \frac{P_c^3}{G^3\rho_c^4} \biggr)^{1 / 2} \biggl( \frac{3}{2\pi} \biggr)^{3 / 2} \frac{1}{q^3g^3}\biggr] = \frac{4\pi}{3} \biggl[ \biggl(\frac{\pi}{6}\biggr)^{1 / 2} \nu g^3 M_\mathrm{tot} \biggl( \frac{3}{2\pi} \biggr)^{3 / 2} \frac{1}{g^3}\biggr]\xi^3 </math> |
|
|
<math>~=</math> |
<math>~ M_\mathrm{tot} \nu \xi^3 \, , </math> |
where,
|
<math>~g^2(\nu,q)</math> |
<math>~\equiv</math> |
<math> \biggl\{ 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \biggr\} \, , </math> |
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math> \frac{q^3}{\nu} \biggl( \frac{1-\nu}{1-q^3}\biggr) \, . </math> |
Hence,
|
<math>~g_0</math> |
<math>~=</math> |
<math>~\frac{G(M_\mathrm{tot} \nu \xi^3)}{(qR\xi)^2} = \biggl( \frac{GM_\mathrm{tot} }{R^2 } \biggr) \frac{\nu \xi}{q^2} </math> |
|
|
<math>~=</math> |
<math>~ G \biggl[\biggl( \frac{P_c^3}{G^3\rho_c^4} \biggr)^{1 / 2} \biggl(\frac{6}{\pi}\biggr)^{1 / 2} \frac{1}{\nu g^3} \biggr] \biggl[\biggl(\frac{G\rho_c^2}{P_c} \biggr)^{ 1 / 2} \biggl(\frac{2\pi}{3} \biggr)^{1 / 2} qg \biggr]^2 \frac{\nu \xi}{q^2} </math> |
|
|
<math>~=</math> |
<math>~ (P_c G)^{1 / 2} \biggl(\frac{2^3\pi}{3} \biggr)^{1 / 2} \frac{\xi}{g} </math> |
|
<math>~\frac{\rho_0}{P_0}</math> |
<math>~=</math> |
<math>~ \frac{\rho_c}{P_c} \biggl[ 1 - \frac{\xi^2}{g^2} \biggr]^{-1} = \frac{\rho_c}{P_c} \biggl( \frac{g^2}{g^2 - \xi^2} \biggr) \, ;</math> |
and the wave equation for the core becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{1}{(qR)^2} \cdot \frac{d^2x}{d\xi^2} + \biggl[\frac{4qR}{r_0} - \biggl(\frac{qR g_0 \rho_0}{P_0}\biggr) \biggr] \frac{1}{(qR)^2} \cdot \frac{dx}{d\xi} + \biggl(\frac{\rho_0}{P_0} \biggr)\biggl[ \frac{\omega^2}{\gamma_\mathrm{g} } + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr)\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(qR)^2} \biggl\{ \frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - q\biggl(\frac{P_c}{G\rho_c^2} \biggr)^{1 / 2}\biggl(\frac{3}{2\pi}\biggr)^{1 / 2} \frac{1}{qg} (P_c G)^{1 / 2} \biggl(\frac{2^3\pi}{3} \biggr)^{1 / 2} \frac{\xi}{g} \frac{\rho_c}{P_c} \biggl( \frac{g^2}{g^2 - \xi^2} \biggr) \biggr] \frac{dx}{d\xi} \biggr\} </math> |
|
|
|
<math>~ + \frac{\rho_c}{P_c} \biggl( \frac{g^2}{g^2 - \xi^2} \biggr) \biggl[ \frac{\omega^2}{\gamma_\mathrm{g} } + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr)(P_c G)^{1 / 2} \biggl(\frac{2^3\pi}{3} \biggr)^{1 / 2} \frac{\xi}{g} \cdot \frac{1}{qR\xi}\biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(qR)^2} \biggl\{ \frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \biggl( \frac{2\xi}{g^2 - \xi^2} \biggr) \biggr] \frac{dx}{d\xi} \biggr\} </math> |
|
|
|
<math>~ + \frac{\rho_c}{P_c} \biggl( \frac{g^2}{g^2 - \xi^2} \biggr) \biggl[ \frac{\omega^2}{\gamma_\mathrm{g} } + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr)(P_c G)^{1 / 2} \biggl(\frac{2^3\pi}{3} \biggr)^{1 / 2} \frac{1}{qg} \biggl(\frac{G\rho_c^2}{P_c} \biggr)^{1 / 2} \biggl( \frac{2\pi}{3} \biggr)^{1 / 2} qg \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(qR)^2(g^2 - \xi^2)} \biggl\{ (g^2 - \xi^2)\frac{d^2x}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \frac{q^2 g^2 R^2 \rho_c}{P_c} \biggl[ \frac{\omega^2}{\gamma_\mathrm{g} } + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr) \frac{4\pi G\rho_c}{3} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{(qR)^2(g^2 - \xi^2)} \biggl\{ (g^2 - \xi^2)\frac{d^2x}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + 2\biggl[ \frac{3\omega^2}{\gamma_\mathrm{g}4\pi G\rho_c} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr) \biggr] x \biggr\} \, . </math> |
Envelope
|
<math>~r_0</math> |
<math>~=</math> |
<math>~ (qR) \xi \, ,</math> |
|
<math>~\rho_0</math> |
<math>~=</math> |
<math>~\rho_e \, ,</math> |
|
<math>~\frac{P_0}{P_c}</math> |
<math>~=</math> |
<math> 1 - \frac{2\pi}{3}\chi_i^2 + \frac{2\pi}{3} \biggl(\frac{\rho_e}{\rho_c}\biggr) \chi_i^2 \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{1}{\xi} - 1\biggr) - \frac{\rho_e}{\rho_c} (\xi^2 - 1) \biggr] </math> |
|
|
<math>~=</math> |
<math> 1 - \frac{1}{g^2}\biggl\{ 1 - \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{1}{\xi} - 1\biggr) - \frac{\rho_e}{\rho_c} (\xi^2 - 1) \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{g^2 P_0}{P_c}</math> |
<math>~=</math> |
<math> g^2 - 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{1}{\xi} - 1\biggr) - \frac{\rho_e}{\rho_c} (\xi^2 - 1) \biggr] \, , </math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>\frac{4\pi}{3} \biggl[ \frac{P_c^3}{G^3 \rho_c^4} \biggr]^{1/2} \chi_i^3\biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr]</math> |
|
|
<math>~=</math> |
<math>M_\mathrm{tot} \frac{4\pi}{3} \biggl[\biggl( \frac{\pi}{6}\biggr)^{1 / 2}\nu g^3 \biggr] \biggl[ \biggr(\frac{3}{2\pi}\biggr)\frac{1}{g^2} \biggr]^{3 /2} \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math> \nu M_\mathrm{tot} \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] \, . </math> |
Hence,
|
<math>~g_0</math> |
<math>~=</math> |
<math>~ \frac{G M_\mathrm{tot}\nu }{ R^2 q^2\xi^2} \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] \, , </math> |
and, after multiplying through by <math>~(q^2 R^2 g^2P_0/P_c)</math>, the wave equation for the envelope becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\frac{q^2 g^2 R^2 P_0}{P_c} \biggl\{ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} \biggr\} + \frac{q^2 g^2 R^2 \rho_0}{P_c} \biggl[ \frac{\omega^2 }{\gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr)\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~\frac{g^2 P_0}{P_c} \biggl\{ \frac{d^2x}{d\xi^2} + \biggl[4 - \biggl(\frac{qRg_0 \rho_e}{P_0}\biggr) \xi\biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} \biggr\} + \frac{q^2 g^2 R^2 \rho_e}{P_c} \biggl[ \frac{\omega^2 }{\gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr)\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - \biggl(\frac{qg^2Rg_0 \rho_e}{P_c}\biggr) \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \frac{3}{4\pi G \rho_c} \biggl\{ \frac{\omega^2 }{\gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr)\biggl(\frac{4\pi G \rho_c}{3}\biggr) \biggl[ \frac{1}{\xi^3} + \frac{\rho_e}{\rho_c}\biggl(1-\frac{1}{\xi^3}\biggr) \biggr] \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2 \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl\{ \frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr) \biggl[ \frac{1}{\xi^3} + \frac{\rho_e}{\rho_c}\biggl(1-\frac{1}{\xi^3}\biggr) \biggr] \biggr\} x </math> |
Check1
If <math>~\rho_e/\rho_c = 1</math>, this envelope wave equation should match seamlessly into the core wave equation. Let's see if it does. First,
|
<math>~g^2(\nu,q)|_{\rho_e=\rho_c}</math> |
<math>~=</math> |
<math> 1 + \biggl(\frac{1}{q^2} - 1\biggr) =\frac{1}{q^2} \, , </math> |
|
<math>~\frac{g^2 P_0}{P_c} \biggr|_{\rho_e = \rho_c}</math> |
<math>~=</math> |
<math>~ g^2 - \xi^2 = \frac{1}{q^2} - \xi^2 \, . </math> |
Hence, for the envelope,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2 \biggl[1 + \biggl( \xi^3 - 1\biggr) \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + 2 \biggl\{ \frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr) \biggl[ \frac{1}{\xi^3} + \biggl(1-\frac{1}{\xi^3}\biggr) \biggr] \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{1}{q^2} - \xi^2 \biggr) \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2\xi \cdot \frac{dx}{d\xi} + 2 \biggl\{ \frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr) \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{1}{q^2} - \xi^2 \biggr) \frac{d^2x}{d\xi^2} + \biggl\{ 4\biggl( \frac{1}{q^2} - \xi^2 \biggr) - 2\xi^2 \biggr\} \frac{1}{\xi} \cdot \frac{dx}{d\xi} + 2 \biggl[ \frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr) \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{1}{q^2} - \xi^2 \biggr) \frac{d^2x}{d\xi^2} + \biggl( \frac{4}{q^2} - 6\xi^2 \biggr) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + 2 \biggl[ \frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g}} \biggr) \biggr] x \, . </math> |
Whereas, for the core,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl(\frac{1}{q^2} - \xi^2 \biggr)\frac{d^2x}{d\xi^2} + \biggl( \frac{4}{q^2} - 6\xi^2 \biggr) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + 2\biggl[ \frac{3\omega^2}{\gamma_\mathrm{g}4\pi G\rho_c} + \biggl( \frac{4 - 3\gamma_\mathrm{g}}{\gamma_\mathrm{g} } \biggr) \biggr] x \, , </math> |
which matches exactly.
Boundary Condition
In order to ensure finite pressure fluctuations at the surface of this bipolytropic configuration, we need the logarithmic derivative of <math>~x</math> to obey the following relation:
|
<math>~ \frac{d\ln x}{d\ln r_0}\biggr|_\mathrm{surface}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) \, .</math> |
Now, according to our accompanying discussion of the equilibrium mass and radius of a zero-zero polytrope, we know that,
|
<math>~\frac{R^3}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{P_c}{G\rho_c^2}\biggr)^{3 / 2} \biggl( \frac{3}{2\pi}\biggr)^{3 / 2} \frac{1}{(qg)^3} \biggl(\frac{G^3 \rho_c^4}{P_c^3}\bigg)^{1 / 2} \biggl(\frac{\pi}{2\cdot 3}\biggr)^{1 / 2} \nu g^3 </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi \rho_c} \biggr) \frac{\nu}{q^3} \, . </math> |
Hence, a reasonable surface boundary condition is,
|
<math>~ \frac{d\ln x}{d\ln r_0}\biggr|_\mathrm{surface}</math> |
<math>~=</math> |
<math>~\frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} \biggl( \frac{\nu}{q^3}\biggr) - \biggl( 3 - \frac{4}{\gamma_\mathrm{g}}\biggr) \, .</math> |
Attempt to Find Eigenfunction for the Envelope
Adopting some of the notation used by T. E. Sterne (1937) and enunciated in our accompanying discussion of the uniform-density sphere, we'll define,
|
<math>~\alpha</math> |
<math>~\equiv</math> |
<math>~3 - 4/\gamma_\mathrm{g} \, ,</math> |
|
<math>~\mathfrak{F}</math> |
<math>~\equiv</math> |
<math>~\frac{3\omega^2 }{2\pi \gamma_\mathrm{g} G \rho_c} - 2 \alpha \, ,</math> |
in which case the wave equation for the core becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{1}{(qR)^2(g^2 - \xi^2)} \biggl\{ (g^2 - \xi^2)\frac{d^2x}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \mathfrak{F} x \biggr\} \, , </math> |
and the wave equation for the envelope becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2 \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl\{ \mathfrak{F} + 2\alpha \biggl[1 - \frac{1}{\xi^3} - \frac{\rho_e}{\rho_c}\biggl(1-\frac{1}{\xi^3}\biggr) \biggr] \biggr\} x \, . </math> |
A Specific Choice of the Density Ratio
Now, let's focus on the specific model for which <math>~\rho_e/\rho_c = 1/2</math>. In this case,
|
<math>~g^2(\nu,q) \biggr|_{\rho_e/\rho_c=1/2}</math> |
<math>~=</math> |
<math> 1 + \frac{1}{2} \biggl[ 1-q + \frac{1}{2} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>\frac{1}{4q^2}\biggl\{ 4q^2 + \biggl[ 2q^2 - 2q^3 + 1-q^2 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1+5q^2 - 2q^3 }{4q^2} \biggr] \, ; </math> |
|
<math>~\frac{g^2 P_0}{P_c}\biggr|_{\rho_e/\rho_c=1/2}</math> |
<math>~=</math> |
<math> g^2 - 1 + \frac{1}{2} \biggl[ \biggl( \frac{1}{\xi} - 1\biggr) - \frac{1}{2} \biggl(\xi^2 - 1 \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math> g^2 - 1 - \frac{1}{4} \biggl[ \xi^2 + 1 - \frac{2}{\xi} \biggr] </math> |
|
|
<math>~=</math> |
<math> g^2 - \frac{\xi^2}{4} \biggl[ 1 + \frac{5}{\xi^2} - \frac{2}{\xi^3} \biggr] \, . </math> |
Note that this last expression goes to zero at the surface of the bipolytrope, that is, at <math>~\xi = 1/q</math>. For this specific case, the wave equation for the envelope becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - \biggl[1 +\frac{1}{2} \biggl( \xi^3 - 1\biggr) \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} + \frac{1}{2} \biggl\{ \mathfrak{F} + 2\alpha \biggl[1 - \frac{1}{\xi^3} + \frac{1}{2}\biggl(-1 + \frac{1}{\xi^3}\biggr) \biggr] \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ g^2 - \frac{\xi^2}{4} \biggl[ 1 + \frac{5}{\xi^2} - \frac{2}{\xi^3} \biggr] \biggr\} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - \frac{1}{2}\biggl[1 + \xi^3 \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} + \frac{1}{2} \biggl\{ \mathfrak{F} + \alpha \biggl[1 - \frac{1}{\xi^3} \biggr] \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\xi^3} \biggl\{ \biggl[ 4g^2\xi^3 - \xi^5 \biggl( 1 + \frac{5}{\xi^2} - \frac{2}{\xi^3} \biggr) \biggr] \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2\xi (1 + \xi^3 ) \frac{dx}{d\xi} + 2 \xi^3 \biggl[ \mathfrak{F} + \alpha \biggl(1 - \frac{1}{\xi^3} \biggr) \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\xi^3} \biggl\{ \biggl[ 4g^2\xi^3 - \xi^5 - 5\xi^3 + 2\xi^2 \biggr] \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2\xi (1 + \xi^3 ) \frac{dx}{d\xi} + \biggl[ 2 \xi^3 (\mathfrak{F} + \alpha) - 2\alpha \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\xi^3} \biggl\{ \biggl[ 2 + (4g^2 - 5)\xi - \xi^3 \biggr] \biggl[ \xi^2 \cdot \frac{d^2x}{d\xi^2} + 4\xi \cdot \frac{dx}{d\xi} \biggr] - 2(1 + \xi^3 ) \biggl[ \xi \cdot \frac{dx}{d\xi} \biggr] - \biggl[ 2\alpha - 2 \xi^3 (\mathfrak{F} + \alpha) \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\xi^3} \biggl\{ \biggl[ 2 + (4g^2 - 5)\xi - \xi^3 \biggr] \biggl[ \xi^2 \cdot \frac{d^2x}{d\xi^2} \biggr] +\biggl[ 3 + (8g^2 - 10)\xi - 3\xi^3 \biggr] \biggl[ 2\xi \cdot \frac{dx}{d\xi} \biggr] - \biggl[ 2\alpha - 2 \xi^3 (\mathfrak{F} + \alpha) \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{x}{4\xi^3} \biggl\{ \biggl[ 2 + (4g^2 - 5)\xi - \xi^3 \biggr] \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] +\biggl[ 6 + 4(4g^2 - 5)\xi - 6\xi^3 \biggr] \biggl[ \frac{\xi}{x} \cdot \frac{dx}{d\xi} \biggr] - \biggl[ 2\alpha - 2 \xi^3 (\mathfrak{F} + \alpha) \biggr] \biggr\} \, . </math> |
Idea Involving Logarithmic Derivatives
Notice that the term involving the first derivative of <math>~x</math> can be written as a logarithmic derivative; specifically,
|
<math>~\frac{\xi}{x} \cdot \frac{dx}{d\xi} </math> |
<math>~=</math> |
<math>~\frac{d\ln x}{d\ln \xi} \, .</math> |
Let's look at the second derivative of this quantity.
|
<math>~\frac{d}{d\xi} \biggl[ \frac{d\ln x}{d\ln \xi} \biggr]</math> |
<math>~=</math> |
<math>~ \frac{\xi}{x} \cdot \frac{d^2x}{d\xi^2} + \frac{dx}{d\xi} \cdot \biggl[ \frac{1}{x} - \frac{\xi}{x^2} \cdot \frac{dx}{d\xi}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\xi}{x} \cdot \frac{d^2x}{d\xi^2} + \frac{1}{x} \biggl[ 1 - \frac{d\ln x}{d\ln \xi} \biggr]\cdot \frac{dx}{d\xi} </math> |
|
<math>~\Rightarrow ~~~ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} </math> |
<math>~=</math> |
<math>~ \frac{d}{d\ln\xi} \biggl[ \frac{d\ln x}{d\ln \xi} \biggr] - \biggl[ 1 - \frac{d\ln x}{d\ln \xi} \biggr]\cdot \frac{d\ln x}{d\ln \xi} \, . </math> |
Now, if we assume that the envelope's eigenfunction is a power-law of <math>~\xi</math>, that is, assume that,
<math>~x = a_0 \xi^{c_0} \, ,</math>
then the logarithmic derivative of <math>~x</math> is a constant, namely,
<math>~\frac{d\ln x}{d\ln\xi} = c_0 \, ,</math>
and the two key derivative terms will be,
|
<math>~\frac{\xi}{x} \cdot \frac{dx}{d\xi} = c_0 \, ,</math> |
and |
<math>~\frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} = c_0(c_0-1) \, .</math> |
Hence, in order for the wave equation for the envelope for the specific density ratio being considered here to be satisfied, we need,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[ 2 + (4g^2 - 5)\xi - \xi^3 \biggr] \biggl[ c_0(c_0-1) \biggr] +\biggl[ 6 + 4(4g^2 - 5)\xi - 6\xi^3 \biggr] \biggl[ c_0 \biggr] - \biggl[ 2\alpha - 2 \xi^3 (\mathfrak{F} + \alpha) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ 2 + (4g^2 - 5)\xi - \xi^3 \biggr] c_0(c_0-1) +c_0\biggl[ 6 + 4(4g^2 - 5)\xi - 6\xi^3 \biggr] - \biggl[ 2\alpha - 2 \xi^3 (\mathfrak{F} + \alpha) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[2c_0(c_0-1) + 6c_0 - 2\alpha \biggr] + \biggl[(4g^2-5)(c_0^2 - c_0 + 4c_0 ) \biggr]\xi + \biggl[ -c_0(c_0-1) -6c_0 + 2(\mathfrak{F}+\alpha) \biggr]\xi^3 </math> |
|
|
<math>~=</math> |
<math>~ 2\biggl[c_0^2 + 2c_0 - \alpha \biggr] + \biggl[(4g^2-5)(c_0^2 + 3c_0 ) \biggr]\xi + \biggl[ 2(\mathfrak{F}+\alpha) - c_0(c_0+5) \biggr]\xi^3 \, . </math> |
This means that three algebraic relations must simultaneously be satisfied, namely:
|
<math>~\xi^{0}:</math> |
<math>~c_0^2 + 2c_0 - \alpha =0</math> |
<math>~\Rightarrow~</math> |
<math>~c_0 = -1 \pm (1+\alpha)^{1 / 2} \, ;</math> |
|
<math>~\xi^{1}:</math> |
<math>~g^2 = \frac{5}{4}</math> |
<math>~\Rightarrow~</math> |
<math>~q=\biggl(\frac{1}{2}\biggr)^{1 / 3} </math> and, hence, <math>~\nu = \frac{2}{3} \, ;</math> |
|
<math>~\xi^{3}:</math> |
<math>~2(\mathfrak{F}+\alpha) = c_0(c_0+5)</math> |
<math>~\Rightarrow~</math> |
<math>~\frac{2}{3}\cdot \sigma^2 = (\alpha-1) \pm \sqrt{\alpha+1} \, .</math> |
More General Solution
Leaving the density ratio unspecified, let's try to write the wave equation for the envelope in the same form, and see if the logarithmic derivatives can be manipulated in a similar fashion.
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{g^2 P_0}{P_c} \biggl[ \frac{d^2x}{d\xi^2} + \frac{4}{\xi} \cdot \frac{dx}{d\xi} \biggr] - 2 \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[1 +\frac{\rho_e}{\rho_c} \biggl( \xi^3 - 1\biggr) \biggr] \frac{1}{\xi^2} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl\{ \mathfrak{F} + 2\alpha \biggl[1 - \frac{1}{\xi^3} - \frac{\rho_e}{\rho_c}\biggl(1-\frac{1}{\xi^3}\biggr) \biggr] \biggr\} x </math> |
|
<math>~\Rightarrow ~~~\frac{\xi^3}{x} \cdot 0</math> |
<math>~=</math> |
<math>~ \frac{g^2\xi P_0}{P_c} \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] + \biggl\{ \frac{4g^2 \xi P_0}{P_c} - 2 \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[\biggl( 1-\frac{\rho_e}{\rho_c} \biggr) +\biggl(\frac{\rho_e}{\rho_c} \biggr) \xi^3 \biggr] \biggr\} \frac{\xi}{x} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ +\xi^3 \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl\{ \biggl[ \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr] + 2\alpha\biggl( \frac{\rho_e}{\rho_c} -1\biggr) \cdot \frac{1}{\xi^3} \biggr\} </math> |
where,
|
<math>~\frac{g^2\xi P_0}{P_c}</math> |
<math>~=</math> |
<math> \xi \biggl\{ g^2 - 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{1}{\xi} - 1\biggr) - \frac{\rho_e}{\rho_c} (\xi^2 - 1) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \xi \biggl\{ \biggl[ 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggr] \frac{1}{\xi} +\biggl[ g^2 - 1 - 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) + \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \biggr] - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math> \biggl[ 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggr] +\biggl[ g^2 - 1 - 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) + \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \biggr]\xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 </math> |
|
|
<math>~=</math> |
<math> \biggl[ 2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggr] +\biggl[ g^2 - 1 - 2\biggl(\frac{\rho_e}{\rho_c}\biggr) + 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \biggr]\xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \, . </math> |
Hence, the wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[ \mathcal{A} + (g^2-\mathcal{B}) \xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] + \biggl\{ 4\biggl[ \mathcal{A} + (g^2-\mathcal{B}) \xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] - \mathcal{A} - 2\biggl(\frac{\rho_e}{\rho_c} \biggr)^2 \xi^3 \biggr\} \frac{\xi}{x} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + \biggl[ \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 + 2\alpha\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \frac{\rho_e}{\rho_c} -1\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \mathcal{A} + (g^2-\mathcal{B}) \xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] + \biggl\{ 3\mathcal{A} + 4(g^2-\mathcal{B}) \xi - 6\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \biggr\} \frac{\xi}{x} \cdot \frac{dx}{d\xi} </math> |
|
|
|
<math>~ + \biggl[ \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \mathcal{A} \biggr] \, , </math> |
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \, ; </math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \, . </math> |
As before, if we assume a power-law solution, the wave equation for the envelope becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[ \mathcal{A} + (g^2-\mathcal{B}) \xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \biggl[ c_0(c_0-1) \biggr] + \biggl\{ 3\mathcal{A} + 4(g^2-\mathcal{B}) \xi - 6\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \biggr\} c_0 </math> |
|
|
|
<math>~ + \biggl[ \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \mathcal{A} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\xi^0 \biggl[ \mathcal{A}c_0(c_0-1) + 3\mathcal{A}c_0 -\alpha\mathcal{A} \biggr] + \xi^1 \biggl[ (g^2-\mathcal{B})c_0(c_0-1) +4(g^2-\mathcal{B})c_0 \biggr] + \xi^3 \biggl[\biggl(\frac{\rho_e}{\rho_c}\biggr)^2c_0(1-c_0) - 6\biggl(\frac{\rho_e}{\rho_c}\biggr)^2c_0 +\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\xi^0 \biggl[ c_0(c_0-1) + 3c_0 -\alpha \biggr]\mathcal{A} + \xi^1 \biggl[ (g^2-\mathcal{B})(c_0^2+3c_0)\biggr] + \xi^3 \biggl[( \mathfrak{F} + 2\alpha ) - \biggl(\frac{\rho_e}{\rho_c}\biggr)(5c_0 +c_0^2 + 2\alpha) \biggr]\biggl(\frac{\rho_e}{\rho_c}\biggr) \, .
</math> |
This means that three algebraic relations must simultaneously be satisfied, namely:
|
<math>~\xi^{0}:</math> |
<math>~c_0^2 + 2c_0 - \alpha =0</math> |
<math>~\Rightarrow~</math> |
<math>~c_0 = -1 \pm (1+\alpha)^{1 / 2} \, ;</math> |
|
<math>~\xi^{3}:</math> |
<math>~(\mathfrak{F}+2\alpha) = \biggl(\frac{\rho_e}{\rho_c}\biggr)(5c_0 +c_0^2 + 2\alpha)</math> |
<math>~\Rightarrow~</math> |
<math>~\sigma^2 \equiv \frac{3\omega^2}{2\pi G\rho_c \gamma_\mathrm{g}}= 3\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ (\alpha-1) \pm \sqrt{\alpha+1} \biggr] \, ;</math> |
|
<math>~\xi^{1}:</math> |
<math>~g^2 = 1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2</math> |
<math>~\Rightarrow~</math> |
<math>~q^3 = \frac{(\rho_e/\rho_c)}{2[1-(\rho_e/\rho_c) ]} </math> |
|
|
|
and, hence, |
<math>~\nu = \frac{1}{3[1-(\rho_e/\rho_c) ]} \, .</math> |
Surface Boundary Condition
Given that, with this solution, the ratio,
|
<math>~\frac{\nu}{q^3}</math> |
<math>~=</math> |
<math>~\frac{1}{3[1-(\rho_e/\rho_c) ]} \biggl\{ \frac{2[1-(\rho_e/\rho_c) ]}{(\rho_e/\rho_c)} \biggr\} = \frac{2}{3(\rho_e/\rho_c) } \, ,</math> |
we see that the desired surface boundary condition is,
|
<math>~ \frac{d\ln x}{d\ln r_0}\biggr|_\mathrm{surface}</math> |
<math>~=</math> |
<math>~\frac{3\omega^2 }{4\pi G\rho_c \gamma_\mathrm{g}} \cdot \frac{2}{3(\rho_e/\rho_c) } - \biggl( 3 - \frac{4}{\gamma_\mathrm{g}}\biggr) </math> |
|
|
<math>~=</math> |
<math>~\frac{\sigma^2}{3(\rho_e/\rho_c) } - \alpha </math> |
|
|
<math>~=</math> |
<math>~c_0 \, . </math> |
But, for our identified solution, this is the logarithmic derivative of <math>~x</math> throughout the envelope as well as at the surface. So the boundary condition is automatically satisfied.
Match to a Core Eigenfunction (First Blundering)
If we define,
<math>~\eta \equiv \frac{\xi}{g} \, ,</math>
the above wave equation for the core becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1 - \eta^2)\frac{d^2x}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} + \mathfrak{F} x \, . </math> |
Not surprisingly, this is identical in form to the eigenvalue problem first presented by Sterne (1937) in connection with an examination of radial oscillations in uniform-density spheres. For the core of our zero-zero bipolytrope, we can therefore adopt any one of the polynomial eigenfunctions and corresponding eigenfrequencies derived by Sterne. We will insist that the eigenfrequency of the envelope match the eigenfrequency of the core; and, following J. O. Murphy & R. Fiedler (1985b) (see the top paragraph of the right-hand column on p. 223 of their article), we seek solutions for which there is continuity in both the eigenfunction and its first derivative at the interface <math>~(\xi = 1)</math>.
Try Quadratic Core Eigenfunction
Let's begin with Sterne's quadratic function and see if we can match it to the envelope's power-law eigenfunction. Keeping in mind that the overall normalization is arbitrary, from Sterne's presentation, we have,
|
<math>~x_\mathrm{core}</math> |
<math>~=</math> |
<math>~a\biggl[ 1-\frac{7}{5}\eta^2 \biggr]</math> |
|
|
<math>~=</math> |
<math>~a\biggl[ 1-\frac{7}{5}\biggl( \frac{\xi}{g}\biggr)^2 \biggr] \, ,</math> |
and the associated eigenfrequency is obtained by setting,
<math>~\mathfrak{F} = \sigma^2 - 2\alpha = 14 \, .</math>
In this case, then, the eigenfrequency for the envelope will match the eigenfrequency of the core if,
|
<math>~14 + 2\alpha</math> |
<math>~=</math> |
<math>~ 3\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ (\alpha-1) \pm \sqrt{\alpha+1} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\rho_e}{\rho_c} \biggr) </math> |
<math>~=</math> |
<math>~\frac{2}{3}\cdot \frac{7 + \alpha}{ (\alpha-1) \pm \sqrt{\alpha+1} }</math> |
Now, the eigenfunction for the envelope is,
<math>~x_\mathrm{env} = \xi^{c_0} \, ,</math>
where,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
The value of this function will match the value of its core counterpart at the interface <math>~(\xi=1)</math> if,
|
<math>~a\biggl[ 1-\frac{7}{5}\biggl( \frac{1}{g}\biggr)^2 \biggr]</math> |
<math>~=</math> |
<math>~1</math> |
|
<math>~\Rightarrow ~~~ a</math> |
<math>~=</math> |
<math>~\biggl[ 1-\frac{7}{5}\biggl( \frac{1}{g}\biggr)^2 \biggr]^{-1} \, .</math> |
Finally, the slope (first derivative) of the core eigenfunction will match the slope of the envelope eigenfunction at the interface if,
|
<math>~c_0 \xi^{c_0-1}\biggr|_\mathrm{\xi=1}</math> |
<math>~=</math> |
<math>~ -\frac{14a}{5g^2} \cdot \xi\biggr|_\mathrm{\xi=1} </math> |
|
<math>~\Rightarrow ~~~ -\frac{14}{5c_0} </math> |
<math>~=</math> |
<math>~ \frac{g^2}{a} </math> |
|
|
<math>~=</math> |
<math>~ g^2-\frac{7}{5} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{2}{5} + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 </math> |
|
<math>~\Rightarrow ~~~ 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 - 2\biggl(\frac{\rho_e}{\rho_c}\biggr) + \frac{2}{5}\biggl( 1-\frac{7}{c_0}\biggr) </math> |
<math>~=</math> |
<math>~ 0 \, .</math> |
The solution to this quadratic equation gives,
|
<math>~ \biggl(\frac{\rho_e}{\rho_c}\biggr) </math> |
<math>~=</math> |
<math>~ \frac{1}{6} \biggl[ 2 \pm \sqrt{4-\frac{24}{5}\biggl( 1-\frac{7}{c_0}\biggr)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{3} \biggl[ 1 \pm \sqrt{1-\frac{6}{5}\biggl( 1-\frac{7}{c_0}\biggr)} \biggr] </math> |
In order for this condition to hold while also meeting the demands of the eigenfrequency, we need <math>~\alpha</math> to satisfy the relation,
|
<math>~\frac{2}{3}\cdot \frac{7 + \alpha}{ (\alpha-1) \pm \sqrt{\alpha+1} }</math> |
<math>~=</math> |
<math>~ \frac{1}{3} \biggl[ 1 \pm \sqrt{1-\frac{6}{5}\biggl( 1-\frac{7}{c_0}\biggr)} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{14 + 2\alpha}{\alpha + c_0 }</math> |
<math>~=</math> |
<math>~ 1 \pm \biggl[ \frac{5c_0}{5c_0}-\frac{6}{5}\biggl( \frac{c_0-7}{c_0}\biggr) \biggr]^{1 / 2} </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{14 + \alpha -c_0}{\alpha + c_0 } \biggr]^2</math> |
<math>~=</math> |
<math>~ \frac{42-c_0}{5c_0} </math> |
|
<math>~\Rightarrow ~~~ 5c_0 (14 + \alpha -c_0)^2</math> |
<math>~=</math> |
<math>~ (42-c_0)(\alpha + c_0)^2 \, , </math> |
where, keep in mind,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
RESULT: After examining a range of physically reasonable values of <math>~\alpha</math>, we do not find any values for which the left-hand-side of this condition matches the right-hand-side.
Try Quartic Core Eigenfunction
Let's begin with Sterne's quartic function and see if we can match it to the envelope's power-law eigenfunction. From Sterne's presentation, we have,
|
<math>~x_\mathrm{core}</math> |
<math>~=</math> |
<math>~a\biggl[ 1-\frac{18}{5}\biggl( \frac{\xi}{g}\biggr)^2 +\frac{99}{35} \biggl( \frac{\xi}{g}\biggr)^4 \biggr]</math> |
and the associated eigenfrequency is obtained by setting,
<math>~\mathfrak{F} = \sigma^2 - 2\alpha = 36 \, .</math>
In this case, then, the eigenfrequency for the envelope will match the eigenfrequency of the core if,
|
<math>~36 + 2\alpha</math> |
<math>~=</math> |
<math>~ 3\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ (\alpha-1) \pm \sqrt{\alpha+1} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\rho_e}{\rho_c} \biggr) </math> |
<math>~=</math> |
<math>~ \frac{36 + 2\alpha}{ 3[(\alpha-1) \pm \sqrt{\alpha+1}] }</math> |
The eigenfunction for the envelope is, as before. The value of this envelope function will match the value of its core counterpart at the interface <math>~(\xi=1)</math> if,
|
<math>~a\biggl[ 1-\frac{18}{5}\biggl( \frac{1}{g}\biggr)^2 +\frac{99}{35} \biggl( \frac{1}{g}\biggr)^4 \biggr]</math> |
<math>~=</math> |
<math>~1</math> |
|
<math>~\Rightarrow ~~~ a</math> |
<math>~=</math> |
<math>~\biggl[ 1-\frac{18}{5}\biggl( \frac{1}{g}\biggr)^2 +\frac{99}{35} \biggl( \frac{1}{g}\biggr)^4 \biggr]^{-1} \, .</math> |
Finally, the slope (first derivative) of the core eigenfunction will match the slope of the envelope eigenfunction at the interface if,
|
<math>~\biggl( \frac{c_0}{a}\biggr) \xi^{c_0-1}\biggr|_\mathrm{\xi=1}</math> |
<math>~=</math> |
<math>~\biggl[ -\frac{36}{5g^2} \cdot \xi + \frac{4\cdot 99}{35g^4} \cdot \xi^3 \biggr]_\mathrm{\xi=1} </math> |
|
<math>~\Rightarrow ~~~c_0 \biggl[ 1-\frac{18}{5}\biggl( \frac{1}{g}\biggr)^2 +\frac{99}{35} \biggl( \frac{1}{g}\biggr)^4 \biggr]</math> |
<math>~=</math> |
<math>~ -\frac{36}{5g^2} + \frac{4\cdot 99}{35g^4} </math> |
|
<math>~\Rightarrow ~~~c_0 \biggl[ 35g^4-7\cdot 18g^2 +99 \biggr]</math> |
<math>~=</math> |
<math>~ - 7\cdot 36 g^2 + 4\cdot 99 \, . </math> |
Eureka Regarding Prasad's 1948 Paper
Envelope Solution Outline
C. Prasad (1948, MNRAS, 108, 414-416) has examined a closely related problem and, as it turns out, the mathematical approach that he used to solve that problem analytically is gratifyingly useful to me here. If, as above, we restrict our investigation to configurations for which,
<math>~g^2 = \mathcal{B} \, ,</math>
and if we multiply through by <math>~x/(\mathcal{A}\xi^2)</math>, our governing wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[1 - \frac{1}{\mathcal{A}} \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \frac{d^2x}{d\xi^2} + \biggl[ 3 - \frac{6}{\mathcal{A}}\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \frac{1}{\mathcal{A}}\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \biggr]\frac{x}{\xi^2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[1 - \mathcal{D} \xi^3\biggr] \frac{d^2x}{d\xi^2} + \biggl[ 3 - 6\mathcal{D} \xi^3 \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \biggr]\frac{x}{\xi^2} \, , </math> |
where,
<math>\mathcal{D} \equiv \frac{1}{\mathcal{A}} \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 = \biggl(\frac{\rho_e}{\rho_c}\biggr)^2\biggl[2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr)\biggr]^{-1} = \biggl[2 \biggl(\frac{\rho_c}{\rho_e}-1 \biggr)\biggr]^{-1} \, .</math>
This wave equation is very similar to equation (2) of Prasad (1948). If, following Prasad's guidance, we then assume a series solution of the form,
|
<math>~x</math> |
<math>~=</math> |
<math>~ \xi^{c_0} \sum_0^\infty a_k \xi^k \, , </math> |
the indicial equation gives,
<math>~c_0 = -1 \pm \sqrt{1+\alpha} \, .</math>
This is precisely the value of the exponent, <math>~c_0</math>, that we derived — in a more stumbling fashion — above and, as is shown by the following framed image, it is identical to the exponent derived by Prasad (1948).
|
Equation and accompanying text extracted† from C. Prasad (1948)
"Radial Oscillations of a Particular Stellar Model"
Monthly Notices of the Royal Astronomical Society, vol. 108, pp. 414-416 © Royal Astronomical Society |
|---|
| †Displayed here exactly as presented in the original publication. |
Using equation (7) from Prasad (1948) as a guide, we hypothesize that the eigenfrequency of the jth mode in the envelope is given by the relation,
|
<math>~ \sigma_j^2 \biggr|_\mathrm{env} </math> |
<math>~=</math> |
<math>~(c_0 + 3j)(c_0 + 3j+5) + 2\alpha_e </math> |
|
|
<math>~=</math> |
<math>~3[\alpha_e + c_0(2j+1) + j(3j+5)] \, ,</math> |
where, the last expression results from recognizing that <math>~\alpha_e = c_0^2 + 2c_0 \, ,</math> and we have adopted the notation,
<math>~ \sigma_j^2\biggr|_\mathrm{env} \equiv \biggl(\mathfrak{F} + 2\alpha\biggr)\frac{\rho_c}{\rho_e} = \frac{3\omega^2}{2\pi \gamma_\mathrm{g} G\rho_e} \, . </math>
And guided by equation (6) from Prasad (1948), we hypothesize that successive coefficients in the (truncated) series that defines the radial structure of each mode is governed by the recurrence relation,
|
<math>~\frac{1}{\mathcal{D}}\cdot \frac{a_{k+3}}{a_k}</math> |
<math>~=</math> |
<math>~ \frac{(c_0+k)(c_0+k+5) - (\sigma_j^2 - 2\alpha)}{(c_0 + k + 3)(c_0+k+5) - \alpha} \, . </math> |
Example Envelope Eigenvectors
Mode j = 0
Here we assume that the series defining the eigenfunction has only one term. This should match our earlier restricted solution. Specifically,
|
<math>~x_{j=0}</math> |
<math>~=</math> |
<math>~a_0 \xi^{c_0}</math> |
|
<math>~\Rightarrow ~~~\frac{1}{\xi} \cdot \frac{d x_{j=0}}{d\xi}</math> |
<math>~=</math> |
<math>~a_0 c_0 \xi^{c_0-2} \, ;</math> |
|
<math>~\Rightarrow ~~~\frac{d^2 x_{j=0}}{d\xi^2}</math> |
<math>~=</math> |
<math>~a_0 c_0(c_0-1) \xi^{c_0-2} \, .</math> |
In this case, the wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~a_0 \xi^{c_0-2}\biggl\{ \biggl[1 - \mathcal{D} \xi^3\biggr] c_0(c_0-1) + \biggl[ 3 - 6\mathcal{D} \xi^3 \biggr] c_0 + \biggl[ \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \biggr] \biggr\} \, . </math> |
The coefficients of the <math>~\xi^0</math> terms will sum to zero if the above-defined indicial exponent condition is satisfied; that is, by setting,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
In order for the coefficients of the <math>~\xi^3</math> terms to sum to zero, we need,
|
<math>~\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha \biggr) - 2\alpha</math> |
<math>~=</math> |
<math>~c_0(c_0-1) +6c_0 </math> |
|
<math>~\Rightarrow ~~~ \sigma^2_{j=0}\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~c_0(c_0+5) + 2\alpha \, .</math> |
Mode j = 1
Here we assume that the series defining the eigenfunction has two terms: <math>~k=0</math> and <math>~k=3</math>. Specifically,
|
<math>~x_{j=1}</math> |
<math>~=</math> |
<math>~a_0 \xi^{c_0} + a_3 \xi^{c_0+3}</math> |
|
<math>~\Rightarrow ~~~\frac{1}{\xi}\cdot \frac{d x_{j=1}}{d\xi}</math> |
<math>~=</math> |
<math>~a_0 c_0 \xi^{c_0-2} + a_3 (c_0+3) \xi^{c_0+1} \, ;</math> |
|
<math>~\Rightarrow ~~~\frac{d^2 x_{j=1}}{d\xi^2}</math> |
<math>~=</math> |
<math>~a_0 c_0(c_0-1) \xi^{c_0-2} + a_3 (c_0+3)(c_0+2) \xi^{c_0+1} \, .</math> |
In this case, after factoring out <math>~a_0\xi^{c_0-2}</math>, the wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[1 - \mathcal{D} \xi^3\biggr] \biggl[ c_0(c_0-1) + \frac{a_3}{a_0} (c_0+3)(c_0+2) \xi^{3} \biggr] + \biggl[ 3 - 6\mathcal{D} \xi^3 \biggr] \biggl[c_0 + \frac{a_3}{a_0} (c_0+3) \xi^{3}\biggr] </math> |
|
|
|
<math>~ + \biggl[ \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \biggr] \biggl[1 + \frac{a_3}{a_0} \xi^{3} \biggr] \, . </math> |
Again, the coefficients of the <math>~\xi^0</math> terms will sum to zero if the above-defined indicial exponent condition is satisfied; that is, by setting,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
In order for the coefficients of the <math>~\xi^3</math> terms to sum to zero, we need,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -\mathcal{D} c_0(c_0-1)+ \frac{a_3}{a_0} (c_0+3)(c_0+2) -6\mathcal{D}c_0 + \frac{3a_3}{a_0} (c_0+3) + \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)-\frac{\alpha a_3}{a_0} </math> |
|
<math>~\Rightarrow~~~ \frac{a_3}{a_0} \biggl[ (c_0+3)(c_0+2) + 3(c_0+3)-\alpha\biggr] </math> |
<math>~=</math> |
<math>~ \mathcal{D}\biggl[ c_0(c_0-1) +6c_0 -\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha \biggr) + 2\alpha \biggr] </math> |
|
<math>~\Rightarrow~~~ \frac{1}{\mathcal{D}} \cdot \frac{a_3}{a_0} \biggl[ (c_0+3)(c_0+5) -\alpha\biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ c_0(c_0+5) -\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha \biggr) + 2\alpha \biggr] </math> |
|
<math>~\Rightarrow~~~ \frac{1}{\mathcal{D}} \cdot \frac{a_3}{a_0} </math> |
<math>~=</math> |
<math>~\frac{ c_0(c_0+5) - (\sigma^2_{j=1} - 2\alpha) }{ (c_0+3)(c_0+5) -\alpha} \, . </math> |
In addition, we must also examine what condition is required for the <math>~\xi^6</math> terms to sum to zero. We have,
|
<math>~0</math> |
<math>~=</math> |
<math>~\mathcal{D}\frac{a_3}{a_0}\biggl[ - (c_0+3)(c_0+2) -6(c_0+3) + \biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr) \biggr] </math> |
|
<math>~\Rightarrow ~~~ \sigma^2_{j=1}\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ (c_0+3)(c_0+8) +2\alpha \, . </math> |
Mode j = 2
Here we assume that the series defining the eigenfunction has three terms: <math>~k=0</math>, <math>~k=3</math>, and <math>~k=6</math>. Specifically,
|
<math>~x_{j=2}</math> |
<math>~=</math> |
<math>~a_0 \xi^{c_0} + a_3 \xi^{c_0+3} + a_6 \xi^{c_0+6}</math> |
|
<math>~\Rightarrow ~~~\frac{1}{\xi}\cdot \frac{d x_{j=2}}{d\xi}</math> |
<math>~=</math> |
<math>~\frac{1}{\xi} \biggl[ a_0 c_0 \xi^{c_0-1} + a_3 (c_0+3) \xi^{c_0+2} + a_6(c_0+6)\xi^{c_0+5} \biggr] \, ;</math> |
|
<math>~\Rightarrow ~~~\frac{d^2 x_{j=2}}{d\xi^2}</math> |
<math>~=</math> |
<math>~a_0 c_0(c_0-1) \xi^{c_0-2} + a_3 (c_0+3)(c_0+2) \xi^{c_0+1} + a_6(c_0+6)(c_0+5) \xi^{c_0+4} \, .</math> |
In this case, after factoring out <math>~a_0\xi^{c_0-2}</math>, the wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[1 - \mathcal{D} \xi^3\biggr] \biggl[ c_0(c_0-1) + \frac{a_3}{a_0} (c_0+3)(c_0+2) \xi^{3} + \frac{a_6}{a_0}(c_0+6)(c_0+5) \xi^{6} \biggr] </math> |
|
|
|
<math>~ + \biggl[ 3 - 6\mathcal{D} \xi^3 \biggr] \biggl[ c_0 + \frac{a_3}{a_0} (c_0+3) \xi^{3} + \frac{a_6}{a_0}(c_0+6)\xi^{6} \biggr] + \biggl[ \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \biggr] \biggl[1 + \frac{a_3}{a_0} \xi^{3} + \frac{a_6}{a_0} \xi^{6} \biggr] \, . </math> |
Again, the coefficients of the <math>~\xi^0</math> terms will sum to zero if,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
In order for the coefficients of the <math>~\xi^3</math> terms to sum to zero, we need,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -\mathcal{D}c_0(c_0-1) + \frac{a_3}{a_0} (c_0+3)(c_0+2) - 6\mathcal{D}c_0 + 3\cdot \frac{a_3}{a_0} (c_0+3) + \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr) - \alpha\cdot \frac{a_3}{a_0} </math> |
|
<math>~\Rightarrow~~~ \frac{1}{\mathcal{D}} \cdot \frac{a_3}{a_0} \biggl[ (c_0+3)(c_0+2) + 3 (c_0+3) - \alpha\biggr] </math> |
<math>~=</math> |
<math>~ c_0(c_0-1) + 6c_0 +2\alpha - \biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha \biggr) </math> |
|
<math>~\Rightarrow~~~ \frac{1}{\mathcal{D}} \cdot \frac{a_3}{a_0} </math> |
<math>~=</math> |
<math>~ \frac{ c_0(c_0+5) +2\alpha - \sigma^2_{j=2} }{ (c_0+3)(c_0+5) - \alpha } </math> |
In order for the coefficients of the <math>~\xi^6</math> terms to sum to zero, we need,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{a_6}{a_0}(c_0+6)(c_0+5) - \mathcal{D} \cdot \frac{a_3}{a_0} (c_0+3)(c_0+2) +3 \cdot \frac{a_6}{a_0}(c_0+6) - 6\mathcal{D}\cdot \frac{a_3}{a_0} (c_0+3) -\alpha \cdot \frac{a_6}{a_0} + \mathcal{D}\biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr) \cdot \frac{a_3}{a_0} </math> |
|
<math>~\Rightarrow ~~~ \frac{a_6}{a_0} \biggl[ (c_0+6)(c_0+5) +3 (c_0+6) -\alpha \biggr] </math> |
<math>~=</math> |
<math>~ \mathcal{D} \cdot \frac{a_3}{a_0} \biggl[ (c_0+3)(c_0+2) +6 (c_0+3) +2\alpha - \sigma^2_{j=2} \biggr] </math> |
|
<math>~\Rightarrow ~~~\frac{1}{\mathcal{D}} \cdot \frac{a_6}{a_3} </math> |
<math>~=</math> |
<math>~ \frac{ (c_0+3)(c_0+8) - (\sigma^2_{j=2}-2\alpha) }{(c_0+6)(c_0+8) -\alpha } \, . </math> |
And the frequency determined from setting to zero the sum of coefficients of the <math>~\xi^9</math> terms is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -\mathcal{D} \cdot \frac{a_6}{a_0}(c_0+6)(c_0+5) - 6\mathcal{D} \cdot \frac{a_6}{a_0}(c_0+6) + \mathcal{D} \biggl(\frac{\rho_c}{\rho_e}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\cdot \frac{a_6}{a_0} </math> |
|
|
<math>~=</math> |
<math>~ -\mathcal{D} \cdot \frac{a_6}{a_0} \biggl[ (c_0+6)(c_0+5) + 6(c_0+6) - (\sigma^2_{j=2} - 2\alpha) \biggr] </math> |
|
<math>~\Rightarrow ~~~ (\sigma^2_{j=2} - 2\alpha) </math> |
<math>~=</math> |
<math>~ (c_0+6)(c_0+11) \, . </math> |
Match Prasad-like Envelope Eigenvector to the Core Eigenvector
If we define,
<math>~\eta \equiv \frac{\xi}{g} \, ,</math>
the above wave equation for the core becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1 - \eta^2)\frac{d^2x}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} + \mathfrak{F} x \, . </math> |
Not surprisingly, this is identical in form to the eigenvalue problem first presented by Sterne (1937) in connection with an examination of radial oscillations in uniform-density spheres. For the core of our zero-zero bipolytrope, we can therefore adopt any one of the polynomial eigenfunctions and corresponding eigenfrequencies derived by Sterne. We will insist that the eigenfrequency of the envelope match the eigenfrequency of the core; and, following J. O. Murphy & R. Fiedler (1985b) (see the top paragraph of the right-hand column on p. 223 of their article), we seek solutions for which there is continuity in both the eigenfunction and its first derivative at the interface <math>~(\xi = 1)</math>.
Eigenfrequencies
We must note that, heretofore, we have used the following dimensionless frequency notations:
|
<math>~\sigma^2|_\mathrm{core} \equiv \frac{3\omega^2_\mathrm{core}}{2\pi \gamma_g G\rho_c} \, ,</math> |
and |
<math>~\sigma^2|_\mathrm{env} \equiv \frac{3\omega^2_\mathrm{env}}{2\pi \gamma_g G\rho_e} \, .</math> |
This means that, demanding that the two dimensional frequencies <math>~(\omega)</math> be the same requires that the ratio of the dimensionless frequencies <math>~(\sigma)</math> be,
|
<math>~\frac{ \sigma^2|_\mathrm{core}}{\sigma^2|_\mathrm{env} }</math> |
<math>~=</math> |
<math>~\frac{\rho_e}{\rho_c} \, .</math> |
Now, according to Sterne's derivation, the dimensionless eigenfrequency associated with the <math>~j^\mathrm{th}</math> mode in the core is,
|
<math>~\sigma^2_j|_\mathrm{core}</math> |
<math>~=</math> |
<math>~2\alpha + \mathfrak{F}_j = 2\alpha + 2j(2j+5) \, .</math> |
And, as we have just discussed, the dimensionless eigenfrequency associated with the <math>~\ell^\mathrm{th}</math> Prasad-like mode in the envelope is,
|
<math>~\sigma^2_\ell|_\mathrm{env}</math> |
<math>~=</math> |
<math>~2\alpha + \mathfrak{F}_\ell = 2\alpha + (c_0 + 3\ell)(c_0 + 3\ell +5) \, ,</math> |
where,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~-1 \pm (1+\alpha)^{1 / 2} \, .</math> |
Hence, in order for any specific pair of modes to have the same dimensional eigenfrequencies, we must have an envelope-to-core density ratio given by the expression,
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~ \frac{ 2\alpha + 2j(2j+5) }{ 2\alpha + (c_0 + 3\ell)(c_0 + 3\ell +5) } \, . </math> |
Put another way, the ratio of the dimensional eigenfrequencies is,
|
<math>~ \frac{\omega^2_\mathrm{env}}{\omega^2_\mathrm{core}} </math> |
<math>~=</math> |
<math>~\frac{\sigma^2_\mathrm{env}}{\sigma^2_\mathrm{core}} \biggl( \frac{\rho_e}{\rho_c} \biggr) = \frac{ 2\alpha + (c_0 + 3\ell)(c_0 + 3\ell +5) }{ 2\alpha + 2j(2j+5) } \biggl( \frac{\rho_e}{\rho_c} \biggr)\, . </math> |
We also should keep in mind that, in our particular case, the envelope density must not be greater than the core density. So, demanding that the (dimensional) eigenfrequencies be equal and, simultaneously, that <math>~\rho_e/\rho_c \le 1</math>, implies the following constraint on the integer index, <math>~j</math> for each choice of the index, <math>~\ell</math>:
|
<math>~2\alpha + 2j(2j+5)</math> |
<math>~\le</math> |
<math>~2\alpha + (c_0 + 3\ell)(c_0 + 3\ell +5) </math> |
|
<math>\Rightarrow~~~2j</math> |
<math>~\le</math> |
<math>~ c_0 + 3\ell </math> |
|
<math>\Rightarrow~~~j</math> |
<math>~\le j_\mathrm{max} \equiv</math> |
<math>~\mathrm{INT}\biggl[ \frac{1}{2}(c_0 + 3\ell ) \biggr] \, .</math> |
The following table lists values of <math>~j_\mathrm{max}</math> for various values of the companion index, <math>~\ell</math>, and an assumed value of the parameter,
<math>~\alpha \equiv 3 - 4/\gamma_g = \frac{3-n}{n+1} \, .</math>
| Limiting Index, <math>~j_\mathrm{max}</math>, assuming <math>c_0 = \sqrt{1+\alpha} -1</math> |
|||
| <math>~\ell</math> | <math>~(n,\gamma_\mathrm{g}, \alpha,c_0)</math> | ||
| <math>~(0,\infty,3,1)</math> | <math>~(3,\tfrac{4}{3},0,0)</math> | <math>~(\infty,1, -1,-1)</math> | |
| 0 | 0 | 0 | --- |
| 1 | 2 | 1 | 1 |
| 2 | 3 | 3 | 2 |
| 3 | 5 | 4 | 4 |
| 4 | 6 | 6 | 5 |
| 5 | 8 | 7 | 7 |
| 6 | 9 | 9 | 8 |
| 7 | 11 | 10 | 10 |
| 8 | 12 | 12 | 11 |
| 9 | 14 | 13 | 13 |
| 10 | 15 | 15 | 14 |
| Limiting Index, <math>~j_\mathrm{max}</math>, assuming <math>c_0 = -\sqrt{1+\alpha} -1</math> |
|||
| <math>~\ell</math> | <math>~(n,\gamma_\mathrm{g}, \alpha,c_0)</math> | ||
| <math>~(\infty,1, -1,-1)</math> | <math>~(3,\tfrac{4}{3},0,-2)</math> | <math>~(0,\infty,3,-3)</math> | |
| 0 | --- | --- | --- |
| 1 | 1 | 0 | 0 |
| 2 | 2 | 2 | 1 |
| 3 | 4 | 3 | 3 |
| 4 | 5 | 5 | 4 |
| 5 | 7 | 6 | 6 |
| 6 | 8 | 8 | 7 |
| 7 | 10 | 9 | 9 |
| 8 | 11 | 11 | 10 |
| 9 | 13 | 12 | 12 |
| 10 | 14 | 14 | 13 |
Implications
Keeping in mind that,
|
<math>~g^2</math> |
<math>~\equiv</math> |
<math>~ 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, , </math> |
and that, in order for the Prasad-like modes to be relevant in the envelope, we must have,
|
<math>~g^2 = \mathcal{B}</math> |
<math>~\equiv</math> |
<math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2</math> |
|
|
<math>~=</math> |
<math>~\biggl(1 - \frac{\rho_e}{\rho_c}\biggr)\biggl[ 3\biggl(\frac{\rho_e}{\rho_c}\biggr)+1\biggr] \, .</math> |
we recognize that once the eigenfrequency match is used to define the relevant value of the density ratio, <math>~\rho_e/\rho_c</math>, the relevant values of both <math>~q</math> and <math>~\nu</math> are set as well. Specifically, as derived above, in the context of our "more general" envelope solution,
|
<math>~q^3 = \frac{(\rho_e/\rho_c)}{2[1-(\rho_e/\rho_c)]}</math> |
and |
<math>~\nu = \frac{1}{3[1-(\rho_e/\rho_c)]} \, .</math> |
This also means that the parameter,
|
<math>~\mathcal{D}</math> |
<math>~=</math> |
<math>~\biggl[2\biggr(\frac{\rho_c}{\rho_e} - 1\biggr)\biggr]^{-1} = q^3 \, .</math> |
Eigenfunctions
The eigenfunction associated with the <math>~j^\mathrm{th}</math> Sterne-like mode of the core is,
|
<math>~x_j|_\mathrm{core}</math> |
<math>~=</math> |
<math>~\sum_{i=0}^{j} a_{2i} \biggl( \frac{\xi^2}{g^2}\biggr)^{i} \, ,</math> |
where, for the specified, <math>~j^\mathrm{th}</math> mode, the value of the leading coefficient, <math>~a_0</math>, is arbitrary, but for all other coefficients,
|
<math>~\frac{a_{k+2}}{a_k }</math> |
<math>~=</math> |
<math>~ \frac{k^2 + 5k - \mathfrak{F}_j}{(k+2)(k+5)} \, .</math> |
|
|
<math>~=</math> |
<math>~ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \, .</math> |
The eigenfunction associated with the <math>~\ell^\mathrm{th}</math> Prasad-like mode of the envelope is,
|
<math>~x_\ell|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \xi^{c_0} \sum_{i=0}^\ell b_{3i} \xi^{3i} \, , </math> |
where, for the specified, <math>~\ell^\mathrm{th}</math> mode, the value of the leading coefficient, <math>~a_0</math>, is arbitrary, but for all other coefficients,
|
<math>~\frac{1}{q^3}\cdot \frac{b_{k+3}}{b_k}</math> |
<math>~=</math> |
<math>~ \frac{(c_0+k)(c_0+k+5) - \mathfrak{F}_\ell}{(c_0 + k + 3)(c_0+k+5) - \alpha} </math> |
|
|
<math>~=</math> |
<math>~ \frac{(c_0+k)(c_0+k+5) - (c_0 + 3\ell)(c_0 + 3\ell +5)}{(c_0 + k + 3)(c_0+k+5) - \alpha} \, . </math> |
Example11
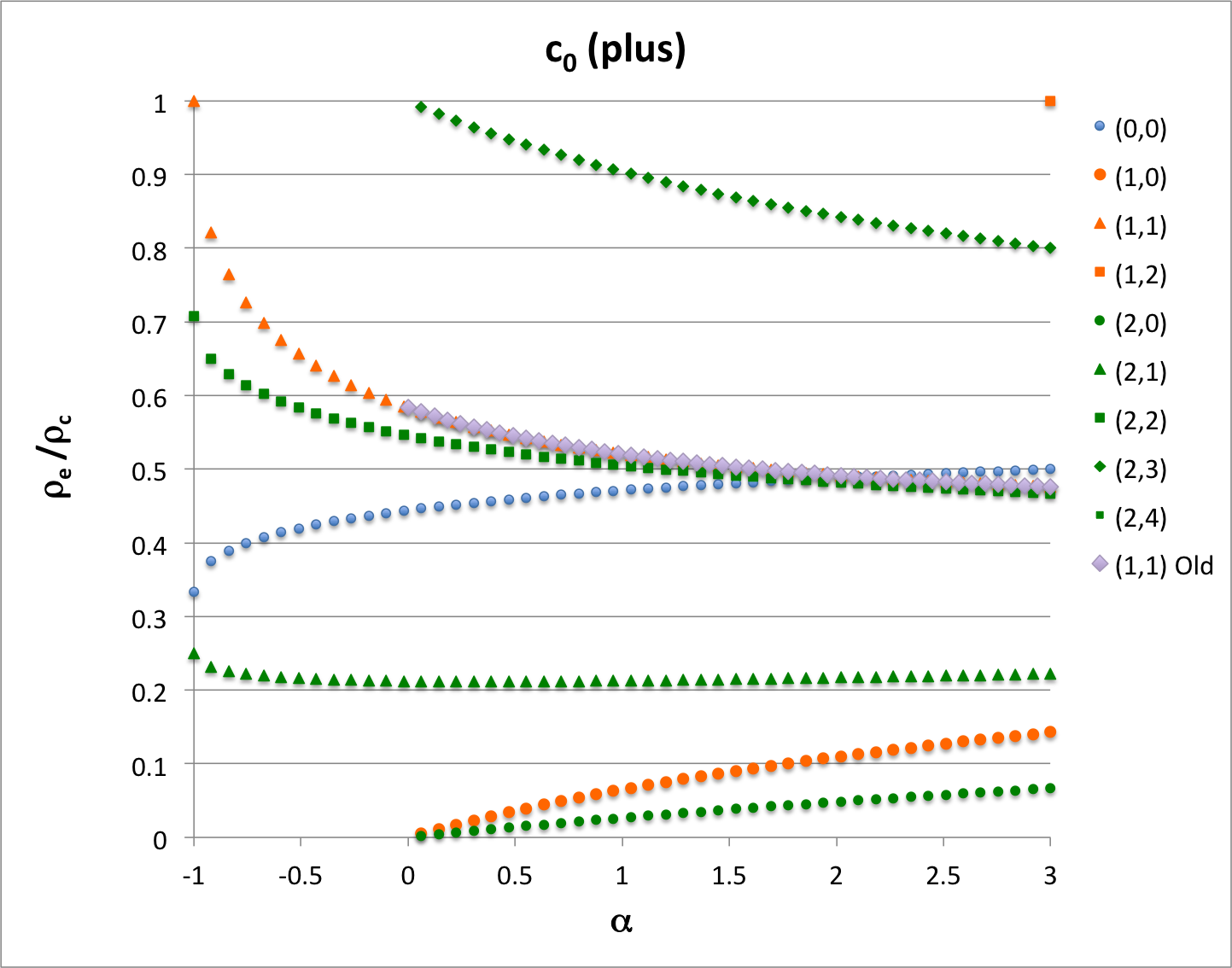
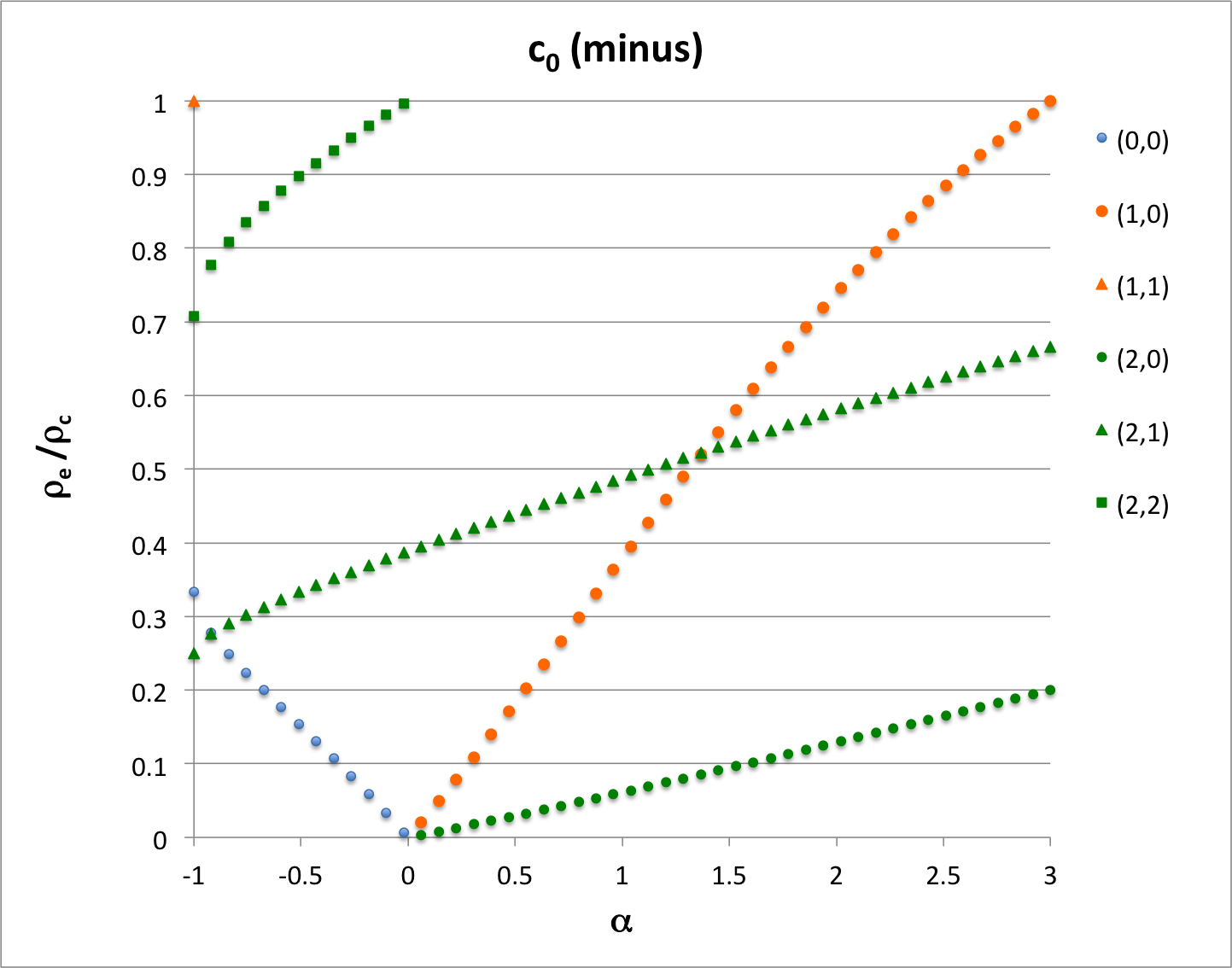
Let's try <math>~(\ell,j) = (1,1) \, .</math>
|
<math>~x_1 |_\mathrm{core}</math> |
<math>~=</math> |
<math>~a_0\biggl[1 + \frac{a_2}{a_0} \biggl(\frac{\xi}{g}\biggr)^2 \biggr]</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl\{1 + \biggl[ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \biggr]_{k=0} \biggl(\frac{\xi}{g}\biggr)^2 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl[1 - \frac{7}{5} \biggl(\frac{\xi}{g}\biggr)^2 \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{dx_1}{d\xi}\biggr|_\mathrm{core}</math> |
<math>~=</math> |
<math>~- a_0 \cdot \frac{14}{5} \biggl(\frac{\xi}{g^2}\biggr) </math> |
|
<math>~x_1|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl[1 + \frac{b_{3}}{b_0} \xi^{3} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl\{ 1 + \biggl[ \frac{(c_0+k)(c_0+k+5) - (c_0 + 3\ell)(c_0 + 3\ell +5)}{(c_0 + k + 3)(c_0+k+5) - \alpha}\biggr]_{k=0} \xi^{3} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl\{ 1 + \biggl[ \frac{c_0(c_0+5) - (c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha}\biggr] \xi^{3} \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{dx_1}{d\xi}\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ b_0 \xi^{c_0-1}\biggl\{ c_0 + c_0\biggl[ \frac{c_0(c_0+5) - (c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha}\biggr] \xi^{3} +\biggl[ \frac{3c_0(c_0+5) - 3(c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha}\biggr] \xi^{3} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0-1}\biggl\{ c_0 + \biggl[ \frac{c_0^2(c_0+5) - c_0(c_0 + 3)(c_0 + 8)+ 3c_0(c_0+5) - 3(c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \xi^{3} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0-1}\biggl\{ c_0 + (c_0+3)\biggl[ \frac{c_0(c_0+5) - (c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \xi^{3} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0-1}\biggl\{ c_0 - \biggl[ \frac{6(c_0+3)(c_0+4)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \xi^{3} \biggr\} </math> |
Let's define both <math>~a_0</math> and <math>~b_0</math> such that the values of both eigenfunctions is unity at the interface <math>~(\xi=1)</math>. This means that,
|
<math>~a_0</math> |
<math>~=</math> |
<math>~\biggl[1 - \frac{7}{5g^2} \biggr]^{-1} =\biggl[\frac{5g^2}{5g^2-7} \biggr] \, ;</math> |
|
<math>~b_0</math> |
<math>~=</math> |
<math>~\biggl\{ 1 + \biggl[ \frac{c_0(c_0+5) - (c_0 + 3)(c_0 + 8)}{(c_0 + 3)(c_0+8) - \alpha}\biggr] \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(c_0 + 3)(c_0+8) - \alpha}{c_0(c_0+5)- \alpha }\biggr] \, .</math> |
Hence, in order for the first derivative of both eigenfunctions to be equal at the interface, we need,
|
<math>~- a_0 \cdot \frac{14}{5} \biggl(\frac{1}{g^2}\biggr) </math> |
<math>~=</math> |
<math>~ b_0 \biggl\{ c_0 - \biggl[ \frac{6(c_0+3)(c_0+4)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ - \biggl[\frac{5g^2}{5g^2-7} \biggr] \cdot \frac{14}{5g^2} </math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{c_0[(c_0 + 3)(c_0+8) - \alpha ]-6(c_0+3)(c_0+4)}{(c_0 + 3)(c_0+8) - \alpha} \biggr\}\biggl[ \frac{(c_0 + 3)(c_0+8) - \alpha}{c_0(c_0+5)- \alpha }\biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{14}{7-5g^2} </math> |
<math>~=</math> |
<math>~ \frac{c_0[(c_0 + 3)(c_0+8) - \alpha ]-6(c_0+3)(c_0+4)}{c_0(c_0+5)- \alpha } </math> |
|
<math>~\Rightarrow ~~~ \frac{7-5g^2}{14} </math> |
<math>~=</math> |
<math>~ \frac{c_0(c_0+5)- \alpha }{c_0[(c_0 + 3)(c_0+8) - \alpha ]-6(c_0+3)(c_0+4)} </math> |
|
<math>~\Rightarrow ~~~ g^2 </math> |
<math>~=</math> |
<math>~\frac{7}{5}+ \frac{14}{5} \biggl[ \frac{\alpha -c_0(c_0+5)}{c_0[(c_0 + 3)(c_0+8) - \alpha ]-6(c_0+3)(c_0+4)}\biggr] \, . </math> |
Example12
Let's try <math>~(\ell,j) = (1,2) \, .</math>
|
<math>~x_1 |_\mathrm{core}</math> |
<math>~=</math> |
<math>~a_0 + a_2\biggl(\frac{\xi}{g}\biggr)^2 + a_4\biggl(\frac{\xi}{g}\biggr)^4</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl[ 1 + \frac{a_2}{a_0}\biggl(\frac{\xi}{g}\biggr)^2 + \frac{a_4}{a_2} \cdot \frac{a_2}{a_0} \biggl(\frac{\xi}{g}\biggr)^4 \biggr]</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl\{1 + \biggl[ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \biggr]_{k=0} \biggl(\frac{\xi}{g}\biggr)^2 + \biggl[ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \biggr]_{k=2} \biggl[ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \biggr]_{k=0} \biggl(\frac{\xi}{g}\biggr)^4 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl[ 1 - \frac{18}{5} \biggl(\frac{\xi}{g}\biggr)^2 + \frac{99}{35} \biggl(\frac{\xi}{g}\biggr)^4 \biggr] \, ;</math> |
|
<math>~\Rightarrow ~~~ \frac{dx_1}{d\xi}\biggr|_\mathrm{core}</math> |
<math>~=</math> |
<math>~a_0 \biggl[ - \frac{36}{5} \biggl(\frac{\xi}{g^2} \biggr) + \frac{4\cdot 99}{35} \biggl(\frac{\xi^3}{g^4}\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{a_0}{35g^4} \biggl[ - 7\cdot 36 g^2 \xi + 4\cdot 99 \xi^3 \biggr] \, .</math> |
In order for the core's <math>~x_2</math> eigenfunction to have the value of unity at <math>~\xi=1</math>, we need,
|
<math>~1</math> |
<math>~=</math> |
<math>~a_0\biggl[ 1 - \frac{18}{5} \biggl(\frac{1}{g}\biggr)^2 + \frac{99}{35} \biggl(\frac{1}{g}\biggr)^4 \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{a_0}{35g^4} \biggl[ 35 g^4 - 7\cdot 18g^2 + 99 \biggr] </math> |
|
<math>~\Rightarrow ~~~ a_0 </math> |
<math>~=</math> |
<math>~35g^4 \biggl[ 35 g^4 - 7\cdot 18g^2 + 99 \biggr]^{-1} </math> |
Hence, in order for the first derivative of both eigenfunctions to be equal at the interface, we need,
|
<math>~ \frac{ a_0}{35g^4}\biggl[ - 7\cdot 36 g^2 + 4\cdot 99 \biggr] </math> |
<math>~=</math> |
<math>~ b_0 \biggl\{ c_0 - \biggl[ \frac{6(c_0+3)(c_0+4)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow~~~35g^4 \biggl[ 35 g^4 - 7\cdot 18g^2 + 99 \biggr]^{-1} \frac{ 1}{35g^4}\biggl[ - 7\cdot 36 g^2 + 4\cdot 99 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(c_0 + 3)(c_0+8) - \alpha}{c_0(c_0+5)- \alpha }\biggr] \biggl\{ c_0 - \biggl[ \frac{6(c_0+3)(c_0+4)}{(c_0 + 3)(c_0+8) - \alpha} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow~~~ 36\biggl[ 35 g^4 - 7\cdot 18g^2 + 99 \biggr]^{-1} \biggl[ 11 - 7g^2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{c_0[ (c_0 + 3)(c_0+8) - \alpha] - 6(c_0+3)(c_0+4)}{c_0(c_0+5)- \alpha} \biggr] </math> |
|
<math>~\Rightarrow~~~ \biggl[ 11 - 7g^2 \biggr] </math> |
<math>~=</math> |
<math>~ \frac{1}{\mathcal{H} } \biggl[ 35 g^4 - 7\cdot 18g^2 + 99 \biggr] </math> |
|
<math>~\Rightarrow~~~ 0</math> |
<math>~=</math> |
<math>~ 35 g^4 - 7\cdot 18g^2 + 99 - \mathcal{H}\biggl( 11 - 7g^2 \biggr) </math> |
|
|
<math>~=</math> |
<math>~ 35 g^4 - 7( 18-\mathcal{H} )g^2 + 11 (9-\mathcal{H}) \, , </math> |
where,
|
<math>~\mathcal{H}</math> |
<math>~\equiv</math> |
<math>~36\biggl[ \frac{c_0(c_0+5)- \alpha}{c_0[ (c_0 + 3)(c_0+8) - \alpha] - 6(c_0+3)(c_0+4)} \biggr] \, . </math> |
The solution to this quadratic equation gives,
|
<math>~g^2</math> |
<math>~=</math> |
<math>~ \frac{1}{70} \biggl\{7( 18-\mathcal{H} ) \pm \sqrt{7^2 ( 18-\mathcal{H} )^2 - 44 \cdot 35(9-\mathcal{H}) } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{7( 18-\mathcal{H} )}{70} \biggl\{1 \pm \sqrt{1 - \frac{44 \cdot 35(9-\mathcal{H})}{7^2 ( 18-\mathcal{H} )^2} } \biggr\} \, . </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Example21
Let's try <math>~(\ell,j) = (2,1) \, .</math>
|
<math>~x_1 |_\mathrm{core}</math> |
<math>~=</math> |
<math>~a_0\biggl[1 + \frac{a_2}{a_0} \biggl(\frac{\xi}{g}\biggr)^2 \biggr]</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl\{1 + \biggl[ \frac{k^2 + 5k - 2j(2j+5)}{(k+2)(k+5)} \biggr]_{k=0} \biggl(\frac{\xi}{g}\biggr)^2 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~a_0\biggl[1 - \frac{7}{5} \biggl(\frac{\xi}{g}\biggr)^2 \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{dx_1}{d\xi}\biggr|_\mathrm{core}</math> |
<math>~=</math> |
<math>~- a_0 \cdot \frac{14}{5} \biggl(\frac{\xi}{g^2}\biggr) </math> |
|
<math>~x_2|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl[1 + \frac{b_{3}}{b_0} \xi^{3} + \frac{b_{3}}{b_0}\cdot \frac{b_{6}}{b_3} \xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl\{ 1 + \mathcal{D} \biggl[ \frac{(c_0+k)(c_0+k+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + k + 3)(c_0+k+5) - \alpha}\biggr]_{k=0} \xi^{3} </math> |
|
|
|
<math>~ + \mathcal{D}^2 \biggl[ \frac{(c_0+k)(c_0+k+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + k + 3)(c_0+k+5) - \alpha}\biggr]_{k=0} \biggl[ \frac{(c_0+k)(c_0+k+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + k + 3)(c_0+k+5) - \alpha}\biggr]_{k=3}\xi^{6} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ b_0 \xi^{c_0}\biggl\{ 1 + \mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \xi^{3} </math> |
|
|
|
<math>~ + \mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr]\xi^{6} \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{dx_2}{d\xi}\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ b_0 \xi^{c_0-1}\biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \xi^{3} </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr]\xi^{6} \biggr\} </math> |
Let's define both <math>~a_0</math> and <math>~b_0</math> such that the values of both eigenfunctions is unity at the interface <math>~(\xi=1)</math>. This means that,
|
<math>~a_0</math> |
<math>~=</math> |
<math>~\biggl[1 - \frac{7}{5g^2} \biggr]^{-1} =\biggl[\frac{5g^2}{5g^2-7} \biggr] \, ;</math> |
|
<math>~b_0</math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] + \mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\}^{-1} </math> |
Hence, in order for the first derivative of both eigenfunctions to be equal at the interface, we need,
|
<math>~- \frac{1}{b_0} \cdot \frac{14}{5} \biggl(\frac{1}{g^2}\biggr) </math> |
<math>~=</math> |
<math>~ \frac{1}{a_0} \biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
<math>~\Rightarrow~~~ 0 </math> |
<math>~=</math> |
<math>~ \biggl[1 - \frac{7}{5g^2} \biggr]\biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{14}{5} \biggl(\frac{1}{g^2}\biggr) \biggl\{ 1 + \mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + \mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} \, . </math> |
But, we can show that,
<math>\frac{1}{g} = (1+2\mathcal{D}) \, .</math>
|
WRONG! This relation should read,
|
Hence,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~ \biggl[1 - \frac{7}{5}\biggl(1+\mathcal{D}\biggr)^2 \biggr]\biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{7}{5} \biggl(1+\mathcal{D}\biggr)^2 \biggl\{ 2 + 2\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + 2\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{7}{5} \biggl(1+\mathcal{D}\biggr)^2 \biggl\{ (2 -c_0 ) + 2\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] - (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + 2\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] </math> |
|
|
|
<math>~ - (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{7}{5} \biggl(1+\mathcal{D}\biggr)^2 \biggl\{ (2 -c_0 ) - (c_0+1)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] </math> |
|
|
|
<math>~ - (c_0 +4)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha}\biggr] \biggr\} </math> |
Allow Different Adiabatic Exponents
Let's allow the core to have a different adiabatic exponent, <math>~\gamma_c</math>, from the envelope, <math>~\gamma_e</math>; this also means that <math>~\alpha</math> will be correspondingly different in the two regions. First, note that the ratio of the eigenfrequencies is,
|
<math>~ \frac{3\omega_e^2}{2\pi G \gamma_e \rho_e} \biggl[\frac{2\pi G \gamma_c \rho_c}{3\omega_c^2}\biggr] </math> |
<math>~=</math> |
<math>~ \frac{ 2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) }{ 2\alpha_c + 2j(2j+5) } \, , </math> |
where,
|
<math>~c_0</math> |
<math>~=</math> |
<math>~\pm\sqrt{1 + \alpha_e} - 1 \, .</math> |
So, if we want the dimensional eigenfrequencies to be identical, this means we need,
|
<math>~ \frac{\gamma_c \rho_c}{\gamma_e \rho_e} </math> |
<math>~=</math> |
<math>~ \frac{ 2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) }{ 2\alpha_c + 2j(2j+5) } </math> |
|
<math>~ \Rightarrow ~~~ \gamma_c [ 6 + 2j(2j+5)] </math> |
<math>~=</math> |
<math>~8 + \gamma_e [2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) ]\frac{\rho_e}{\rho_c} \, . </math> |
No Physical Solution11
Let's try <math>~(\ell,j) = (1,1) \, .</math> Skimming through the earlier Example11 discussion, above, it looks like the only thing we need to do in order to allow the core and envelope to have different adiabatic exponents is to explicitly add the "envelope" subscript to <math>~\alpha</math> on the right-hand side of the last expression for <math>~g^2</math>. That is, in order to match both the value and the first derivative of the two eigenfunctions at the core/envelope interface, we need,
|
<math>~ g^2 </math> |
<math>~=</math> |
<math>~\frac{7}{5}+ \frac{14}{5} \biggl[ \frac{\alpha_e -c_0(c_0+5)}{c_0[(c_0 + 3)(c_0+8) - \alpha_e ]-6(c_0+3)(c_0+4)}\biggr] </math> |
|
<math>~\Rightarrow ~~~ g^2 -1 </math> |
<math>~=</math> |
<math>~\frac{2}{5}\biggl\{1 + 7\biggl[ \frac{\alpha_e -c_0(c_0+5)}{c_0[(c_0 + 3)(c_0+8) - \alpha_e ]-6(c_0+3)(c_0+4)}\biggr] \biggr\} \, . </math> |
But, as before, the requirement that <math>~g^2 = \mathcal{B}</math> means that,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 3\biggl( \frac{\rho_e}{\rho_c}\biggr)^2 - 2\biggl( \frac{\rho_e}{\rho_c}\biggr) + (g^2-1)</math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\rho_e}{\rho_c}\biggr)</math> |
<math>~=</math> |
<math>~ \frac{1}{3} \biggl[1 \pm \sqrt{1-3(g^2-1) } \biggr] \, .</math> |
Notice that the right-hand side of this expression only depends on the choice of the adiabatic exponent in the envelope. When combined with the condition imposed by setting the dimensional frequency ratio to unity, we have,
|
<math>~ \frac{\gamma_c }{\gamma_e } </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ 2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) }{ 2\alpha_c + 2j(2j+5) }\biggr]\biggl( \frac{\rho_e}{\rho_c}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{ 2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) }{ 3[2\alpha_c + 2j(2j+5) ]} \biggl[1 \pm \sqrt{1-3(g^2-1) } \biggr] </math> |
|
<math>~\Rightarrow~~~\gamma_c 3[2\alpha_c + 2j(2j+5) ]</math> |
<math>~=</math> |
<math>~\gamma_e [2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) ] [1 \pm \sqrt{1-3(g^2-1) } ] \, . </math> |
In this last expression, the left-hand side only depends on the adiabatic exponent in the core, while the right-hand side only depends on the adiabatic exponent in the envelope.
Evaluation (Tohline's Excel spreadsheet AdExp inside workbook AnalyticEigenvector.xlsx): Over the range, <math>~-1 \le \alpha \le 3</math>, we plotted <math>~\mathrm{LHS}(\alpha_e)</math> and <math>~\mathrm{RHS}(\alpha_c)</math> for the example case of <math>~(\ell, j) = (1,1)</math>. There was a fairly wide range of pairings, <math>~(\alpha_c,\alpha_e)</math> for which the LHS = RHS; for example, at <math>~(-1, + 1.05)</math>, both sides give <math>~\approx 36</math>, and at <math>~(1.95, 1.95)</math>, both sides give <math>~\approx 200</math>. But in all cases, the inferred density ratio was greater than unity. Hence, this example index pairing does not seem to result in physically relevant core-envelope eigenvectors.
Solution21
Setup
Let's try <math>~(\ell, j) = (2,1)</math>. Examining the above, Example21 discussion, we deduce that, in order for the first derivative of both eigenfunctions to be equal at the interface, we need,
|
<math>~- a_0 \cdot \frac{14}{5} \biggl(\frac{1}{g^2}\biggr) </math> |
<math>~=</math> |
<math>~ b_0 \biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha_e}\biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ - \biggl[\frac{14}{5g^2-7} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] + \mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha_e}\biggr] \biggr\}^{-1} </math> |
|
|
|
<math>~ \times \biggl\{ c_0 + (c_0 +3)\mathcal{D} \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] </math> |
|
|
|
<math>~ + (c_0+6)\mathcal{D}^2 \biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr] \biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha_e}\biggr] \biggr\} </math> |
Notice that the core's adiabatic exponent does not explicitly enter into this condition. Given that,
|
<math>~\mathcal{D} = q^3 \, ,</math> |
and |
<math>~g^2 = (1+2\mathcal{D})^{-2} = (1+2q^3)^{-2} \, ,</math> |
|
WRONG! This relation should read,
|
we can view this expression as a conditional relationship between <math>~q</math> and <math>~\gamma_e</math>. Once a <math>~(q,\gamma_e)</math> pair has been found that satisfies this condition, we can use the matching-frequency condition to give the corresponding, required value of <math>~\gamma_c</math>; specifically, for <math>~(\ell,j) = (2,1)</math>,
|
<math>~ \gamma_c[2\alpha_c + 2j(2j+5) ]</math> |
<math>~=</math> |
<math>~ \gamma_e[2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) ]\biggl(\frac{\rho_e}{\rho_c}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \gamma_e[2\alpha_e + (c_0 + 3\ell)(c_0 + 3\ell +5) ] \biggl[\frac{2q^3}{1+2q^3}\biggr] </math> |
|
<math>~\Rightarrow~~~ \gamma_c[2(3-4/\gamma_c) + 14 ] </math> |
<math>~=</math> |
<math>~ \gamma_e [2(3 - 4/\gamma_e) + (c_0 + 6)(c_0 + 11) ] \biggl[\frac{2q^3}{1+2q^3}\biggr] </math> |
|
<math>~\Rightarrow~~~ 20\gamma_c-8 </math> |
<math>~=</math> |
<math>~ \gamma_e [6 + (c_0 + 6)(c_0 + 11) ] \biggl[\frac{2q^3}{1+2q^3}\biggr] - 8\biggl[\frac{2q^3}{1+2q^3}\biggr] </math> |
|
<math>~\Rightarrow~~~ \gamma_c </math> |
<math>~=</math> |
<math>~ \frac{1}{20}\biggl\{ \gamma_e [6 + (c_0 + 6)(c_0 + 11) ] \biggl[\frac{2q^3}{1+2q^3}\biggr] + 8\biggl[\frac{1}{1+2q^3}\biggr] \biggr\} \, . </math> |
First Few Numerically Determined Model Parameters
| Example Solutions <math>~(\ell,j) = (2,1)</math> | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Envelope | Interface | Core | |||||||||
| <math>~n_e</math> | <math>~\gamma_e</math> | <math>~\alpha_e</math> | <math>~c_0</math> (plus) | <math>~\sigma^2_{\ell=2}|_\mathrm{env}</math> | <math>~q^3</math> | <math>~\frac{\rho_e}{\rho_c}</math> | <math>~\nu</math> | <math>~n_c</math> | <math>~\gamma_c</math> | <math>~\alpha_c</math> | <math>~\sigma^2_{j=1}|_\mathrm{core}</math> |
| <math>~20</math> | <math>~1.05</math> | <math>~- 0.80956</math> | <math>~- 0.56356</math> | 55.118 | <math>~0.4564055</math> | <math>~0.4772092</math> | <math>~0.6376037</math> | <math>~1.2805786</math> | <math>~1.780897</math> | <math>~+0.7539409</math> | 15.508 |
| <math>~10</math> | <math>~1.1</math> | <math>~- 0.6363636</math> | <math>~- 0.3969773</math> | 58.136 | <math>~0.47763915</math> | <math>~0.4885639</math> | <math>~0.6517594</math> | <math>~1.0393067</math> | <math>~1.9621799</math> | <math>~+0.9614509</math> | 15.923 |
| <math>~5</math> | <math>~1.2</math> | <math>~- 1/3</math> | <math>~- 0.1835034</math> | 62.247 | <math>~0.50243157</math> | <math>~0.50121284</math> | <math>~0.6682877</math> | <math>~0.7861924</math> | <math>~2.2719532</math> | <math>~+1.2394004</math> | 16.479 |
| <math>~3</math> | <math>~4/3</math> | <math>~0</math> | <math>~0</math> | 66 | <math>~0.52185923</math> | <math>~0.51069581</math> | <math>~0.68123949</math> | <math>~0.6071418</math> | <math>~2.6470616</math> | <math>~+1.4888905</math> | 16.978 |
Note that, in all cases, we find,
|
<math>~\frac{\sigma^2|_\mathrm{env}}{\sigma^2_\mathrm{core}} \biggl(\frac{\rho_e}{\rho_c} \biggr) \frac{\gamma_e}{\gamma_c}</math> |
<math>~=</math> |
<math>~1 \, ,</math> |
thereby demonstrating that the ratio of the dimensional frequencies is unity.
Special Case of 4/3 Envelope
It is worth examining in more detail the specific case of <math>~\gamma_e = 4/3</math> because, in this case, <math>~\alpha_e</math> and <math>~c_0</math> (plus) are both zero, so the constraint equations become simpler. For this specific case, in order for the two eigenfunctions and their first derivatives to match at the interface, we have,
|
<math>~- \biggl[\frac{14(1+2q^3)^2 }{5-7(1+2q^3)^2} \biggr] </math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + q^3 \biggl[ \frac{-6\cdot 11}{3\cdot 5}\biggr] + q^6 \biggl[ \frac{- 6\cdot 11}{3\cdot 5}\biggr] \biggl[ \frac{3\cdot 8 - 6\cdot 11}{6\cdot 8} \biggr] \biggr\}^{-1} </math> |
|
|
|
<math>~ \times \biggl\{ 3q^3 \biggl[ \frac{-6\cdot 11}{3\cdot 5}\biggr] + 6q^6 \biggl[ \frac{-6\cdot 11}{3\cdot 5}\biggr] \biggl[ \frac{3\cdot 8 - 6\cdot 11}{6\cdot 8} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ q^3\biggl\{ -66 + q^3 \biggl[ \frac{6\cdot 77}{4} \biggr] \biggr\} \times \biggl\{ 5 -22q^3 + q^6 \biggl[ \frac{77}{4} \biggr] \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ 66 q^3\biggl[ \frac{-4+ 7q^3}{20 -88q^3 + 77q^6 } \biggr] </math> |
|
<math>~\Rightarrow ~~~ - [ 14(1+2q^3)^2] [20 -88q^3 + 77q^6]</math> |
<math>~=</math> |
<math>~ 66 q^3[ -4+ 7q^3 ] [5-7(1+2q^3)^2] \, . </math> |
|
<math>~\Rightarrow ~~~ 165q^3(4-7q^3)</math> |
<math>~=</math> |
<math>~ 14(1+2q^3)^2(10+22q^3 - 77q^6) \, . </math> |
In the physically relevant range of the parameter, <math>~0 < q < 1</math>, the parameter value that satisfies this constraint is,
<math>~q^3 = 0.52185923 \, .</math>
From the frequency-ratio constraint, therefore, we have,
|
<math>~ \gamma_c </math> |
<math>~=</math> |
<math>~ \frac{ 2}{5}\biggl[\frac{1+24 q^3 }{1+2q^3 }\biggr] = 2.6470616 \, .</math> |
Roots of Quartic Equation
Let,
| for <math>~\gamma_e = \frac{4}{3}</math> | ||||
|
<math>~A_{21}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{c_0(c_0+5) - (c_0 + 6)(c_0 + 11)}{(c_0 + 3)(c_0+5) - \alpha_e}\biggr]</math> |
… |
<math>~- \frac{22}{5}</math> |
|
<math>~B_{21}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{(c_0+3)(c_0+8) - (c_0 + 6)(c_0 + 11)}{(c_0 + 6)(c_0+8) - \alpha_e}\biggr] </math> |
… |
<math>~\frac{-7}{8}</math> |
Then the interface constraint equation takes the form,
|
<math>~ \frac{14(1+2\mathcal{D})^2}{7(1+2\mathcal{D})^2-5} </math> |
<math>~=</math> |
<math>~ \frac{ c_0 + (c_0 +3)\mathcal{D} A_{21} + (c_0+6)\mathcal{D}^2 A_{21} B_{21} }{ 1 + \mathcal{D} A_{21} + \mathcal{D}^2 A_{21}\cdot B_{21} } </math> |
|
<math>~\Rightarrow~~~ 7(1+4\mathcal{D} + 4\mathcal{D}^2) \cdot [2 + 2 A_{21}\mathcal{D} + 2A_{21}\cdot B_{21}\mathcal{D}^2 ] </math> |
<math>~=</math> |
<math>~ [c_0 + (c_0 +3) A_{21}\mathcal{D} + (c_0+6)A_{21}B_{21} \mathcal{D}^2 ]\cdot [7(1+4\mathcal{D} + 4\mathcal{D}^2)-5] </math> |
|
<math>~\Rightarrow~~~ -5 [c_0 + (c_0 +3) A_{21}\mathcal{D} + (c_0+6)A_{21}B_{21} \mathcal{D}^2 ] </math> |
<math>~=</math> |
<math>~ 7(1+4\mathcal{D} + 4\mathcal{D}^2) \biggl\{ [2 + 2 A_{21}\mathcal{D} + 2A_{21}\cdot B_{21}\mathcal{D}^2 ] - [c_0 + (c_0 +3) A_{21}\mathcal{D} + (c_0+6)A_{21}B_{21} \mathcal{D}^2 ]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 7(1+4\mathcal{D} + 4\mathcal{D}^2) [ (2-c_0) - (1+c_0) A_{21}\mathcal{D} - (4+c_0)A_{21}\cdot B_{21}\mathcal{D}^2 ] </math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~5 [c_0 + (c_0 +3) A_{21}\mathcal{D} + (c_0+6)A_{21}B_{21} \mathcal{D}^2 ] + 7(1+4\mathcal{D} + 4\mathcal{D}^2) [ (2-c_0) - (1+c_0) A_{21}\mathcal{D} - (4+c_0)A_{21}\cdot B_{21}\mathcal{D}^2 ] </math> |
|
|
<math>~=</math> |
<math>~[5c_0 + 5(c_0 +3) A_{21}\mathcal{D} + 5(c_0+6)A_{21}B_{21} \mathcal{D}^2 ] + [ 7(2-c_0) - 7(1+c_0) A_{21}\mathcal{D} - 7(4+c_0)A_{21}\cdot B_{21}\mathcal{D}^2 ] </math> |
|
|
|
<math>~ + [ 28(2-c_0)\mathcal{D} - 28(1+c_0) A_{21}\mathcal{D}^2 - 28(4+c_0)A_{21}\cdot B_{21}\mathcal{D}^3 ] </math> |
|
|
|
<math>~ + [ 28(2-c_0) \mathcal{D}^2 - 28(1+c_0) A_{21}\mathcal{D}^3 - 28 (4+c_0)A_{21}\cdot B_{21}\mathcal{D}^4 ] </math> |
|
<math>~</math> |
<math>~=</math> |
<math>~ \mathcal{D}^0[5c_0 + 7(2-c_0) ] + \mathcal{D}^1[5(c_0 +3) A_{21} - 7(1+c_0) A_{21} + 28(2-c_0)] </math> |
|
|
|
<math>~+ \mathcal{D}^2[5(c_0+6)A_{21}B_{21} - 7(4+c_0)A_{21}\cdot B_{21} - 28(1+c_0) A_{21} + 28(2-c_0) ] + \mathcal{D}^3[- 28(4+c_0)A_{21}\cdot B_{21} - 28(1+c_0) A_{21} ] + \mathcal{D}^4[- 28 (4+c_0)A_{21}\cdot B_{21} ] </math> |
|
<math>~</math> |
<math>~=</math> |
<math>~ \mathcal{D}^0[ 14- 2c_0 ] + \mathcal{D}^1[28(2-c_0) + (8-2c_0) A_{21} ] + \mathcal{D}^2[28(2-c_0) - 28(1+c_0) A_{21} + 2(1 - c_0)A_{21}B_{21} ] </math> |
|
|
|
<math>~+ \mathcal{D}^3[(1+c_0) + (4+c_0)B_{21} ] (-28A_{21}) + \mathcal{D}^4[- 28 (4+c_0)A_{21}\cdot B_{21} ] \, . </math> |
To solve this equation analytically, we follow the Summary of Ferrari's method that is presented in Wikipedia's discussion of the Quartic Function to identify the roots of an arbitrary quartic equation.
|
First, we adopt the shorthand notation:
where, in our particular case,
Now, define,
Then the four roots of the quartic equation are,
The <math>~\Chi_1</math> root is the physically relevant one, and it matches the interface value of <math>~\mathcal{D} = q^3</math> associated with <math>~\gamma_e = 4/3</math> in our above table of example solutions. Excellent! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In summary then, for any choice of the envelope's adiabatic exponent, <math>~\gamma_e</math>, the physically relevant root of the quartic equation gives us the interface location of the model for which our analytically specified eigenvector applies; specifically,
<math>~q = \Chi_1^{1/3} \, .</math>
From this value, we also know that,
<math>~ g = \frac{1}{(1+2q^3)} \, ; </math> <math>~ \frac{\rho_e}{\rho_c} = \frac{2q^3}{(1+2q^3)} \, ; </math> and <math>~ \nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} = \biggl[3\biggr(1 - \frac{\rho_e}{\rho_c}\biggr)\biggr]^{-1} \, . </math>
|
WRONG! The first of these three expressions should read,
|
Combined Eigenfunction
From above, we know that the eigenfunction for the core <math>~(0 \le \xi \le 1)</math> is,
|
<math>~x_{j=1} |_\mathrm{core}</math> |
<math>~=</math> |
<math>~a_0\biggl[1 - \frac{7}{5} \biggl(\frac{\xi}{g}\biggr)^2 \biggr] = \frac{5 - 7 (1+2q^3)^2 \xi^2}{5-7(1+2q^3)^2} \, .</math> |
And the matching eigenfunction for the envelope <math>~(1 \le \xi \le q^{-1})</math> is,
|
<math>~x_{\ell=2} |_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \xi^{c_0}\biggl[ \frac{ 1 + q^3 A_{21} \xi^{3} + q^6 A_{21}B_{21}\xi^{6} }{ 1 + q^3 A_{21} + q^6 A_{21}B_{21}}\biggr] \, . </math> |
Related Discussions
- Summary of Above, Detailed Derivation
- Searching for Additional, Analytically Specified Eigenvectors of Zero-Zero Bipolytropes

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |