User:Tohline/SSC/IsothermalSimilaritySolution
Similarity Solution
Much of the material in this chapter has been drawn from §4.1 of a review article by Tohline (1982) titled, Hydrodynamic Collapse.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Several authors (references given, below) have shown that when isothermal pressure gradients are important during a gas cloud's collapse, the equations governing the collapse admit a set of similarity solutions. Certain properties of these solutions can be described analytically and are instructive models for comparison with more detailed, numerical collapse calculations.
Establishing Set of Governing Equations
Drawing from an accompanying chapter's introductory discussion, we begin with the set of governing equations that describe the collapse of isothermal spheres from an Eulerian frame of reference.
| Eulerian Frame | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Notice that, following Larson's (1969) lead, we have replaced the standard continuity equation with the following equivalent statement of mass conservation:
|
<math>~\frac{dM_r}{dt}</math> |
<math>~=</math> |
<math>~0 </math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~\frac{\partial M_r}{\partial t} + v_r ~\frac{\partial M_r}{\partial r} </math> |
|
|
<math>~=</math> |
<math>~\frac{\partial M_r}{\partial t} +4\pi r^2 \rho v_r \, .</math> |
Mathematical Solution
Summary
A similarity solution becomes possible for these equations when the single independent variable,
<math>~\zeta = \frac{c_s t}{r} \, ,</math>
is used to replace both <math>~r</math> and <math>~t</math>. Then, if <math>~M_r</math>, <math>~\rho</math>, and <math>~v_r</math> assume the following forms,
|
<math>~M_r(r,t)</math> |
<math>~=</math> |
<math>~\biggl(\frac{c_s^3 t}{G}\biggr) m(\zeta) \, ,</math> |
|
<math>~\rho(r,t)</math> |
<math>~=</math> |
<math>~\biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \, ,</math> |
|
<math>~v_r(r,t)</math> |
<math>~=</math> |
<math>~- c_s U(\zeta) \, ,</math> |
the three coupled partial differential equations reduce to two coupled ordinary differential equations for the functions, <math>~\Rho (\zeta)</math> and <math>~U(\zeta)</math>, namely,
|
<math>~\frac{dU}{d\zeta}</math> |
<math>~=</math> |
<math>~ \frac{(\zeta U +1) [\Rho (\zeta U +1) -2)]}{[ (\zeta U +1)^2 - \zeta^2]} \, , </math> |
|
<math>~\frac{dP}{d\zeta}</math> |
<math>~=</math> |
<math>~\frac{\zeta \Rho [2-\Rho (\zeta U +1)]}{[ (\zeta U +1)^2 - \zeta^2]} \, ,</math> |
and a single equation defining <math>~m(\zeta)</math>,
|
<math>~m(\zeta)</math> |
<math>~=</math> |
<math>~\Rho \biggl[ U + \frac{1}{\zeta} \biggr] \, .</math> |
The parameters <math>~\zeta, m, \Rho</math>, and <math>~U</math>, and this summary set of equations are exactly those used by Hunter (1977) in his analysis of this problem. But they differ in form from the relations used by Larson (1969), Penston (1969), and Shu (1977) primarily because these authors chose to use a similarity variable,
<math>~x = \pm \frac{1}{\zeta} \, ,</math>
instead of <math>~\zeta</math>. Hunter's analysis is the most complete and his relations will be used here, but a transformation between his presentation and those of the other authors can be easily obtained from Table 1 of Hunter (1977) which, for convenience, is reproduced here.
|
Analogous to Table 1 from Hunter (1977) |
||||
|---|---|---|---|---|
| Physical Quantity |
Herein | Larson (1969) | Penston (1969) | Shu (1977) |
| <math>~\frac{c_s t}{r}</math> | <math>~\zeta</math> | <math>~- \frac{1}{x}</math> | <math>~- \frac{1}{x}</math> | <math>~+ \frac{1}{x}</math> |
| <math>~- \frac{v_r}{c_s}</math> | <math>~U</math> | <math>~\xi</math> | <math>~- V</math> | <math>~-v</math> |
| <math>~\frac{4\pi G\rho r^2}{c_s^2}</math> | †<math>~\Rho</math> | <math>~x^2\eta</math> | <math>~x^2 e^Q</math> | <math>~x^2\alpha</math> |
| <math>~\frac{GM_r}{c_s^3 t}</math> | <math>~m</math> | … | <math>~-N</math> | <math>~m</math> |
| <math>~\ln(4\pi G\rho t^2)</math> | <math>~Q</math> | <math>~\ln\eta</math> | <math>~Q</math> | <math>~\ln\alpha</math> |
| <math>~\frac{r}{(- c_s t)}</math> | <math>~y</math> | <math>~x</math> | <math>~x</math> | <math>~-x</math> |
|
†Adopting Hunter's notation, this dimensionless variable name, <math>~\Rho</math> (the capital Greek letter, <math>~\rho</math>), should not be confused with the variable name, <math>~P</math>, that represents herein the ideal gas pressure. |
||||
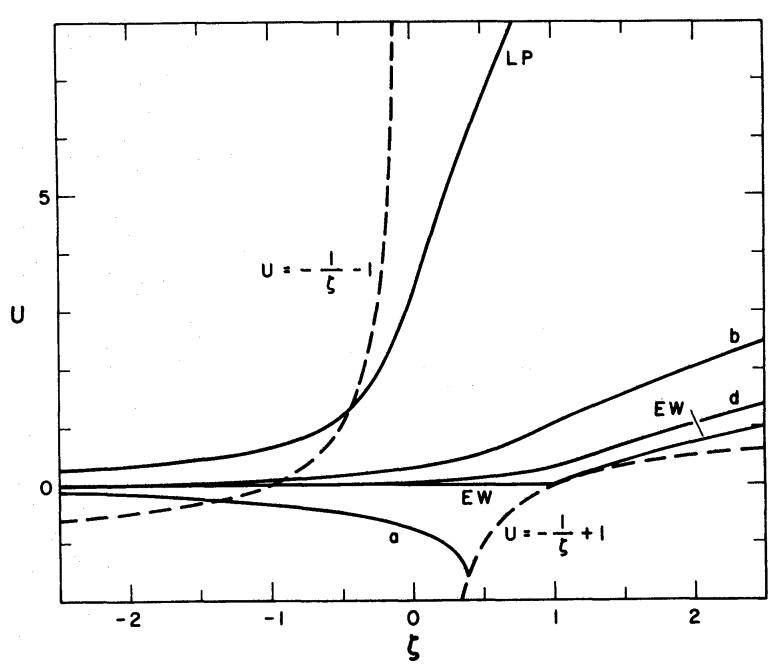
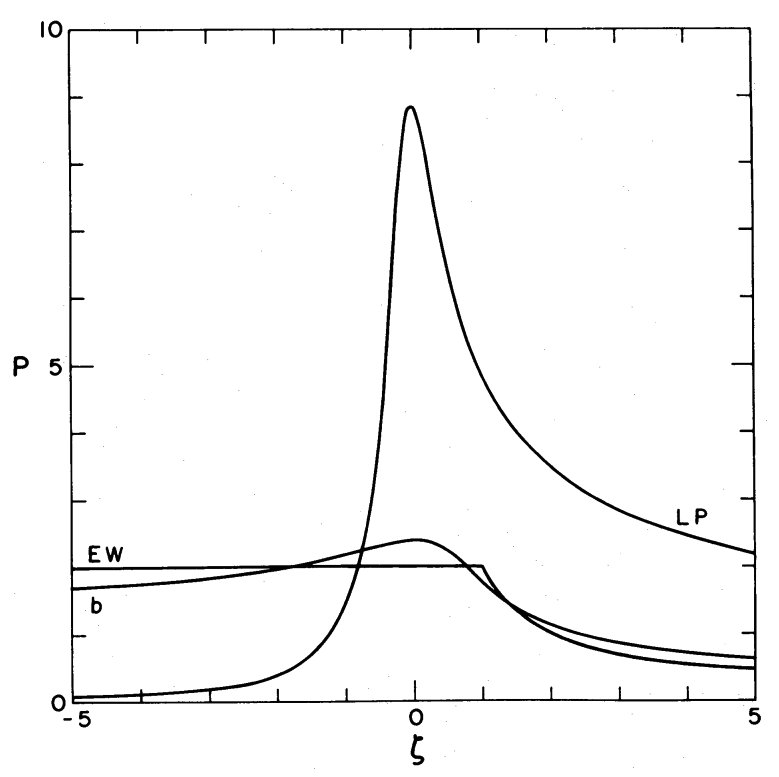
The following pair of images are reproductions of (left) Figure 1 and (right) Figure 3 from Hunter (1977). The solid curves show how (left) the dimensionless velocity, <math>~U</math>, and (right) the dimensionless density, <math>~\Rho</math>, behave as a function of the similarity variable, <math>~\zeta</math>, for models having several different prescribed values of Hunter's parameter, <math>~Q_0</math>. For each value of <math>~Q_0</math>, the table of numbers immediately below the pair of images provides corresponding values of several other numerical constants.
|
Figures extracted from Hunter (1977)
"The Collapse of Unstable Isothermal Spheres"
ApJ, vol. 218, pp. 834 - 845 © American Astronomical Society | ||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
Proof
Plugging the similarity solution expressions for <math>~M_r</math> and <math>~\rho</math> into the first of the three governing equations gives,
|
<math>~\frac{\partial}{\partial r} \biggl[ \biggl(\frac{c_s^3 t}{G}\biggr) m(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~4\pi r^2 \biggl[ \biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \biggr] </math> |
|
<math>~\Rightarrow ~~~ (c_s t ) \frac{\partial}{\partial r} \biggl[ m(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~\Rho (\zeta) \, .</math> |
Plugging the similarity solution expressions for <math>~M_r</math>, <math>~\rho</math>, and <math>~v_r</math> into the second of the three governing equations gives,
|
<math>~\frac{\partial}{\partial t} \biggl[ \biggl(\frac{c_s^3 t}{G}\biggr) m(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~- 4\pi r^2 \biggl[ \biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \biggr] \biggl[ -c_s U(\zeta)\biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{\partial}{\partial t} \biggl[ t m(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~\Rho (\zeta) U(\zeta) </math> |
|
<math>~\Rightarrow ~~~ m(\zeta) + t \biggl[ \frac{\partial m(\zeta)}{\partial t} \biggr]</math> |
<math>~=</math> |
<math>~\Rho (\zeta) U(\zeta) \, .</math> |
And, plugging the similarity solution expressions for <math>~M_r</math>, <math>~\rho</math>, and <math>~v_r</math> into the third of the three governing equations gives,
|
<math>~\frac{\partial }{\partial t} \biggl[ - c_s U(\zeta) \biggr] + \biggl[ - c_s U(\zeta) \biggr] \frac{\partial }{\partial r} \biggl[ - c_s U(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~- c_s^2 \biggl[\biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \biggr]^{-1} \frac{\partial }{\partial r}\biggl[ \biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \biggr] - \frac{G}{r^2}\biggl[ \biggl(\frac{c_s^3 t}{G}\biggr) m(\zeta) \biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial }{\partial t} \biggl[ U(\zeta) \biggr] - c_s U(\zeta) \frac{\partial }{\partial r} \biggl[ U(\zeta) \biggr]</math> |
<math>~=</math> |
<math>~\biggl[ \frac{c_s r^2}{\Rho (\zeta)} \biggr]\frac{\partial }{\partial r}\biggl[ \biggl(\frac{\Rho (\zeta)}{r^2}\biggr) \biggr] + \biggl[ \frac{c_s^2 t}{r^2} \biggr] m(\zeta) </math> |
|
<math>~\Rightarrow ~~~ \frac{\partial U}{\partial t} - (c_s U) \frac{\partial U}{\partial r} </math> |
<math>~=</math> |
<math>~\frac{c_s}{\Rho} \biggl[ \biggl( \frac{\partial \Rho}{\partial r}\biggr) -\frac{2\Rho}{r} \biggr] + \biggl[ \frac{c_s^2 t}{r^2} \biggr] m(\zeta) \, .</math> |
Now, from the functional dependence of <math>~m(\zeta)</math> on <math>~\Rho(\zeta)</math> and <math>~U(\zeta)</math>, we have,
|
<math>~\frac{\partial m}{\partial r}</math> |
<math>~=</math> |
<math>~ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial r} + \Rho \biggl[ \frac{\partial U}{\partial r} - \frac{1}{\zeta^2} \frac{\partial \zeta}{\partial r}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial r} + \Rho \biggl[ \frac{\partial U}{\partial r} + \frac{1}{r \zeta} \biggr] \, , </math> |
and,
|
<math>~\frac{\partial m}{\partial t}</math> |
<math>~=</math> |
<math>~ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial t} + \Rho \biggl[ \frac{\partial U}{\partial t} - \frac{1}{\zeta^2} \frac{\partial \zeta}{\partial t}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial t} + \Rho \biggl[ \frac{\partial U}{\partial t} - \frac{1}{t \zeta} \biggr] \, . </math> |
Hence, the first two governing equations become, respectively,
|
<math>~\Rho </math> |
<math>~=</math> |
<math>~(r\zeta) \biggl\{ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial r} + \Rho \biggl[ \frac{\partial U}{\partial r} + \frac{1}{r \zeta} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ r\zeta U + r \biggr] \frac{\partial\Rho}{\partial r} + (r\zeta \Rho ) \frac{\partial U}{\partial r} + \Rho </math> |
|
<math>~\Rightarrow~~~0</math> |
<math>~=</math> |
<math>~ \biggl[ \zeta U + 1\biggr] \frac{\partial\Rho}{\partial r} + (\zeta \Rho ) \frac{\partial U}{\partial r} \, ; </math> |
|
<math>~\Rho (\zeta) U(\zeta)</math> |
<math>~=</math> |
<math>~ \Rho\biggl[ U + \frac{1}{\zeta}\biggr] + t \biggl\{ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial t} + \Rho \biggl[ \frac{\partial U}{\partial t} - \frac{1}{t \zeta} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~0</math> |
<math>~=</math> |
<math>~ t \biggl\{ \biggl[ U + \frac{1}{\zeta} \biggr] \frac{\partial\Rho}{\partial t} + \Rho \biggl[ \frac{\partial U}{\partial t} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~0</math> |
<math>~=</math> |
<math>~ \biggl[ \zeta U + 1 \biggr] \frac{\partial\Rho}{\partial t} + (\zeta \Rho) \frac{\partial U}{\partial t} \, . </math> |
Now, we can use these two relations to replace derivatives of <math>~\Rho</math> with derivatives of <math>~U</math> — or visa versa — in the third governing relation. In the first case, we obtain,
|
<math>~ \frac{\Rho}{c_s} \biggl[\frac{\partial U}{\partial t} - (c_s U) \frac{\partial U}{\partial r} \biggr]</math> |
<math>~=</math> |
<math>~\biggl( \frac{\partial \Rho}{\partial r}\biggr) -\frac{2\Rho}{r} + \frac{\Rho^2}{r} \biggl[\zeta U + 1\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\Rho^2(\zeta U + 1)}{r} -\frac{2\Rho}{r} - \biggl( \frac{\partial U}{\partial r}\biggr) \biggl[ \frac{\zeta \Rho}{(\zeta U + 1)} \biggr]</math> |
|
<math>~ \Rightarrow ~~~ \frac{1}{r} \biggl[ \Rho^2(\zeta U + 1) - 2\Rho \biggr] </math> |
<math>~=</math> |
<math>~ \frac{\Rho}{c_s} \biggl[\frac{\partial U}{\partial t}\biggr] - (\Rho U) \frac{\partial U}{\partial r} + \biggl( \frac{\partial U}{\partial r}\biggr) \biggl[ \frac{\zeta \Rho}{(\zeta U + 1)} \biggr] </math> |
|
<math>~ \Rightarrow ~~~ \biggl[ \Rho(\zeta U + 1) - 2 \biggr] </math> |
<math>~=</math> |
<math>~ \frac{r}{c_s} \biggl[\frac{\partial U}{\partial t}\biggr] + \biggl( \frac{\partial U}{\partial r}\biggr) \biggl[ \frac{r \zeta }{(\zeta U + 1)} - (rU) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{t}{\zeta} \biggl[\frac{\partial U}{\partial t}\biggr] + r \biggl( \frac{\partial U}{\partial r}\biggr) \biggl[ \frac{\zeta - U (\zeta U + 1)}{(\zeta U + 1)} \biggr] \, . </math> |
And, given that,
|
<math>~\frac{\partial U}{\partial t}</math> |
<math>~=</math> |
<math>~\biggl( \frac{dU}{d\zeta} \biggr) \frac{\partial \zeta}{\partial t} = \biggl( \frac{dU}{d\zeta} \biggr)\frac{c_s}{r} = \biggl( \frac{dU}{d\zeta} \biggr)\frac{\zeta}{t} \, ;</math> |
| and | ||
|
<math>~\frac{\partial U}{\partial r}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{dU}{d \zeta} \biggr) \frac{\partial \zeta}{\partial r} = - \frac{c_s t}{r^2} \biggl( \frac{dU}{d \zeta} \biggr) = -\frac{\zeta^2}{c_st} \biggl( \frac{dU}{d \zeta} \biggr) \, ,</math> |
we can rewrite this as an ODE of the form,
|
<math>~ \biggl[ \Rho(\zeta U + 1) - 2 \biggr] </math> |
<math>~=</math> |
<math>~ \biggl(\frac{d U}{d\zeta}\biggr) -\zeta \biggl( \frac{d U}{d\zeta }\biggr) \biggl[ \frac{\zeta - U (\zeta U + 1)}{(\zeta U + 1)} \biggr] </math> |
|
<math>~\Rightarrow ~~~ [ \Rho(\zeta U + 1) - 2 ](\zeta U + 1) </math> |
<math>~=</math> |
<math>~ \biggl(\frac{d U}{d\zeta}\biggr) \biggl\{(\zeta U + 1) -\zeta \biggl[ \zeta - U (\zeta U + 1) \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{d U}{d\zeta}\biggr) \biggl[ \zeta^2U^2 + 2\zeta U + 1 - \zeta^2 \biggr] </math> |
|
<math>~ \Rightarrow ~~~ \frac{d U}{d\zeta} </math> |
<math>~=</math> |
<math>~ \frac{ [\Rho(\zeta U + 1) - 2 ](\zeta U + 1)}{ [ (\zeta U + 1)^2 - \zeta^2 ] } \, .</math> |
In the second case, we obtain,
|
<math>~\frac{c_s}{\Rho} \biggl( \frac{\partial \Rho}{\partial r}\biggr) + \frac{\zeta}{t} \biggl[ \Rho (\zeta U + 1 ) - 2\biggr] </math> |
<math>~=</math> |
<math>~ \frac{\partial U}{\partial t} - (c_s U) \frac{\partial U}{\partial r} </math> |
|
|
<math>~=</math> |
<math>~ -\biggl[ \frac{\zeta U +1}{\zeta \Rho} \biggr] \frac{\partial \Rho}{\partial t} + (c_s U) \biggl[ \frac{\zeta U + 1}{\zeta\Rho} \biggr] \frac{\partial \Rho}{\partial r} </math> |
|
<math>~\Rightarrow ~~~ \frac{\zeta}{t} \biggl[ 2- \Rho (\zeta U + 1 ) \biggr] </math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{c_s}{\Rho} - (c_s U) \biggl[ \frac{\zeta U + 1}{\zeta\Rho} \biggr] \biggr\}\frac{\partial \Rho}{\partial r} + \biggl[ \frac{\zeta U +1}{\zeta \Rho} \biggr] \frac{\partial \Rho}{\partial t} </math> |
|
<math>~\Rightarrow ~~~ \frac{\zeta^2 \Rho}{c_s t} \biggl[ 2- \Rho (\zeta U + 1 ) \biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ \zeta - U (\zeta U + 1 ) \biggr] \frac{\partial \Rho}{\partial r} + \frac{1}{c_s}\biggl[ \zeta U +1 \biggr] \frac{\partial \Rho}{\partial t} \, . </math> |
And, given that,
|
<math>~\frac{\partial \Rho}{\partial t}</math> |
<math>~=</math> |
<math>~\biggl( \frac{d\Rho}{d\zeta} \biggr) \frac{\partial \zeta}{\partial t} = \biggl( \frac{d\Rho}{d\zeta} \biggr)\frac{c_s}{r} = \biggl( \frac{d\Rho}{d\zeta} \biggr)\frac{\zeta}{t} \, ;</math> |
| and | ||
|
<math>~\frac{\partial \Rho}{\partial r}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{d\Rho}{d \zeta} \biggr) \frac{\partial \zeta}{\partial r} = - \frac{c_s t}{r^2} \biggl( \frac{d\Rho}{d \zeta} \biggr) = -\frac{\zeta^2}{c_st} \biggl( \frac{d\Rho}{d \zeta} \biggr) \, ,</math> |
we can rewrite this as an ODE of the form,
|
<math>~ \frac{\zeta^2 \Rho}{c_s t} \biggl[ 2- \Rho (\zeta U + 1 ) \biggr] </math> |
<math>~=</math> |
<math>~ - \frac{\zeta^2}{c_s t} \biggl[ \zeta - U (\zeta U + 1 ) \biggr] \frac{d\Rho}{d \zeta} + \frac{\zeta}{c_s t}\biggl[ \zeta U +1 \biggr] \frac{d\Rho}{d\zeta} </math> |
|
<math>~\Rightarrow~~~ \zeta\Rho [ 2- \Rho (\zeta U + 1 ) ] </math> |
<math>~=</math> |
<math>~ - \zeta\biggl[ \zeta - U (\zeta U + 1 ) \biggr] \frac{d\Rho}{d \zeta} + \biggl[ \zeta U +1 \biggr] \frac{d\Rho}{d \zeta} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{( \zeta U +1 ) - \zeta [ \zeta - U (\zeta U + 1 ) ] \biggr\} \frac{d\Rho}{d \zeta} </math> |
|
|
<math>~=</math> |
<math>~ [(\zeta U + 1)^2 - \zeta^2]\frac{d\Rho}{d \zeta} </math> |
|
<math>~ \Rightarrow~~~ \frac{d\Rho}{d \zeta} </math> |
<math>~=</math> |
<math>~ \frac{ \zeta\Rho [ 2- \Rho (\zeta U + 1 ) ] }{[(\zeta U + 1)^2 - \zeta^2] } \, . </math> |
Thus, we are able to understand the origin of the pair of 1st-order ODEs, given above, that describe the connected relationship between the two quantities, <math>~\Rho</math> and <math>~U</math>.
Limiting Behavior
It can be shown by analytic manipulation of the pair of coupled ODEs that the dimensionless density, <math>~\Rho</math>, and the dimensionless radial velocity, <math>~U</math>, have the following behaviors in various limits:
- As, <math>\zeta \rightarrow - \infty</math>:
| <math>~U \approx \frac{2}{3} \biggl( - \frac{1}{\zeta}\biggr) + \frac{1}{45} \biggl[ \frac{2}{3} - e^{Q_0}\biggr] \biggl( - \frac{1}{\zeta}\biggr)^3 \, ,</math>
|
| <math>~Q \equiv \ln(\zeta^2 \Rho) \approx Q_0 + \frac{1}{6}\biggr[ \frac{2}{3} - e^{Q_0}\biggr] \biggl( - \frac{1}{\zeta}\biggr)^2 \, ,</math>
|
| where, <math>~Q_0</math> is a positive constant. |
- For, <math>\zeta \approx 0</math>:
| <math>~U \approx U_0 + \zeta(\Rho_0 - 2)+ \zeta^2 U_0 + \zeta^3\biggl[(\Rho_0-2)(1-\Rho_0/6) - \frac{2}{3} U_0^2 \biggr] \, ,</math>
|
| <math>~\Rho \approx \Rho_0 - \zeta^2\biggl[\frac{1}{2} \Rho_0(\Rho_0 -2)\biggr] + \frac{1}{3} \zeta^3 U_0 \Rho_0(\Rho_0-4) \, ,</math>
|
| where, <math>~U_0</math> and <math>~\Rho_0</math> are positive constants. |
- As, <math>\zeta \rightarrow + \infty</math>:
| <math>~U \approx (2m_0 \zeta)^{1 / 2} \, ,</math>
|
| <math>~\Rho \approx \biggl( \frac{m_0}{2\zeta} \biggr)^{1 / 2} \, ,</math>
|
| where, <math>~m_0</math> is a positive constant. |
The values of the three constants, <math>~U_0</math>, <math>~\Rho_0</math>, and <math>~m_0</math> depend on the chosen value of <math>~Q_0</math>, as demonstrated by Hunter (1977). In terms of the physical quantities, <math>~v_r(r,t)</math> and <math>~\rho(r,t)</math>, these asymptotic behaviors translate into the following.
- For, <math>~t < 0</math> and <math>~r \ll c_s|t|</math>:
| <math>~v_r(r,t) \approx - \frac{2r}{3(-t)} \, ,</math>
|
| <math>~\rho(r,t) \approx \biggl[\frac{e^{Q_0}}{4\pi G}\biggr] \frac{1}{t^2} \, .</math>
|
- For, <math>~r \gg c_s|t|</math> at any time:
| <math>~v_r(r,t) \approx - c_s U_0\, ,</math>
|
| <math>~\rho(r,t) \approx \biggl[\frac{c_s^2 \Rho_0}{4\pi G}\biggr] \frac{1}{r^2} \, .</math>
|
- For, <math>~t > 0</math> and <math>~r \ll c_s|t|</math>:
| <math>~v_r(r,t) \approx - \biggl( \frac{2m_0}{c_s} \biggr)^{1 / 2} \biggl( \frac{t}{r}\biggr)^{1 / 2} \, ,</math>
|
| <math>~\rho(r,t) \approx \frac{1}{4\pi G} \biggl[\frac{m_0 c_s^2}{2}\biggr]^{1 / 2} \biggl( \frac{1}{t r^3}\biggr)^{1 / 2} \, .</math>
|
Examine Connection With …
Let's examine whether or not there is overlap between the properties of the above-discussed similarity solutions that give insight into the nonlinear dynamical behavior of collapse and the (a) known structure of the unperturbed, but marginally unstable Bonnor-Ebert sphere, and (b) eigenfunction that describes the radial profile of the marginally unstable radial pulsation mode. Keep in mind that, as we have presented separately, the truncation radius of the marginally unstable, Bonnor-Ebert sphere has, <math>~\xi_e \approx 6.4510534</math>.
Pressure-Truncated Equilibrium Structure
From our separate discussion of pressure-truncated isothermal spheres, we can identify the following structural properties of the marginally unstable Bonnor-Ebert sphere. The function, <math>~\psi(\xi)</math> satisfies the,
Isothermal Lane-Emden Equation
|
Given the system's sound speed, <math>~c_s</math>, and total mass, <math>~M_{\xi_e}</math>, the expression from our presentation that shows how the bounding external pressure, <math>~P_e</math>, depends on the dimensionless Lane-Emden function, <math>~\psi</math>, is,
|
<math>~P_e</math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^8}{4\pi G^3 M_{\xi_e}^2} \biggr) ~\xi_e^4 \biggl(\frac{d\psi}{d\xi}\biggr)^2_e e^{-\psi_e} \, ;</math> |
and, our expression for the truncated configuration's equilibrium radius is,
|
<math>~R</math> |
<math>~=</math> |
<math>~\frac{GM_{\xi_e}}{c_s^2} \biggl[ \xi \biggl(\frac{d\psi}{d\xi}\biggr) \biggr]_e^{-1} \, .</math> |
Also, as has been summarized in our accompanying discussion, expressions that describe the general run of radius, pressure, and mass are, respectively,
|
<math>~r_0 </math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi \, ;</math> |
|
<math>~P_0 = c_s^2 \rho_0 </math> |
<math>~=</math> |
<math>~(c_s^2 \rho_c) e^{-\psi} \, ;</math> |
|
<math>~M_r </math> |
<math>~=</math> |
<math>~\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] \, .</math> |
Hence, for isothermal configurations,
|
<math>~g_0 \equiv \frac{GM_r}{r_0^2}</math> |
<math>~=</math> |
<math>~G\biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] \biggl[ \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi\biggr]^{-2}</math> |
|
|
<math>~=</math> |
<math>~c_s^2 \biggl( \frac{4\pi G \rho_c}{c_s^2} \biggr)^{1 / 2} \biggl( \frac{d\psi}{d\xi} \biggr) \, . </math> |
From the above summary of the Hunter (1977) similarity variables, we also have, A similarity solution becomes possible for these equations when the single independent variable,
<math>~\zeta = \frac{c_s t}{r} \, ,</math>
is used to replace both <math>~r</math> and <math>~t</math>. Then, if <math>~M_r</math>, <math>~\rho</math>, and <math>~v_r</math> assume the following forms,
|
<math>~M_r(r,t)</math> |
<math>~=</math> |
<math>~\biggl(\frac{c_s^3 t}{G}\biggr) m(\zeta) \, ,</math> |
|
<math>~\rho(r,t)</math> |
<math>~=</math> |
<math>~\biggl(\frac{c_s^2 }{4\pi G r^2}\biggr) \Rho (\zeta) \, ,</math> |
|
<math>~v_r(r,t)</math> |
<math>~=</math> |
<math>~- c_s U(\zeta) \, .</math> |
Defining a new, dimensionless time as,
<math>~\tau \equiv (4\pi G \rho_c t^2)^{1 / 2} \, ,</math>
then inserting the equilibrium structures into the expressions for the similarity variables gives, for example,
|
<math>~m(\zeta)</math> |
<math>~=</math> |
<math>~ \biggl(\frac{G}{c_s^3 t}\biggr) \biggl( \frac{c_s^6}{4\pi G^3 \rho_c} \biggr)^{1/2} \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{1}{\tau}\biggr) \biggl[ \xi^2 \frac{d\psi}{d\xi} \biggr] \, ; </math> |
and,
|
<math>~\Rho (\zeta) </math> |
<math>~=</math> |
<math>~\biggl(\frac{4\pi G r^2}{c_s^2 }\biggr) \rho_c e^{-\psi} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\tau^2}{\zeta^2 }\biggr] e^{-\psi} \, ,</math> |
while,
|
<math>~\frac{1}{\zeta}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{1}{c_s t}\biggr) \biggl( \frac{c_s^2}{4\pi G \rho_c} \biggr)^{1/2} \xi </math> |
|
|
<math>~=</math> |
<math>~ \frac{\xi }{\tau} \, . </math> |
Putting these last two expressions together also gives,
|
<math>~\Rho (\zeta) </math> |
<math>~=</math> |
<math>~\xi^2 e^{-\psi} \, .</math> |
Yabushita's Radial Pulsation Eigenvector
As we have, separately, discussed in detail, the eigenvalue problem is defined in terms of the following perturbed variables,
|
<math>~P(m,t)</math> |
<math>~=</math> |
<math>~P_0(m) + P_1(m,t) = P_0(m) \biggl[1 + p(m) e^{i\omega t} \biggr] \, ,</math> |
|
<math>~\rho(m,t)</math> |
<math>~=</math> |
<math>~\rho_0(m) + \rho_1(m,t) = \rho_0(m) \biggl[1 + d(m) e^{i\omega t} \biggr] \, ,</math> |
|
<math>~r(m,t)</math> |
<math>~=</math> |
<math>~r_0(m) + r_1(m,t) = r_0(m) \biggl[1 + x(m) e^{i\omega t} \biggr] \, ,</math> |
And the following three linearized equations describe the physical relationship between the three dimensionless perturbation amplitudes <math>~p(r_0)</math>, <math>~d(r_0)</math> and <math>~x(r_0)</math>, for various characteristic eigenfrequencies, <math>~\omega</math>:
|
Linearized Linearized Linearized |
And, as was first demonstrated by Yabushita (1975),
| Exact Solution to the Isothermal LAWE | ||
|
<math>~\sigma_c^2 = 0</math> |
and |
<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, .</math> |
Numerical Integration of Coupled ODEs
Let's develop a finite-difference expression that allows us to straightforwardly integrate the above pair of coupled ODEs, namely,
|
<math>~\frac{dU}{d\zeta}</math> |
<math>~=</math> |
<math>~ \frac{(\zeta U +1) [\Rho (\zeta U +1) -2 ]}{[ (\zeta U +1)^2 - \zeta^2]} \, , </math> |
|
<math>~\frac{dP}{d\zeta}</math> |
<math>~=</math> |
<math>~\frac{\zeta \Rho [2-\Rho (\zeta U +1)]}{[ (\zeta U +1)^2 - \zeta^2]} \, .</math> |
Assume that the starting values of <math>~U</math> and <math>~\Rho</math> have been provided by, for example, one of the above detailed series expansions. Let the subscript "1" denote these known values at coordinate-location, <math>~\zeta_1</math>, and let the subscript "2" denote the unknown values of <math>~U</math> and <math>~\Rho</math> at <math>~\zeta_2 = \zeta_1 + \Delta\zeta</math>. We should be able to construct a 2nd-order accurate integration scheme by treating <math>~U</math> and <math>~\Rho</math> as average values everywhere they occur on the right-hand sides of the pair of ODEs. That is,
|
<math>~\bar{U}</math> |
<math>~\rightarrow</math> |
<math>~\frac{1}{2}\biggl(U_2 + U_1 \biggr) \, ,</math> |
and |
<math>~\bar{\Rho}</math> |
<math>~\rightarrow</math> |
<math>~\frac{1}{2}\biggl(\Rho_2 + \Rho_1 \biggr) \, .</math> |
First ODE
We'll begin by using the first ODE to provide one expression for <math>~\Rho_2</math> in terms of <math>~U</math> and <math>~\Rho_1</math>. We have,
|
<math>~ \bar{\Rho} (\zeta \bar{U} +1) </math> |
<math>~=</math> |
<math>~ 2+\biggl[ \frac{ (\zeta \bar{U} +1)^2 - \zeta^2 }{ (\zeta \bar{U} +1) } \biggr]\frac{\Delta U}{\Delta\zeta} </math> |
|
<math>~\Rightarrow~~~ \Rho_2 </math> |
<math>~=</math> |
<math>~ \frac{2}{(\zeta \bar{U} +1)} \biggl\{ 2+\biggl[ \frac{ (\zeta \bar{U} +1)^2 - \zeta^2 }{ (\zeta \bar{U} +1) } \biggr]\frac{\Delta U}{\Delta\zeta} \biggr\} - P_1 \, . </math> |
|
|
<math>~=</math> |
<math>~ \frac{2}{\ell} \biggl\{ 2+\biggl[ \frac{ \ell^2 - \zeta^2 }{ \ell } \biggr]\frac{\Delta U}{\Delta\zeta} \biggr\} - P_1 \, , </math> |
where,
<math>~\ell \equiv (\zeta \bar{U} + 1)</math> <math>~\Rightarrow</math> <math>~\bar{U} =\biggl[\frac{\ell - 1}{\zeta}\biggr] \, .</math>
Second ODE
The second ODE can presumably provide a second, independent expression for <math>~\Rho_2</math> in terms of <math>~U</math> and <math>~\Rho_1</math>. In this case we have,
|
<math>~\frac{(P_2 - P_1)}{\Delta\zeta}</math> |
<math>~=</math> |
<math>~\frac{\zeta \bar{\Rho} [2-\bar{\Rho} (\zeta \bar{U} +1)]}{[ (\zeta \bar{U} +1)^2 - \zeta^2]} </math> |
|
|
<math>~=</math> |
<math>~\frac{\zeta \tfrac{1}{2}(\Rho_1 + \Rho_2) [2-\tfrac{1}{2}(\Rho_1 + \Rho_2) (\zeta \bar{U} +1)]}{[ (\zeta \bar{U} +1)^2 - \zeta^2]} </math> |
|
<math>~\Rightarrow ~~~ \frac{ 4[ (\zeta \bar{U} +1)^2 - \zeta^2]}{ \zeta \Delta\zeta} \biggl(P_2 - P_1 \biggr)</math> |
<math>~=</math> |
<math>~(\Rho_1 + \Rho_2) [4 - (\Rho_1 + \Rho_2) (\zeta \bar{U} +1)] </math> |
|
|
<math>~=</math> |
<math>~ 4(\Rho_1 + \Rho_2) - (\Rho_1^2 + 2\Rho_1\Rho_2 +\Rho_2^2) (\zeta \bar{U} +1) </math> |
|
|
<math>~=</math> |
<math>~ \Rho_2 [4 - 2\Rho_1 (\zeta \bar{U} +1) ] - \Rho_2^2 (\zeta \bar{U} +1) + [ 4\Rho_1 - \Rho_1^2 (\zeta \bar{U} +1) ] </math> |
|
<math>~\Rightarrow ~~~ 4[ (\zeta \bar{U} +1)^2 - \zeta^2] P_2 </math> |
<math>~=</math> |
<math>~ \Rho_2 [4 - 2\Rho_1 (\zeta \bar{U} +1) ]\zeta \Delta\zeta - \Rho_2^2 (\zeta \bar{U} +1)\zeta \Delta\zeta + \biggl\{ [ 4\Rho_1 - \Rho_1^2 (\zeta \bar{U} +1) ]\zeta \Delta\zeta + 4[ (\zeta \bar{U} +1)^2 - \zeta^2] P_1 \biggr\} \, . </math> |
This is a quadratic equation of the form,
|
<math>~aP_2^2 + bP_2 + c </math> |
<math>~=</math> |
<math>~0 \, ,</math> |
where,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~ (\zeta \bar{U} +1)\zeta \Delta\zeta = \ell \zeta \Delta\zeta \, ,</math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~ - \{ [4 - 2\Rho_1 (\zeta \bar{U} +1) ]\zeta \Delta\zeta - 4[ (\zeta \bar{U} +1)^2 - \zeta^2] \} = - [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ] \, ,</math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~ - \{ [ 4\Rho_1 - \Rho_1^2 (\zeta \bar{U} +1) ]\zeta \Delta\zeta + 4[ (\zeta \bar{U} +1)^2 - \zeta^2] P_1 \} = - [ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 ] \, . </math> |
The pair of roots of this equation are, then,
|
<math>~2 \ell \zeta \Delta\zeta P_2</math> |
<math>~=</math> |
<math>~ [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ] \pm \biggl\{ [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ]^2 + 4\ell \zeta \Delta\zeta[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 ] \biggr\}^{1 / 2} \, . </math> |
Or,
|
<math>~\biggl\{ \frac{2 \ell \zeta \Delta\zeta}{ [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ] } \biggr\}P_2</math> |
<math>~=</math> |
<math>~ 1 \pm \biggl\{ 1 + \frac{4\ell \zeta \Delta\zeta[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 ]}{[ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ]^2 } \biggr\}^{1 / 2} \, . </math> |
Combined
Now, before returning to the first ODE, let's write <math>~\Delta U</math> in terms of <math>~\ell</math> and, hereafter, use <math>~\ell</math> as the unknown instead of <math>~U_2</math>.
|
<math>~\Delta U \equiv U_2 - U_1</math> |
<math>~=</math> |
<math>~(2\bar{U} - U_1) - U_1</math> |
|
|
<math>~=</math> |
<math>~2\biggl[\bar{U} - U_1 \biggr]</math> |
|
|
<math>~=</math> |
<math>~2\biggl[\frac{(\ell - 1)}{\zeta} - U_1 \biggr]</math> |
Hence, the first ODE gives,
|
<math>~ \ell^2 \Rho_2 </math> |
<math>~=</math> |
<math>~ 2\biggl\{ 2\ell +\biggl[ \ell^2 - \zeta^2 \biggr]\frac{\Delta U}{\Delta\zeta} \biggr\} - \ell^2 P_1 </math> |
|
<math>~\Rightarrow~~~ \Delta\zeta \ell^2 \Rho_2 </math> |
<math>~=</math> |
<math>~ (4\ell - \ell^2 P_1)\Delta\zeta + 2( \ell^2 - \zeta^2 ) \Delta U </math> |
|
|
<math>~=</math> |
<math>~ (4\ell - \ell^2 P_1)\Delta\zeta + 4( \ell^2 - \zeta^2 ) \biggl[\frac{(\ell - 1)}{\zeta} - U_1 \biggr] </math> |
|
<math>~\Rightarrow~~~ (2 \zeta \ell^2 \Delta\zeta )\Rho_2 </math> |
<math>~=</math> |
<math>~ 2(4\ell - \ell^2 P_1) \zeta\Delta\zeta + 8( \ell^2 - \zeta^2 ) (\ell - 1 - \zeta U_1 ) \, . </math> |
Finally, using this to replace <math>~\Rho_2</math> in the second ODE expression gives,
|
<math>~ 2(4\ell - \ell^2 P_1) \zeta\Delta\zeta + 8( \ell^2 - \zeta^2 ) (\ell - 1 - \zeta U_1 ) </math> |
<math>~=</math> |
<math>~ \ell [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ] </math> |
|
|
|
<math>~ \pm \ell \biggl\{ [ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) ]^2 + 4\ell \zeta \Delta\zeta[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 ] \biggr\}^{1 / 2} </math> |
|
<math>~\Rightarrow~~~ \frac{8}{\ell} ( \ell^2 - \zeta^2 ) (\ell - 1 - \zeta U_1 ) </math> |
<math>~=</math> |
<math>~ -4 \zeta \Delta\zeta - 4( \ell^2 - \zeta^2) </math> |
|
|
|
<math>~ \pm \biggl\{ \biggl[ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) \biggr]^2 + 4\ell \zeta \Delta\zeta \biggl[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 \biggr] \biggr\}^{1 / 2} </math> |
|
<math>~\Rightarrow~~~ \frac{1}{\ell} ( \ell^2 - \zeta^2 )\biggl[ 2 (\ell - 1 - \zeta U_1 ) + \ell \biggr] + \zeta \Delta\zeta </math> |
<math>~=</math> |
<math>~ \pm \frac{1}{4} \biggl\{ \biggl[ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) \biggr]^2 + 4\ell \zeta \Delta\zeta \biggl[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 \biggr] \biggr\}^{1 / 2} </math> |
|
<math>~\Rightarrow~~~ ( \ell^2 - \zeta^2 )\biggl[ 3\ell - 2 - 2\zeta U_1 \biggr] + \ell \zeta \Delta\zeta </math> |
<math>~=</math> |
<math>~ \pm \frac{\ell}{4} \biggl\{ \biggl[ (4 - 2\Rho_1 \ell )\zeta \Delta\zeta - 4( \ell^2 - \zeta^2) \biggr]^2 + 4\ell \zeta \Delta\zeta \biggl[ ( 4\Rho_1 - \Rho_1^2 \ell )\zeta \Delta\zeta + 4( \ell^2 - \zeta^2) P_1 \biggr] \biggr\}^{1 / 2} \, . </math> |
This doesn't look particularly useful because, after squaring both sides, it is a sixth-order polynomial in <math>~\ell</math>, which generally has no analytic solution.
Key References
- M. V. Penston (1969, MNRAS, 144, 425): Dynamics of Self-Gravitating Gaseous Sphers - III. Analytic Results in the Free-Fall of Isothermal Cases
- Richard B. Larson (1969, MNRAS, 145, 271): Numerical Calculations of the Dynamics of Collapsing Proto-Star
- F. H. Shu (1977, ApJ, 214, 488-497): Self-Similar Collapse of Isothermal Spheres and Star Formation
- C. Hunter (1977, ApJ, 218, 834-845): The Collapse of Unstable Isothermal Spheres
- A. Whitworth & D. Summers (1985, MNRAS, 214, 1 - 25): Self-Similar Condensation of Spherically Symmetric Self-Gravitating Isothermal Gas Clouds

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |