Difference between revisions of "User:Tohline/ProjectsUnderway/Core Collapse Supernovae"
(Begin typing text into this new chapter) |
(→Free-Fall Collapse: Quick intro to Lynden-Bell's early contributions) |
||
| Line 6: | Line 6: | ||
==Free-Fall Collapse== | ==Free-Fall Collapse== | ||
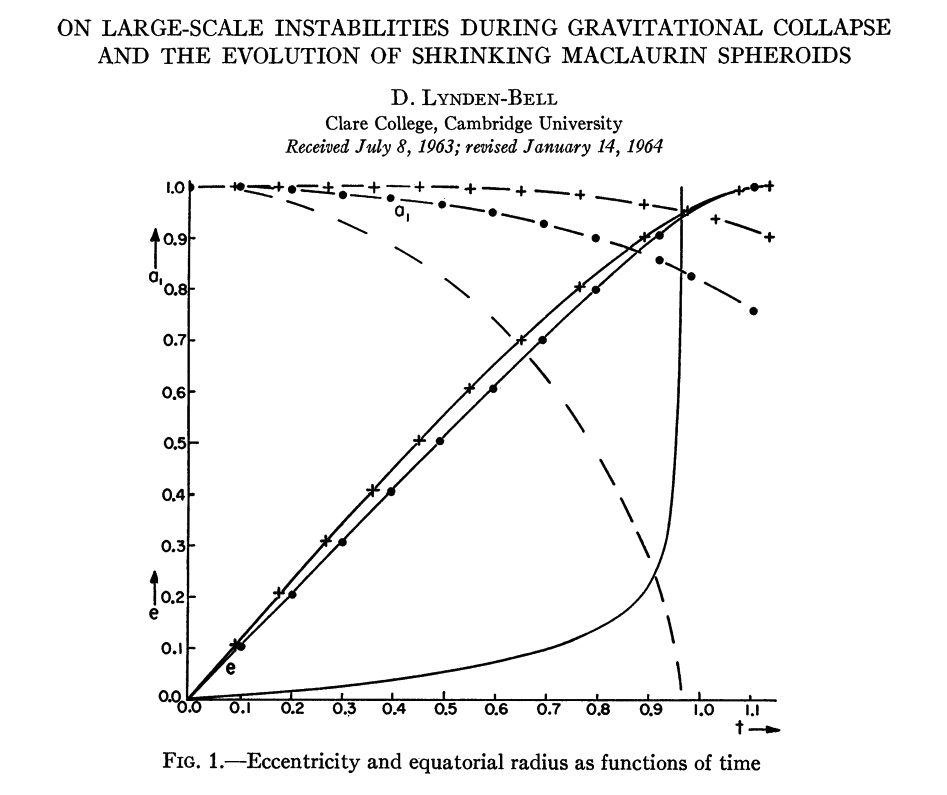
I want to begin this section by paying tribute to Donald [http://dx.doi.org.libezp.lib.lsu.edu/10.1017/S0305004100040767 Lynden-Bell (1962], Mathematical Proceedings of the Cambridge Philosophical Society, vol. 58, pp. 709-711), who was the first to appreciate the relatively simple behavior that should be exhibited by the free-fall collapse of a uniformly rotating, uniform-density spheroid. In an article less than two pages in length, Lynden-Bell first noted that the governing dynamical equations (written in cylindrical coordinates) take the form, | [[Image:LyndenBell1964.png|400px|right|Lynden-Bell (1964, ApJ, 139, 1195)]]I want to begin this section by paying tribute to Donald [http://dx.doi.org.libezp.lib.lsu.edu/10.1017/S0305004100040767 Lynden-Bell (1962], Mathematical Proceedings of the Cambridge Philosophical Society, vol. 58, pp. 709-711), who was the first to appreciate the relatively simple behavior that should be exhibited by the free-fall collapse of a uniformly rotating, uniform-density spheroid. In an article less than two pages in length, Lynden-Bell first noted that the governing dynamical equations (written in cylindrical coordinates) take the form, | ||
<div align="center"> | <div align="center"> | ||
<table border="0", cellpadding="5"> | <table border="0", cellpadding="5"> | ||
| Line 53: | Line 53: | ||
</table> | </table> | ||
</div> | </div> | ||
Then Lynden-Bell deduced that, (a) "the result of the motion is merely a change of scales"; (b) the collapsing system "remains uniform [in density], and the boundary remains spheroidal"; and (c) "the collapse … will be through a series of [uniformly rotating] spheroids." Two years later in a separate article, [http://adsabs.harvard.edu/abs/1964ApJ...139.1195L Lynden-Bell (1964], ApJ, 139, 1195) presented results from the numerical integration of this governing set of dynamical equations (see §X and Figure 1 of his article). The various publications by other authors who also have modeled the free-fall collapse of rotating or nonrotating spheroids in various contexts (see our discussion that follows) have not always acknowledged Lynden-Bell's pioneering analysis of this problem. | |||
=Related Discussions= | =Related Discussions= | ||
Revision as of 01:33, 30 August 2014
A Template for Gravitational Wave Signals from Core-Collapse Supernovae

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
29 August 2014: The initial content of this chapter has been drawn from a LaTeX document dated 23 December 2009 that J. E. Tohline created while interacting with Cody Arceneaux (at the time, an LSU undergraduate physics major) and Sarah Caudell (at the time, an LSU physics graduate student). I've decided to build on this project foundation that was laid in the 2008 - 2009 time frame.
Free-Fall Collapse
I want to begin this section by paying tribute to Donald Lynden-Bell (1962, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 58, pp. 709-711), who was the first to appreciate the relatively simple behavior that should be exhibited by the free-fall collapse of a uniformly rotating, uniform-density spheroid. In an article less than two pages in length, Lynden-Bell first noted that the governing dynamical equations (written in cylindrical coordinates) take the form,
|
<math>~\ddot{R}</math> |
<math>~=</math> |
<math>~-~ 2A_L(t) R + \frac{h_{LB}^2}{R^3} \, ,</math> |
|
<math>~\ddot{Z}</math> |
<math>~=</math> |
<math>~-~ 2C_L(t) Z \, ,</math> |
where the dots denote differentiation with respect to time, <math>~h_{LB}</math> is a constant and the two time-dependent coefficients, <math>~A(t)</math> and <math>~C(t)</math>, come from the gravitational potential that, according to Lyttleton (1953), has the form,
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~-~ 2A_L(t) R^2 ~-~ C_L(t) Z^2 \, .</math> |
Then Lynden-Bell deduced that, (a) "the result of the motion is merely a change of scales"; (b) the collapsing system "remains uniform [in density], and the boundary remains spheroidal"; and (c) "the collapse … will be through a series of [uniformly rotating] spheroids." Two years later in a separate article, Lynden-Bell (1964, ApJ, 139, 1195) presented results from the numerical integration of this governing set of dynamical equations (see §X and Figure 1 of his article). The various publications by other authors who also have modeled the free-fall collapse of rotating or nonrotating spheroids in various contexts (see our discussion that follows) have not always acknowledged Lynden-Bell's pioneering analysis of this problem.
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |