Difference between revisions of "User:Tohline/H Book"
(→Structure:: More word-smithing) |
|||
| Line 57: | Line 57: | ||
gives rise to equilibrium configurations that have a wide variety of internal structural profiles. | gives rise to equilibrium configurations that have a wide variety of internal structural profiles. | ||
If one is not particularly concerned about details regarding the distribution of matter ''within'' the equilibrium configuration, a good estimate of the size of the equilibrium system can be determined by assuming a uniform-density structure then identifying local extrema in the system's global free energy. In the astrophysics community, the mathematical relation that serves to define the properties of configurations that are associated with such free-energy extrema is often referred to as the ''scalar virial theorem''. Specifically, for ''isolated'' systems in virial equilibrium, the following relation between configuration parameters holds: | <table border="0" align="right" cellpadding="5"> | ||
<tr> | |||
<td align="center" bgcolor="white"> | |||
[[File:View3D.png|200px|right|border|Whitworth's (1981) Isothermal Free-Energy Surface]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[[User:Tohline/SSC/Virial/PolytropesEmbeddedOutline#3DIsothermalSurface|Free-Energy Surface]] | |||
</td> | |||
</tr> | |||
</table> | |||
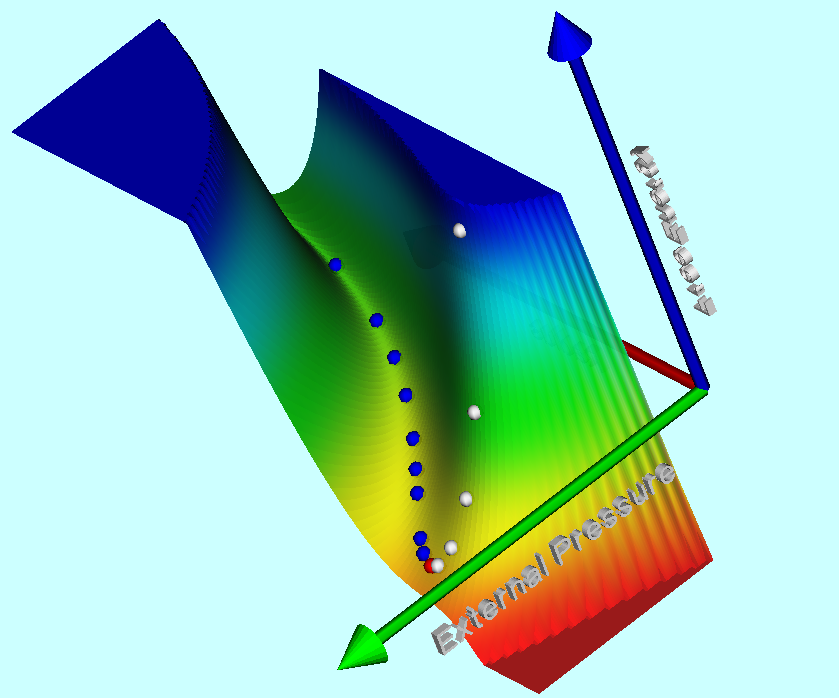
If one is not particularly concerned about details regarding the distribution of matter ''within'' the equilibrium configuration, a good estimate of the size of the equilibrium system can be determined by assuming a uniform-density structure then identifying local extrema in the system's global free energy. An illustrative, undulating free-energy surface is displayed here, on the right; blue dots identify equilibria associated with a "valley" of the free-energy surface while white dots identify equilibria that lie along a "ridge" in the free-energy surface. | |||
In the astrophysics community, the mathematical relation that serves to define the properties of configurations that are associated with such free-energy extrema is often referred to as the ''scalar virial theorem''. Specifically, for ''isolated'' systems in virial equilibrium, the following relation between configuration parameters holds: | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 75: | Line 89: | ||
</table> | </table> | ||
</div> | </div> | ||
where all three of the dimensionless ''structural form factors'', <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, are generically ''of order unity'' for detailed force-balanced models having a wide range of internal structures and are all three exactly equal to unity under the assumption that the equilibrium configuration has uniform density and uniform pressure throughout. Alternatively, if the polytropic constant, <math>~K</math> (which specifies the specific entropy of fluid elements throughout the system), instead of the central pressure, is held fixed while searching for extrema in the free-energy, the virial equilibrium relation is, | where all three of the dimensionless ''structural form factors'', <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, are generically ''of order unity'' for detailed force-balanced models having a wide range of internal structures and are all three exactly equal to unity under the assumption that the equilibrium configuration has uniform density and uniform pressure throughout. Alternatively, if the polytropic constant, <math>~K</math> (which specifies the specific entropy of fluid elements throughout the system), instead of the central pressure, is held fixed while searching for extrema in the free-energy, the virial equilibrium relation for isolated polytropes is, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 88: | Line 102: | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{3}{4\pi} \biggl(\frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr) \frac{1}{\mathfrak{f}_M} \, . | <math>~\frac{3}{4\pi} \biggl(\frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr) \frac{1}{\mathfrak{f}_M} \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 94: | Line 108: | ||
</div> | </div> | ||
If the physical system under consideration — such as a protostellar gas cloud — is not isolated but is, instead, embedded in a hot, tenuous medium that exerts on the system a confining external pressure, <math>~P_e</math>, the configuration's equilibrium parameters will be related via the expression, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 114: | Line 128: | ||
</table> | </table> | ||
</div> | </div> | ||
or, fixing <math>~K</math> instead of <math>~P_c</math>, | or, fixing <math>~K</math> instead of <math>~P_c</math>, the relevant virial equilibrium expression is, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 132: | Line 146: | ||
</table> | </table> | ||
</div> | </div> | ||
It is a virial expression specifically of this form that identifies extrema (e.g., valleys or ridges) in the rainbow-colored free-energy surface, <math>\mathfrak{G}^*(R_\mathrm{eq}, P_e)</math>, displayed above. | |||
<table border="1" width="100%" cellspacing="2" cellpadding="8"> | <table border="1" width="100%" cellspacing="2" cellpadding="8"> | ||
Revision as of 23:28, 27 February 2015
Preface from the original version of this HyperText Book (H_Book):
November 18, 1994
Much of our present, basic understanding of the structure, stability, and dynamical evolution of individual stars, short-period binary star systems, and the gaseous disks that are associated with numerous types of stellar systems (including galaxies) is derived from an examination of the behavior of a specific set of coupled, partial differential equations. These equations — most of which also are heavily utilized in studies of continuum flows in terrestrial environments — are thought to govern the underlying physics of all macroscopic "fluid" systems in astronomy. Although relatively simple in form, they prove to be very rich in nature... <more>

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Pictorial Table of Contents
Context
- Principal Governing Equations
- Continuity Equation
- Euler Equation
- <math>1^\mathrm{st}</math> Law of Thermodynamics
- Poisson Equation
Applications
Spherically Symmetric Configurations
Introduction (Alternate Introduction)
Structure:
Here we show how the set of principal governing equations (PGEs) may be solved to determine the equilibrium structure of spherically symmetric fluid configurations — such as individual, nonrotating stars. After supplementing the PGEs by specifying an equation of state of the fluid, the system of equations is usually solved by employing one of three techniques to obtain a "detailed force-balanced" model that provides the radius, <math>~R_\mathrm{eq}</math>, of the equilibrium configuration — given its mass, <math>~M</math>, and central pressure, <math>~P_c</math>, for example — as well as details regarding the internal radial profiles of the mass-density and fluid pressure. As our various discussions illustrate, simply varying the power-law index, <math>~n</math>, in a polytropic equation of state,
|
<math>~P</math> |
<math>~=</math> |
<math>~K \rho^{(n+1)/n} \, ,</math> |
gives rise to equilibrium configurations that have a wide variety of internal structural profiles.
If one is not particularly concerned about details regarding the distribution of matter within the equilibrium configuration, a good estimate of the size of the equilibrium system can be determined by assuming a uniform-density structure then identifying local extrema in the system's global free energy. An illustrative, undulating free-energy surface is displayed here, on the right; blue dots identify equilibria associated with a "valley" of the free-energy surface while white dots identify equilibria that lie along a "ridge" in the free-energy surface.
In the astrophysics community, the mathematical relation that serves to define the properties of configurations that are associated with such free-energy extrema is often referred to as the scalar virial theorem. Specifically, for isolated systems in virial equilibrium, the following relation between configuration parameters holds:
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_A \cdot \mathfrak{f}_M^2}{\mathfrak{f}_W} \, ,</math> |
where all three of the dimensionless structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, are generically of order unity for detailed force-balanced models having a wide range of internal structures and are all three exactly equal to unity under the assumption that the equilibrium configuration has uniform density and uniform pressure throughout. Alternatively, if the polytropic constant, <math>~K</math> (which specifies the specific entropy of fluid elements throughout the system), instead of the central pressure, is held fixed while searching for extrema in the free-energy, the virial equilibrium relation for isolated polytropes is,
|
<math>~\biggl( \frac{G}{K} \biggr)^n M^{n-1} R_\mathrm{eq}^{3-n}</math> |
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl(\frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr) \frac{1}{\mathfrak{f}_M} \, . </math> |
If the physical system under consideration — such as a protostellar gas cloud — is not isolated but is, instead, embedded in a hot, tenuous medium that exerts on the system a confining external pressure, <math>~P_e</math>, the configuration's equilibrium parameters will be related via the expression,
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_M^2}{\mathfrak{f}_W} \biggl[ \mathfrak{f}_A - \frac{P_e}{P_c} \biggr] \, ;</math> |
or, fixing <math>~K</math> instead of <math>~P_c</math>, the relevant virial equilibrium expression is,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr)\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
It is a virial expression specifically of this form that identifies extrema (e.g., valleys or ridges) in the rainbow-colored free-energy surface, <math>\mathfrak{G}^*(R_\mathrm{eq}, P_e)</math>, displayed above.
|
Solution Strategies: |
Detailed Force-Balance |
Virial Equilibrium |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Stability:
|
Solution Strategy Assuming Spherical Symmetry: |
|
|
Example Solutions: |
|
Dynamics:
|
Two-Dimensional Configurations
- Introduction
Structure:
|
Solution Strategies |
|
|
Example Solutions:
|
|
Stability:
Dynamics:
Three-Dimensional Configurations
Structure:
|
Solution Strategies |
|
Example Solutions:
|
Stability:
- Lou & Bai (2011, MNRAS, 415, 925) — 3D perturbations in an isothermal self-similar flow
Dynamics:
Related Projects Underway
Appendices
See Also
- NIST Digital Library of Mathematical Functions; see also the related CUP Publication

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |