User:Tohline/DarkMatter/CK2015
Remarks on Christodoulou & Kazanas (2015)
Remarks by J. E. Tohline
Date: 8 October 2015

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
First, let me say that I very much enjoyed reading this paper by Christodoulou & Kazanas (2015; hereafter CK15), which was sent to me in draft form. The first couple of times I read through the paper, I didn't get it. But then I experienced a Eureka! moment, and immediately thereafter started thinking about some key implications. In what follows, first I will comment on my Eureka! moment; then I will ramble on a bit about implications.
Building Equilibrium Models with Flat Rotation Curves
It finally dawned on me that CK15 are pointing out — what has been obvious (Ha!) to me for years — that if you want to build an equilibrium, self-gravitating configuration in which all of the equatorial-plane motions are perfectly circular, the model result will be very different if you're dealing with a gaseous configuration than if you're dealing with a stellar-dynamic system.
- In stellar-dynamic (or aged planetary!) systems, you're pretty much stuck with "Keplerian" velocity profiles; if you want to generate a flat rotation curve, you'd better modify gravity!
- But in gas-dynamical systems, radial pressure gradients can help you out big time! Indeed, you can a priori choose almost any rotation profile that you like and feel confident that you can build an equilibrium, axisymmetric configuration with that profile; the density/pressure profile will readily bend to your wishes and, as CK15 emphasize, the gravitational potential will happily tag along.
In a chapter of my online H_Book, I constructed a table that lists a wide variety of "simple rotation profiles" that have been chosen by different researchers over the years as they investigated the equilibrium and/or stability properties of a wide variety of self-gravitation gaseous configurations. So we've all "known" this for years! But, it just so happens that v = constant was almost never the choice! Hayashi, Narita, & Miyama (1982) is one exception; and that paper was exceptional because they were actually able to find an analytic solution.
Why has everyone (before CK15) chosen profiles that are not v-constant? I think the answer is that, since the equations allow you to specify virtually any profile a priori, everyone looked for a physically justified reason for picking a particular profile. Observations gave us no help because, after all, you generally can't see inside of a rotationally flattened gaseous object. Favorite choices were: Uniform rotation (a natural result of viscosity); uniform specific angular momentum (because that is the power-law limit that is marginally stable against the axisymmetric Raleigh instability); and near-Keplerian (because that gives flat disks in which pressure is not very important). There is also the so-called n' rotation profile used by Ostriker & Bodenheimer (1973) — see, for example, their §IIIa, which references equilibrium configurations with (n = 3/2, n' = 0, 1, 3/2). This example means: build a model with an n = 3/2 equation of state, but with an angular momentum profile that is the same as in a uniformly-rotating n = 0 sphere, or n = 1 sphere, or n = 3/2 sphere. Why should anyone try a v-constant profile? Until CK15(!), there was no physical justification for picking v-constant. (Except, of course, for Hayashi et al., who picked this strange profile because it allowed them to uncover an analytic description of the underlying structure.)
So, CK15 think they understand why nature picks v-constant profiles in gaseous disks. There argument is, first of all, that observations are showing us that nature likes this particular profile. It just so happens that galaxy disks are the only gaseous structures that have allowed astronomers to "see inside" the gaseous structure; and nature is saying, I am not so interested in uniform rotation, or uniform specific angular momentum, or even near-Keplerian! I like flat rotation curves! CK15 think that they know why flat rotation curves are preferred; and they are sufficiently confident in this physical reasoning to predict that young planetary disks also will reveal flat rotation curves! I wish them luck with this prediction!
VERY IMPORTANT NOTE: It is very important to appreciate that the best observations that show flat rotation curves in galaxies come from measurements of radiation from gas, and not from the underlying stars. (See comments on stellar dynamic systems below.) The radio observations are measuring doppler shifts in neutral hydrogen (HI). Even Vera Rubin's optical measurements come from the emission lines in HII regions; while stars are associated with (and actually are responsible for heating) these regions, they are very young and have just been born from the gaseous (flat rotation-curve) structure.
Implications for Stellar-Dynamic Systems
I think that one key implication of the CK15 work is that old stellar-dynamical systems should not exhibit flat rotation curves. [This does not immediately contradict observations because it is extremely difficult to measure orbital velocities of individual stars; observers tend to be able to only measure mean velocity dispersions and "average" rotational velocities.] But, at the same time, the CK15 result should predict that the stars in these old stellar-dynamic systems should not be on circular orbits. They should be far from it! When a star is formed, it is injected into the galaxy with an initial velocity (magnitude and direction) that is identical to the velocity of the H-II region from which it formed; but it no longer feels the radial pressure gradient of the underlying gaseous disk, so its orbit cannot remain circular. It must develop a, perhaps considerable, radial component to its motion.
The farther you move away from the center of the galaxy, the larger the discrepancy will be between the orbital velocity of the gas (which is obeying a flat rotation curve) and the circular velocity that would be needed in order for a star (that feels no gas pressure) to stay in a circular orbit. Hence, stars that are formed progressively farther and farther out in a gaseous disk must develop progressively larger and larger radial velocity components. In the terms used by the stellar-dynamic community, such stellar-dynamic systems will be "hot" — because they have highly noncircular orbits — even though they still have very small vertical velocity components.
Prediction: Stellar disks that are "radially hot" but "vertically cold" when they form, cannot remain that way. Equipartition of energy demands that they will have to "puff up" — and, correspondingly shrink radially — to the extent where the kinetic energy in vertical motion is comparable to the kinetic energy in non-circular radial motion. I think that this can very naturally lead to an explanation for the entire Hubble sequence! For example: Late-type galaxies (those with small bulges and vertically-thin, gas-rich disks) will naturally evolve into stellar-dynamic (low amount of gas) systems that are quite thick; the time-scale of this evolution will be some combination of the star formation rate (gas disappearing) and the equipartition time-scale for stellar-dynamic systems. And how vertically thick the stellar disk becomes should reflect how extreme the mismatch was between the injection velocity when the star was born (from the flat-rotation-curve disk) and the required Keplerian circular velocity.
Related Work
I can't help but point out that one of my former graduate students — Eric Barnes, who is now on the faculty at UW-La Crosse — did dissertation research on a problem that relates to this. Remember the steady-state tumbling bars that John Cazes generated by following the nonlinear development of the bar-mode instability in initially axisymmetric polytropes? In Barnes & Tohline (2001), Eric pretended that this was a gaseous bar in a barred-spiral galaxy and asked, "If stars are born from this gas and injected into the underlying bar-like potential with the "circular" velocity of the gas, what elongated, stellar orbit will they traverse?
Additional remarks by J. E. Tohline
Date: 9 October 2015
A Potential Problem
After sleeping on this last night, I realized that there is a potential problem with this proposed explanation of flat rotation curves in galaxy disks. While C&K plan to eventually use an SCF code to generate full models of their new equilibrium disks with "flat" rotation curves, the current paper does not yet discuss the vertical structure of these disks. I am confident that they will find that their disks are pretty thick, vertically, and my recollection is that (HI) observations of edge-on spirals show that, in reality, the disks are vertically quite thin. The basic realization is that, anywhere the rotation curve deviates significantly from Keplerian, that means that (radially at least) there is considerable support from pressure gradients — as GK15 explain. But, since the pressure in gaseous configurations is isotropic, this means that in these regions of the disk, the vertical disk structure must also display a significant pressure support and, hence, be pretty thick. Maybe the (HI) disks are vertically thick in terms of volume density but, when integrated along the line of sight, the surface density projections make the disks look thin. At any rate, I think that the paper needs to address this question.
But wait! After a bit more thought, I'm remembering that the rotationally flattened isothermal configurations (with flat rotation curves) generated by Hayashi, Narita & Miyama (1982) can be thin as well as fat; it all depends on the ratio of the sound speed to the rotation velocity. So maybe there isn't a vertical thickness problem. Nevertheless this issue may need to be directly addressed in the paper.
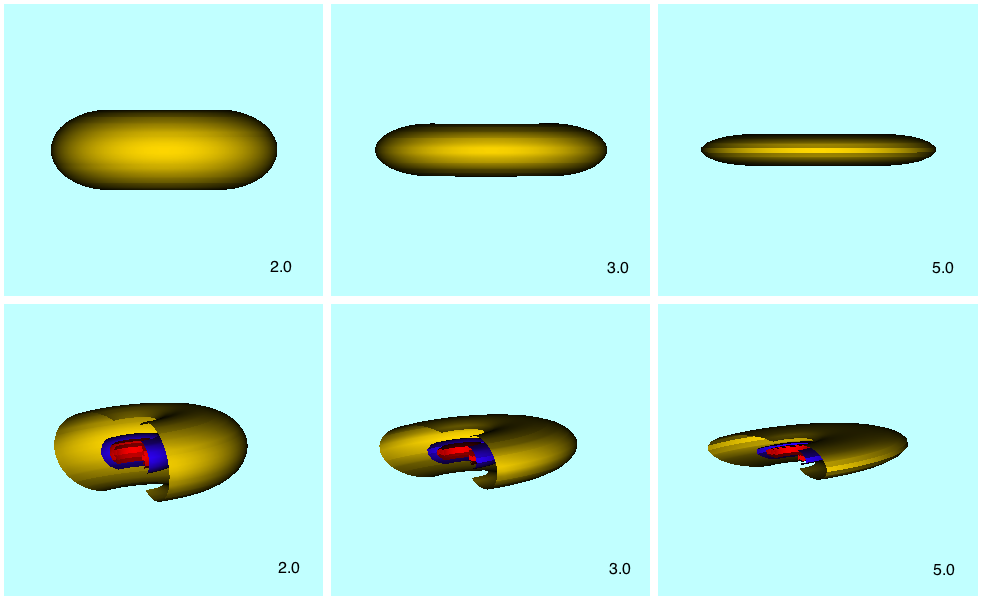
Just for fun, I decided to use the VisTrails rendering tool to display images of some of the analytically prescribed HNM82 disks. Three are shown in the following composite figure. Note that the HNM82 flattening parameter, <math>~\gamma</math>, has the following definition:
<math>\gamma = [1 + v_\varphi^2/(2c_s^2)] \, .</math>
In practice, for real galaxy disks, this flattening parameter must be much much larger than 5 (the largest value I've shown in the composite figure) because <math>~V_\varphi</math> is on the order of 100 km/s while the sound speed is less than or on the order of one km/s; hence even the simplistic HNM82 models would be very thin indeed!
| 3D Renderings of Isothermal Disks from Hayashi, Narita & Miyama (1982) |
|---|
| (Top) Edge-on view of three isothermal disks; (Bottom) Cut-away view of highest-density region of the same three disks. Values of flattening parameter, <math>~\gamma</math>, shown in bottom-right corner of each frame. |
Additional remarks by J. E. Tohline
Date: 11 December 2015
Looking Back Through My Research Files
Discovery
Yesterday, while cleaning out some of the file draws from my office at LSU, I stumbled upon a file folder dated 1987 with the label, "Analytic Model for Rotating Polytropes." This folder contained the following items:
- A hand-written derivation from Izumi Hachisu dated 26 May 1987 and titled, "Semi-analytic form of Rapidly Rotating Polytropes."
- Two (typed) rough drafts of a paper authored by J. E. Tohline, I. Hachisu, & D. M. Christodoulou and titled, "A General Analytic Model for Rotating Polytropes" — one draft dated 2 July 1987 and the other dated 15 July 1987.
- A manuscript authored by F. Schmitz (Institut für Astronomie und Astrophysik, der Universität Würzburg, Federal Republic of Germany) titled, "Equilibrium Structures of Differentially Rotating Self-gravitating Gases," and dated 17 July 1987.
- A two-page referee's report, written by Izumi Hachisu and typed on LSU letterhead, that evaluates the paper by F. Schmitz.
While I don't remember the entire story that underpins the contents of this file folder, I do remember discussing this research topic with Izumi and Dimitris. At that time we were quite familiar with the published work by Hayashi, Narita and Miyama (HNM82) which presents an analytic model for rotating isothermal gas clouds that have a constant-velocity rotation profile. We were wondering whether analytic models also could be determined for rotating gas clouds with a more general polytropic equation of state if a particular rotation profile was selected for each polytropic index. Evidently we dropped our pursuit of this problem when Izumi received the F. Schmitz manuscript to referee. Presumably this was because: (1) While we had formulated the problem mathematically, we had not discovered any closed-form solutions; and (2) by addressing a very similar problem in his manuscript, Schmitz had scooped us!
When I came across this file folder yesterday, I immediately thought about the CK15 manuscript and wondered to what extent there might be overlap between the CK15 work and this earlier work by F. Schmitz. I wondered, as well, what overlap there was between the CK15 work and the mathematical formulation of the problem as developed by Tohline, Hachisu, & Christodoulou over 25 years ago.
Examination of Overlap
We note, first, references to four separate papers by Schmitz can be found in the first paragraph of §4 in CK15.
CK15 present the following 2nd-order ODE to describe the equilibrium of rotating, polytropic configurations:
|
<math>~nc_o^2 \cdot \frac{1}{x}\frac{d}{dx} \biggl[ x\frac{d\tau^{1/n}}{dx} \biggr] + \tau</math> |
<math>~=</math> |
<math>~\frac{1}{x}\frac{dv^2}{dx} \, .</math> |
If we write the velocity profile as,
<math>v^2 = c_o^2 f(x) \, ,</math>
and switch <math>~\tau</math> to the more familiar, <math>~\theta^n</math>, the CK15 governing equation becomes,
|
<math>~nc_o^2 \cdot \frac{1}{x}\frac{d}{dx} \biggl[ x\frac{d\theta}{dx} \biggr] + \theta^n</math> |
<math>~=</math> |
<math>~\frac{c_o^2}{x}\frac{d}{dx}\biggl[ f(x) \biggr] </math> |
|
<math>~\Rightarrow ~~~~ c_o^2 \cdot \frac{1}{x}\frac{d}{dx} \biggl[ nx\frac{d\theta}{dx} -f(x)\biggr] + \theta^n</math> |
<math>~=</math> |
<math>~0 \, ,</math> |
which is the same as equation (10) of Tohline, Hachisu, & Christodoulou (1987), if you ignore variations in the vertical direction.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |