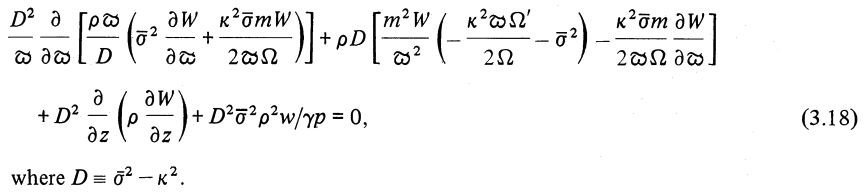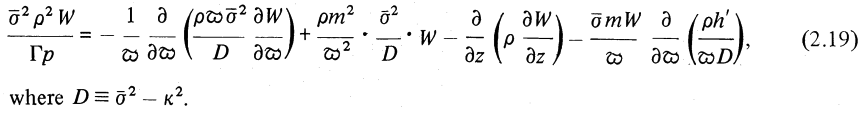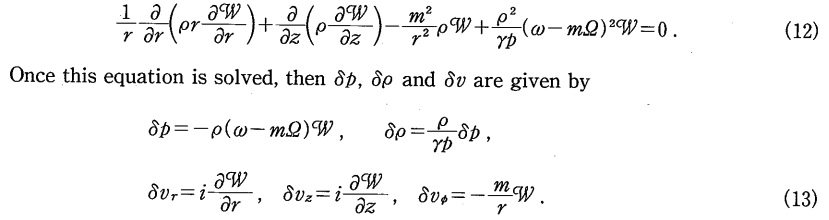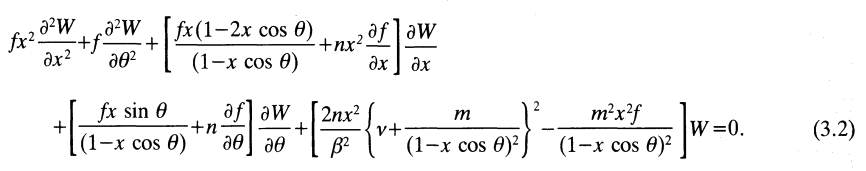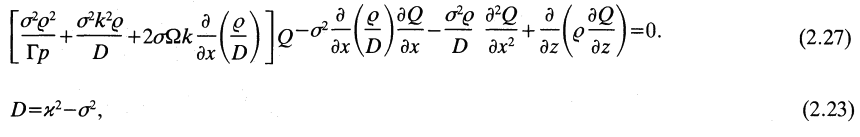User:Tohline/Apps/PapaloizouPringle84
Nonaxisymmetric Instability in Papaloizou-Pringle Tori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Linearized Principal Governing Equations in Cylindrical Coordinates
We begin by drawing from an accompanying derivation the relevant set of linearized principal governing equations, written in cylindrical coordinates but, following the lead of Papaloizou & Pringle (1984, MNRAS, 208, 721-750; hereafter, PP84), express each perturbation in the form,
|
<math>~q^'~~\rightarrow~~ q^' (\varpi,z) f_\sigma</math> |
where, |
<math>~f_\sigma \equiv e^{i(m\varphi + \sigma t)} \, ,</math> |
and, set <math>~\Phi^' = 0</math> — hence, the Poisson equation becomes irrelevant — because the torus is assumed not to be self-gravitating and the background (point source) potential, <math>~\Phi_0</math>, is assumed to be unchanging.
|
Set of Linearized Principal Governing Equations in Cylindrical Coordinates |
||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||
Next, taking derivatives of <math>~f_\sigma</math>, where indicated, then dividing every equation through by <math>~f_\sigma</math> gives,
| Linearized Adiabatic Form of the 1st Law of Thermodynamics | ||
|
<math>~\frac{P^' }{P_0}</math> |
<math>~=</math> |
<math>~ \frac{\gamma \rho^' }{\rho_0} \, ;</math> |
| Linearized <math>\varpi</math> Component of Euler Equation | ||
|
<math>~{\dot\varpi}^'[i(\sigma + m{\dot\varphi}_0)] - 2 {\dot\varphi}_0 (\varpi {\dot\varphi}^' ) </math> |
<math>~=</math> |
<math>~ - \frac{\partial}{\partial\varpi}\biggl( \frac{P^'}{\rho_0} \biggr) \, ; </math> |
| Linearized <math>\varphi</math> Component of Euler Equation | ||
|
<math>~(\varpi {\dot\varphi}^')[i(\sigma + m{\dot\varphi}_0)] + \frac{{\dot\varpi}^'}{\varpi}\biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] </math> |
<math>~=</math> |
<math>~- \frac{ im}{\varpi} \biggl(\frac{P^'}{\rho_0}\biggr) \, ; </math> |
| Linearized <math>~z</math> Component of Euler Equation | ||
|
<math>~ ~{\dot{z}}^'[i(\sigma + m{\dot\varphi}_0)] </math> |
<math>~=</math> |
<math>~ - \frac{\partial}{\partial z}\biggl( \frac{P^'}{\rho_0} \biggr) \, ; </math> |
| Linearized Continuity Equation | ||
|
<math>~\rho^'[i(\sigma + m{\dot\varphi}_0)] + i m\rho_0 {\dot\varphi}^' </math> |
<math>~=</math> |
<math>~ - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi {\dot\varpi}^' \biggr] - \frac{\partial}{\partial z} \biggl[ \rho_0 {\dot{z}}^' \biggr] \, . </math> |
These five equations match, respectively, equations (3.8) - (3.12) of PP84.
Rewritten Velocity Components
PP84
Again following the lead of PP84, we let <math>~W^'</math> represent the (normalized) perturbation in the fluid entropy, specifically,
|
<math>~W^' </math> |
<math>~\equiv</math> |
<math>~\frac{P^'}{\rho_0(\sigma + m{\dot\varphi}_0)} </math> |
|
<math>~\Rightarrow~~~~\frac{\partial}{\partial\varpi}\biggl(\frac{P^'}{\rho_0} \biggr)</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial\varpi} \biggl[ W^'(\sigma + m{\dot\varphi}_0 )\biggr]</math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0 )\frac{\partial W^'}{\partial\varpi} + mW^'\frac{\partial {\dot\varphi}_0 }{\partial\varpi} </math> |
in which case the three linearized components of the Euler equation may be rewritten as,
| Linearized <math>\varpi</math> Component of Euler Equation | ||
|
<math>~{\dot\varpi}^' </math> |
<math>~=</math> |
<math>~ i \biggl[ \frac{\partial W^'}{\partial\varpi} + \frac{mW^'}{(\sigma + m{\dot\varphi}_0)}\frac{\partial {\dot\varphi}_0 }{\partial\varpi} - \frac{2{\dot\varphi}_0 (\varpi {\dot\varphi}^' )}{(\sigma + m{\dot\varphi}_0)} \biggr] </math> |
| Linearized <math>\varphi</math> Component of Euler Equation | ||
|
<math>~(\varpi {\dot\varphi}^') </math> |
<math>~=</math> |
<math>~- \frac{ mW^'}{\varpi} + i~ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] \, ; </math> |
| Linearized <math>~z</math> Component of Euler Equation | ||
|
<math>~ ~{\dot{z}}^' </math> |
<math>~=</math> |
<math>~ i~\frac{\partial W^'}{\partial z} \, . </math> |
Using the second of these three relations to provide an expression for <math>~(\varpi {\dot\varphi}^')</math> in terms of <math>~W^'</math> and <math>~{\dot\varpi}^'</math>, and plugging this expression into the first relation allows us to solve for the radial component of the perturbed velocity in terms of <math>~W^'</math> and its radial derivative. Specifically, we obtain,
|
<math>~{\dot\varpi}^' </math> |
<math>~=</math> |
<math>~i \frac{\partial W^'}{\partial \varpi} + i~\frac{mW^'}{(\sigma + m{\dot\varphi}_0)} \biggl[ \frac{\kappa^2}{2\varpi {\dot\varphi}_0} - \frac{2 {\dot\varphi}_0 }{\varpi}\biggr] - i~ \frac{2 {\dot\varphi}_0 }{(\sigma + m{\dot\varphi}_0)} \biggl[ - \frac{ mW^'}{\varpi} + i~ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl( \frac{ \kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~i \frac{\partial W^'}{\partial \varpi} + i~\frac{mW^'}{(\sigma + m{\dot\varphi}_0)} \biggl[ \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr] + \biggl[ \frac{2 {\dot\varphi}_0 }{(\sigma + m{\dot\varphi}_0)} \biggr]\biggl[ \frac{{\dot\varpi}^'}{\varpi(\sigma + m{\dot\varphi}_0)}\biggl( \frac{ \kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~i \biggl[ \frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) \frac{ mW^'}{\bar\sigma} \biggr] + \biggl[ {\dot\varpi}^'\biggl( \frac{ \kappa^2 }{ {\bar\sigma}^2 } \biggr) \biggr] </math> |
|
<math>~\Rightarrow ~~~~ {\dot\varpi}^' ({\bar\sigma}^2 - \kappa^2 )</math> |
<math>~=</math> |
<math>~i \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) mW^' \bar\sigma \biggr] \, , </math> |
where, adopting notation from PP84,
|
<math>~\kappa^2 \equiv \frac{2{\dot\varphi}_0}{\varpi} \biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr]</math> |
and |
<math>~{\bar\sigma} \equiv (\sigma + m{\dot\varphi}_0) \, .</math> |
This means, as well, that,
|
<math>~(\varpi {\dot\varphi}^') ({\bar\sigma}^2 - \kappa^2 ) </math> |
<math>~=</math> |
<math>~- \frac{ mW^'}{\varpi} ({\bar\sigma}^2 - \kappa^2 ) - \frac{ 1 }{\varpi \bar\sigma }\biggl[ \frac{\kappa^2 \varpi }{ 2{\dot\varphi}_0 } \biggr] \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{2 {\dot\varphi}_0}{\varpi} + \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) mW^' \bar\sigma \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ m{\bar\sigma}^2 W^'}{\varpi} + \frac{ m\kappa^2W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{2 {\dot\varphi}_0}{\varpi} + \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \, . </math> |
In summary, the three components of the perturbed velocity are:
|
Cylindrical-Coordinate Components of the Perturbed Velocity from PP84 |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
where, the square of the epicyclic frequency,
| |||||||||||||||||||||
These three velocity-component expressions match, respectively, equations (3.14), (3.15), and (3.16) of PP84.
GGN86
In §2.2 of their paper, P. Goldreich, J. Goodman, and R. Narayan (1986, MNRAS, 221, 339) — hereafter, GGN86 — also present expressions for the three components of the perturbed velocity. Here we seek to identify key differences in approach but, ultimately, highlight the degree of agreement between the GGN86 and the PP84 analyses.
Preamble
First, let's make the substitution,
<math>Q_{JT} \equiv (\sigma + m{\dot\varphi}_0) W^' \, ,</math>
in which case,
|
<math>~\frac{\partial W^'}{\partial\varpi}</math> |
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)^{-1} \frac{\partial Q_{JT} }{\partial \varpi} - Q_{JT} (\sigma + m{\dot\varphi}_0)^{-2} m\frac{\partial {\dot\varphi}_0}{\partial \varpi} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)^{-2} \biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \, . </math> |
Then we can rewrite the radial component of the perturbed velocity as,
|
<math>~i~ {\dot\varpi}^' ( \kappa^2 - {\bar\sigma}^2 )</math> |
<math>~=</math> |
<math>~\biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) m Q_{JT} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} +m Q_{JT} \biggl[ \biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) -\biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} +m Q_{JT} \biggl\{ \frac{1}{\varpi^2} \biggl[ \frac{\partial (\varpi^2\dot\varphi_0)}{\partial\varpi} \biggr] -\biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~(\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi} + (2\dot\varphi_0)\frac{m Q_{JT}}{\varpi} </math> |
|
<math>~{\dot\varpi}^' ( \kappa^2 - {\bar\sigma}^2 )</math> |
<math>~=</math> |
<math>~- i~\bar\sigma \frac{\partial Q_{JT} }{\partial \varpi} - (2i\dot\varphi_0)\frac{m Q_{JT}}{\varpi} \, . </math> |
Similarly, we can rewrite the azimuthal component of the perturbed velocity as,
|
<math>~(\varpi {\dot\varphi}^') ( \kappa^2 - {\bar\sigma}^2) </math> |
<math>~=</math> |
<math>~ \frac{ m{\bar\sigma}^2 }{\varpi}(\sigma + m{\dot\varphi}_0)^{-1}Q_{JT} + \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl\{ ~(\sigma + m{\dot\varphi}_0)^{-2} \biggl[ (\sigma + m{\dot\varphi}_0)\frac{\partial Q_{JT} }{\partial \varpi}
- m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{m}{\bar\sigma } (\sigma + m{\dot\varphi}_0)^{-1}Q_{JT} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ m{\bar\sigma} }{\varpi} Q_{JT} + \frac{\kappa^2 }{ 2{\dot\varphi}_0 } \biggl\{ ~\biggl[ \frac{\partial Q_{JT} }{\partial \varpi}
- \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \frac{m}{\bar\sigma} Q_{JT} \biggr] +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{m}{\bar\sigma } Q_{JT} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\kappa^2 }{ 2{\dot\varphi}_0 } \biggr) \frac{\partial Q_{JT} }{\partial \varpi} + \bar\sigma \frac{mQ_{JT} }{\varpi} \, . </math> |
Finally, the vertical component of the perturbed velocity becomes,
|
<math>~ ~{\dot{z}}^' </math> |
<math>~=</math> |
<math>~ i~(\sigma + m{\dot\varphi}_0)^{-1} \frac{\partial Q_{JT}}{\partial z} \, . </math> |
|
<math>~\Rightarrow~~~~i~\bar\sigma {\dot{z}}^' </math> |
<math>~=</math> |
<math>~ -\frac{\partial Q_{JT}}{\partial z} \, . </math> |
Nod to Oort Constants and Simple Rotation Profiles
Acknowledging the galactic dynamics community's familiarity with the so-called Oort constants, and in anticipation of our review of the GGN86 derivation that follows, we define the following two "Oort functions":
|
<math>~A</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, ,</math> |
|
<math>~B</math> |
<math>~\equiv</math> |
<math>~\frac{1}{2}\biggl[ {\dot\varphi}_0 + \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, .</math> |
Given these definitions, we note that,
|
<math>~B - A </math> |
<math>~=</math> |
<math>~{\dot\varphi}_0 \, ;</math> |
and, given the definition of the square of the epicyclic frequency, above, we can write,
|
<math>~\kappa^2</math> |
<math>~=</math> |
<math>~4{\dot\varphi}_0 B = 4B (B - A) \, .</math> |
In line with our own discussion of simple rotation profiles (but note that, in that chapter, the variable we use for the power-law exponent is different from theirs), GGN86 adopt a generalized power-law rotation profile of the form (see their equation 2.1),
|
<math>~{\dot\varphi}_0(\varpi)</math> |
<math>~=</math> |
<math>~ \Omega_0 \biggl( \frac{\varpi}{\varpi_0} \biggr)^{-q} \, ,</math> |
in which case we also have,
|
<math>~\frac{\partial}{\partial \varpi} \biggl( \varpi {\dot\varphi}_0 \biggr)</math> |
<math>~=</math> |
<math>~ \frac{\partial}{\partial \varpi} \biggl[ \Omega_0 \varpi_0^{q} \varpi^{1-q}\biggr] = (1-q){\dot\varphi}_0 \, .</math> |
Given this particular adopted profile, it is therefore clear that,
|
<math>~A_\mathrm{GGN}</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - (1-q) {\dot\varphi}_0\biggr] = - \frac{q}{2} {\dot\varphi}_0 \, ;</math> |
|
<math>~B_\mathrm{GGN}</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{2}\biggl[ {\dot\varphi}_0 + (1-q) {\dot\varphi}_0\biggr] = \frac{1}{2} (2-q) {\dot\varphi}_0 \, ;</math> |
|
<math>~\kappa^2_\mathrm{GGN}</math> |
<math>~=</math> |
<math>~4{\dot\varphi}_0 \biggl[ \frac{1}{2} (2-q) {\dot\varphi}_0 \biggr] = 2(2-q){\dot\varphi}_0^2 \, .</math> |
These three expressions are in line with GGN86 equations (2.4), (2.6), and (2.24), respectively.
Velocity Components
Direct Comparison of Derived Equations
The left panel of the following equation-table presents, once again, our above rewrite of the three components of the perturbed velocity derived in PP84 after we have replaced <math>~\kappa^2</math> (on the right-hand side of the <math>~\varphi</math> component) with its expression in terms of the "Oort function", <math>~B</math>. For comparison, the right panel of the same equation-table shows the analogous perturbed velocity-component expressions derived by GGN86 (see their equations 2.21 - 2.25).
|
Rewrite of the Components of the Perturbed Velocity from PP84 |
Perturbed Velocity Components from §2.2 of GGN86 |
||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||
These sets of expressions are identical if we adopt the following three variable mappings,
|
<math>~Q_{JT}\equiv\bar\sigma W^'</math> |
<math>~\leftrightarrow</math> |
<math>~Q \, ,</math> |
|
<math>~-~\bar\sigma </math> |
<math>~\leftrightarrow</math> |
<math>~\sigma_\mathrm{GGN} \, ,</math> |
|
<math>~m/\varpi</math> |
<math>~\leftrightarrow</math> |
<math>~k \, ,</math> |
and recognize that the appropriate association between the variable names that has been used for the three perturbed velocity-components is:
|
<math>~{\dot\varpi}^'</math> |
<math>~\leftrightarrow</math> |
<math>~u \, ,</math> |
|
<math>~(\varpi {\dot\varphi}^') </math> |
<math>~\leftrightarrow</math> |
<math>~v \, ,</math> |
|
<math>~{\dot{z}}^'</math> |
<math>~\leftrightarrow</math> |
<math>~w \, .</math> |
Checking Self-Consistency
|
<math>~A</math> |
<math>~\equiv</math> |
<math>~- \frac{1}{2}\biggl[ {\dot\varphi}_0 - \frac{\partial}{\partial \varpi}\biggl( \varpi {\dot\varphi}_0 \biggr) \biggr] \, ,</math> |
|
<math>~\Rightarrow~~~~ -2A</math> |
<math>~=</math> |
<math>~- \varpi \frac{\partial {\dot\varphi}_0}{\partial \varpi}</math> |
|
<math>~\Rightarrow~~~~ \frac{\partial {\dot\varphi}_0}{\partial \varpi}</math> |
<math>~=</math> |
<math>~\frac{2A}{\varpi}</math> |
Now, expand the function, <math>~{\dot\varphi}_0(\varpi)</math> in a Taylor series …
|
<math>~{\dot\varphi}_0(\varpi) </math> |
<math>~\approx</math> |
<math>~\Omega_0 + (\varpi - \varpi_0)\frac{\partial {\dot\varphi}_0}{\partial\varpi}\biggr|_{\varpi_0}</math> |
|
|
<math>~=</math> |
<math>~\Omega_0 + (\varpi - \varpi_0)\frac{2A}{\varpi_0}</math> |
|
<math>~\Rightarrow ~~~~\bar\sigma \equiv (\sigma + m{\dot\varphi}_0)</math> |
<math>~\approx</math> |
<math>~\sigma + \biggl[m\Omega_0 + \frac{2mA}{\varpi_0}(\varpi - \varpi_0)\biggr]</math> |
Now, from equations (2.18) and (2.15) of GGN86, along with their definition of the independent variable, <math>~x</math>, we have,
|
<math>~- \sigma_\mathrm{GGN}</math> |
<math>~=</math> |
<math>~- \omega_\mathrm{GGN} + 2Akx</math> |
|
|
<math>~=</math> |
<math>~- \omega_\mathrm{GGN} + \frac{2mA}{\varpi_0} (\varpi-\varpi_0) \, .</math> |
Hence, we can understand the desired mapping, <math>\bar\sigma \leftrightarrow - \sigma_\mathrm{GGN}</math>, if we acknowledge the more fundamental mapping,
<math>~\omega_\mathrm{GGN} ~~ \leftrightarrow ~~ - (\sigma+m\Omega_0) \, .</math>
Adopting Kojima's (1986) <math>~y_1</math> and <math>~y_2</math> notation, which we have discussed in a separate but closely related chapter, we therefore have,
|
<math>~y_1 </math> |
<math>~=</math> |
<math>~\frac{\mathrm{Re}(\omega_\mathrm{GGN})}{\Omega_0} - m </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{1}{\Omega_0} \biggr) \mathrm{Re}\biggl[ - (\sigma+m\Omega_0) \biggr] - m </math> |
|
<math>~y_2 </math> |
<math>~=</math> |
<math>~\frac{\mathrm{Im}(\omega_\mathrm{GGN})}{\Omega_0} \, ,</math> |
Formulation of Eigenvalue Problem
In an effort to better understand the full three-dimensional structure of the eigenvector that characterizes nonaxisymmetric instabilities in Papaloizou-Pringle tori, we have studied in considerable depth five published analyses: The discovery paper, PP84, and papers by four separate groups that were published within a couple of years of the discovery paper — Papaloizou & Pringle (1985), Blaes (1985), Kojima (1986), and Goldreich, Goodman & Narayan (1986). In order to quantitatively compare and contrast the results of these separate analyses, it has been necessary to understand the terminology, technical approaches, and, in particular, the variable names adopted by each group. In order to accomplish this, here we show how the two-dimensional, 2nd-order PDE that fundamentally defines the PP-torus eigenvalue problem is derived in each case; in each of the four subsequently published papers, the derivation has its roots in the original PP84 derivation, as it should.
|
<math>~q(\varpi,\varphi,z,t) = q_0(\varpi,z) + q^'(\varpi,z)f_\sigma</math> |
||||
|
Source |
<math>~q^'</math> |
Eq. # |
Units |
<math>~f_\sigma</math> |
|---|---|---|---|---|
|
Here |
<math>~W^' \equiv \frac{P^'}{\rho_0(\sigma + m{\dot\varphi}_0)} </math> |
n/a |
specific
angular
momentum |
<math>~\exp[i(m\varphi + \sigma t)]</math> |
|
<math>~W \equiv p^'/[\rho(\sigma + m\Omega)]</math> |
(3.13) |
specific
angular
momentum |
||
|
<math>~W \equiv p^'/(\rho\bar\sigma)</math>
where, <math>~\bar\sigma\equiv \sigma + m\Omega</math> |
Near (2.12) |
specific
angular
momentum |
||
|
<math>~W \equiv \delta p/[\rho(\sigma + m\Omega)]</math> |
(1.5) |
specific
angular
momentum |
||
|
<math>~\mathcal{W} \equiv \delta p/[-\rho(\omega - m\Omega)]</math> |
(13) |
specific
angular
momentum |
||
|
<math>~Q = \rho^'(\Gamma p/\rho^2)</math> |
Near (2.25) |
enthalpy |
where, <math>~ky = \tfrac{m}{\varpi_0}(\varpi_0 \phi) = m\phi</math> |
|
|
<math>~Q \equiv \sigma_{GGN} \cdot W_{PP85}</math>
where, <math>~\sigma_{GGN} \equiv -{\bar\sigma}_{PP85}</math> (?) see above (?) |
Near (2.27) |
|||
The second column of the above table identifies, for example, the definition of the principal perturbation parameter, <math>~q^'</math>, that appears in our derivation as well as in the governing PDE of each of the five above-identified publications; we have purposely closely aligned our notation with the notation found in PP84. The third column of the table identifies the equation number within each paper where — or at least near where — the definition of this principal perturbation parameter can be found. The fourth column lists the physical units of the chosen principal perturbation parameter. It is fair to say that, in each case, the parameter was intended to be the ratio,<math>~P^'/\rho</math>, that is, the perturbed fluid enthalpy with units of velocity-squared, but PP84 found it mathematically "convenient" also to divide this quantity by a frequency that characterizes each unstable mode. Hence, the units of their principal perturbation parameter is "velocity-squared × time", which is also the units of specific angular momentum. Following the lead of PP84, three of the other four published analyses also adopted a principal perturbation parameter with units of specific angular momentum. Finally, the last column of the table identifies the specific expression that was adopted in each case for the factor, <math>~f_\sigma</math>, which facilitates a Fourier-analysis-based isolation of separate azimuthal eigenmodes. Note that the different adopted sign conventions for the mode eigenfrequency <math>~(\sigma</math> or <math>~\omega)</math> can introduce confusion when attempting to quantitatively compare different published derivations and eigenvector solutions.
While it is the case, as indicated in the above table, that Blaes (1985) begins his derivation (see his equation 3.1) using the same principal perturbation parameter, <math>~W</math>, as was introduced in PP84, by equation (3.2) he has shifted to a new dimensionless principal parameter — which he still calls <math>~W</math>, but which we will refer to as <math>~\delta W</math> (see below). We have deduced that this dimensionless perturbation parameter is defined as follows:
|
<math>~\delta W</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{\Omega_0 \rho_\mathrm{max}}{P_\mathrm{max}} \biggr]W^' </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(\sigma + m{\dot\varphi}_0)\rho_0}{\Omega_0 \rho_\mathrm{max}}\biggr]^{-1} \frac{P^'}{P_\mathrm{max}} \, .</math> |
Consistent with this, immediately after his equation (3.2), Blaes defines the dimensionless eigenfrequency,
|
<math>~\nu</math> |
<math>~\equiv</math> |
<math>~\frac{\sigma}{\Omega_0} \, .</math> |
Seminal Work by Papaloizou & Pringle
Let's plug the three expressions for the components of the perturbed velocity into the linearized continuity equation and, as well, replace <math>~\rho^'</math> in favor of <math>~W^'</math> via the expression,
|
<math>~W^' </math> |
<math>~\equiv</math> |
<math>~\frac{P^'}{\rho_0(\sigma + m{\dot\varphi}_0)} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{ (\sigma + m{\dot\varphi}_0)} \biggl(\frac{\gamma P_0 \rho^' }{\rho_0^2}\biggr) \, .</math> |
Also multiplying through by <math>~-i</math>, we obtain,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\rho^'[(\sigma + m{\dot\varphi}_0)] + \frac{m\rho_0}{\varpi} (\varpi {\dot\varphi}^' ) - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi (i {\dot\varpi}^' ) \biggr] - \frac{\partial}{\partial z} \biggl[ \rho_0 (i{\dot{z}}^') \biggr] </math> |
|
|
<math>~=</math> |
<math>~{\bar\sigma}^2 \biggl( \frac{\rho_0^2 W^'}{\gamma P_0 } \biggr) + \frac{m\rho_0}{\varpi ({\bar\sigma}^2 - \kappa^2 )} \biggl\{ - \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{({\bar\sigma}^2 - \kappa^2 )} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2}{2\varpi {\dot\varphi}_0} \biggr) mW^' \bar\sigma \biggr] \biggr\} + \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} \, . </math> |
Multiplying through by <math>~D^2 \equiv ({\bar\sigma}^2 - \kappa^2)^2</math> and reorganizing terms gives,
|
<math>~0 </math> |
<math>~=</math> |
<math>~ \frac{D^2}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{D} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr] \biggr\} + \frac{D m\rho_0}{\varpi} \biggl\{ - \frac{ m{\bar\sigma}^2 W^'}{\varpi} - \frac{\kappa^2 {\bar\sigma} }{ 2{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} +\biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \frac{mW^' }{\bar\sigma } \biggr] \biggr\} </math> |
|
|
|
<math>~ + D^2 \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} + \biggl( \frac{D^2 {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{D^2}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi}{D} \biggl[ {\bar\sigma}^2~\frac{\partial W^'}{\partial \varpi} +\biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr] \biggr\} + \rho_0 D \biggl\{ - \frac{m^2W^' }{\varpi^2 } \biggl[{\bar\sigma}^2 + \frac{\kappa^2 \varpi }{ 2 {\dot\varphi}_0 } \biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] - \frac{m\kappa^2 {\bar\sigma} }{ 2\varpi{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} \biggr]\biggr\} </math> |
|
|
|
<math>~ + D^2 \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} + \biggl( \frac{D^2 {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \biggr) \, . </math> |
As can be confirmed by comparing it to equation (3.18) of PP84 — which, to facilitate comparison, has been extracted and displayed in the following framed image — this expression matches the 2nd-order, two-dimensional PDE that defines the eigenvalue problem discussed by Papaloizou and Pringle in their seminal 1984 paper.
|
Equation (3.18) extracted without modification from p. 726 of Papaloizou & Pringle (1984)
"The dynamical stability of differentially rotating discs with constant specific angular momentum"
Monthly Notices of the Royal Astronomical Society, vol. 208, pp. 721-750 © Royal Astronomical Society |
After dividing through by <math>~D^2</math> and, again, rearranging terms, we also have,
|
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } </math> |
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{\frac{\rho_0 \varpi}{D} \biggl( \frac{\kappa^2mW^' \bar\sigma }{2\varpi {\dot\varphi}_0} \biggr) \biggr\} </math> |
|
|
|
<math>~ + \frac{\rho_0}{D} \biggl\{ \frac{m^2 {\bar\sigma}^2 W^' }{\varpi^2 } \biggr\} + \frac{\rho_0}{D} \biggl\{ \frac{m^2W^' }{\varpi^2 } \biggl[\frac{\kappa^2 \varpi }{ 2 {\dot\varphi}_0 } \biggl(\frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] \biggr\} + \frac{\rho_0}{D} \biggl\{\frac{m\kappa^2 {\bar\sigma} }{ 2\varpi{\dot\varphi}_0 } \biggl[ ~\frac{\partial W^'}{\partial \varpi} \biggr]\biggr\} </math> |
|
|
|
<math>~ - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} + \biggl\{ \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} \biggr\} - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
|
<math>~ -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0 \kappa^2m }{2 {\dot\varphi}_0 D} \biggl( W^' \bar\sigma \biggr) \biggr] + \frac{\rho_0 \kappa^2 m}{2 {\dot\varphi}_0 D} \biggl[ \frac{W^' }{\varpi} \cdot \frac{\partial (m{\dot\varphi}_0)}{\partial\varpi} \biggr] + \frac{\kappa^2 m \rho_0}{2{\dot\varphi}_0 D} \biggl[\frac{ {\bar\sigma} }{\varpi} \cdot \frac{\partial W^'}{\partial \varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr\} + \biggl\{ \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} \biggr\} - \frac{\partial}{\partial z} \biggl\{ \rho_0 \frac{\partial W^'}{\partial z} \biggr\} </math> |
|
|
|
<math>~ -\frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0 \kappa^2m }{2 {\dot\varphi}_0 D} ( W^' \bar\sigma ) \biggr] + \frac{\rho_0 \kappa^2 m}{2 {\dot\varphi}_0 D} \biggl[ \frac{1}{\varpi} \cdot \frac{\partial (W^' \bar\sigma)}{\partial\varpi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0 \varpi {\bar\sigma}^2}{D} \cdot \frac{\partial W^'}{\partial \varpi} \biggr) + \frac{\rho_0 m^2 {\bar\sigma}^2 W^' }{\varpi^2 D} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{m W^' \bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \, . </math> |
Here, it is advantageous to note that, in place of the definition of the (square of the) epicyclic frequency provided above, we could have equally well written,
<math>~\kappa^2 = \frac{1}{\varpi^3} \frac{d j_0^2}{d \varpi} \, ,</math>
where, <math>~j_0(\varpi)\equiv \varpi^2{\dot\varphi}_0(\varpi)</math> is a function that specifies how the fluid's specific angular momentum varies with radius in the initial, unperturbed, equilibrium configuration. (See our related discussion of Simple Rotation Profiles.) From this relation, we recognize as well that,
|
<math>~\frac{dj_0}{d\varpi}</math> |
<math>~=</math> |
<math>~\frac{\kappa^2 \varpi^3}{2j_0} = \frac{\kappa^2 \varpi}{2{\dot\varphi}_0} \, .</math> |
So the last term inside the square brackets of our expression could meaningfully be written as,
|
<math>~\biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr]</math> |
<math>~~\rightarrow~~</math> |
<math>~\biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{dj_0}{d\varpi} \biggr)\biggr] \, .</math> |
If we let <math>~h^'</math> represent the radial derivative of the specific angular momentum in the initial, unperturbed, equilibrium configuration (Papaloizou & Pringle use "h" instead of "j" to denote the specific angular momentum, and they use a prime to denote differentiation with respect to the radial coordinate), we see that our derived expression matches equation (2.19) of Papaloizou & Pringle (1985) — which, to facilitate comparison, has been extracted and displayed in the following framed image. Clearly this mathematical definition of the eigenvalue problem discussed by PP85 is fundamentally the same as the one introduced and discussed in PP84.
|
Equation (2.19) extracted without modification from p. 803 of Papaloizou & Pringle (1985)
"The dynamical stability of differentially rotating discs. II"
Monthly Notices of the Royal Astronomical Society, vol. 213, pp. 799-820 © Royal Astronomical Society |
Analyses of Configurations with Uniform Specific Angular Momentum
Kojima's Setup
Presumably PP85 rewrote the equation in the latest form presented above in order to help make it clear how the equation simplifies (specifically, the last term on the right-hand side vanishes) for configurations that initially have uniform specific angular momentum — that is, for configurations in which <math>~h^' = 0</math>. But other simplifications arise as well because the epicyclic frequency, <math>~\kappa</math>, also goes to zero in configurations with uniform specific angular momentum. This means that the frequency ratio, <math>~{\bar\sigma}^2/D</math>, that appears in two terms of our derived expression goes to unity, that is,
|
<math>~\frac{{\bar\sigma}^2}{D}\biggr|_{j_0-\mathrm{constant}} = \biggl[ \frac{{\bar\sigma}^2}{{\bar\sigma}^2 - \kappa^2}\biggr]_{j_0-\mathrm{constant}}</math> |
<math>~~\rightarrow~~</math> |
<math>~1 \, .</math> |
Implementing both of these simplifications, the latest form of our "eigenvalue problem" equation becomes,
|
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } </math> |
<math>~=</math> |
<math>~- \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \cancelto{1}{\biggl(\frac{{\bar\sigma}^2}{D} \biggr)} \rho_0 \varpi \cdot \frac{\partial W^'}{\partial \varpi} \biggr] + \cancelto{1}{\biggl(\frac{{\bar\sigma}^2}{D} \biggr)} \frac{\rho_0 m^2 W^' }{\varpi^2} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{m W^' \bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \cancelto{0}{\biggl( \frac{dj_0 }{d\varpi } \biggr)} \biggr] </math> |
|
<math>~\Rightarrow~~~~0 </math> |
<math>~=</math> |
<math>~ \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi \cdot \frac{\partial W^'}{\partial \varpi} \biggr] + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W^'}{\partial z} \biggr) - \frac{\rho_0 m^2 W^' }{\varpi^2} + \frac{ {\bar\sigma}^2 \rho_0^2 W^'}{\gamma P_0 } \, . </math> |
As can be confirmed by comparing it to equation (12) of Kojima (1986) — which, to facilitate comparison, has been extracted and displayed in the following framed image — this expression matches the 2nd-order, two-dimensional PDE that defines the eigenvalue problem discussed by Kojima.
|
Equations (12) & (13) extracted without modification from p. 254 of Kojima (1986)
"The Dynamical Stability of a Fat Disk with Constant Specific Angular Momentum"
Progress of Theoretical Physics, vol. 75, pp. 251-261 © The Physical Society of Japan |
This expression also serves as the starting point for the stability analysis presented by Blaes (1985) — see his equation (3.1), but note that he has replaced the adiabatic exponent with the polytropic index via the relation, <math>~\gamma = (n+1)/n</math>.
Equivalent Dimensionless Expression
Now, as should be clear from our introductory description of barotropic structures, because the initial, unperturbed Papaloizou-Pringle torus is a polytropic configuration, the functions <math>~P_0(\varpi,z)</math> and <math>~\rho_0(\varpi,z)</math> can both be expressed in terms of the dimensionless enthalpy distribution,
|
<math>~\Theta_H(\varpi,z) </math> |
<math>~=</math> |
<math>~1 - \frac{1}{\beta^2}\biggl[ \chi^{-2} - 2 ( \chi^2 + \zeta^2 )^{-1/2} + 1 \biggr] \, ,</math> |
where,
|
<math>~\chi \equiv \frac{\varpi}{\varpi_0} \, ,</math> <math>~\zeta \equiv \frac{z}{\varpi_0} \, ,</math> <math>~\beta^2 \equiv \frac{2n}{\mathfrak{M}_0^2} \, ,</math> |
<math>~</math> |
<math>~</math> |
and <math>~\mathfrak{M}_0</math> is the Mach number of the circular, azimuthal flow at the pressure and density maximum. Specifically (see also equation 1.1 of Blaes85),
<math>~P_0 = P_\mathrm{max} \Theta_H^{n+1} </math> and <math>~\rho_0 = \rho_\mathrm{max} \Theta_H^{n} \, .</math>
Making these state-variable substitutions in the PDE that we have just presented for comparison with Kojima's work, we have,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~ \frac{\rho_\mathrm{max}}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \Theta_H^n \varpi \cdot \frac{\partial W^'}{\partial \varpi} \biggr] + \rho_\mathrm{max}\frac{\partial}{\partial z} \biggl(\Theta_H^n \frac{\partial W^'}{\partial z} \biggr) + \rho_\mathrm{max}\biggl\{ \frac{ n{\bar\sigma}^2 \Theta_H^{(n-1)} \rho_\mathrm{max} }{(n+1) P_\mathrm{max} } - \frac{\Theta_H^n m^2 }{\varpi^2} \biggr\} W^' \, . </math> |
In an effort to make this entire expression dimensionless, let's define a dimensionless enthalpy perturbation via the relation,
|
<math>~\delta W</math> |
<math>~\equiv \biggl[ \frac{\Omega_0 \rho_\mathrm{max}}{P_\mathrm{max}} \biggr]W^' \, ,</math> |
<math>~</math> |
and multiply our expression through by <math>~(\varpi_0^2 \Omega_0/P_\mathrm{max})</math>. This gives,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~ \frac{1}{\chi} \frac{\partial}{\partial\chi} \biggl[ \Theta_H^n \chi \cdot \frac{\partial (\delta W) }{\partial \chi} \biggr] + \frac{\partial}{\partial \zeta} \biggl[ \Theta_H^n \frac{\partial (\delta W) }{\partial \zeta} \biggr] + \biggl[ \Theta_H^{n-1} \biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 \frac{ n\Omega_0^2 \rho_\mathrm{max} \varpi_0^2}{(n+1)P_\mathrm{max} }- \frac{\Theta_H^n m^2 }{\chi^2} \biggr]\delta W </math> |
|
|
<math>~=</math> |
<math>~ \Theta_H^n \cdot \frac{\partial^2 (\delta W) }{\partial \chi^2} +\Theta_H^n \cdot \frac{\partial^2 (\delta W) }{\partial \zeta^2} + \biggl[ \Theta_H^{n-1} \biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 \frac{2n}{\beta^2} - \frac{\Theta_H^n m^2 }{\chi^2} \biggr]\delta W </math> |
|
|
|
<math>~ +\frac{1}{\chi} \frac{\partial (\delta W) }{\partial \chi} \biggl[\Theta_H^n + n\chi \Theta_H^{n-1} \frac{\partial \Theta_H}{\partial\chi} \biggr] + n \Theta_H^{n-1} ~\frac{\partial (\delta W) }{\partial \zeta} \frac{\partial \Theta_H}{\partial \zeta} </math> |
|
|
<math>~=</math> |
<math>~\Theta_H^{n-1} \biggl\{ \Theta_H \cdot \frac{\partial^2 (\delta W) }{\partial \chi^2} +\Theta_H \cdot \frac{\partial^2 (\delta W) }{\partial \zeta^2} + \biggl[\frac{\Theta_H}{ \chi } + n \frac{\partial \Theta_H}{\partial\chi} \biggr]\frac{\partial (\delta W) }{\partial \chi} </math> |
|
|
|
<math>~ + \biggl[ n \frac{\partial \Theta_H}{\partial \zeta} \biggr] \frac{\partial (\delta W) }{\partial \zeta} + \biggl[ \frac{2n }{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 \Theta_H}{\chi^2} \biggr]\delta W \biggr\} \, . </math> |
[It appears as though I'm on the right track because this expression is very similar to equation (3.2) of Blaes85!]
Change to Off-Axis Polar-Coordinate System
In his effort to derive an analytic solution to this eigenvalue problem, Blaes (1985) adopted a different meridional-plane coordinate system. As is illustrated in his Figure 1, Blaes shifted from the (dimensionless) rectilinear <math>~(\chi,\zeta)</math> system to a (dimensionless) polar-coordinate <math>~(x,\theta)</math> system whose origin sits at the pressure-maximum of the initial, unperturbed Papaloizou-Pringle torus. Mapping between these two coordinate systems is accomplished via the relations (see equation 2.1 of Blaes85),
|
<math>~x^2 = (1-\chi)^2 + \zeta^2</math> |
and |
<math>~\theta = \tan^{-1}\biggl[\frac{\zeta}{1-\chi}\biggr] \, ;</math> |
| or | ||
|
<math>~\chi = 1 - x\cos\theta</math> |
and |
<math>~\zeta = x\sin\theta \, .</math> |
Mapping of partial derivatives is accomplished via the relations,
|
<math>~\frac{\partial}{\partial\chi}</math> |
<math>~\rightarrow</math> |
<math>~ - \cos\theta \cdot \frac{\partial}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial}{\partial\theta} \, , </math> |
|
<math>~\frac{\partial}{\partial\zeta}</math> |
<math>~\rightarrow</math> |
<math>~ \sin\theta \cdot \frac{\partial}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial}{\partial\theta} \, . </math> |
This means, for example, that,
|
<math>~\frac{\partial^2(\delta W)}{\partial \chi^2}</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial\chi}\biggl[ - \cos\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ -\cos\theta \cdot\frac{\partial}{\partial x}\biggl[ - \cos\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr] + \frac{\sin\theta}{x} \cdot \frac{\partial}{\partial\theta}\biggl[ - \cos\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -\cos\theta \biggl[ - \cos\theta \cdot \frac{\partial^2(\delta W)}{\partial x^2} -\frac{\sin\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{\sin\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial x ~\partial\theta} \biggr] </math> |
|
|
|
<math>~ + \frac{\sin\theta}{x} \biggl[ \sin\theta \cdot \frac{\partial(\delta W)}{\partial x} - \cos\theta \cdot \frac{\partial^2(\delta W)}{\partial\theta~\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{\sin\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \cos^2\theta \cdot \frac{\partial^2(\delta W)}{\partial x^2} +\frac{\sin\theta\cos\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} -\frac{\sin\theta\cos\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial x ~\partial\theta} \biggr] </math> |
|
|
|
<math>~ +\biggl[ \frac{\sin^2\theta}{x} \cdot \frac{\partial(\delta W)}{\partial x} - \frac{\sin\theta\cos\theta}{x} \cdot \frac{\partial^2(\delta W)}{\partial\theta~\partial x} +\frac{\sin\theta\cos\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{\sin^2\theta}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \cos^2\theta \cdot \frac{\partial^2(\delta W)}{\partial x^2} +\frac{\sin^2\theta}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \frac{\sin^2\theta}{x} \cdot \frac{\partial(\delta W)}{\partial x} +\frac{2\sin\theta\cos\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} -\frac{2\sin\theta\cos\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial x ~\partial\theta} \, . </math> |
Also,
|
<math>~\frac{\partial^2(\delta W)}{\partial \zeta^2}</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial\zeta}\biggl[ \sin\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \sin\theta \cdot \frac{\partial}{\partial x}\biggl[ \sin\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr] + \frac{\cos\theta}{x} \cdot \frac{\partial}{\partial\theta}\biggl[ \sin\theta \cdot \frac{\partial(\delta W)}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \sin\theta \biggl[ \sin\theta \cdot \frac{\partial^2(\delta W)}{\partial x^2} -\frac{\cos\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{\cos\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial x ~\partial\theta} \biggr] </math> |
|
|
|
<math>~ +\frac{\cos\theta}{x} \biggl[ \cos\theta \cdot \frac{\partial(\delta W)}{\partial x} +\sin\theta \cdot \frac{\partial^2(\delta W)}{\partial\theta~\partial x} -\frac{\sin\theta}{x}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{\cos\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \sin^2\theta \cdot \frac{\partial^2(\delta W)}{\partial x^2} +\frac{\cos^2\theta}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} +\frac{\cos^2\theta}{x} \cdot \frac{\partial(\delta W)}{\partial x} -\frac{2\sin\theta \cos\theta}{x^2}\cdot \frac{\partial(\delta W)}{\partial\theta} +\frac{2\sin\theta \cos\theta}{x}\cdot \frac{\partial^2(\delta W)}{\partial x ~\partial\theta} \, . </math> |
A significant amount of simplification occurs when these two expressions are added. Specifically, we have,
|
<math>~ \frac{\partial^2(\delta W)}{\partial \chi^2} +\frac{\partial^2(\delta W)}{\partial \zeta^2} </math> |
<math>~=</math> |
<math>~ \frac{\partial^2(\delta W)}{\partial x^2} +\frac{1}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} +\frac{1}{x} \cdot \frac{\partial(\delta W)}{\partial x} \, . </math> |
With this as a start, a coordinate mapping of our above-derived dimensionless "eigenvalue problem" expression gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \Theta_H \biggl[ \frac{\partial^2 (\delta W) }{\partial \chi^2} + \frac{\partial^2 (\delta W) }{\partial \zeta^2} \biggr] + \biggl[ \frac{2n }{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 \Theta_H}{\chi^2} \biggr]\delta W </math> |
|
|
|
<math>~ + \biggl[\frac{\Theta_H}{ \chi } + n \frac{\partial \Theta_H}{\partial\chi} \biggr]\frac{\partial (\delta W) }{\partial \chi} + \biggl[ n \frac{\partial \Theta_H}{\partial \zeta} \biggr] \frac{\partial (\delta W) }{\partial \zeta} </math> |
|
|
<math>~=</math> |
<math>~ \Theta_H \biggl[ \frac{\partial^2(\delta W)}{\partial x^2} +\frac{1}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} +\frac{1}{x} \cdot \frac{\partial(\delta W)}{\partial x} \biggr] + \biggl[ \frac{2n }{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 \Theta_H}{(1-x\cos\theta)^2} \biggr]\delta W </math> |
|
|
|
<math>~ + \biggl\{\frac{\Theta_H}{ \chi } + n \biggl[ - \cos\theta \cdot \frac{\partial\Theta_H}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr]\biggr\} \biggl[- \cos\theta \cdot \frac{\partial (\delta W)}{\partial x} +\frac{\sin\theta}{x}\cdot \frac{\partial (\delta W)}{\partial\theta} \biggr] </math> |
|
|
|
<math>~ + n\biggl[ \sin\theta \cdot \frac{\partial\Theta_H}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial\Theta_H}{\partial\theta} \biggr] \biggl[ \sin\theta \cdot \frac{\partial (\delta W)}{\partial x} +\frac{\cos\theta}{x}\cdot \frac{\partial (\delta W)}{\partial\theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \Theta_H \biggl[ \frac{\partial^2(\delta W)}{\partial x^2} +\frac{1}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2} +\frac{1}{x} \cdot \frac{\partial(\delta W)}{\partial x} \biggr] + \biggl[ \frac{2n }{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 \Theta_H}{(1-x\cos\theta)^2} \biggr]\delta W </math> |
|
|
|
<math>~ + \biggl\{- \frac{\cos\theta\cdot\Theta_H}{ (1-x\cos\theta)} + n \biggl[ \cos^2\theta \cdot \frac{\partial\Theta_H}{\partial x} -\frac{\sin\theta \cos\theta}{x}\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr]\biggr\} \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + n\biggl[ \sin^2\theta \cdot \frac{\partial\Theta_H}{\partial x} +\frac{\sin\theta\cos\theta}{x}\cdot \frac{\partial\Theta_H}{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + \biggl\{\frac{\sin\theta\cdot\Theta_H}{ x(1-x\cos\theta) } + n \biggl[ - \frac{\sin\theta\cos\theta}{x} \cdot \frac{\partial\Theta_H}{\partial x} +\frac{\sin^2\theta}{x^2}\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr]\biggr\} \cdot \frac{\partial (\delta W)}{\partial\theta} </math> |
|
|
|
<math>~ + n\biggl[ \frac{\sin\theta\cos\theta}{x} \cdot \frac{\partial\Theta_H}{\partial x} +\frac{\cos^2\theta}{x^2}\cdot \frac{\partial\Theta_H}{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} </math> |
|
|
<math>~=</math> |
<math>~ \Theta_H \biggl[ \frac{\partial^2(\delta W)}{\partial x^2} +\frac{1}{x^2}\cdot \frac{\partial^2(\delta W)}{\partial\theta^2}\biggr] + \biggl[ \frac{2n }{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 \Theta_H}{(1-x\cos\theta)^2} \biggr]\delta W </math> |
|
|
|
<math>~ + \biggl\{\frac{\Theta_H}{x}- \frac{\cos\theta\cdot\Theta_H}{ (1-x\cos\theta)} + n \biggl[ \frac{\partial\Theta_H}{\partial x} \biggr]\biggr\} \cdot \frac{\partial (\delta W)}{\partial x} + \biggl[\frac{\sin\theta\cdot\Theta_H}{ x(1-x\cos\theta) } + \frac{n}{x^2}\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} \, . </math> |
Finally, after multiplying through by <math>~x^2</math> and rearranging terms, we obtain,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \Theta_H x^2\cdot \frac{\partial^2(\delta W)}{\partial x^2} +\Theta_H \cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \biggl\{\Theta_H x \biggl[\frac{1-2x \cos\theta}{ 1-x\cos\theta}\biggr] + nx^2 \cdot \frac{\partial\Theta_H}{\partial x} \biggr\} \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + \biggl[\frac{\Theta_Hx\sin\theta}{ (1-x\cos\theta) } + n\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} + \biggl[ \frac{2n x^2}{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 x^2\Theta_H}{(1-x\cos\theta)^2} \biggr]\delta W \, . </math> |
Note that, because Blaes (1985) is only considering tori with a uniform specific angular momentum distribution, <math>~q=2</math>, the frequency ratio, <math>~(\bar\sigma/\Omega_0)</math>, may be rewritten as,
|
<math>~\frac{\bar\sigma}{\Omega_0}</math> |
<math>~=</math> |
<math>~\frac{\sigma + m{\dot\varphi}_0(\varpi)}{\Omega_0} = \frac{\sigma}{\Omega_0} + m\chi^{-q} = \frac{\sigma}{\Omega_0} + \frac{m}{(1-x\cos\theta)^2} \, .</math> |
As can be confirmed by comparing it to equation (3.2) of Blaes (1985) — which, to facilitate comparison, has been extracted and displayed in the following framed image — our just-derived PDE matches the 2nd-order, two-dimensional PDE that defines the dimensionless eigenvalue problem discussed by Blaes (1985).
|
Equation (3.2) extracted without modification from p. 558 of O. M. Blaes (1985)
"Oscillations of Slender Tori"
Monthly Notices of the Royal Astronomical Society, vol. 216, Issue 3, October 1985, pp. 553-563 |
|
This digital image has been posted by permission of author, O.M. Blaes (via email dated 19 July 2020), and by permission of Oxford University Press on behalf of the Royal Astronomical Society (via email dated 31 July 2020). Original publication website: https://academic.oup.com/mnras/article/216/3/553/1005987
|
Isolating on the right-hand side terms that explicitly involve the dimensionless eigenfrequency, <math>~\nu \equiv (\sigma/\Omega_0)</math>, this governing PDE may also be written in the form (see equations 4.1 and 4.2 of Blaes85),
|
<math>~\hat{L} (\delta W)</math> |
<math>~=</math> |
<math>~-2n(1-\Theta_H)(M\nu^2 + N\nu)(\delta W) \, ,</math> |
where,
|
<math>~\hat{L} (\delta W)</math> |
<math>~\equiv</math> |
<math>~ \Theta_H x^2\cdot \frac{\partial^2(\delta W)}{\partial x^2} +\Theta_H \cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \biggl\{\Theta_H x \biggl[\frac{1-2x \cos\theta}{ 1-x\cos\theta}\biggr] + nx^2 \cdot \frac{\partial\Theta_H}{\partial x} \biggr\} \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + \biggl[\frac{\Theta_Hx\sin\theta}{ (1-x\cos\theta) } + n\cdot \frac{\partial \Theta_H}{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} + \biggl[ \frac{2n x^2 m^2}{\beta^2(1-x\cos\theta)^4} - \frac{m^2 x^2\Theta_H}{(1-x\cos\theta)^2} \biggr]\delta W \, , </math> |
|
<math>~M</math> |
<math>~\equiv</math> |
<math>~\frac{x^2}{(1-\Theta_H)\beta^2} \, ,</math> |
|
<math>~N</math> |
<math>~\equiv</math> |
<math>~\frac{2mx^2}{(1-\Theta_H)\beta^2(1-x\cos\theta)^2} \, .</math> |
Introduce Coordinate-Parameter η
Following the lead of Blaes (1985), and without loss of generality, we can everywhere replace the dimensionless function representing the unperturbed equilibrium enthalpy distribution, <math>~\Theta_H</math> — that varies from unity at the cross-sectional center of the torus to zero at the torus surface — with the parameter,
|
<math>~\eta^2</math> |
<math>~\equiv</math> |
<math>~1 - \Theta_H \, ,</math> |
that varies from zero at the (cross-sectional) center to unity at the surface. Making this substitution, our governing PDE becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1-\eta^2) x^2\cdot \frac{\partial^2(\delta W)}{\partial x^2} +(1-\eta^2) \cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \biggl\{(1-\eta^2) x \biggl[\frac{1-2x \cos\theta}{ 1-x\cos\theta}\biggr] + nx^2 \cdot \frac{\partial(1-\eta^2) }{\partial x} \biggr\} \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + \biggl[\frac{(1-\eta^2) x\sin\theta}{ (1-x\cos\theta) } + n\cdot \frac{\partial (1-\eta^2) }{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} + \biggl[ \frac{2n x^2}{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 x^2(1-\eta^2) }{(1-x\cos\theta)^2} \biggr]\delta W </math> |
|
|
<math>~=</math> |
<math>~ x^2 (1-\eta^2)\cdot \frac{\partial^2(\delta W)}{\partial x^2} + (1-\eta^2) \cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \biggl\{x (1-\eta^2) \biggl[\frac{1-2x \cos\theta}{ 1-x\cos\theta}\biggr] -2 nx^2 \eta \cdot \frac{\partial \eta }{\partial x} \biggr\} \cdot \frac{\partial (\delta W)}{\partial x} </math> |
|
|
|
<math>~ + \biggl[\frac{(1-\eta^2) x\sin\theta}{ (1-x\cos\theta) } -2n\eta \cdot \frac{\partial \eta }{\partial\theta} \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} + \biggl[ \frac{2n x^2}{\beta^2}\biggl( \fracTemplate:\bar\sigma{\Omega_0} \biggr)^2 - \frac{m^2 x^2(1-\eta^2) }{(1-x\cos\theta)^2} \biggr]\delta W \, . </math> |
Slender Torus Approximation
Blaes85
Generally, in Papaloizou-Pringle tori, the equilibrium enthalpy distribution is a function of both <math>~x</math> and <math>~\theta</math>, hence also, <math>~\eta = \eta(x,\theta)</math>. However, as Blaes (1985) explains — see the discussion associated with his equation (2.6) — to lowest order in <math>~x</math>,
<math>~\eta \approx \frac{x}{\beta} \, ,</math>
and the function <math>~\eta</math> has no dependence on <math>~\theta</math>. Hence, near the (cross-sectional) center of each torus, we can make the substitutions,
<math>\frac{\partial \eta}{\partial \theta} = 0 \, ,</math> and <math>~x = \beta\eta </math> <math>~\Rightarrow</math> <math>\frac{\partial}{\partial x} = \frac{1}{\beta}\cdot\frac{\partial}{\partial \eta} \, ,</math>
and our latest PDE expression becomes,
|
<math>~0</math> |
<math>~\approx</math> |
<math>~ \eta^2 (1-\eta^2)\cdot \frac{\partial^2(\delta W)}{\partial \eta^2} + (1-\eta^2) \cdot \frac{\partial^2(\delta W)}{\partial\theta^2} + \biggl\{\eta (1-\eta^2) \biggl[\frac{1-2\beta\eta \cos\theta}{ 1-\beta\eta\cos\theta}\biggr] -2 n \eta^3 \biggr\} \cdot \frac{\partial (\delta W)}{\partial \eta} </math> |
|
|
|
<math>~ + \biggl[\beta\eta\frac{(1-\eta^2)\sin\theta}{ (1-\beta\eta\cos\theta) } \biggr] \cdot \frac{\partial (\delta W)}{\partial\theta} + \biggl\{ 2n\eta^2 \biggl[ \frac{\sigma}{\Omega_0} + \frac{m}{(1-\beta\eta\cos\theta)^2} \biggr]^2 - \frac{m^2 \beta^2 \eta^2(1-\eta^2) }{(1-\beta\eta\cos\theta)^2} \biggr\}\delta W \, . </math> |
Finally, the slim-torus approximation results from setting <math>~\beta = 0</math>, in which case the eigenvalue problem is defined by the expression,
|
<math>~0</math> |
<math>~\approx</math> |
<math>~ \eta^2 (1-\eta^2)\cdot \frac{\partial^2(\delta W)^{(0)}}{\partial \eta^2} + (1-\eta^2) \cdot \frac{\partial^2(\delta W)^{(0)}}{\partial\theta^2} + \biggl[ \eta (1-\eta^2) -2 n \eta^3 \biggr] \cdot \frac{\partial (\delta W)^{(0)}}{\partial \eta} + 2n\eta^2 \biggl( \frac{\sigma}{\Omega_0} + m \biggr)^2 (\delta W)^{(0)} \, , </math> |
where, quoting Blaes (1985), "the superscript (0) denotes the infinitely slender limit." As can be confirmed by comparing it to equation (1.6) of Blaes (1985) — which, to facilitate comparison, has been extracted and displayed in the following framed image — our just-derived PDE matches the 2nd-order, two-dimensional PDE that defines the dimensionless eigenvalue problem in the slender torus approximation.
|
Equation (1.6) — identical to Eq. (3.5) — extracted without modification from p. 555 of O. M. Blaes (1985)
"Oscillations of Slender Tori"
Monthly Notices of the Royal Astronomical Society, vol. 216, Issue 3, October 1985, pp. 553-563 |
|
This digital image has been posted by permission of author, O.M. Blaes (via email dated 19 July 2020), and by permission of Oxford University Press on behalf of the Royal Astronomical Society (via email dated 31 July 2020). Original publication website: https://academic.oup.com/mnras/article/216/3/553/1005987
|
In a separate chapter, we dissect the Blaes85 assertion that Jacobi Polynomials provide an analytic eigenvector solution to this specific "slim torus" eigenvalue problem.
GGN86
The discussion in this subsection builds on our above derivation of equation (3.18) in PP84 and equation (2.19) in PP85. Following along the lines of the variable substitution that was made earlier in our "preamble", let's replace <math>~W^'</math> with <math>~Q_{JT} \equiv \bar\sigma W^'</math> throughout this expression. As was also pointed out above, because <math>~\bar\sigma</math> is a function of the radial coordinate, we note that,
|
<math>~\frac{\partial \bar\sigma}{\partial\varpi}</math> |
<math>~=</math> |
<math>~ m \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \, , </math> |
and,
|
<math>~\frac{\partial W^'}{\partial\varpi}</math> |
<math>~=</math> |
<math>~{\bar\sigma}^{-2} \biggl[ {\bar\sigma} \frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \, . </math> |
Making these substitutions in equation (2.19) of PP85, we have,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~ \frac{ {\bar\sigma}^2 \rho_0^2 Q_{JT} }{\gamma P_0 \bar\sigma } + \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi }{D} \cdot \biggl[ {\bar\sigma} \frac{\partial Q_{JT} }{\partial \varpi} - m Q_{JT} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr]\biggr\} - \frac{\rho_0 m^2 {\bar\sigma} Q_{JT} }{\varpi^2 D} + \frac{1}{\bar\sigma}\frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) + \frac{m Q_{JT} }{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{\varpi D} \biggl( \frac{\varpi \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \, . </math> |
Then, multiplying through by <math>~\bar\sigma</math> and rearranging terms, gives,
|
<math>~ 0 </math> |
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggl( \frac{ \kappa^2 }{2 {\dot\varphi}_0 } \biggr)\biggr] \biggr\}Q_{JT} ~ + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~ -~ \frac{m\bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi Q_{JT} }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} +~ \frac{\bar\sigma}{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\bar\sigma \rho_0 \varpi }{D} \cdot \biggl[ \frac{\partial Q_{JT} }{\partial \varpi}\biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] \biggr\}Q_{JT} ~ + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~ -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \frac{\partial Q_{JT}}{\partial\varpi} -~ \frac{m\bar\sigma Q_{JT} }{\varpi} \frac{\partial}{\partial\varpi} \biggl\{ \frac{\rho_0 \varpi }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\} +~ {\bar\sigma}^2 \biggl(\frac{\partial Q_{JT} }{\partial \varpi}\biggr) \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) +~ \frac{\bar\sigma}{\varpi}\frac{\rho_0 }{D} \cdot \frac{\partial Q_{JT} }{\partial \varpi} \biggl[\bar\sigma + m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 +\varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] -~ \frac{\bar\sigma }{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \biggl(\frac{\rho_0 }{D}\biggr)m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \biggr\}Q_{JT} ~ </math> |
|
|
|
<math>~+ \biggl\{ -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) +~ {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) +~ \frac{\bar\sigma}{\varpi}\frac{\rho_0 }{D} \biggl[\bar\sigma + m\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) \biggr] \biggr\}\frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + \bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl[ 2{\dot\varphi}_0 \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] \biggr\}Q_{JT} ~ + {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\bar\sigma\biggl(\frac{m }{\varpi} \biggr) \biggl\{ \frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ 2{\dot\varphi}_0 \biggr] +\frac{\rho_0}{ D} \frac{\partial}{\partial\varpi} \biggl[ \varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] + \biggl[ \varpi \frac{\partial \dot\varphi_0}{\partial\varpi} \biggr] \frac{\partial}{\partial\varpi} \biggl[ \frac{\rho_0}{ D} \biggr] -~ \frac{\partial}{\partial\varpi} \biggl[ \biggl(\frac{\rho_0 }{D}\biggr)\varpi \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr] \biggr\}Q_{JT} ~ </math> |
|
|
|
<math>~+ \biggl\{ \frac{\bar\sigma^2\rho_0}{\varpi D} + \frac{m\bar\sigma \rho_0}{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial\varpi} \biggr) -~ \frac{m\bar\sigma \rho_0 }{D} \biggl( \frac{\partial {\dot\varphi}_0}{\partial \varpi} \biggr) \biggr\}\frac{\partial Q_{JT}}{\partial\varpi} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{ {\bar\sigma}^2 \rho_0^2 }{\gamma P_0} - \frac{{\bar\sigma}^2\rho_0 }{D} \biggl( \frac{m}{\varpi} \biggr)^2 + 2 \bar\sigma {\dot\varphi}_0\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0}{ D} \biggr) \biggr] Q_{JT} ~ + {\bar\sigma}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} +~ \frac{ {\bar\sigma}^2\rho_0 }{D} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\biggl(\frac{\bar\sigma}{\varpi} \cdot \frac{\rho_0}{D}\biggr) \biggl\{ Q_{JT} \cdot \frac{\partial (2m {\dot\varphi}_0 )}{\partial\varpi} ~ + \bar\sigma \cdot \frac{\partial Q_{JT}}{\partial\varpi} \biggr\} \, . </math> |
Each term in the first line of this two-line expression can be found in equation (2.27) of Goldreich, Goodman & Narayan (1986) — which, to facilitate comparison, has been extracted and displayed in the following framed image. But notice that the sign on a number of the terms is flipped. Notice, as well, that neither one of the terms in the second line of our expression appears in equation (2.27) of GGN86.
|
Equations (2.27) and (2.23) extracted without modification from p. 343 of Goldreich, Goodman & Narayan (1986)
"The stability of accretion tori. I - Long-wavelength modes of slender tori"
Monthly Notices of the Royal Astronomical Society, vol. 221, pp. 339-364 © Royal Astronomical Society |
It appears as though the sign on various terms is flipped because GGN86 adopted different sign conventions from Papaloizou & Pringle. Specifically, as is made clear by equation (2.23) of GGN86,
<math>~D~~~\rightarrow ~~~ -D_\mathrm{GGN} \, .</math>
Furthermore, as was deduced above when we compared expressions for the components of the perturbed velocity,
<math>~\bar\sigma~~~\rightarrow ~~~ -\sigma_\mathrm{GGN} \, .</math>
Making this pair of substitutions, our derived two-line expression becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[ \frac{ \sigma_\mathrm{GGN}^2 \rho_0^2 }{\gamma P_0} + \frac{\sigma_\mathrm{GGN}^2\rho_0 }{D_\mathrm{GGN}} \biggl( \frac{m}{\varpi} \biggr)^2 + 2 \sigma_\mathrm{GGN}{\dot\varphi}_0\biggl(\frac{m }{\varpi} \biggr) \frac{\partial}{\partial\varpi} \biggl( \frac{\rho_0}{ D_\mathrm{GGN}} \biggr) \biggr] Q_{JT} ~ - \sigma_\mathrm{GGN}^2 \frac{\partial}{\partial\varpi} \biggl(\frac{\rho_0 }{D_\mathrm{GGN}}\biggr) \frac{\partial Q_{JT}}{\partial\varpi} -~ \frac{ \sigma_\mathrm{GGN}^2\rho_0 }{D_\mathrm{GGN}} \biggl(\frac{\partial^2 Q_{JT} }{\partial \varpi^2}\biggr) + \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial Q_{JT} }{\partial z} \biggr) </math> |
|
|
|
<math>~+\biggl(\frac{\sigma_\mathrm{GGN}}{\varpi} \cdot \frac{\rho_0}{D_\mathrm{GGN}}\biggr) \biggl\{ Q_{JT} \cdot \frac{\partial (2m {\dot\varphi}_0 )}{\partial\varpi} ~ - \sigma_\mathrm{GGN} \cdot \frac{\partial Q_{JT}}{\partial\varpi} \biggr\} \, , </math> |
and the first line appears to exactly match equation (2.27) from GGN86. In an effort to explain why the pair of terms in the second line of our expression do not appear in the GGN86 equation, we quote directly from the text that immediately follows equation (2.27) in Goldreich, Goodman & Narayan (1986): "This is very similar to equation (2.19) for <math>~W = Q/\sigma</math> derived in PPII. The few small differences can be traced to our neglect of the azimuthal curvature of the torus through our Cartesian approximation. These terms are not important and so we expect equation (2.27) to capture all the essential physics of the narrow torus."
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |