User:Tohline/Apps/HayashiNaritaMiyama82
Rotationally Flattened Isothermal Structures

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Hayashi, Narita & Miyama (1982; hereafter HNM82) discovered an analytic solution to the equations that govern the structure of rotationally flattened, self-gravitating isothermal gas clouds. Their solution describes a family of centrally condensed models whose degree of flattening ranges from a spherical structure to an infinitesimally thin disk. For several reasons, I consider this to be one of the most remarkable discoveries — and, hence, one of the most significant papers — related to the structure of self-gravitating systems that was published in the decade of the '80s. First, as has been remarked earlier, there is no particular reason why one should guess ahead of time that the equilibrium properties of any rotating, self-gravitating configuration should be describable in terms of analytic functions. When dealing with compressible equations of state, such analytic solutions are rare even in the context of spherically symmetric structures, so it is impressive that HNM82 found a solution for rotationally flattened, isothermal configurations. Second, about six months earlier the same year, Alar Toomre (1982) published an independent discovery and strikingly independent derivation of exactly the same family of rotationally flattened, isothermal models.1 Third, these two independent derivations were motivated by a desire to better understand two quite different astrophysical environments: The research of HNM82 was focused on star-forming gas clouds while Toomre's research was focused on the structure of elliptical galaxies and the dark-matter halos around spiral galaxies.
Despite my assertion that HNM82 is one of the most significant papers to be published over the past few decades, citation indexes reveal that it is not widely referenced. In large part I attribute this to the fact that HNM82 was published in a Japanese journal (Progress of Theoretical Physics) that has only fairly recently made its archival articles available to the open-access, Astrophysics Data System.
Governing Relations
As has been derived elsewhere, for axisymmetric configurations that obey a barotropic equation of state, hydrostatic balance is governed by the following algebraic expression:
<math>~H + \Phi_\mathrm{eff} = C_\mathrm{B} ,</math>
where <math>~C_\mathrm{B}</math> is the Bernoulli constant,
<math>~\Phi_\mathrm{eff} \equiv \Phi + \Psi ,</math>
and <math>\Psi</math> is the relevant centrifugal potential. For self-gravitating configurations, this algebraic expression must be satisfied in concert with a self-consistent solution of the Poisson equation, which for axisymmetric configurations may be written as,
<math>
~\frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho .
</math>
Supplemental Relations
Following HNM82, we supplement the above-specified set of governing equations with an isothermal equation of state,
<math> ~P = c_s^2 \rho , </math>
where <math>~c_s</math> is the sound speed. Hence, to within an additive constant, the relevant expression for the enthalpy is,
<math> ~H = \int \frac{dP}{\rho} = c_s^2 \ln\biggl(\frac{\rho}{\rho_0}\biggr) . </math>
Also following HNM82, we impose a steady-state velocity flow-field that is described by a fluid with uniform rotational velocity, <math>v_\varphi</math>. Drawing from our table of example Simple rotation profiles, the centrifugal potential that describes this chosen flow-field is given by the expression,
<math> ~\Psi(\varpi) = - v_\varphi^2 \ln\biggl(\frac{\varpi}{\varpi_0}\biggr) . </math>
Summary
In summary, for the particular structures of interest to HNM82, the algebraic relation governing hydrostatic balance is,
<math> \Phi(\varpi,z) = C_\mathrm{B} - c_s^2 \ln\biggl[\frac{\rho(\varpi,z)}{\rho_0}\biggr] + v_\varphi^2 \ln\biggl(\frac{\varpi}{\varpi_0}\biggr) . </math>
This must be solved in conjunction with the Poisson equation, which specifies the second key relationship between <math>~\Phi</math> and <math>~\rho</math>, namely,
<math>
\frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi(\varpi,z)}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi(\varpi,z)}{\partial z^2} = 4\pi G \rho(\varpi,z) .
</math>
Solution
Rationalizing the Approach
HNM82 provide a very clear and detailed description of the approach that they took to solving the above-identified set of simplified governing relations. (Note that Hayashi is credited with deriving the analytic solution.) In very general terms, one can understand the thought process that must have been going on in Hayashi's mind:
- For an isothermal gas cloud, the enthalpy is necessarily a logarithmic function of the density.
- For spherically symmetric, isothermal configurations, a solution to the governing relations exists in which <math>~\rho</math> can be expressed as a power-law function of the radius, specifically, <math>~\rho \propto r^{-2}</math>; hence, the enthalpy displays a logarithmic dependence on the distance.
- Although one could attempt to derive equilibrium structures having a wide range of Simple rotation profiles, it would seem wisest to select a centrifugal potential function that at least has the same form as the enthalpy; hence, the choice was made to impose <math>~v_\varphi = \mathrm{constant}</math> so that, like the enthalpy, the centrifugal potential would exhibit a logarithmic dependence on the distance.
- Three birds, so to speak, can be killed with one stone by guessing a 2D equilibrium density profile of the form <math>~\rho(\varpi,z) = g(\varpi,z)/\varpi^{2}</math>: The <math>~\varpi^{-2}</math> dependence can be combined strategically with <math>~\varpi^{-2}</math> dependence of the centrifugal potential; although it depends on <math>\varpi</math> instead of <math>r</math>, the density profile will at least resemble the spherical solution; and — certainly the most critical realization — the Poisson equation, which for this problem is a 2D elliptic PDE, can be rewritten as a 1D ODE and solved analytically!
HNM82 Derivation
HNM82 guess a density distribution of the form (see their Eq.2.3),
<math> ~\frac{\rho(\varpi,z)}{\rho_0} = g(\varpi,z) \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-2} . </math>
The algebraic expression defining hydrostatic balance then becomes,
<math> ~\Phi(\varpi,z) = C_\mathrm{B} - c_s^2 \ln g(\varpi,z) + (2c_s^2 + v_\varphi^2) \ln\biggl(\frac{\varpi}{\varpi_0}\biggr) ; </math>
and, after multiplying both sides by <math>~\varpi^2</math>, the Poisson equation becomes,
<math>
~\varpi \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi(\varpi,z)}{\partial\varpi} \biggr] + \varpi \frac{\partial}{\partial z} \biggl[ \varpi \frac{\partial \Phi(\varpi,z)}{\partial z} \biggr] = (4\pi G\rho_0 \varpi_0^2) g(\varpi,z) .
</math>
Plugging the expression for <math>~\Phi</math> into the Poisson equation gives (see Eq. 2.4 of HNM82),
<math>
~\varpi \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \ln g(\varpi,z)}{\partial\varpi} \biggr] + \varpi \frac{\partial}{\partial z} \biggl[ \varpi \frac{\partial \ln g(\varpi,z)}{\partial z} \biggr] = - \biggl[ \frac{4\pi G\rho_0 \varpi_0^2}{c_s^2} \biggr] g(\varpi,z) .
</math>
HNM82 realized that since this equation "is invariant to the scale changes of both <math>~\varpi</math> and <math>~z</math>, it has a conformal solution such that <math>~g</math> is a function of <math>~z/\varpi</math> alone." In particular, as HNM82 pointed out, by making the substitution,
<math> ~\zeta \equiv \sinh^{-1}\biggl(\frac{z}{\varpi}\biggr)= \ln \biggl[ \frac{r+z}{\varpi} \biggr] , </math>
the above, 2D elliptic PDE (Poisson equation) can be written as the following, 1D second-order ODE:
<math> ~\frac{d^2\ln g(\zeta)}{d\zeta^2} = - \biggl[ \frac{4\pi G\rho_0 \varpi_0^2}{c_s^2} \biggr] g(\zeta) . </math>
As presented by HNM82, the solution to this Poisson equation that meets the most physically reasonable boundary conditions at <math>~\zeta = 0</math> (i.e., <math>~g</math> is finite and <math>~dg/d\zeta = 0</math>) is,
<math> ~g(\zeta) = \biggl[ \frac{c_s^2}{2\pi G\rho_0 \varpi_0^2} \biggr] \frac{\gamma^2}{\cosh^2(\gamma\zeta)} , </math>
where <math>~\gamma = [1 + v_\varphi^2/(2c_s^2)]</math> is a parameter that identifies an individual equilibrium structure from the family of allowed solutions.
Structural Properties
By analogy with the solution that was derived for a spherically symmetric isothermal structure with a power-law density distribution, we can associate the scale length <math>~\varpi_0</math> with the characteristic density <math>~\rho_0</math> at that location through the relation,
<math> ~\rho_0 = \frac{c_s^2}{2\pi G \varpi_0^2 } , </math>
in which case we can write,
<math> ~g(\zeta) = \frac{\gamma^2}{\cosh^2(\gamma\zeta)} . </math>
With this definition in hand, the equilibrium models discovered by HNM82 exhibit the following properties.
- Density Distribution:
- Confirming the expression presented as Eq. (3.1) in HNM82, the 2D density distribution for models with different values of the dimensionless parameter <math>~\gamma</math> is,
|
<math> ~\rho(\varpi,z) </math> |
<math> ~= </math> |
<math> ~\rho_0 g(\varpi,z) \biggl(\frac{\varpi}{\varpi_0}\biggr)^{-2} </math> |
|
|
<math> ~= </math> |
<math> ~\biggl[ \frac{c_s^2}{2\pi G \varpi_0^2} \biggr]\biggl(\frac{\varpi_0}{\varpi}\biggr)^{2} \frac{\gamma^2}{\cosh^2(\gamma\zeta)} . </math> |
- Gravitational Potential:
- As presented in Eq. (3.4) of HNM82, to within an additive constant the 2D potential distribution for models with different values of the dimensionless parameter <math>~\gamma</math> is,
|
<math> ~\frac{\Phi(\varpi,z)}{2c_s^2} </math> |
<math> ~= </math> |
<math> ~\frac{C_\mathrm{B}}{2c_s^2} - \frac{1}{2} \ln g(\varpi,z) + \biggl(1 + \frac{v_\varphi^2}{2c_s^2} \biggr) \ln\biggl(\frac{\varpi}{\varpi_0}\biggr) </math> |
|
|
<math> ~= </math> |
<math> ~\frac{C_\mathrm{B}}{2c_s^2} - \frac{1}{2} \ln \biggl[ \frac{\gamma^2}{\cosh^2(\gamma\zeta)} \biggr] + \gamma \ln\biggl(\frac{\varpi}{\varpi_0}\biggr) </math> |
|
|
<math> ~= </math> |
<math> ~\frac{C_\mathrm{B}}{2c_s^2} + \ln \biggl[ \frac{1}{\gamma} \biggr] + \ln \biggl[ \cosh (\gamma\zeta) \biggr] + \ln\biggl(\frac{\varpi}{\varpi_0}\biggr)^\gamma </math> |
|
|
<math> ~= </math> |
<math> ~C' + \ln \biggl[ \varpi^\gamma \cosh (\gamma\zeta) \biggr] . </math> |
- HNM82 point out that this last expression also can be written in terms of <math>~r</math> and <math>~z</math> as follows:
|
<math> ~\frac{\Phi(\varpi,z)}{2c_s^2} </math> |
<math> ~= </math> |
<math> ~C' + \ln \biggl[ \frac{1}{2}(r+z)^\gamma + \frac{1}{2}(r-z)^\gamma \biggr] . </math> |
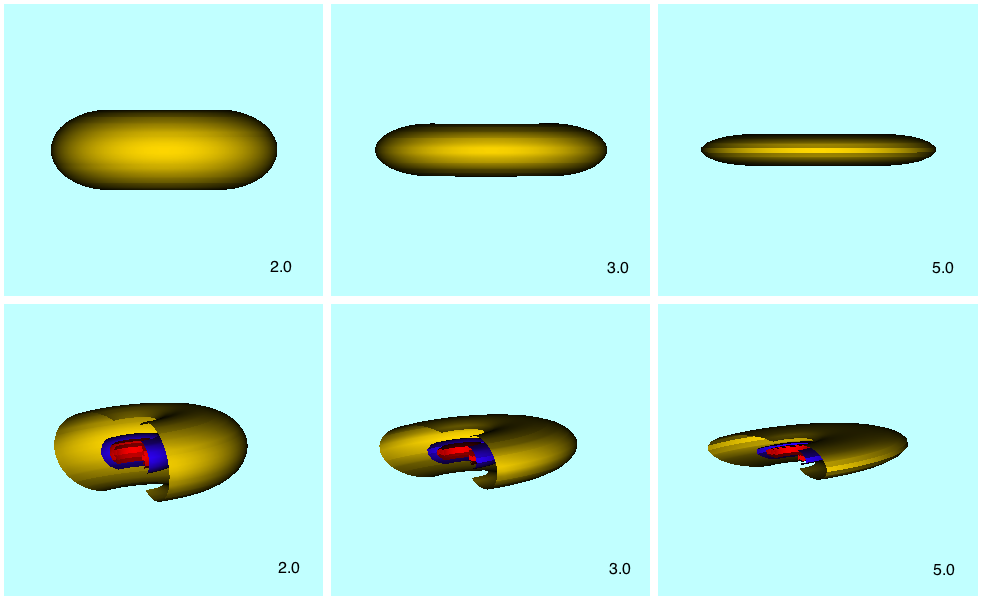
| 3D Renderings of Isothermal Disks from Hayashi, Narita & Miyama (1982) |
|---|
| (Top) Edge-on view of three isothermal disks; (Bottom) Cut-away view of highest-density region of the same three disks. Values of flattening parameter, <math>~\gamma</math>, shown in bottom-right corner of each frame. |
Footnotes
- At the end of their paper, HNM82 present the following Note added in proof: "After we submitted this paper, a paper by Toomre (Astrophys. J. 259 (1982), 535) appeared. He also found the same solutions as Eq. (2.3), although he did not study the stability of the equilibrium configurations."
See Also
- I. Hachisu & Y. Eriguchi (1985), Astronomy & Astrophysics, 143, 355: Equilibrium structures of rotating isothermal gas clouds. I.
- I. Hachisu & Y. Eriguchi (1985), Astronomy & Astrophysics, 147, 13: Equilibrium structures of rotating isothermal gas clouds. II — Dependence on the angular momentum distribution
- M. Kiguchi, S. Narita, S. M. Miyama & C. Hayashi (1987), ApJ, 317, 830: The Equilibria of Rotating Isothermal Clouds
- M. Kiguchi, S. Narita, S. M. Miyama & C. Hayashi (1988), Progress in Theoretical Physics, 96, 50: Chapter 4. The Equilibrium and the Stability of Rotating Isothermal Clouds

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |