User:Tohline/Appendix/Ramblings/Saturn
Saturn
Here we draw heavily from the review by L. Spilker (14 June 2019) titled, Cassini-Huygens' exploration of the Saturn system: 13 years of discovery that has appeared in Science, Vol. 364, Issue 6445, pp. 1046 - 1051. This review reminds us to emphasize that, although virtually all of the chapters of our H_Book have been written from the standpoint of analyzing the structure, stability, and dynamics of stars, much of our discussion is applicable in a fairly straightforward manner to studies of planets — especially the gas giants — because they are also self-gravitating fluids.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Structure and Stability
Excerpt from the first paragraph on p. 1050 of L. Spilker (2019):
|
Saturn's ring system acts like a seismograph, providing a measure of Saturn's internal oscillations (or normal modes) that directly probe the interior of the planet … and provide a means for measuring its deep rotation rate. These vibrations, determined by Saturn's nonuniform internal structure, are probably driven by convection inside the planet, which cause oscillations in Saturn's gravity field … Preliminary modeling of the propagation behavior of this collection of waves provides an interior rotation rate for Saturn of ∼ 10.6 hours … See also:
|
Excerpts from the article by L. Iess et al. (2019), Science, Vol. 364, Issue 6445, p. 1052 titled, Measurement and implications of Saturn's gravity field and ring mass:
|
… the mass distribution inside a fluid and rapidly rotating planet like Saturn is largely driven by the ratio between centrifugal and gravitational forces. In static conditions, the planet should rotate uniformly and its gravity field should be axially and hemispherically symmetric and thus described by zonal harmonics.
|
Hexagon Storm
Excerpt from the the subsection titled "Saturn" on p. 1049 of L. Spilker (2019):
|
Saturn's alternating eastward and westward jet streams define the bands of cloud that circle the planet … One of the jet streams near 75° north latitude, forms a hexagonal pattern that is two Earth diameters across … Voyager first discovered the hexagon, and it is still there after 35 years … this hexagonal-shaped jet stream … is remarkable for its stability and longevity; its source remains a mystery. See also:
|
| FIGURE 1 | FIGURE 2 |
|---|---|
|
FIGURE 1: obtained from this NASA Newsletter; FIGURE 2: obtained from this NASA/JPL site. |
|
Binary Mass-Transfer
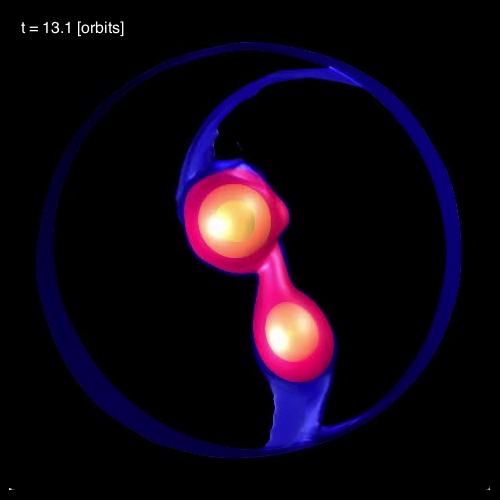
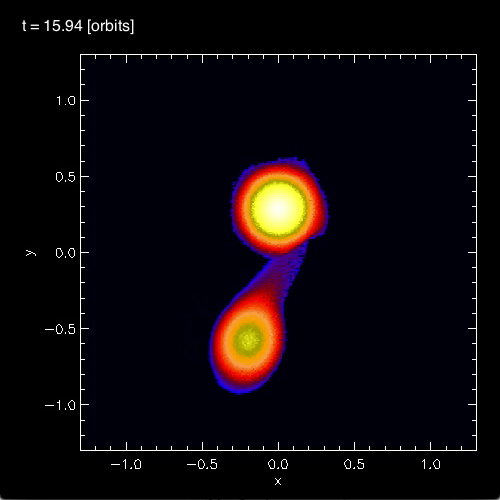
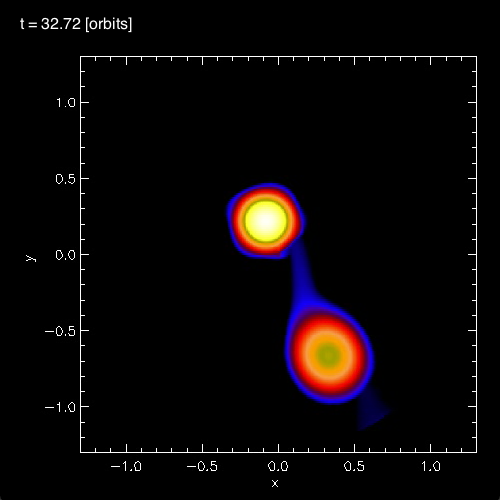
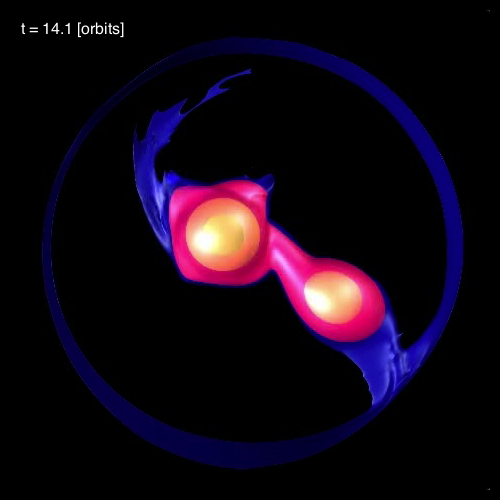
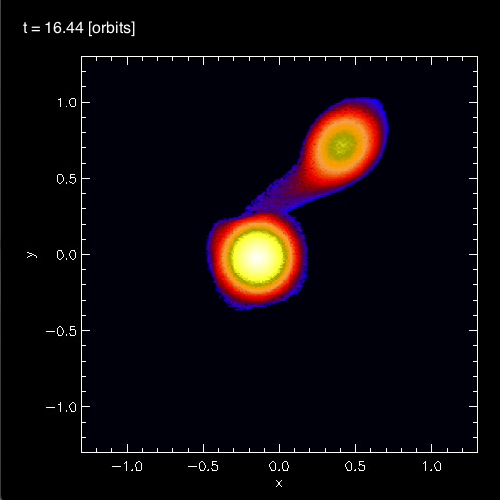
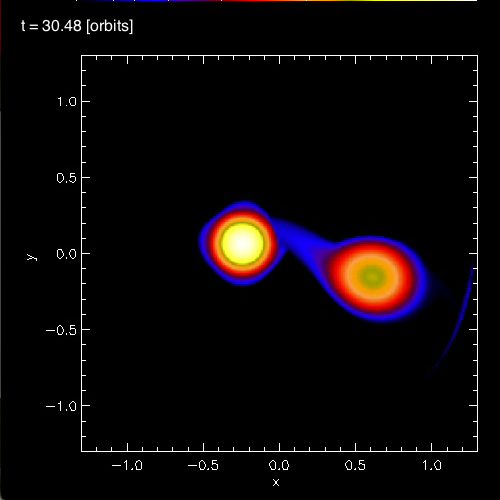
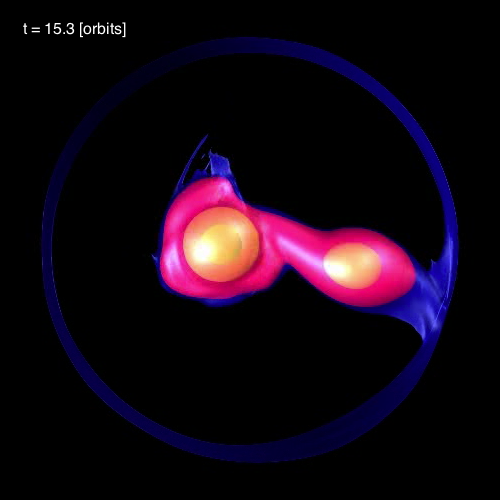
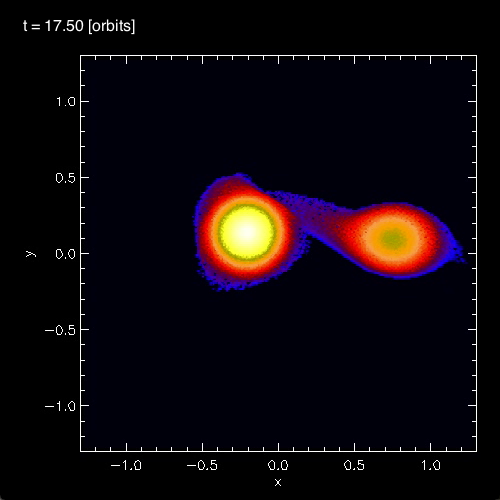
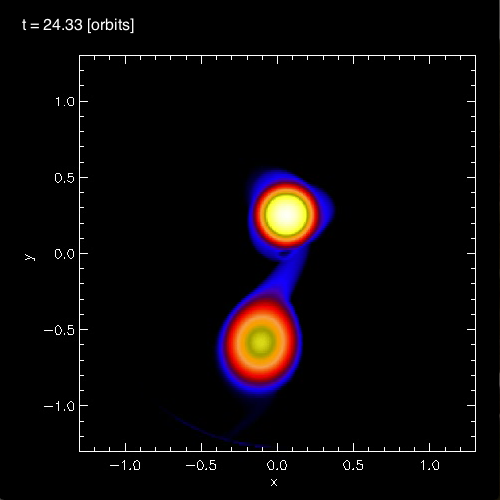
In connection with our own efforts to realistically model dynamical, mass-transfer events in close binary systems, we have noticed the spontaneous development of standing waves in the equatorial regions of the accreting star. As is illustrated in Figure 3, below, during each of the three cited model evolutions (A, B, and C) we have identified standing waves that are very clearly 3-sided (triangular; bottom row of Figure 3), 4-sided (box-shaped; middle row of Figure 3), or 5-sided (pentagonal; top row of Figure 3). In association with our published discussion of each of these three evolutions — relevant links are provided at the top of each Figure column — an animation sequence has been provided that shows the model's time-evolutionary behavior. (Evolution A has been followed through 15.3 P0; evolution B has been followed through 18.3 P0; and evolution C has been followed through 34.0 P0, where P0 is the associated model's initial binary orbital period.) If you watch any one of these evolutions, you will see the smooth development of these nonlinear-amplitude, standing-wave structures in sequence. Looking closely, at an appropriate time in each evolution, you should also be able to identify the development of a (low-amplitude) standing wave structure that has 6 sides; that is, a hexagonal standing wave. We have wondered whether the physical processes that conspire to resonately excite a hexagonal-shaped standing wave in our binary mass-transfer simulations is related to the physical processes that are responsible for creating and sustaining the hexagonal-shaped storm in Saturn's northern hemisphere.
| FIGURE 3: Nonlinear-Amplitude Distortions that Develop in Three Separate Model Evolutions | ||
|---|---|---|
| Evolution A | Evolution B | Evolution C |
|
MFTD (2007) |
MFSCFEDT (2017) |
MFSCFEDT (2017) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| †The evolution identified here as Model Q0.5P_G1 was first discussed in §5.2 of DMTF (2006), wherein it was identified as Model Q0.5-Da; the caption to Figure 7 of that paper contains a link to an (mpeg_file = video3-2.mpg) animation that presents a 3D rendering of this model's evolution. | ||
Several key references:
- [Paper DMTF (2006)] M. C. R. D'Souza, P. M. Motl, J. E. Tohline & J. Frank (2006), ApJ, 643, p. 381: Numerical Simulations of the Onset and Stability of dynamical Mass Transfer in Binaries
- [Paper RPA (2007)] É. Racine, E. S. Phinney & P. Arras (2007), MNRAS, 380, 381: Non-dissipative tidal synchronization in accreting binary white dwarf systems
- [Paper MFTD (2007)] P. M. Motl, J. Frank, J. E. Tohline & M. C. R. D'Souza (2007), ApJ, 670, p. 1314: The Stability of Double White Dwarf Binaries Undergoing Direct-Impact Accretion
- [Paper MFSCFEDT (2017)] P. M. Motl, J. Frank, J. Staff, G. C. Clayton, C. L. Fryer, W. Even, S. Diehl & J. E. Tohline (2017), ApJSuppl., Vol. 229, Issue 2, article id. 27, 41 pp.: A Comparison of Grid-based and SPH Binary Mass-transfer and Merger Simulations
The following discussion has largely been extracted from §3.1.4 (p.29) of MFSCFEDT (2017):
|
In §4 of their paper, MFTD (2007) point out that in the vicinity of the accretor some of the models developed nonlinear-amplitude "equatorial distortions with [azimuthal mode numbers] 6 ≥ m ≥ 3." As is illustrated by the trio of images displayed in the bottom row of Figure 3, above, at a certain point (or points) in each of these binary mass-transfer evolutions … the disk surrounding the accretor has a triangular shape … presumably associated with the excitation of an m = 3 mode. This trio of triangular shaped images come from, respectively, evolutionary times: (A, B, C)m=3 = (15.3P0, 17.50P0, 24.33P0). Similarly, the trio of images displayed in the middle row of Figure 3 show the excitation of an m = 4 (box-shaped) mode at evolutionary times: (A, B, C)m=4 = (14.1P0, 16.44P0, 30.48P0). And the trio of images displayed in the top row of Figure 3 show the excitation of an m = 5 (pentagonal-shaped) mode at evolutionary times: (A, B, C)m=5 = (13.1P0, 15.94P0, 32.72P0).
|
The following discussion has largely been extracted from §4 (esp. pp. 1322-1324) of MFTD (2007):
|
… RPA (2007) discussed the possibility that a resonance condition between the orbital frequency and the eigenfrequencies of some of the generalized r-modes in the accretor star saturates its spin and channels rotational kinetic energy into oscillation modes. This translates into a dissipationless torque that is capable of returning the spin angular momentum back to the orbit and thus increasing the efficiency of tidal coupling. The fact that in our nonlinear simulations the change in the spin of the accretor is coupled to the dynamics of the binary and that we see equatorial distortions with 6 ≥ m ≥ 3 … seem at first sight to suggest that these modes play a role. However, when examined in detail, there are some aspects of the evolution that are inconsistent with [this] interpretation.
|
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |

