Difference between revisions of "User:Tohline/Appendix/Ramblings/RiemannMeetsOculus"
| Line 868: | Line 868: | ||
<font color="darkgreen"><b>MultiLagrange20.dae</b></font>: | <font color="darkgreen"><b>MultiLagrange20.dae</b></font>: | ||
<br />In this model, we show the motion of six Lagrange particles. <font color="red">This works in both visualization venues!</font> | <br />In this model, we show the motion of six Lagrange particles. <font color="red">This works in both visualization venues!</font> | ||
</li> | |||
<li> | |||
<font color="darkgreen"><b>MultiLagrange21.dae</b></font>: | |||
<br />Make all six of the Lagrangian "red cube" markers smaller. | |||
</li> | </li> | ||
</ul> | </ul> | ||
Revision as of 00:16, 28 May 2020
Rebuild Riemann S-Type Ellipsoid Inside Oculus Rift S Environment

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Preamble
In an accompanying discussion, we have illustrated how an animated, interactive 3D scene can be largely defined via the xml-formatted language named COLLADA. In the last major subsection of that discussion, we have outlined the steps that can be followed to specifically generate any of a variety of Riemann S-Type ellipsoids. These steps were identified within the context of our effort to construct 3D VR/AR models that could be faithfully rendered using the Mac's Preview app.
In a separate but closely connected discussion, we have demonstrated that most of our COLLADA-based models can be imported into the 3D virtual-reality environment of the Oculus Rift S. Toward the end of this separate discussion, we provide the full COLLADA code — in a plain text format — along with a summary description of a model that has been assigned the name, FullLast45X.dae.
Intially, we discovered that most of the Riemann S-Type ellipsoids that we developed while relying on the Mac's Preview app did not display properly within the Oculus Rift S environment. What we propose to do, here, is methodically re-construct a variety of our earlier models that were viewable in the "Preview" app in such a way that they are all viewable with the Oculus Rift S. We begin with this "… 45X" model — renaming it, RiemannBuild00.dae. Step by step we will insert components of one of our previously constructed COLLADA-based models of an S-Type Riemann ellipsoid into a <visual_scene> that can be properly executed within the Oculus Rift S.
Assemble Components
-
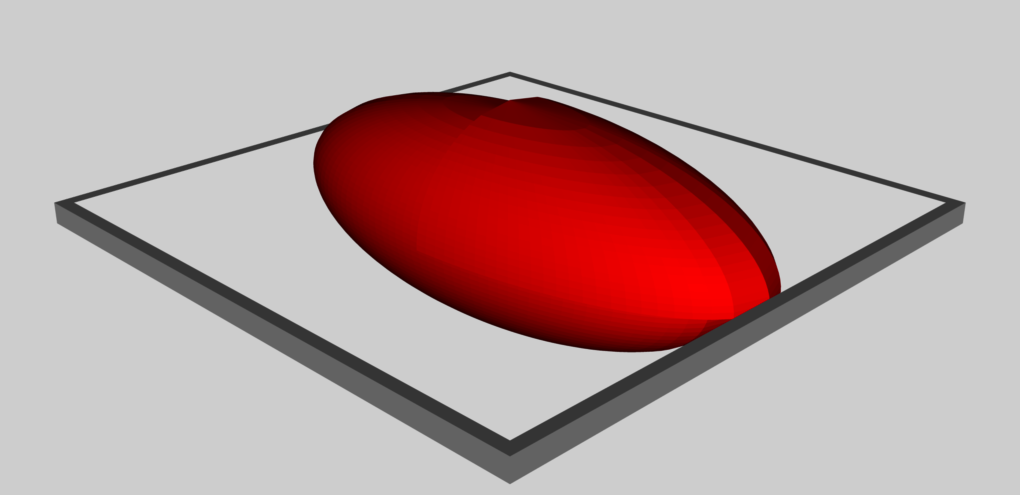
RiemannBuild00.dae:
- This model, with <up_axis>Z_UP></up_axis>, contains a set of purple cubes that lie in the Y0-Z0 plane, and along the inertial frame's X0 axis from -5.0 inches to +5.0 inches; the last purple "cube" (at X0 = +5) is actually a rectangular box whose longest axis is parallel to the Z0 axis.
Mac Preview of RiemannBuild00.dae 
- The scene also includes a red ellipsoid with axis ratios b/a = 0.41 and c/a = 0.385. The "EntireEllipsoid" has been scaled such that its longest ( c ) axis has a length of 4 inches; and it has been translated in the Y0-Z0 plane to a location along the Y0 axis where the center of the ellipsoid is 8.0 inches from the origin of the inertial coordinate system. The ellipsoid's "First" quadrant <node> was, in addition, scaled by (1.1, 1.1, 1.1) in order for it to stick out a bit from the other quadrants to help the viewer decipher its rotational behavior.
<node id="EntireEllipsoid" name="OculusRift_EFE"> <translate>0.0 8.0 0.0</translate> <rotate sid="rotationY">0.0 1.0 0.0 90.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 90.0</rotate> <rotate sid="rotationX">1.0 0.0 0.0 90.0</rotate> <scale sid="scale">4.0 4.0 4.0</scale> <node id="First" name="First_instance_EFE"> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 0.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 0.0</rotate> <scale sid="scale">1.1 1.1 1.1</scale> <instance_node url="#ID3_EFE" /> </node> ... - The default orientation of the "EntireEllipsoid" is <math>~(a, b, c) \Leftrightarrow ~ (X_0, Y_0, Z_0)</math>. But for this model, before the animation starts, the "EntireEllipsoid" is reoriented by turning it 90° in Y, then 90° in Z, then 90° in X; as displayed in the above image, this resulted in an alignment of <math>~(a, b, c) \Leftrightarrow ~ (Y_0, X_0, -Z_0)</math>.
-
The set of <animation> instructions includes a specification that, (1) TIME start at 0.0 seconds and end (one animation loop) at 10.0 seconds; (2) over this time interval, the rotation ANGLE should start at 90° and end at 270° [in COLLADA, it is understood that the ANGLE will vary linearly with TIME, unless explicitly specified otherwise]; and (3) via the <channel/target> instruction, the rotation should be about the longest (rotationX) axis of the ellipsoid.
<float_array id="First_rotation_euler_Y-input-array" count=" 2"> 0.0000 10.0000 </float_array> ... <float_array id="First_rotation_euler_Y-output-array" count=" 2"> 90.0 270.0 </float_array> ... <channel source="#First_rotation_euler_Y-sampler" target="EntireEllipsoid/rotationX.ANGLE"/>
- This model, with <up_axis>Z_UP></up_axis>, contains a set of purple cubes that lie in the Y0-Z0 plane, and along the inertial frame's X0 axis from -5.0 inches to +5.0 inches; the last purple "cube" (at X0 = +5) is actually a rectangular box whose longest axis is parallel to the Z0 axis.
-
RiemannBuild02.dae:
-
Got rid of all of the <visual_scene><nodes> that had been used to create the line of purple "cubes"; set the "EntireEllipsoid" <translate> coordinate to zero in all three dimensions so that the center of the red ellipsoid coincided with the origin of the principal frame of reference; set to zero the values of all three <rotate> ANGLEs for the "EntireEllipsoid" so that the red ellipsoid was initially positioned in its default orientation, that is, <math>~(a, b, c) ~\Leftrightarrow ~(X_0, Y_0, Z_0)</math>;
<node id="EntireEllipsoid" name="OculusRift_EFE"> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 0.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 0.0</rotate> <scale sid="scale">5.0 5.0 5.0</scale> <node id="First" name="First_instance_EFE"> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 0.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 0.0</rotate> <scale sid="scale">1.1 1.1 1.1</scale> <instance_node url="#ID3_EFE" /> </node> ...and set the <animation> parameters such that, over a 10 second interval of time, using the <channel … target="EntireEllipsoid/rotationZ.ANGLE"/> directive the ellipsoid was instructed to spin about the shortest ( c ) axis, from 0° to 180°.
<float_array id="First_rotation_euler_Z-input-array" count=" 2"> 0.0000 10.0000 </float_array> ... <float_array id="First_rotation_euler_Z-output-array" count=" 2"> 0.0 180.0 </float_array> ... <channel source="#First_rotation_euler_Z-sampler" target="EntireEllipsoid/rotationZ.ANGLE"/>
RESULT: Using the Mac's Preview app to view this modified COLLADA file, the (now) isolated red ellipsoid did spin, as desired, through 180° about the ellipsoid's shortest axis. But when imported into the Oculus Rift S environment, the isolated red ellipsoid was spinning about the ellipsoid's longest axis. I don't understand why!
-
Got rid of all of the <visual_scene><nodes> that had been used to create the line of purple "cubes"; set the "EntireEllipsoid" <translate> coordinate to zero in all three dimensions so that the center of the red ellipsoid coincided with the origin of the principal frame of reference; set to zero the values of all three <rotate> ANGLEs for the "EntireEllipsoid" so that the red ellipsoid was initially positioned in its default orientation, that is, <math>~(a, b, c) ~\Leftrightarrow ~(X_0, Y_0, Z_0)</math>;
-
RiemannBuild03.dae:
Here, we implemented only two changes to the COLLADA code: (1) We modified the "EntireEllipsoid" <node>'s "rotationZ" instruction to specify that, prior to implementing the rotation, the ellipsoid should be turned 1° [instead of zero degrees] about the shortest ( c ) axis;
<node id="EntireEllipsoid" name="OculusRift_EFE"> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 0.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 1.0</rotate> <scale sid="scale">5.0 5.0 5.0</scale> ...and (2) inside the set of <animation> instructions, we specified that the time-dependent ANGLE should have a starting (TIME = 0.0) value of 1° and an ending (TIME = 10.0) value of 180°.
<float_array id="First_rotation_euler_Z-output-array" count=" 2"> 1.0 180.0 </float_array> ...
RESULT: The desired behavior — that is, spinning about the shortest ( c ) axis from 1° to 180° — was observed in both the Mac's Preview app and in the Oculus Rift S environment. But I don't actually understand why the Oculus import resulted in two quite different spinning motions, given that the starting ANGLE was only changed from 0° to 1°. -
RiemannBuild05.dae:
Pulling from the file named, b41c385_DI.dae, we added a "MidPlane Frame" to the visual_scene. This worked in the Oculus Rift S environment as well as in the Mac's Preview app (see image immediately below).
| Mac Preview of … | ||
|
RiemannBuild05.dae |
RiemannBuild06.dae |
RiemannBuild09D.dae |
-
RiemannBuild06.dae:
Pulling from the file named, b41c385_DI.dae, we added a "Black Cylindrical Pointer" to the visual_scene. This worked in the Oculus Rift S environment as well as in the Mac's Preview app. -
RiemannBuild09D.dae:
After much trial and error, we have successfully introduced two separate animation instructions. In addition to instructing the visual scene to spin the red ellipsoid about its "c" axis at a specific rate, we can now instruct the visual scene to spin the "MidPlane Frame" about the same axis, but in the opposite direction (at any specified rate), in order to mimic a rotating frame of reference. As the above image from the Mac Preview app shows, we have also added a second "Black Cylindrical Pointer", orienting it in the positive Z0 direction; and we have removed the special scaling of the "First" quadrant of the ellipsoid that had been introduced in earlier models to break the geometric symmetry of the object, thereby helping us to keep track of changes in the model's spin directions and rates. - RiemannBuild09G.dae: Fixed the way the second "Black Cylindrical Pointer" is handled.
|
-
Mac Preview of
RiemannLagrange12L.dae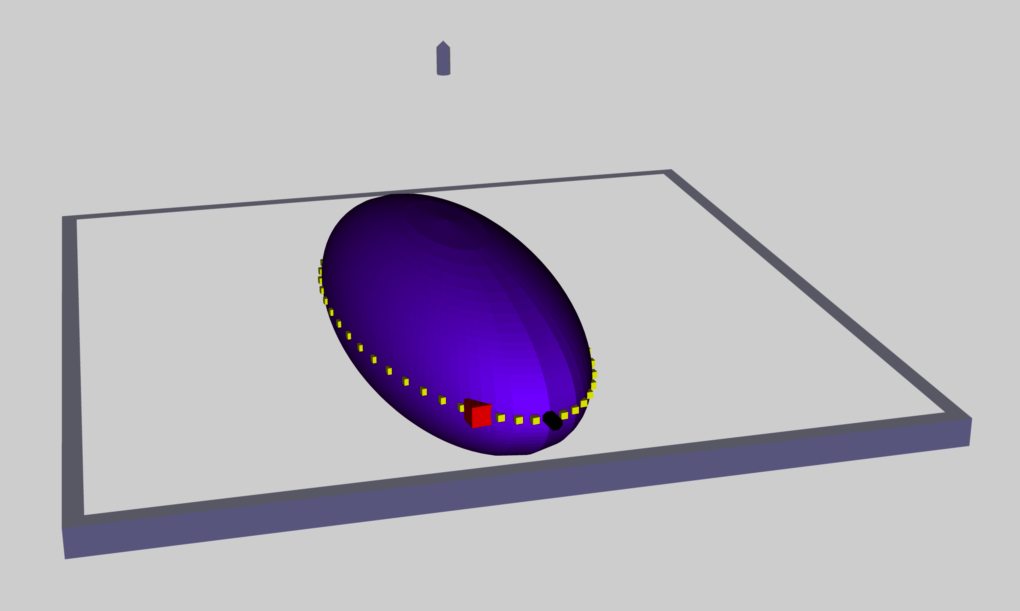
RiemannBuild10C.dae:
Hold the red ellipsoid completely still at ANGLE = 0° while the MidPlane Frame spins briskly clockwise. In addition to typing in the floating-point value, 0.0, a dozen times to correlate with the twelve different specified increments of TIME, we also changed the initial value of "rotationZ" from "4.0" to "0.0" inside the "EntireEllipsoid" <node>.
RESULT: Seems to work in both visualization venues. -
RiemannLagrange11B.dae:
Insert 51 small yellow (cube) "Markers" in the equatorial plane and on the surface of the red ellipsoid to identify the trajectory of a Lagrangian fluid element. -
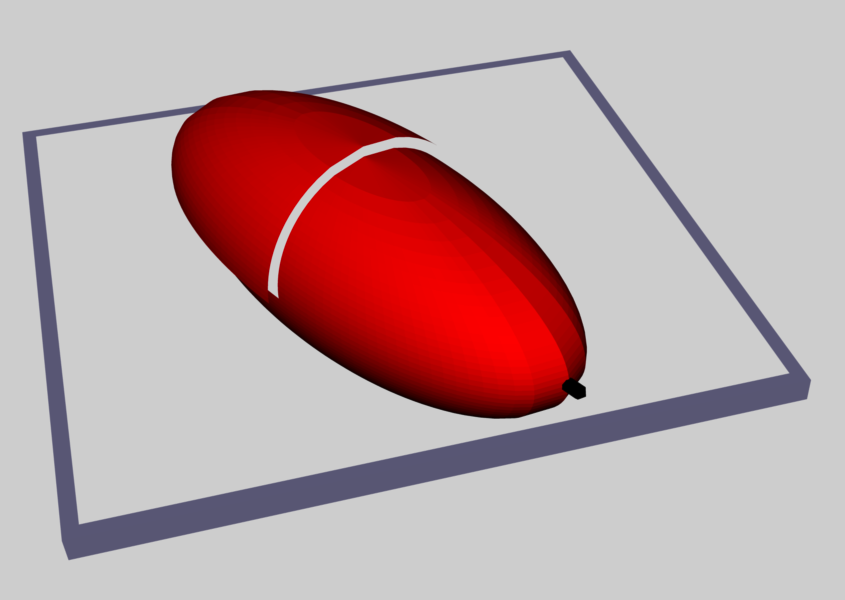
RiemannLagrange12L.dae (rotating frame):
Include one solitary Lagrangian fluid element (red marker that is a bit larger than the previously inserted small yellow cubes), showing its "retrograde" motion in the equatorial plane and on the surface of the — now opaque, purple — ellipsoid (see Mac Preview image shown here, on the right). In this model, the displayed time-dependent behavior — the spinning "MidPlane Frame" and the red Lagrangian fluid marker — is quantitatively correct for an S-Type Riemann ellipsoid that has the specific principal axis ratios — that is, b/a = 0.41 and c/a = 0.385 — of the displayed purple ellipsoid, and that is being viewed from a rotating frame of reference in which the ellipsoid is stationary.
There is still a funny issure related to the "Zup Pointer". Over time, it gains a bit of tilt. -
RiemannLagrange12M.dae (inertial frame):
In an effort to diagnose/deal with the "Zup Pointer" issue (see RiemannLagrange12L.dae), this model attempts to move to the inertial frame of reference. The Zup Pointer appears to remain stationary, and pointed precisely the desired direction. This model (or maybe it was model …14P) does not import properly into the Oculus Rift. I can see the model, but Oculus outlines the scene in red, and displays red exclamation marks, to indicate that it does not like what the conversion routine has generated. -
RiemannLagrange14Q.dae (inertial frame):
My guess is that the Oculus Rift (or the KG's conversion routine) has a problem dealing with the coordinate singularity along the Z-axis — that is, all longitudes lines reach the pole of the spherical coordinate system at the same (or at an undetermined value of the) azimuthal angle. So, instead of using the geometric object [the "Cylindrical Pointer"] that was created to highlight the negative X-axis of the ellipsoid, here we are identifying the Z_0 axis by stretching the "Cube" geometric object into a "long" thin solid rectangle and placing it along the Z_0 axis. This new "Zup Pointer" seems to work in both visualization venues.
S-Type Ellipsoid b41c385
Here — as one specific example — we will continue to focus on the direct (as opposed to the adjoint) S-Type Riemann ellipsoid whose axis ratios are b/a = 0.41 and c/a = 0.385. Additional physical properties of this configuration are detailed in an accompanying discussion.
Let's add the wall clock and alpha-numeric identification of the model's parameters. To start with, we have made a copy of "RiemannLagrange12L.dae" and renamed it, b41c385Rot00.dae
Post Alpha-Numeric Information
-
b41c385Rot02.dae (rotating frame):
First, we inserted just the "equal" sign and did not mix it in with the animated "MidPlane Frame." We were able to view this model inside the Oculus Rift S environment, as well as with the Mac's Preview app. -
b41c385Rot05.dae (rotating frame):
This appears to be the best way to handle the rotating frame when the inertial-frame spin of the ellipsoid is counter-clockwise — hence, the rotating "Frame" spin should be clockwise.- The "MidPlane" <animation> specification should be entirely in terms of positive angles; for example,
<!-- This sets the spin rate of the "MidPlane" Frame of reference --> <source id="Frame_rotation_euler_Z-output"> <float_array id="Frame_rotation_euler_Z-output-array" count="31"> 3.0 63.0 123.0 183.0 ... 1683.0 1743.0 1803.0 </float_array> <technique_common> <accessor source="#Frame_rotation_euler_Z-output-array" count="31" stride="1"> <param name="ANGLE" type="float"/> </accessor> </technique_common> </source> - The relevant <channel> specification should be target="Inertial/rotationZ.ANGLE".
-
The overarching parent <node id="Inertial" …> should flip every child node that is part of the laboratory infrastructure by 180° about the X-axis, then begin the clockwise rotation by specifying the initial "rotationZ" = 3.0, to match the initial spin angle specified in the <animation>. In this example, we have …
<node id="Inertial" name="instance_inertial"> <!-- Start Inertial Grouping of Objects --> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 180.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 3.0</rotate> <scale sid="scale">1.25 1.25 1.25</scale> <node id="Zup_Pointer" name="instance_zupPointer"> <translate>0.0 0.0 -5.0</translate> <rotate sid="rotationX">1 0 0 0.0</rotate> <rotate sid="rotationY">0 1 0 0.0</rotate> <rotate sid="rotationZ">0 0 1 0.0</rotate> <scale sid="scale">0.125 0.5 1.5</scale> <instance_node url="#ZupPointer" /> </node> <!-- instance: MidPlane Frame (MidPlane flips with rotationX = 180 for clockwise spin)--> <node id="MidPlane" name="instance_MidPlane"> <translate>0.0 0.0 0.0</translate> <rotate sid="rotationX">1.0 0.0 0.0 0.0</rotate> <rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate> <rotate sid="rotationZ">0.0 0.0 1.0 0.0</rotate> <scale sid="scale">1.25 1.25 1.25</scale> <instance_node url="#EqPlane" /> </node> <!-- BEGIN LABELING HERE --> <node name="Labels"> <translate>7.5 -2.0 -5.0</translate> <rotate sid="rotationX">1 0 0 0</rotate> <rotate sid="rotationY">0 1 0 0</rotate> <rotate sid="rotationZ">0 0 1 180</rotate> <scale sid="scale">0.1 0.1 0.1</scale> <!-- Equals sign #1 --> <node name="Equals1"> <translate>0.0 15.0 1.0</translate> <rotate sid="rotationX">1 0 0 0</rotate> <rotate sid="rotationY">0 1 0 0</rotate> <rotate sid="rotationZ">0 0 1 0</rotate> <scale sid="scale">1.0 1.0 1.0</scale> <node id="IDd51" name="instance_51"> <matrix>0.25 0 0 0.0 0 1 0 0.0 0 0 1 2.4 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> <node id="IDd52" name="instance_52"> <matrix>0.25 0 0 0.0 0 1 0 1.1 0 0 1 2.4 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> <node id="IDd53" name="instance_53"> <matrix>0.25 0 0 0.0 0 1 0 2.2 0 0 1 2.4 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> <node id="IDd55" name="instance_55"> <matrix>0.25 0 0 0.0 0 1 0 0.0 0 0 1 4.2 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> <node id="IDd56" name="instance_56"> <matrix>0.25 0 0 0.0 0 1 0 1.1 0 0 1 4.2 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> <node id="IDd57" name="instance_57"> <matrix>0.25 0 0 0.0 0 1 0 2.2 0 0 1 4.2 0 0 0 1.0</matrix> <instance_node url="#LettersID3" /> </node> </node> </node> <!-- END LABELING HERE --> </node> <!-- End Inertial Grouping of Objects --> - Also, the "Zup_Pointer" <node> and the overarching "Labels" <node> should be translated by Z = -5.0, instead of the normal Z = +5.0 translation.
This appears to work in both visualization venues. We appreciate, however, that we almost certainly will have to insert some additional translations when the rest of the LABELing is included because we suspect that the "Equals" sign is actually written backwards, given that only a translation in Z has been invoked thus far.
- The "MidPlane" <animation> specification should be entirely in terms of positive angles; for example,
-
b41c385Rot08.dae (rotating frame):
This model contains all of the alpha-numeric labeling that we previously constructed for this particular S-Type Riemann ellipsoid. As it turns out, all we needed to do additionally in order to rectify the orientation of the labels was to spin the whole signage by 180° about the X-axis.<!-- BEGIN LABELING HERE --> <node name="Labels"> <translate>7.5 -2.0 -5.0</translate> <rotate sid="rotationX">1 0 0 180.0</rotate> <rotate sid="rotationY">0 1 0 0</rotate> <rotate sid="rotationZ">0 0 1 180</rotate> <scale sid="scale">0.1 0.1 0.1</scale> <!-- Equals sign #1 --> ...This model works in both visualization venues. But inside the Oculus Rift S environment, there is a considerable amount of flickering associated with the configuration's animation; it appears as though the (admittedly crude) way we have assembled a group of cubes in order to "draw" each alpha-numeric character adds a heavy burden to the 3D rendering task. (My Mac Pro's Preview app does not complain about this extra rendering burden.)
Mac Preview of … b41c385Rot08.dae b41c385Clock01.dae 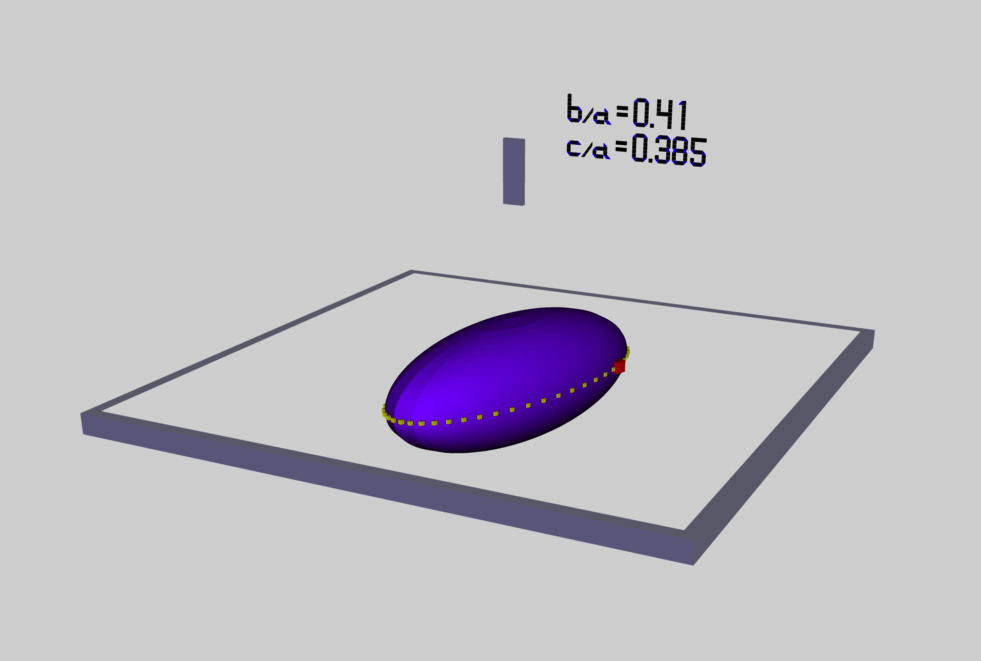
-
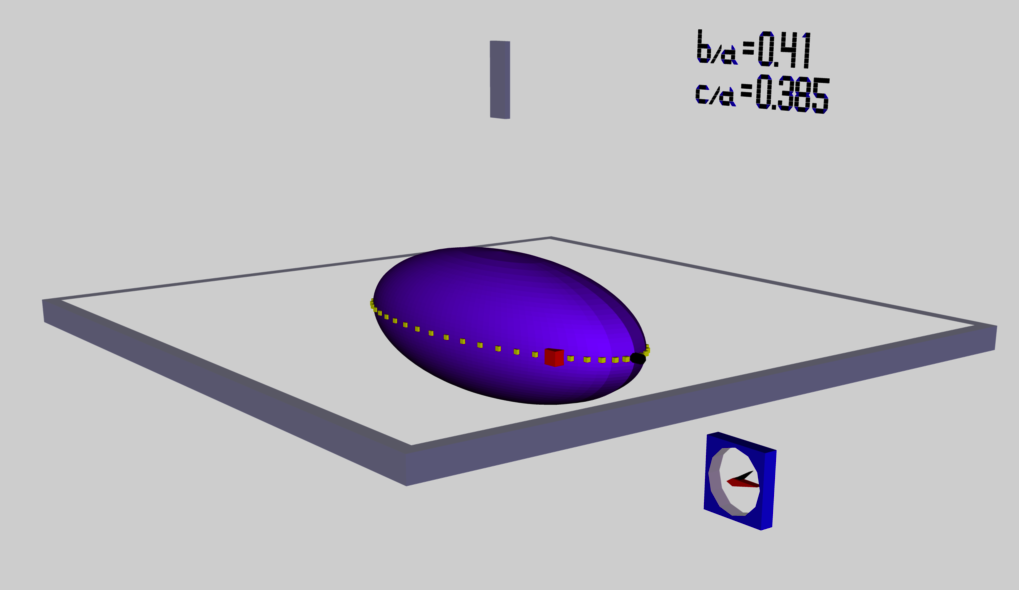
b41c385Clock01.dae (rotating frame):
We added all of the elements of a wall-clock that we had installed in our previous (prior to Oculus Rift S purchase) modeling of the b41c385 S-Type Riemann ellipsoid. As can be seen in the above image, the clock shows up below the equatorial plane, so we need to readjust its vertical location as we did with the alpha-numeric labeling. This can be altered easily.
When viewed using the Mac's Preview app, the hands on the clock appear to be turning properly, and at the desired rates. However, when viewed in the Oculus Rift S environment, the hands on the clock are sticking out of the plane that defines the clock's face, and they are spinning about a weird axis. We need to sort this out and fix it.
Fix Clock Inside Oculus Rift Environment
-
Clock06.dae:
Minute (red) hand of clock is initially oriented the correct way, but it is spinning about the wrong axis. -
Clock08.dae: (Oculus viewpoint)
Both hands start off pointing at the same number (9) on the clock — that is, they appear to start at 9:45 — and they both move in the correct plane and both appear to be moving at the correct speeds (through the dictated, 12 seconds). But the hands move in opposite directions: the minute (red) hand moves clockwise while the hour (black) hand moves counter-clockwise. -
Clock11.dae:
My aim, here, was to construct a simpler <visual_scene> that simply contains a clock frame (no hands) at the origin, and a working clock located at (x, y, z) = (7.5, 0.0, 2.0). I did this initially by creating two separate <visual_scenes>: one, still named "ID1", that contains the entire ellipsoid scene but with no clock; and a second, named "ClockPractice" that only contains the clock (plus a separate clock frame with no hands). Then inside the last set of <scene> instructions, the only specified <instance_visual_scene> was the "ClockPractice." This worked in the Mac Preview app, but the Oculus Rift S was unable to import the file. (Another case where zero debugging information was provided, so I don't really know why there was a complaint.) So … I moved on to another attempt … -
Clock12.dae:
Here, we completely deleted the large <visual_scene> named "ID1" and simply specified the one named "ClockPractice." I was able to load this file successfully into the Oculus Rift S as well as into the Mac Preview app. The Mac Preview app displayed the scene as I had envisioned it, with both hands of the clock spinning counter-clockwise — this was consistent with me specifying increasing values of the spin ANGLE. The Oculus Rift S also displayed the scene as I had envisioned it, but the two clock hands spun in opposite directions and the minute hand appeared to be spinning too slowly. -
Clock13.dae:
This model works in both visualization venues. In the previous model (Clock12.dae), I specified only the beginning TIME/ANGLE and the ending TIME/ANGLE. The Mac Preview correctly interpreted this to mean that I wanted all of the angles to increase linearly with time. But, evidently, the Oculus Rift S — or, more likely, it was the KG's converter — took the shorter route to the ending ANGLE of approximately 270°, that is, it went clockwise instead of counter-clockwise to get from the beginning ANGLE to the ending one. In this new model, we have given more explicit instructions. We have specified a total of 13 TIME values and 13 ANGLE values, so the KG's converter (or Oculus) sent both clock hands counter-clockwise, as was our intention. -
Clock14.dae:
Tried incrementing the ANGLE in the negative direction for both hands. This does not work in the Oculus Rift S venue!
WAIT!!! Maybe if we want the ANGLE to decrement, we should always start with a large value of the ANGLE, then decrease it incrementally such that it never goes negative.
Implement Decrement Idea
-
Clock16.dae:
Tried the "decrement" idea just suggested and it works in both visualization venues. Hooray! -
Decrement09.dae:
Made a copy of the above-discussed model, b41c385Rot08.dae, and renamed it "Decrement09.dae". Changed a few "translate" and "rotate" commands in order to undo the earlier attempt to create a clockwise spin in the rotating frame. These changes did result in a counter-clockwise motion, as expected, in both visualization venues. -
Decrement10.dae:
Changed only one thing: decremented the 31 ANGLE values that get <channel>ed to target "Inertial/rotationZ.ANGLE".
EXCELLENT! Works properly in both visualization venues. -
Decrement12.dae:
This model file results from inserting the clock components from Clock16.dae into the file named Decrement10.dae, which contains the Jacobi-like ellipsoidal model (with "frame"). RESULT: Works properly in both visualization venues.
There are obvious tweaks still to be inserted: (1) re-orient the clock so that it is properly mounted on the wall; and (2) explicitly enter the TIME and ANGLE values that will extend the motion of the clock hands all the way through five full "ellipsoid" rotation periods. -
Clock18.dae and Decrement24.dae:
This is 13 May 2020, and for the past couple of days I have been stuck with one unsolved problem: I am using a "decrement" approach to specifying the motion of both the minute hand and the hour hand and the motion of the HourHand appears to be correct (e.g., clockwise motion) in both visualization venues. And while the minute hand works fine when using the Mac Preview app, for some reason, the minute hand spins counter-clockwise inside the Oculus Rift S environment. I have been trying all sorts of minor code modifications in an effort to fix this (last remaining?) problem, to no avail. The most recently created versions of the two codes that exhibit this confusing behavior are, "Clock18.dae" and "Decrement24.dae"; the ".glb" version of both these codes have been successfully imported into the Oculus Rift S.
Attempts to Resolve Rotation Problem
Some restrictions imposed by glTF (presumably including the .glb binary version) are documented by the Open Game Engine Exchange (OpenGEX). For example, in the context of Animation of rotation angles,
- glTF exhibits the following MINOR PROBLEM: "All rotations must be expressed as quaternions, and slerp is required to interpolate them linearly." Note that, according to a researchgate.net discussion, "Slerp is … a shorthand for spherical linear interpolation 9".
- See also … a discussion of Animation: quaternion vs. axis-angle
- Try: <COLLADA xmlns="http://www.collada.org/2008/03/COLLADASchema" version="1.5.0">
Poking around on the web, we have found the following example COLLADA code by developer "kuchumovn" that uses a quaternion prescription to animate about the Z-axis.
<library_animations>
<animation id="animation">
<source id="timing">
<float-array id="timing_array" count="2">
0.0 1.0
</float-array>
<technique_common>
<accessor source="#timing_array" count="2" stride="1">
<param name="TIME" type="float"/>
</accessor>
</technique_common>
</source>
<source id="transformations">
<float_array id="transformations_array" count="32">
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
2 0 0 0 0 2 0 0 0 0 2 0 0 0 0 2
</float_array>
<technique_common>
<accessor source="#transformations_array" count="2" stride="16">
<param name="(0)(0)" type="float4x4"/>
</accessor>
</technique_common>
</source>
<source id="interpolations">
<Name_array id="interpolations_array" count="2">LINEAR LINEAR</Name_array>
<technique_common>
<accessor source="#interpolations_array" count="2" stride="1">
<param name="INTERPOLATION" type="Name"/>
</accessor>
</technique_common>
</source>
<sampler id="sampler">
<input semantic="INPUT" source="#timing"/>
<input semantic="OUTPUT" source="#transformations"/>
<input semantic="INTERPOLATION" source="#interpolations"/>
</sampler>
<channel source="#sampler" target="#3d-object-node/transformation"/>
</animation>
</library_animations>
// scene
<library_visual_scenes>
<visual_scene id="scene" name="scene">
<node id="3d-object-node" name="3d-object-node" type="NODE">
<matrix sid="transformation">1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1</matrix>
<instance_geometry> ... </instance_geometry>
</node>
</visual_scene>
</library_visual_scenes>
From our accompanying introductory discussion of the COLLADA Position Matrix, we recognize that if we allow for scaling and translation along with rotation only about the Z-axis, the relevant 4×4 matrix is,
|
= |
|
||||||||||||||||||||||||||
and the equivalent <matrix> instruction should be (ignore the square brackets around each term),
| <matrix>[ Sx · cos(γ) ] [ -Sx · sin(γ) ] [ 0 ] [ Tx] [ Sy · sin(γ) ] [ Sy · cos(γ) ] [ 0 ] [ Ty] [ 0 ] [ 0 ] [ Sz] [ Tz] [ 0 ] [ 0 ] [ 0 ] [ 1 ]</matrix> . |
-
WorksClock22E.dae (originally, "Clock22E.dae"):
This appears to work in both visualization venues. Hooray! -
WorksQuaternion30.dae (originally, "quaternion30.dae"):
This appears to work in both visualization venues. Hooray!
Building on the advice/suggestion drawn from the "kuchumovn" COLLADA-code segment, above, we have figured out how to assemble a quaternion-based representation of a Z-rotation that works both in the Mac's Preview app and in the environment of the Oculus Rift S. Here are some key lines of code that appear in our model file named, WorksQuaternion30.dae …
<animation id="Cube_quaternion_Z">
<source id="Cube_quaternion_Z-input">
<float_array id="Cube_quaternion_Z-input-array" count=" 33">
0.00
0.25
0.50
0.75
1.00
1.25
1.50
1.75
2.00
2.25
2.50
2.75
3.00
3.25
3.50
3.75
4.00
4.25
4.50
4.75
5.00
5.25
5.50
5.75
6.00
6.25
6.50
6.75
7.00
7.25
7.50
7.75
8.00
</float_array>
<technique_common>
<accessor source="#Cube_quaternion_Z-input-array" count=" 33" stride="1">
<param name="TIME" type="float"/>
</accessor>
</technique_common>
</source>
<source id="Cube_quaternion_Z-output">
<float_array id="Cube_quaternion_Z-output-array" count="528">
0.000 1.000 0.000 7.500 -1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.383 0.924 0.000 7.500 -0.924 -0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.707 0.707 0.000 7.500 -0.707 -0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.924 0.383 0.000 7.500 -0.383 -0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-1.000 0.000 0.000 7.500 0.000 -1.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.924 -0.383 0.000 7.500 0.383 -0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.707 -0.707 0.000 7.500 0.707 -0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.383 -0.924 0.000 7.500 0.924 -0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.000 -1.000 0.000 7.500 1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.383 -0.924 0.000 7.500 0.924 0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.707 -0.707 0.000 7.500 0.707 0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.924 -0.383 0.000 7.500 0.383 0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
1.000 0.000 0.000 7.500 0.000 1.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.924 0.383 0.000 7.500 -0.383 0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.707 0.707 0.000 7.500 -0.707 0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.383 0.924 0.000 7.500 -0.924 0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.000 1.000 0.000 7.500 -1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.383 0.924 0.000 7.500 -0.924 -0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.707 0.707 0.000 7.500 -0.707 -0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.924 0.383 0.000 7.500 -0.383 -0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-1.000 0.000 0.000 7.500 0.000 -1.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.924 -0.383 0.000 7.500 0.383 -0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.707 -0.707 0.000 7.500 0.707 -0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
-0.383 -0.924 0.000 7.500 0.924 -0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.000 -1.000 0.000 7.500 1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.383 -0.924 0.000 7.500 0.924 0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.707 -0.707 0.000 7.500 0.707 0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.924 -0.383 0.000 7.500 0.383 0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
1.000 0.000 0.000 7.500 0.000 1.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.924 0.383 0.000 7.500 -0.383 0.924 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.707 0.707 0.000 7.500 -0.707 0.707 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.383 0.924 0.000 7.500 -0.924 0.383 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
0.000 1.000 0.000 7.500 -1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000
</float_array>
<technique_common>
<accessor source="#Cube_quaternion_Z-output-array" count=" 33" stride="16">
<param name="TRANSFORM" type="float4x4"/>
</accessor>
</technique_common>
</source>
<sampler id="Cube_quaternion_Z-sampler">
<input semantic="INPUT" source="#Cube_quaternion_Z-input"/>
<input semantic="OUTPUT" source="#Cube_quaternion_Z-output"/>
</sampler>
<channel source="#Cube_quaternion_Z-sampler" target="Jetman/transformation"/>
</animation>
....
<library_visual_scenes>
<visual_scene id="ID1">
....
<!-- END LABELING HERE -->
</node>
</node> <!-- End Inertial Grouping of Objects -->
<!-- BEGIN CLOCK -->
<node id="firstclock" name="instance_1"> <!-- TWO -->
<translate>7.5 0.0 2.0</translate>
<rotate sid="rotationX">0.0 1.0 0.0 0.0</rotate>
<rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate>
<rotate sid="rotationZ">0.0 0.0 1.0 0.0</rotate>
<scale sid="scale">1.0 1.0 1.0</scale>
<instance_node url="#ID3" />
</node> <!-- /TWO -->
<node id="Jetman" name="instance_Arrow"> <!-- TWO -->
<matrix sid="transformation"> 0.000 1.000 0.000 7.500 -1.000 0.000 0.000 0.000 0.000 0.000 1.000 2.000 0.000 0.000 0.000 1.000</matrix>
<instance_node url="#ArrowID3" />
</node> <!-- /TWO -->
<node id="HourHand" name="instance_Hour"> <!-- TWO -->
<translate>7.5 0.0 2.0</translate>
<rotate sid="rotationX">0.0 1.0 0.0 0.0</rotate>
<rotate sid="rotationY">0.0 1.0 0.0 0.0</rotate>
<rotate sid="rotationZ">0.0 0.0 1 270.0</rotate>
<scale sid="scale">0.75 0.75 0.75</scale>
<instance_node url="#HourID3" />
</node> <!-- /TWO -->
<!-- END CLOCK -->
</visual_scene>
</library_visual_scenes>
Final Touches
What I really need to do in order to properly mount the clock on a vertical wall is to rotate it permanently by -90° about the Y-axis before rotating it in a time-varying way about the Z-axis. In this situation, the relevant 4×4 matrix is,
|
= |
|
||||||||||||||||||||||||||
and the equivalent <matrix> instruction should be (ignore the square brackets around each term),
| <matrix>[ 0 ] [ 0 ] [ -Sx ] [ Tx ] [ Sy · sin(γ) ] [ Sy · cos(γ) ] [ 0 ] [ Ty ] [ Sz · cos(γ) ] [ -Sz · sin(γ) ] [ 0] [ Tz ] [ 0 ] [ 0 ] [ 0 ] [ 1 ]</matrix> . |
-
Final09.dae:
In this model, the clock is neatly mounted on the "wall" next to the alpha-numeric labeling; the scene is being displayed from the rotating frame of reference; the minute-hand runs through 5.0 compete cycles, but the hour hand stops after 2.0 cycles. This appears to work in both visualization venues.
Here are some remaining details that need to be completed:- In order for the system to complete 5.000 spins of the ellipsoid, the minute hand needs to keep turning through 1.8252 × 5 = 9.1260 cycles; since we want each clock cycle to take 4.000 seconds of TIME, this means that TIME_max = 36.5040 seconds.
- Carry the "hour hand" through 9.1260 hours; it should run up through the same TIME_max, but spin 1/12 as fast as the minute hand.
- Create an inertial-frame visual_scene.
- Consider constructing the alpha-numeric "objects" a more efficient way so that, inside the Oculus Rift S environment, the animation is much smoother.
- In the rotating frame model, make the purple ellipsoid somewhat transparent to reveal the internal trajectories of various Lagrange particles, not just the single red particle that now moves in the equatorial plane along the ellipsoid surface.
-
Final15.dae:
Cleaned up a number of scaling issues. For example, in the above-discussed quaternion <matrix>, we have set Tx = Ty = Tz = 0.0, and we have set Sx = Sy = Sz = 1.0. This way, the quaternion <matrix> arrays handle only the Euler-angle specifications while all of the translations and scalings are specified in overarching "parent" nodes. This works in both visualization venues. -
Final17.dae TERRIFIC !:
Both hands of the clock now continue to cycle smoothly (through 9.126 "hours" = 9h 8m) while the laboratory frame completes 5.0 full spin periods — which will be 5.0 full spins of the ellipsoid as viewed from the inertial frame. This works in both visualization venues. -
Inertial17.dae:
This is identical to "Final17.dae" except that the system is viewed from the inertial frame of reference. This works in both visualization venues.
Multiple Lagrangian Fluid Elements
-
MultiLagrange18.dae:
The basic elements of this model are identical to the one, above, named "Final17.dae", but we have modified it to complete the 5th remaining detail enumerated above. Specifically, in this rotating frame model, we have made the purple ellipsoid somewhat transparent to reveal the internal trajectories of three Lagrange particles. This works in both visualization venues! -
MultiLagrange20.dae:
In this model, we show the motion of six Lagrange particles. This works in both visualization venues! -
MultiLagrange21.dae:
Make all six of the Lagrangian "red cube" markers smaller.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |