Difference between revisions of "User:Tohline/Appendix/Ramblings/Dyson1893Part1"
| Line 48: | Line 48: | ||
</table> | </table> | ||
where (see beginning of §8 on p. 61), | where (see beginning of §8 on p. 61), | ||
<table border="0" cellpadding="10" align="right" width="35%"><tr><td align="center"> | |||
<table border="0" cellpadding="5" align="right" width="100%"> | |||
<tr> | |||
<td align="center"> | |||
[[File:DysonTorusIllustration03.png|300px|center|Anchor Ring Schematic]]<br /> | |||
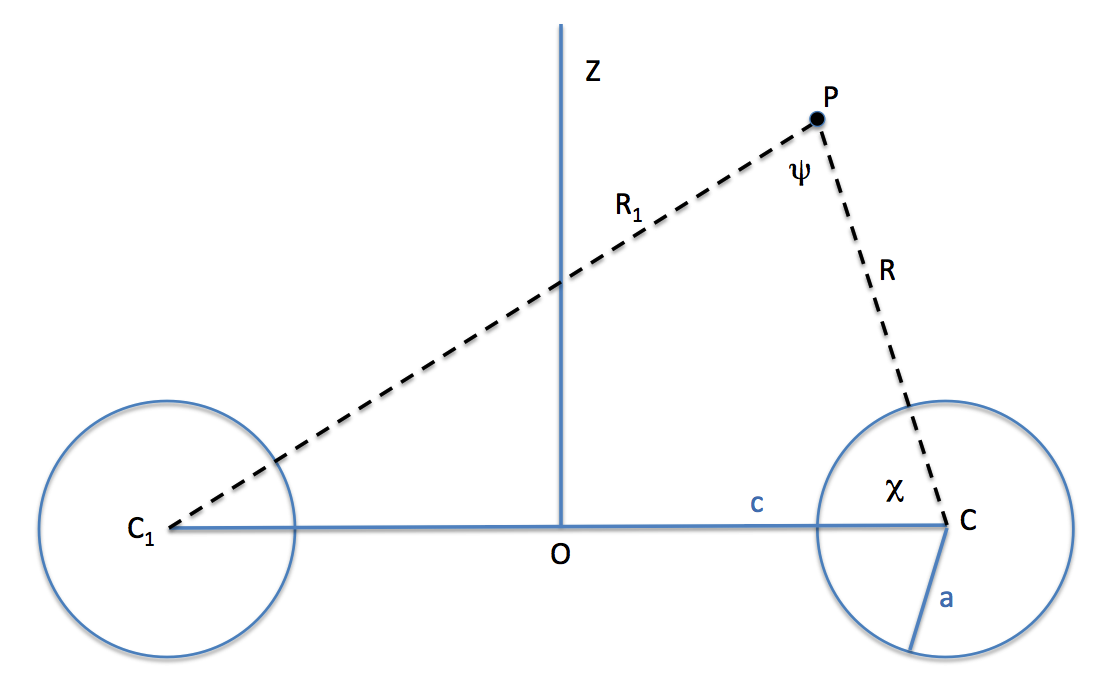
'''Caption:''' [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm Anchor ring] schematic, adapted from figure near the top of §2 (on p. 47) of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)] | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 289: | Line 298: | ||
</tr> | </tr> | ||
</table> | </table> | ||
This is the expression for <math>~\mathfrak{I}(r,\theta,c) </math> that was adopted by Dyson at the beginning of his §8. Subsequently, Dyson was able to obtain analytic expressions for successive derivatives of the function, <math>~\mathfrak{I}(r,\theta,c) </math>, by first demonstrating that | This is the expression for <math>~\mathfrak{I}(r,\theta,c) </math> that was adopted by Dyson at the beginning of his §8. Subsequently, Dyson was able to obtain analytic expressions for successive derivatives of the function, <math>~\mathfrak{I}(r,\theta,c) </math>, by first demonstrating that | ||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{dR}{dc}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4c^2 + R^2 - R_1^2}{4cR} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{dR_1}{dc}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4c^2 + R_1^2 - R^2}{4cR} \, ,</math> and, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\mu}{dc}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\mu}{c} \cos\psi \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where — as shown above in the [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm Anchor ring] schematic — <math>~\psi</math> is the angle between <math>~R</math> and <math>~R_1</math>. | |||
<table border="1" align="center" cellpadding="8" width="70%"> | <table border="1" align="center" cellpadding="8" width="70%"> | ||
<tr> | <tr> | ||
| Line 384: | Line 431: | ||
</table> | </table> | ||
Then, drawing upon known expressions for the derivatives of elliptic integrals, as are now tidily catalogued online in [http://dlmf.nist.gov/ NIST's ''Digital Library of Mathematical Functions''], Dyson showed that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\mathfrak{I}(r,\theta,c)}{dc} = \frac{d}{dc}\biggl[\frac{4K(\mu)}{R_1+R}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
4K(\mu) \frac{d}{dc}\biggl[ R_1 + R \biggr]^{-1} | |||
+ | |||
\frac{4}{(R_1+R)} \biggl[ \frac{E\left(\mu\right)-{\mu^{\prime}}^{2}K\left(\mu\right)}{\mu{\mu^{\prime}}^{2}} \biggr]\frac{d\mu}{dc} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{c}\biggl\{\frac{E(\mu)(R+R_1)}{RR_1} \cdot \cos\psi ~-~\frac{4K(\mu)}{R+R_1} \cdot \cos^2\frac{\psi}{2} \biggr\} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Revision as of 21:47, 17 September 2018
Dyson (1893a) Part I: Some Details
This chapter provides some derivation details relevant to our accompanying discussion of Dyson's analysis of the gravitational potential exterior to an anchor ring.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Overview
In his pioneering work, F. W. Dyson (1893a, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893b, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.
External Potential
On p. 59, at the end of §6 of Dyson (1893a), we find the following expression for the potential at point "P", anywhere exterior to an anchor ring:
|
<math>~\frac{\pi V(r,\theta)}{M}</math> |
<math>~=</math> |
<math>~ \mathfrak{I}(r,\theta,c) ~+~ \frac{1}{2^3}\biggl(\frac{a^2}{c}\biggr) \frac{d}{dc} \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~-~ \frac{1}{2^6\cdot 3}\biggl(\frac{a^2}{c}\biggr)^2 \frac{d^2}{dc^2} \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~+~\cdots </math> |
|
|
|
<math>~ ~+~(-1)^{n+1} \frac{2}{2n+2} \biggl[ \frac{1\cdot 3\cdot 5 \cdots (2n-3)}{2^2\cdot 4^2\cdot 6^2\cdots(2n)^2} \biggr] \biggl(\frac{a^2}{c}\biggr)^n \frac{d^n}{dc^n} \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~+~ \cdots </math> |
where (see beginning of §8 on p. 61),
|
|
<math>~\mathfrak{I}(r,\theta,c)</math> |
<math>~\equiv</math> |
<math>~ \int_0^\pi d\phi \biggl[r^2 - 2cr\sin\theta \cos\phi +c^2\biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ 2\int_0^{\pi/2} d\phi \biggl[ R_1^2 - (R_1^2-R^2)\sin^2\phi \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2}{R_1}\int_0^{\pi/2} d\phi \biggl[ 1 - \biggl( \frac{R_1^2-R^2}{R_1^2}\biggr) \sin^2\phi \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(k)}{R_1} \, , </math> |
and, where furthermore,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ \int_0^{\pi/2} d\phi \biggl[1 - k^2\sin^2\phi \bigg]^{-1 / 2} </math> |
and |
<math>~k</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{R_1^2-R^2}{R_1^2} \biggr]^{1 / 2} \, . </math> |
Taking a queue from our accompanying discussion of toroidal coordinates, if we adopt the variable notation,
<math>~\eta \equiv \ln\biggl(\frac{R_1}{R}\biggr) \, ,</math>
then we can write,
|
<math>~\cosh\eta = \frac{1}{2}\biggl[e^\eta + e^{-\eta}\biggr]</math> |
<math>~=</math> |
<math>~\frac{R^2 + R_1^2}{2RR_1} \, ,</math> |
which implies that,
|
<math>~\biggl[ \frac{2}{\coth\eta +1} \biggr]^{1 / 2} = [1 - e^{-2\eta}]^{1 / 2}</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \biggl(\frac{R}{R_1}\biggr)^2 \biggr]^{1 / 2} = k \, .</math> |
Now, if we employ the Descending Landen Transformation for the complete elliptic integral of the first kind, we can make the substitution,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ (1 + \mu)K(\mu) \, , </math> |
where, |
<math>~\mu</math> |
<math>~\equiv</math> |
<math>~ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} \, . </math> |
But notice that, <math>~\sqrt{1-k^2} = e^{-\eta}</math>, in which case,
|
<math>~\mu </math> |
<math>~=</math> |
<math>~ \frac{1-e^{-\eta}}{1+e^{-\eta}} </math> |
<math>~=</math> |
<math>~ \frac{1-R/R_1}{1+R/R_1} </math> |
<math>~=</math> |
<math>~ \frac{R_1-R}{R_1+R} \, . </math> |
Hence, we can write,
|
<math>~\mathfrak{I}(r,\theta,c) = \frac{2K(k)}{R_1}</math> |
<math>~=</math> |
<math>~ \frac{2}{R_1} \biggl[(1+\mu)K(\mu) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{2K(\mu)}{R_1} \biggl[1+\frac{R_1-R}{R_1+R} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{4K(\mu)}{R_1+R} \, .</math> |
This is the expression for <math>~\mathfrak{I}(r,\theta,c) </math> that was adopted by Dyson at the beginning of his §8. Subsequently, Dyson was able to obtain analytic expressions for successive derivatives of the function, <math>~\mathfrak{I}(r,\theta,c) </math>, by first demonstrating that
|
<math>~\frac{dR}{dc}</math> |
<math>~=</math> |
<math>~\frac{4c^2 + R^2 - R_1^2}{4cR} \, ,</math> |
|
<math>~\frac{dR_1}{dc}</math> |
<math>~=</math> |
<math>~\frac{4c^2 + R_1^2 - R^2}{4cR} \, ,</math> and, |
|
<math>~\frac{d\mu}{dc}</math> |
<math>~=</math> |
<math>~\frac{\mu}{c} \cos\psi \, ,</math> |
where — as shown above in the Anchor ring schematic — <math>~\psi</math> is the angle between <math>~R</math> and <math>~R_1</math>.
|
LaTeX mathematical expressions cut-and-pasted directly from
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
According to §19.4 of NIST's Digital Library of Mathematical Functions,
where, <math>~k^{\prime} \equiv \sqrt{1 - k^2} \, .</math> |
Then, drawing upon known expressions for the derivatives of elliptic integrals, as are now tidily catalogued online in NIST's Digital Library of Mathematical Functions, Dyson showed that,
|
<math>~\frac{d\mathfrak{I}(r,\theta,c)}{dc} = \frac{d}{dc}\biggl[\frac{4K(\mu)}{R_1+R}\biggr]</math> |
<math>~=</math> |
<math>~ 4K(\mu) \frac{d}{dc}\biggl[ R_1 + R \biggr]^{-1} + \frac{4}{(R_1+R)} \biggl[ \frac{E\left(\mu\right)-{\mu^{\prime}}^{2}K\left(\mu\right)}{\mu{\mu^{\prime}}^{2}} \biggr]\frac{d\mu}{dc} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c}\biggl\{\frac{E(\mu)(R+R_1)}{RR_1} \cdot \cos\psi ~-~\frac{4K(\mu)}{R+R_1} \cdot \cos^2\frac{\psi}{2} \biggr\} \, ; </math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |