Difference between revisions of "User:Tohline/Appendix/Ramblings/BordeauxSequences"
| Line 70: | Line 70: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
[[File: | [[File:AKM2003Fig2.png|center|800px|Figure 2 from Ansorg, Kleinwächter & Meinel (2003)]] | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="left"> | <td align="left"> | ||
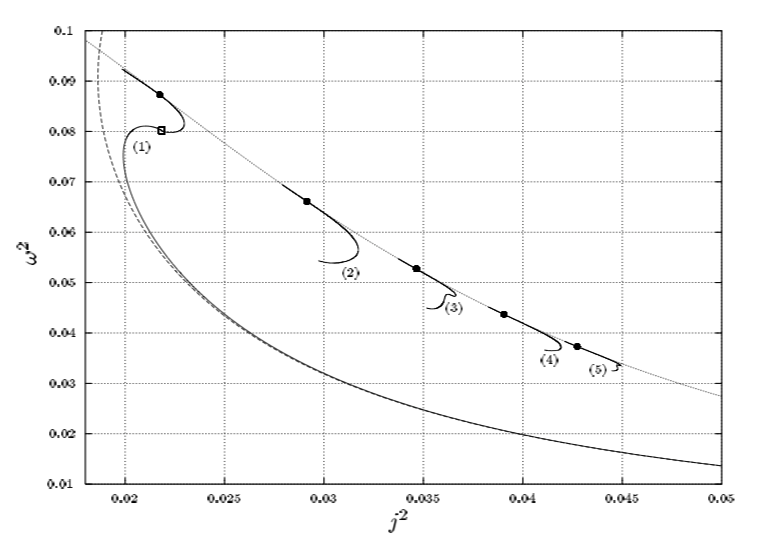
CAPTION: | CAPTION: For the first five axisymmetric sequences, <math>~\omega_0^2</math> is plotted against the dimensionless squared angular momentum, <math>~j^2</math>, using the same normalizations as Eriguchi & Hachisu (1983). Dotted and dashed curves again refer to the Maclaurin sequence and the Dyson approximation respectively. The full circles mark the bifurcation points on the Maclaurin sequence, and the open square the transition configuration of spheroidal to toroidal bodies on the Dyson ring sequence. | ||
< | |||
< | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 23:40, 29 July 2020
Université de Bordeaux (Part 2)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Exterior Gravitational Potential of Toroids
J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.
We discuss this topic in a separate, accompanying chapter.
Spheroid-Ring Systems
Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.
Key References
Here are some relevant publications:
- Hachisu (1986a, ApJS, 61, 479): A Versatile Method for Obtaining Structures of Rapidly Rotating Stars
- Fujisawa & Eriguchi (2014, MNRAS, 438, L61): Prolate stars due to meridional flows
- Huré, Hersant & Nasello (2018, MNRAS, 475, 63): The equilibrium of overpressurized polytropes
- & Eriguchi (1984, Ap&SS, 99, 71): Fission Sequence and Equilibrium Models of [Rigidly] Rotating Polytropes
- Hachisu, Eriguchi & Nomoto (1986b, ApJ, 311, 214): Fate of merging double white dwarfs. II - Numerical method
- Nishida, Eriguchi & Lanza (1992, ApJ, 401, 618): General Relativistic Structure of Star-Toroid Systems
- Woodward, Sankaran & Tohline (1992 ApJ, 394, 248): Tidal Disruption of a Star by a Massive Disk (The Axisymmetric Roche Problem)
Especially,
- Eriguchi & Hachisu (1983, Prog. Theor. Phys., 69, 1131): Two Kinds of Axially Symmetric Equilibrium Sequences of Self-Gravitating and Rotating Incompressible Fluids: Two-Ring Sequence and Core-Ring Sequence
- Ansorg, Kleinwächter & Meinel (2003, MNRAS, 339, 515): Uniformly rotating axisymmetric fluid configurations bifurcating from highly flattened Maclaurin spheroids
- Hachisu, Eriguchi & Nomoto (1986a, ApJ, 308, 161): Fate of Merging Double White Dwarfs
Key Figures
Eriguchi & Hachisu (1983)
|
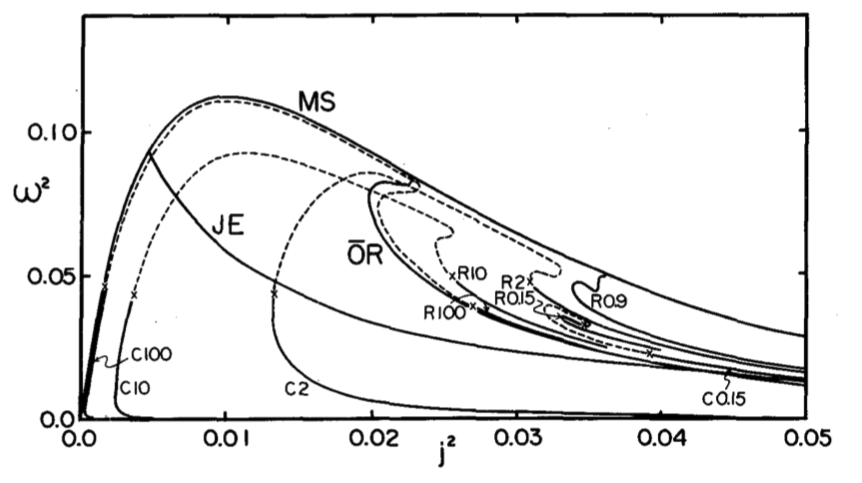
Fig. 3 extracted without modification from p. 1134 of Eriguchi & Hachisu (1983)
"Two Kinds of Axially Symmetric Equilibrium Sequences of Self-Gravitating and Rotating Incompressible Fluids: Two-Ring Sequence and Core-Ring Sequence" Progress of Theoretical Physics, vol. 69, pp. 1131-1136 © Progress of Theoretical Physics |
|
CAPTION: The angular momentum-angular velocity relations. Solid curves represent uniformly rotating equilibrium sequences.
The number and letter R or C attached to a curve denote mass ratio and two-ring or core-ring sequence, respectively. If differential rotation is allowed, the equilibrium sequences may continue to exist as shown by the dashed curves. |
AKM (2003)
|
Fig. 2 extracted without modification from p. 517 of Ansorg, Kleinwächter & Meinel (2003)
"Uniformly rotating axisymmetric fluid configurations bifurcating from highly flattened Maclaurin spheroids"
MNRAS, vol. 339, pp. 515-523 © Royal Astronomical Society |
|
CAPTION: For the first five axisymmetric sequences, <math>~\omega_0^2</math> is plotted against the dimensionless squared angular momentum, <math>~j^2</math>, using the same normalizations as Eriguchi & Hachisu (1983). Dotted and dashed curves again refer to the Maclaurin sequence and the Dyson approximation respectively. The full circles mark the bifurcation points on the Maclaurin sequence, and the open square the transition configuration of spheroidal to toroidal bodies on the Dyson ring sequence. |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |