VisTrails Home

User:Tohline/Appendix/Ramblings/BordeauxSequences

From VisTrailsWiki

(Difference between revisions)
Jump to: navigation, search
(→Key Figures)
(→Basillais & Huré (2019))
Line 123: Line 123:
</tr>
</tr>
</table>
</table>
 +
 +
 +
Let's examine the "high-&omega; limit" that has been ''fit'' by their equation (3), noting that <math>~\omega^2</math> and <math>~\rho</math> are uniform throughout each two-component, equilibrium configuration.  We expect each (thin) ring component to be spinning with the Keplerian frequency,
 +
<table border="0" cellpadding="5" align="center">
 +
 +
<tr>
 +
  <td align="right">
 +
<math>~\frac{r^2 \omega^2_\mathrm{K} }{r}</math>
 +
  </td>
 +
  <td align="center">
 +
<math>~=</math>
 +
  </td>
 +
  <td align="left">
 +
<math>~\frac{GM_\mathrm{pt}}{r^2}</math>
 +
  </td>
 +
</tr>
 +
 +
<tr>
 +
  <td align="right">
 +
<math>~\Rightarrow ~~~ \omega_K^2</math>
 +
  </td>
 +
  <td align="center">
 +
<math>~=</math>
 +
  </td>
 +
  <td align="left">
 +
<math>~\frac{GM_\mathrm{pt}}{r^3}
 +
=
 +
\biggl(\frac{G}{r^3}\biggr) \frac{4\pi {\bar{a}}^3 \rho}{3}
 +
</math>
 +
  </td>
 +
</tr>
 +
 +
<tr>
 +
  <td align="right">
 +
<math>~\Rightarrow ~~~\frac{ \omega_K^2}{4\pi G\rho}</math>
 +
  </td>
 +
  <td align="center">
 +
<math>~=</math>
 +
  </td>
 +
  <td align="left">
 +
<math>~
 +
\biggl(\frac{{\bar{a}}^3}{3r^3}\biggr) \, .
 +
</math>
 +
  </td>
 +
</tr>
 +
</table>
 +
{{LSU_HBook_footer}}
{{LSU_HBook_footer}}

Revision as of 18:48, 21 November 2020

Contents

Université de Bordeaux (Part 2)

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Exterior Gravitational Potential of Toroids

J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.

We discuss this topic in a separate, accompanying chapter.

Spheroid-Ring Systems

Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.

Key References

Here are some relevant publications:

Especially,

Key Figures

Eriguchi & Sugimoto (1981)

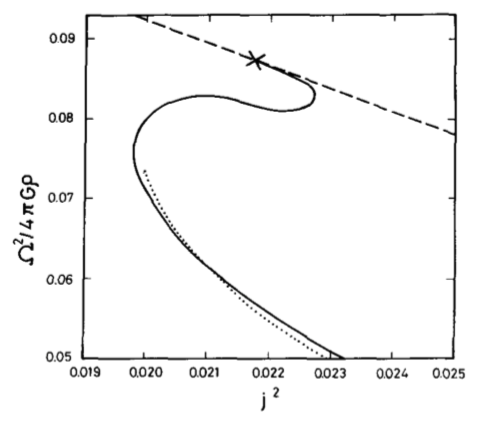
Fig. 1 extracted without modification from p. 1873 of Eriguchi & Sugimoto (1981)

"Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid"

Progress of Theoretical Physics,

vol. 65, pp. 1870-1875 © Progress of Theoretical Physics

Figure 3 from Eriguchi & Hachisu (1983)

CAPTION (modified here):   The squared angular velocity is plotted against ~j^2 for a segment of the Maclaurin sequence (dashed curve), for the Dyson-Wong sequence (dotted curve), and for the new configurations reported in this 1981 paper by Eriguchi & Sugimoto (solid curve). The "×" mark denotes the neutral point on the Maclaurin sequence against the ~P_4(\eta) perturbation. The dotted curve is plotted by using the values which are read from the curve of Fig. 6 of Wong (1974), so it may contain errors to some extent.


Eriguchi & Hachisu (1983)

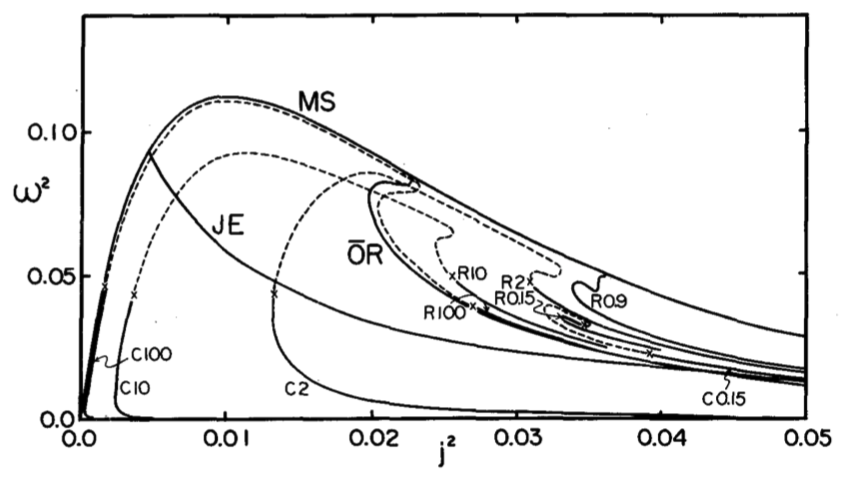
Fig. 3 extracted without modification from p. 1134 of Eriguchi & Hachisu (1983)

"Two Kinds of Axially Symmetric Equilibrium Sequences of Self-Gravitating and Rotating Incompressible Fluids:
Two-Ring Sequence and Core-Ring Sequence"

Progress of Theoretical Physics,

vol. 69, pp. 1131-1136 © Progress of Theoretical Physics

Figure 3 from Eriguchi & Hachisu (1983)

CAPTION:  The angular momentum-angular velocity relations. Solid curves represent uniformly rotating equilibrium sequences.

  • MS:   Maclaurin spheroid sequence
  • JE:   Jacobi ellipsoid sequence
  • OR:   one-ring sequence

The number and letter R or C attached to a curve denote mass ratio and two-ring or core-ring sequence, respectively. If differential rotation is allowed, the equilibrium sequences may continue to exist as shown by the dashed curves.

AKM (2003)

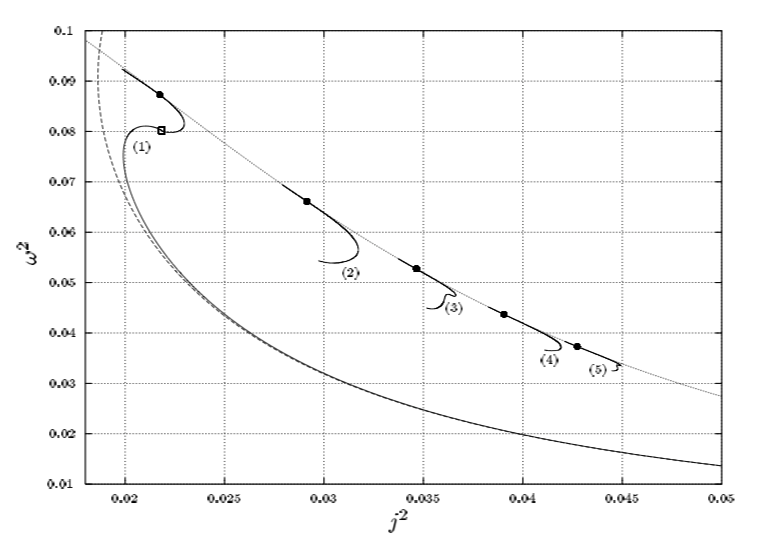
Fig. 2 extracted without modification from p. 517 of Ansorg, Kleinwächter & Meinel (2003)

"Uniformly rotating axisymmetric fluid configurations bifurcating from highly flattened Maclaurin spheroids"

MNRAS, vol. 339, pp. 515-523 © Royal Astronomical Society

Figure 2 from Ansorg, Kleinwächter & Meinel (2003)

CAPTION:   For the first five axisymmetric sequences, ~\omega_0^2 is plotted against the dimensionless squared angular momentum, ~j^2, using the same normalizations as Eriguchi & Hachisu (1983). Dotted and dashed curves again refer to the Maclaurin sequence and the Dyson approximation respectively. The full circles mark the bifurcation points on the Maclaurin sequence, and the open square the transition configuration of spheroidal to toroidal bodies on the Dyson ring sequence.

Basillais & Huré (2019)

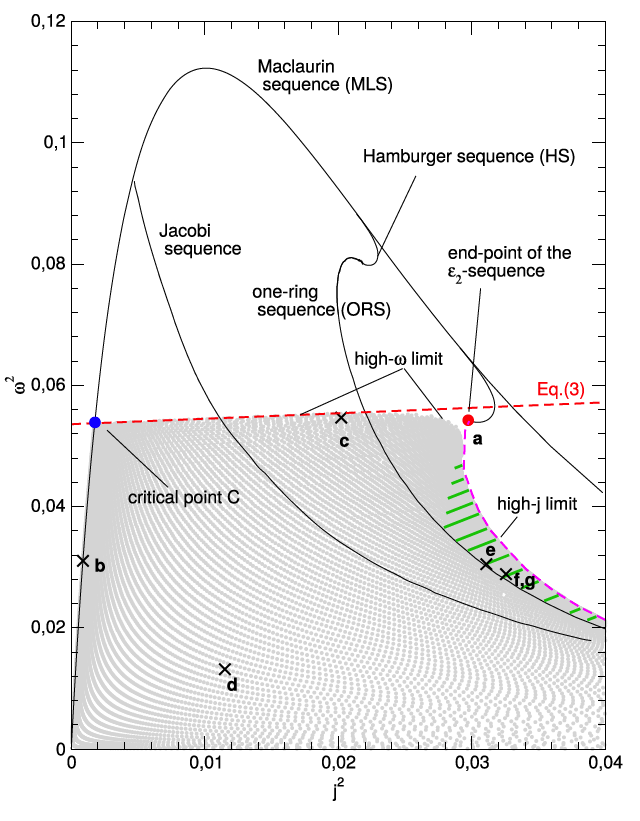
Fig. 4 extracted without modification from p. 4507 of Basillais & Huré (2019)

"Rigidly rotating, incompressible spheroid-ring systems:   new bifurcations, critical rotations, and degenerate states"

MNRAS, vol. 487, pp. 4504-4509 © Royal Astronomical Society

Figure 4 from Basillais & Huré (2019)

CAPTION:   The spheroid-ring solutions (grey dots) populate the ~\omega_0^2 - j^2 diagram in between the MLS, the high-ω limit, and the high-j limit. The MLS, ORS, Jacobi sequence, Hamburger sequence, and ε2-sequence are also shown (plain lines). Points labelled a to f (cross) correspond to equilibria shown in Figure 3; see also Table 1. There is a band of degeneracy rightward to the ORS (green dashed zone).


Let's examine the "high-ω limit" that has been fit by their equation (3), noting that ~\omega^2 and ~\rho are uniform throughout each two-component, equilibrium configuration. We expect each (thin) ring component to be spinning with the Keplerian frequency,

~\frac{r^2 \omega^2_\mathrm{K} }{r}

~=

~\frac{GM_\mathrm{pt}}{r^2}

~\Rightarrow ~~~ \omega_K^2

~=

~\frac{GM_\mathrm{pt}}{r^3} = \biggl(\frac{G}{r^3}\biggr) \frac{4\pi {\bar{a}}^3 \rho}{3}

~\Rightarrow ~~~\frac{ \omega_K^2}{4\pi G\rho}

~=

~ \biggl(\frac{{\bar{a}}^3}{3r^3}\biggr) \, .


Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2020 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |

Retrieved from "https://www.vistrails.org/index.php/User:Tohline/Appendix/Ramblings/BordeauxSequences"
Personal tools