Difference between revisions of "User:Tohline/Appendix/Ramblings/Bordeaux"
| Line 1,494: | Line 1,494: | ||
+ 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 | + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 | ||
+ 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) | + 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) | ||
\biggr\} | \biggr\} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~2[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,509: | Line 1,513: | ||
<math>~ | <math>~ | ||
z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} | z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} | ||
-~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0) | -~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0) | ||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ | |||
k_0[19z^2 - 3 ] | |||
+ 5(z-1) [2(z+1)]^{1 / 2} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 2^{5 / 2}[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
zk_0(z-1) \cdot K(k_0)\cdot K(k_0) \biggl\{ k_0 [2(z+1) ]^{1 / 2} - 5 \biggr\} | |||
-~20 z[2(z+1)]^{1 / 2} \cdot E(k_0)\cdot E(k_0) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,525: | Line 1,560: | ||
<math>~ | <math>~ | ||
+~K(k_0)\cdot E(k_0) \biggl\{ | +~K(k_0)\cdot E(k_0) \biggl\{ | ||
k_0[19z^2 - 3 ] | |||
+ 5(z-1) [2(z+1)]^{1 / 2} | |||
+ 5 | \biggr\} \, . | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
Revision as of 22:57, 26 June 2020
Université de Bordeaux

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Spheroid-Ring Systems
Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.
Exterior Gravitational Potential of Toroids
J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.
Their Presentation
On an initial reading, it appears as though the most relevant section of the Huré, et al. (2020) paper is §8 titled, The Solid Torus. They write the gravitational potential in terms of the series expansion,
|
<math>~\Psi_\mathrm{grav}(\vec{r})</math> |
<math>~\approx</math> |
<math>~ \Psi_0 + \sum\limits_{n=1}^N \Psi_n \, , </math> |
Huré, et al. (2020), §7, p. 5831, Eq. (42)
where, after setting <math>~M_\mathrm{tot} = 2\pi^2\rho_0 b^2 R_c </math> and acknowledging that <math>~V_{0,0} = 1 \, ,</math> we can write,
|
<math>~\Psi_0 </math> |
<math>~=</math> |
<math>~ - \frac{GM_\mathrm{tot}}{r} \biggl[ \frac{r}{\Delta_0} \cdot \frac{2}{\pi} \boldsymbol{K}(k_0) \biggr] </math> |
Huré, et al. (2020), §8, p. 5832, Eqs. (52) & (53)
and,
|
<math>~\frac{1}{e^2} \biggl[ \Psi_1 + \Psi_2 \biggr]</math> |
<math>~=</math> |
<math>~ - \frac{G\pi \rho_0 R_c b^2}{4 (k')^2 \Delta_0^3} \biggl\{ [\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k) - (k')^2 \Delta_0^2 \boldsymbol{K}(k) \biggr\} \, . </math> |
Huré, et al. (2020), §8, p. 5832, Eq. (54)
Note that the argument of the elliptic integral functions is,
|
<math>~k</math> |
<math>~\equiv</math> |
<math>~ \frac{2\sqrt{\varpi R}}{\Delta} </math> |
where, |
<math>~\Delta</math> |
<math>~\equiv</math> |
<math>~ \biggl[ (R + \varpi)^2 + (Z-z)^2 \biggr]^{1 / 2} \, . </math> |
Huré, et al. (2020), §2, p. 5826, Eqs. (4) & (5)
Our Presentation of Wong's (1973) Result
Setup
From our accompanying discussion of Wong's (1973) derivation, the exterior potential is given by the expression,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~\sum_{n=0}^{\mathrm{nmax}} \epsilon_n \cos(n\theta) C_n(\cosh\eta_0)P_{n-\frac{1}{2}}(\cosh\eta) \, , </math> |
where,
|
<math>~D_0 </math> |
<math>~\equiv</math> |
<math>~ \frac{2^{3/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] = \frac{2^{3/2} }{3\pi^2} \biggl[\frac{(R^2 - d^2)^{3 / 2}}{d^2 R} \biggr] \, ,</math> |
|
<math>~C_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~(n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh \eta_0) Q_{n - \frac{1}{2}}^2(\cosh \eta_0) - (n - \tfrac{3}{2}) Q_{n - \frac{1}{2}}(\cosh \eta_0)~Q^2_{n + \frac{1}{2}}(\cosh \eta_0) \, </math> |
and where, in terms of the major ( R ) and minor ( d ) radii of the torus — or their ratio, ε ≡ d/R,
|
<math>~\cosh\eta_0</math> |
<math>~=</math> |
<math>~\frac{R}{d} = \frac{1}{\epsilon} \, ,</math> |
|
<math>~\sinh\eta_0</math> |
<math>~=</math> |
<math>~\frac{a}{d} = \frac{1}{d}\biggl[ R^2 - d^2 \biggr]^{1 / 2} = \frac{1}{\epsilon} \biggl[1 - \epsilon^2 \biggr]^{1 / 2} \, .</math> |
These expressions incorporate a number of basic elements of a toroidal coordinate system. In what follows, we will also make use of the following relations:
|
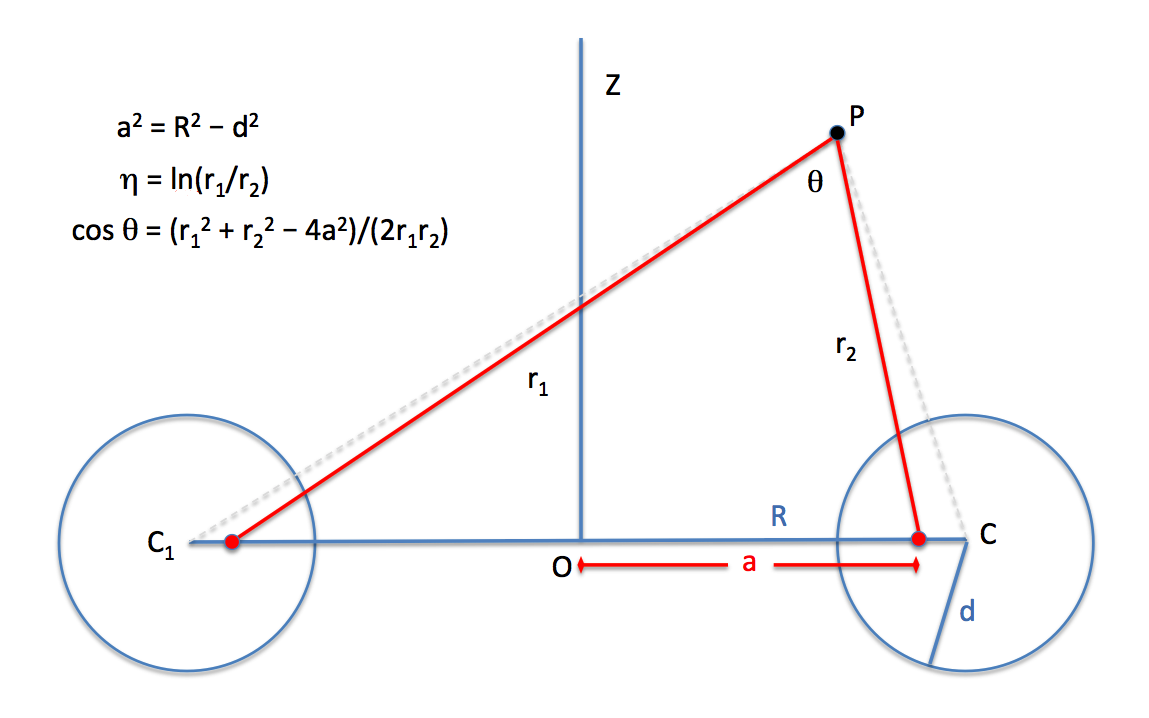
Once the primary scale factor, <math>~a</math>, has been specified, the illustration shown at the bottom of this inset box — see also our accompanying set of similar figures used by other researchers — helps in explaining how transformations can be made between any two of the referenced coordinate pairs: <math>~(\varpi, z)</math>, <math>~(\eta, \theta)</math>, <math>~(r_1, r_2)</math>.
Given that (sin2θ + cos2θ) = 1, we have,
We deduce as well that,
Given the definitions,
we can use the transformations,
Or we can use the transformations,
Additional potentially useful relations can be found in an accompanying chapter wherein we present a variety of basic elements of a toroidal coordinate system. |
Leading (n = 0) Term
Wong's Expression
Now, from our separate derivation we have,
|
<math>~P_{-1 / 2}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} Q_{-1 / 2}(\coth\eta) \, . </math> |
And if we make the function-argument substitution, <math>~z \rightarrow \coth\eta</math>, in the "Key Equation,"
|
<math>~Q_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3) |
|||
we can write,
|
<math>~P_{-1 / 2}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) \, , </math> |
where, from above, we recognize that,
<math>~ k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} \, . </math>
So, the leading (n = 0) term gives,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~C_0(\cosh\eta_0)P_{-\frac{1}{2}}(\cosh\eta) </math> |
|
|
<math>~=</math> |
<math>~ -D_0~C_0(\cosh\eta_0) \biggl[ \frac{a \sinh\eta}{\varpi} \biggr]^{1 / 2} ~\frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{D_0~C_0(\cosh\eta_0)}{\pi} \biggl[ \frac{2a }{\varpi} \biggr]^{1 / 2} ~ k \boldsymbol{K}(k) </math> |
|
|
<math>~=</math> |
<math>~ - C_0(\cosh\eta_0) \cdot \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . </math> |
Thin-Ring Evaluation of C0
In an accompanying discussion of the thin-ring approximation, we showed that as <math>~\cosh\eta_0 \rightarrow \infty</math>
|
<math>~C_0(x)\biggr|_{x\rightarrow \infty}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3 \pi^2}{2^2} \biggr) \frac{1}{\cosh^2\eta_0} \, . </math> |
Hence, in this limit we can write,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{thin-ring}</math> |
<math>~=</math> |
<math>~ - \frac{2 }{\pi} \cancelto{1}{\biggl[\frac{\sinh\eta_0}{\cosh\eta_0}\biggr]^3 } \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, . </math> |
More General Evaluation of C0
|
NOTE of CAUTION: In our above evaluation of the toroidal function, <math>~Q_{-\frac{1}{2}}(z)</math>, we appropriately associated the function argument, <math>~z</math>, with the hyperbolic-cotangent of <math>~\eta</math>; that is, we made the substitution, <math>~z \rightarrow \coth\eta</math>. Here, as we assess the behavior of, and evaluate, the leading coefficient, <math>~C_0</math>, an alternate substitution is appropriate, namely, <math>~z_0 \rightarrow \cosh\eta_0</math>; we affix the subscript zero to this function argument in an effort to minimize possible confusion with the argument, <math>~z</math>. |
Drawing from our accompanying tabulation of Toroidal Function Evaluations, we have more generally,
|
<math>~2C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl[ Q_{+\frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q_{ - \frac{1}{2}}^2(\cosh \eta_0) \biggr] + 3 \biggl[ Q_{ - \frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q^2_{ + \frac{1}{2}}(\cosh \eta_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \cosh\eta_0 ~k_0~K(k_0) ~-~ [2(\cosh\eta_0+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{3} (\cosh\eta_0+1) (\cosh\eta_0-1)^{2} ]^{1 / 2}} \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{2}{(\cosh\eta_0 - 1)(\cosh^2\eta_0 -1)} \biggr]^{1 / 2} E(k_0) \biggr\} \, , </math> |
where,
|
<math>~k_0</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{2}{\cosh\eta_0+1}\biggr]^{1 / 2} ~~~\Rightarrow ~~~ (\cosh\eta_0 + 1) = \frac{2}{k_0^2} \, .</math> |
|
Looking back at our previous numerical evaluation of <math>~C_0(\cosh\eta_0)</math> when <math>~z_0 = \cosh\eta_0 = 3 ~~\Rightarrow ~~~ k_0 = 2^{-1 / 2}</math>, we see that,
|
Attempting to simplify this expression, we have,
|
<math>~2C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl\{ \cosh\eta_0 ~k_0~K(k_0) ~-~ \biggl(\frac{2}{k_0}\biggr) E(k_0) \biggr\} \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{2} k_0^{-1} (\cosh\eta_0-1) ]} \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{k_0^2}{(\cosh\eta_0 - 1)^2} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
<math>~\Rightarrow ~~~ 2^3(\cosh\eta_0 - 1)C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ \biggl\{ \cosh\eta_0 ~k_0^2~K(k_0) ~-~ 2 E(k_0) \biggr\} \times \biggl\{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) \biggr\} </math> |
|
|
|
<math>~ - 3 k_0 ~K ( k_0) \times \biggl\{ \cosh\eta_0(\cosh\eta_0 - 1)~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) k_0 E(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 ~k_0^2 + 3\cosh\eta_0~ (\cosh\eta_0~-1)k_0^2\biggr] </math> |
|
|
|
<math>~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 ~k_0^2 + 2(\cosh\eta_0 ~-1) + 3k_0^2 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[2^3\cosh\eta_0 \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{ 2^3(\cosh\eta_0 - 1)}{k_0^2} \biggr] C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 + 3\cosh\eta_0~ (\cosh\eta_0~-1) \biggr] </math> |
|
|
|
<math>~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 + \frac{2}{k_0^2}(\cosh\eta_0 ~-1) + 3 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[\frac{2^3\cosh\eta_0}{k_0^2} \biggr] </math> |
|
<math>~\Rightarrow ~~~ (\cosh^2\eta_0 - 1) C_0(\cosh\eta_0)</math> |
<math>~=</math> |
<math>~ K(k_0)\cdot K(k_0) \biggl[ \cosh\eta_0(1 - \cosh\eta_0) \biggr] + 2K(k_0)\cdot E(k_0) \biggl[ \cosh^2\eta_0 + 1\biggr] - E(k_0)\cdot E(k_0) \biggl[ \cosh\eta_0(1 + \cosh\eta_0) \biggr] </math> |
This last, simplifed expression gives, as above, <math>~C_0(3) = 0.945933523</math>. TERRIFIC!
Finally then, for any choice of <math>~\eta_0</math>,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{exterior}</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) </math> |
|
|
|
<math>~ \times \biggl\{ K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] - E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] \biggr\} \, . </math> |
Second (n = 1) Term
The second (n = 1) term in Wong's (1973) expression for the exterior potential is,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos\theta \cdot C_1(\cosh\eta_0)P_{+\frac{1}{2}}(\cosh\eta) \, , </math> |
where, <math>~D_0</math> is the same as above, and,
|
<math>~C_1(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~\tfrac{3}{2} Q_{+\frac{3}{2}}(\cosh \eta_0) Q_{+\frac{1}{2}}^2(\cosh \eta_0) + \tfrac{1}{2} Q_{+\frac{1}{2}}(\cosh \eta_0)~Q^2_{+ \frac{3}{2}}(\cosh \eta_0) \, . </math> |
Now, from our accompanying table of "Toroidal Function Evaluations", it appears as though,
|
<math>~P_{+\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~\frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} E(k) \, ,</math> |
where, as above,
|
<math>~k</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{2}{\coth\eta+1} \biggr]^{1 / 2} \, .</math> |
Hence, we have,
|
<math>~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \cos\theta \cdot (\cosh\eta - \cos\theta)^{1 / 2} (\sinh\eta)^{+1 / 2} \biggr] k^{-1} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \frac{a\sinh^2\eta}{\varpi} \cdot \frac{\coth\eta + 1}{2} \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2\varpi} \biggr) \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2} \biggr)\biggl[ \frac{4a}{r_1^2 - r_2^2} \biggr] \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{r_2} \biggr] E(k) = - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{\sqrt{ (\varpi - a)^2 + (z-Z_0)^2 }} \biggr] E(k) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] \boldsymbol{E}(k) \, . </math> |
|
From the above function tabulations & evaluations — for example, <math>~ K(k_0) = 1.854074677</math> and <math>~ E(k_0) = 1.350643881</math> — and a separate listing of Example Recurrence Relations, we have,
Then, letting <math>~\mu \rightarrow 2</math> and, for all m ≥ 2, letting <math>~\nu \rightarrow (m - \tfrac{1}{2})</math> in the "Key Equation,"
we have,
Therefore, specifically for m = 1, we obtain the recurrence relation,
| |||||||||||||||||||||||||||||||||||||||||||||
While keeping in mind that,
|
<math>~z_0</math> |
<math>~=</math> |
<math>~\cosh\eta_0 \, ,</math> |
and, |
<math>~k_0^2</math> |
<math>~=</math> |
<math>~\frac{2}{\coth\eta_0 + 1} = \frac{2(z_0^2-1)^{1 / 2}}{z_0 + (z_0^2 - 1)^{1 / 2}} \, ,</math> |
let's attempt to express this leading coefficient, <math>~C_1(\cosh\eta_0)</math>, entirely in terms of the pair of complete elliptic integral functions.
|
<math>~2C_1(z_0)</math> |
<math>~=</math> |
<math>~3 \biggl[ Q_{+\frac{3}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl[3 Q_{+\frac{3}{2}}(z_0) -4z Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ 5Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q^{2}_{- \tfrac{1}{2}}(z_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~-~\frac{1}{2^2}\biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) -4z \biggl[ z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \biggr\} \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
|
|
<math>~ + 5\biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ [2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{2^2} \cdot k_0 K(k_0) \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\} </math> |
|
|
|
<math>~ + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ 4zE(k_0) - (z-1)K(k_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ K(k_0)\cdot K(k_0) \biggl\{ \frac{z k_0^2}{2^2} - 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot zk_0(z-1)\biggr\} + E(k_0)\cdot E(k_0) \biggl\{ -5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot 4z \biggr\} </math> |
|
|
|
<math>~ +~K(k_0)\cdot E(k_0) \biggl\{ -~\frac{1}{2^2} \cdot k_0(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 + 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) \biggr\} \, . </math> |
Hence,
|
<math>~2[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> |
<math>~=</math> |
<math>~ z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} -~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0) </math> |
|
|
|
<math>~ +~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + 5(z-1) [2(z+1)]^{1 / 2} \biggr\} </math> |
|
<math>~\Rightarrow ~~~ 2^{5 / 2}[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math> |
<math>~=</math> |
<math>~ zk_0(z-1) \cdot K(k_0)\cdot K(k_0) \biggl\{ k_0 [2(z+1) ]^{1 / 2} - 5 \biggr\} -~20 z[2(z+1)]^{1 / 2} \cdot E(k_0)\cdot E(k_0) </math> |
|
|
|
<math>~ +~K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + 5(z-1) [2(z+1)]^{1 / 2} \biggr\} \, . </math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |