From VisTrailsWiki

(Difference between revisions)

Revision as of 21:52, 26 June 2020

Université de Bordeaux

Spheroid-Ring Systems

Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.

Exterior Gravitational Potential of Toroids

J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.

Their Presentation

On an initial reading, it appears as though the most relevant section of the Huré, et al. (2020) paper is §8 titled, The Solid Torus. They write the gravitational potential in terms of the series expansion,

$~\Psi_\mathrm{grav}(\vec{r})$

$~\approx$

$~ \Psi_0 + \sum\limits_{n=1}^N \Psi_n \, ,$

Huré, et al. (2020), §7, p. 5831, Eq. (42)

where, after setting $~M_\mathrm{tot} = 2\pi^2\rho_0 b^2 R_c$ and acknowledging that $~V_{0,0} = 1 \, ,$ we can write,

$~\Psi_0$

$~=$

$~ - \frac{GM_\mathrm{tot}}{r} \biggl[ \frac{r}{\Delta_0} \cdot \frac{2}{\pi} \boldsymbol{K}(k_0) \biggr]$

Huré, et al. (2020), §8, p. 5832, Eqs. (52) & (53)

and,

$~\frac{1}{e^2} \biggl[ \Psi_1 + \Psi_2 \biggr]$

$~=$

$~ - \frac{G\pi \rho_0 R_c b^2}{4 (k')^2 \Delta_0^3} \biggl\{ [\Delta_0^2 - 2R_c(R_c + R)]\boldsymbol{E}(k) - (k')^2 \Delta_0^2 \boldsymbol{K}(k) \biggr\} \, .$

Huré, et al. (2020), §8, p. 5832, Eq. (54)

Note that the argument of the elliptic integral functions is,

$~k$

$~\equiv$

$~ \frac{2\sqrt{\varpi R}}{\Delta}$

where,

$~\Delta$

$~\equiv$

$~ \biggl[ (R + \varpi)^2 + (Z-z)^2 \biggr]^{1 / 2} \, .$

Huré, et al. (2020), §2, p. 5826, Eqs. (4) & (5)

Our Presentation of Wong's (1973) Result

Setup

From our accompanying discussion of Wong's (1973) derivation, the exterior potential is given by the expression,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W}(\eta,\theta)$

$~=$

$~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~\sum_{n=0}^{\mathrm{nmax}} \epsilon_n \cos(n\theta) C_n(\cosh\eta_0)P_{n-\frac{1}{2}}(\cosh\eta) \, ,$

where,

$~D_0$	$~\equiv$	$~ \frac{2^{3/2} }{3\pi^2} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] = \frac{2^{3/2} }{3\pi^2} \biggl[\frac{(R^2 - d^2)^{3 / 2}}{d^2 R} \biggr] \, ,$
$~C_n(\cosh\eta_0)$	$~\equiv$	$~(n+\tfrac{1}{2})Q_{n+\frac{1}{2}}(\cosh \eta_0) Q_{n - \frac{1}{2}}^2(\cosh \eta_0) - (n - \tfrac{3}{2}) Q_{n - \frac{1}{2}}(\cosh \eta_0)~Q^2_{n + \frac{1}{2}}(\cosh \eta_0) \,$

and where, in terms of the major ( R ) and minor ( d ) radii of the torus — or their ratio, ε ≡ d/R,

$~\cosh\eta_0$	$~=$	$~\frac{R}{d} = \frac{1}{\epsilon} \, ,$
$~\sinh\eta_0$	$~=$	$~\frac{a}{d} = \frac{1}{d}\biggl[ R^2 - d^2 \biggr]^{1 / 2} = \frac{1}{\epsilon} \biggl[1 - \epsilon^2 \biggr]^{1 / 2} \, .$

These expressions incorporate a number of basic elements of a toroidal coordinate system. In what follows, we will also make use of the following relations:

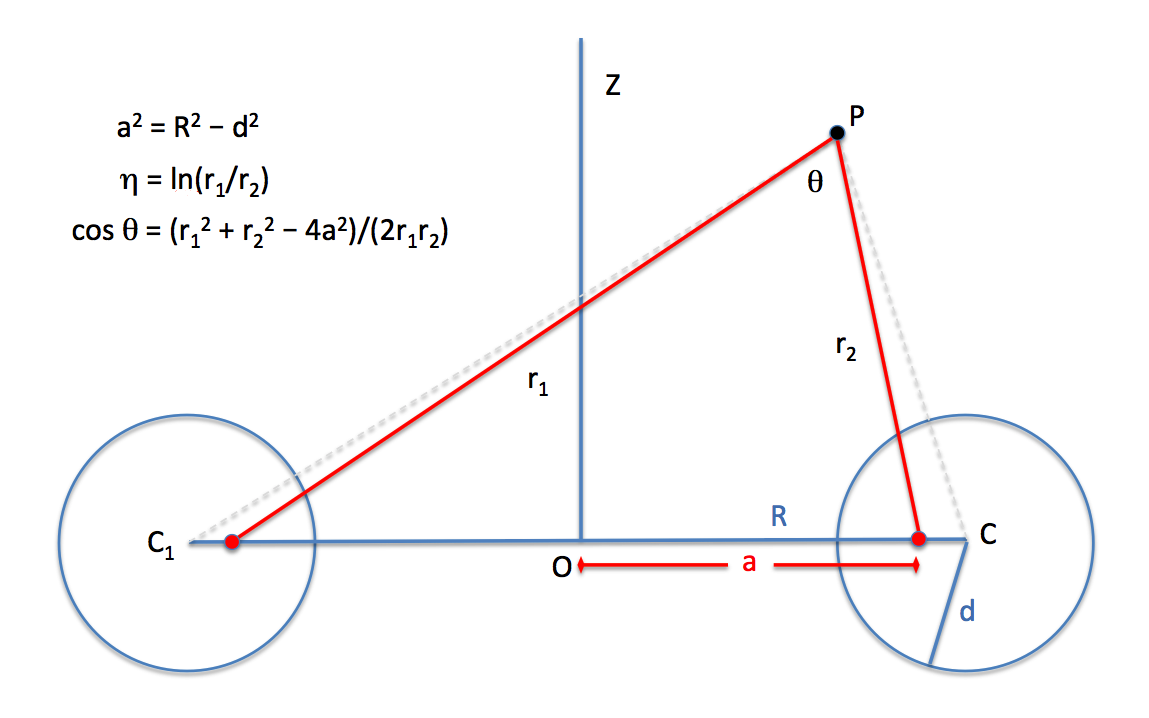
Once the primary scale factor, $~a$ , has been specified, the illustration shown at the bottom of this inset box — see also our accompanying set of similar figures used by other researchers — helps in explaining how transformations can be made between any two of the referenced coordinate pairs: $~(\varpi, z)$ , $~(\eta, \theta)$ , $~(r_1, r_2)$ .

$~\varpi$	$~=$	$~\frac{a\sinh\eta}{(\cosh\eta - \cos\theta)}$	$~\Rightarrow ~$	$~\cos\theta$	$~=$	$~\cosh\eta - \frac{a\sinh\eta}{\varpi}$
$~z - Z_0$	$~=$	$~\frac{a\sin\theta}{(\cosh\eta - \cos\theta)}$	$~\Rightarrow ~$	$~\sin\theta$	$~=$	$~\frac{(z - Z_0)}{\varpi} \cdot \sinh\eta$

Given that (sin²θ + cos²θ) = 1, we have,

$~1$	$~=$	$~ \biggl[ \frac{(z - Z_0)}{\varpi} \cdot \sinh\eta \biggr]^2 + \biggl[\cosh\eta - \frac{a\sinh\eta}{\varpi}\biggr]^2$
$~\Rightarrow ~~~ \coth\eta$	$~=$	$~ \frac{1}{2a\varpi}\biggl[\varpi^2 + a^2 + (z - Z_0)^2 \biggr] \, .$

We deduce as well that,

$~\frac{2}{\coth\eta + 1}$	$~=$	$~ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \, ,$ and,
$~\sinh\eta + \cosh\eta$	$~=$	$~ \frac{\varpi^2 + a^2 + (z - Z_0)^2}{(\varpi + a)^2 + (z - Z_0)^2} \, .$

Given the definitions,

$~r_1^2$	$~=$	$~(\varpi + a)^2 + (z - Z_0)^2 \, ,$
$~r_2^2$	$~=$	$~(\varpi - a)^2 + (z - Z_0)^2 \, ,$

we can use the transformations,

$~\varpi$	$~=$	$~\frac{(r_1^2 - r_2^2)}{4a}$ and,
$~(z - Z_0)^2$	$~=$	$~r_2^2 - \frac{1}{16a^2}\biggl[ r_1^2 - r_2^2 - 4a^2 \biggr]^2 \, ,$ or,
$~(z - Z_0)^2$	$~=$	$~r_1^2 - \frac{1}{16a^2}\biggl[ r_1^2 - r_2^2 + 4a^2 \biggr]^2 \, .$

Or we can use the transformations,

$~\eta$	$~=$	$~\ln \biggl(\frac{r_1}{r_2}\biggr) \, ,$
$~\cos\theta$	$~=$	$~\frac{r_1^2 + r_2^2 - 4a^2}{2r_1 r_2} \, .$

Additional potentially useful relations can be found in an accompanying chapter wherein we present a variety of basic elements of a toroidal coordinate system.

Leading (n = 0) Term

Wong's Expression

Now, from our separate derivation we have,

$~P_{-1 / 2}(\cosh\eta)$

$~=$

$~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} Q_{-1 / 2}(\coth\eta) \, .$

And if we make the function-argument substitution, $~z \rightarrow \coth\eta$ , in the "Key Equation,"

	$~Q_{-\frac{1}{2}}(z)$	$~=$	$~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr)$
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3)

we can write,

$~P_{-1 / 2}(\cosh\eta)$

$~=$

$~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k) \, ,$

where, from above, we recognize that,

$~ k \equiv \biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{4a\varpi}{(\varpi + a)^2 + (z - Z_0)^2} \biggr]^{1 / 2} \, .$

So, the leading (n = 0) term gives,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)$	$~=$	$~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} ~C_0(\cosh\eta_0)P_{-\frac{1}{2}}(\cosh\eta)$
	$~=$	$~ -D_0~C_0(\cosh\eta_0) \biggl[ \frac{a \sinh\eta}{\varpi} \biggr]^{1 / 2} ~\frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} ~k \boldsymbol{K}(k)$
	$~=$	$~ -\frac{D_0~C_0(\cosh\eta_0)}{\pi} \biggl[ \frac{2a }{\varpi} \biggr]^{1 / 2} ~ k \boldsymbol{K}(k)$
	$~=$	$~ - C_0(\cosh\eta_0) \cdot \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, .$

Thin-Ring Evaluation of C₀

In an accompanying discussion of the thin-ring approximation, we showed that as $~\cosh\eta_0 \rightarrow \infty$

$~C_0(x)\biggr|_{x\rightarrow \infty}$

$~=$

$~\biggl( \frac{3 \pi^2}{2^2} \biggr) \frac{1}{\cosh^2\eta_0} \, .$

Hence, in this limit we can write,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr|_\mathrm{thin-ring}$

$~=$

$~ - \frac{2 }{\pi} \cancelto{1}{\biggl[\frac{\sinh\eta_0}{\cosh\eta_0}\biggr]^3 } \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k) \, .$

More General Evaluation of C₀

NOTE of CAUTION: In our above evaluation of the toroidal function, $~Q_{-\frac{1}{2}}(z)$ , we appropriately associated the function argument, $~z$ , with the hyperbolic-cotangent of $~\eta$ ; that is, we made the substitution, $~z \rightarrow \coth\eta$ . Here, as we assess the behavior of, and evaluate, the leading coefficient, $~C_0$ , an alternate substitution is appropriate, namely, $~z_0 \rightarrow \cosh\eta_0$ ; we affix the subscript zero to this function argument in an effort to minimize possible confusion with the argument, $~z$ .

Drawing from our accompanying tabulation of Toroidal Function Evaluations, we have more generally,

$~2C_0(\cosh\eta_0)$	$~=$	$~ \biggl[ Q_{+\frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q_{ - \frac{1}{2}}^2(\cosh \eta_0) \biggr] + 3 \biggl[ Q_{ - \frac{1}{2}}(\cosh \eta_0) \biggr] \biggl[ Q^2_{ + \frac{1}{2}}(\cosh \eta_0) \biggr]$
	$~=$	$~ \biggl[ \cosh\eta_0 ~k_0~K(k_0) ~-~ [2(\cosh\eta_0+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{3} (\cosh\eta_0+1) (\cosh\eta_0-1)^{2} ]^{1 / 2}} \biggr\}$
		$~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{2}{(\cosh\eta_0 - 1)(\cosh^2\eta_0 -1)} \biggr]^{1 / 2} E(k_0) \biggr\} \, ,$

where,

$~k_0$

$~\equiv$

$~\biggl[ \frac{2}{\cosh\eta_0+1}\biggr]^{1 / 2} ~~~\Rightarrow ~~~ (\cosh\eta_0 + 1) = \frac{2}{k_0^2} \, .$

Looking back at our previous numerical evaluation of $~C_0(\cosh\eta_0)$ when $~z_0 = \cosh\eta_0 = 3 ~~\Rightarrow ~~~ k_0 = 2^{-1 / 2}$ , we see that,

Appendix Expression: $~Q_{-\tfrac{1}{2}}(z_0)$	$~=$	$~k_0 K(k_0)$
Hence MF53 value, $~Q_{-\tfrac{1}{2}}(3)$	$~=$	$~1.311028777 ~~~\Rightarrow ~~~ K(k_0) = 1.854074677$
Appendix Expression: $~Q_{+\tfrac{1}{2}}(z_0)$	$~=$	$~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)$
Hence MF53 value, $~Q_{+\tfrac{1}{2}}(3)$	$~=$	$~0.1128885424 ~~~\Rightarrow~~~ E(k_0) = 1.350643881$
Appendix Expression: $~Q^2_{-\tfrac{1}{2}}(z_0)$	$~=$	$~[2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)]$
Hence, $~Q^2_{-\tfrac{1}{2}}(3)$	$~=$	$~1.104816977$ , which matches MF53 value
Additional derivation: $~Q^2_{+\tfrac{1}{2}}(z_0)$	$~=$	$~ -~\frac{1}{2^2}\biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0)\biggr\}$
Hence, $~Q^2_{+\tfrac{1}{2}}(3)$	$~=$	$~0.449302588$

$~\Rightarrow ~~~ C_0(3)$

$~=$

$~ \frac{1}{2}~Q_{+\frac{1}{2}}(3) \cdot Q_{- \frac{1}{2}}^2(3) + \frac{3}{2}~ Q_{- \frac{1}{2}}(3)\cdot Q^2_{+ \frac{1}{2}}(3) = 0.945933522 \, .$

Attempting to simplify this expression, we have,

$~2C_0(\cosh\eta_0)$	$~=$	$~ \biggl\{ \cosh\eta_0 ~k_0~K(k_0) ~-~ \biggl(\frac{2}{k_0}\biggr) E(k_0) \biggr\} \times \biggl\{ \frac{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) }{ [2^{2} k_0^{-1} (\cosh\eta_0-1) ]} \biggr\}$
		$~ - \frac{3}{2^2} \biggl[ k_0 ~K ( k_0) \biggr] \times \biggl\{ \cosh\eta_0~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) \biggl[ \frac{k_0^2}{(\cosh\eta_0 - 1)^2} \biggr]^{1 / 2} E(k_0) \biggr\}$
$~\Rightarrow ~~~ 2^3(\cosh\eta_0 - 1)C_0(\cosh\eta_0)$	$~=$	$~ \biggl\{ \cosh\eta_0 ~k_0^2~K(k_0) ~-~ 2 E(k_0) \biggr\} \times \biggl\{ 4 \cosh\eta_0 ~E(k_0) - (\cosh\eta_0-1) K(k_0) \biggr\}$
		$~ - 3 k_0 ~K ( k_0) \times \biggl\{ \cosh\eta_0(\cosh\eta_0 - 1)~ k_0~K ( k_0 ) ~-~(\cosh^2\eta_0+3) k_0 E(k_0) \biggr\}$
	$~=$	$~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 ~k_0^2 + 3\cosh\eta_0~ (\cosh\eta_0~-1)k_0^2\biggr]$
		$~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 ~k_0^2 + 2(\cosh\eta_0 ~-1) + 3k_0^2 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[2^3\cosh\eta_0 \biggr]$
$~\Rightarrow ~~~ \biggl[ \frac{ 2^3(\cosh\eta_0 - 1)}{k_0^2} \biggr] C_0(\cosh\eta_0)$	$~=$	$~ -~K(k_0)\cdot K(k_0) \biggl[ (\cosh\eta_0-1) \cdot \cosh\eta_0 + 3\cosh\eta_0~ (\cosh\eta_0~-1) \biggr]$
		$~ + K(k_0)\cdot E(k_0) \biggl[ 2^2 \cosh^2\eta_0 + \frac{2}{k_0^2}(\cosh\eta_0 ~-1) + 3 (\cosh^2\eta_0 ~ + 3)\biggr] - E(k_0)\cdot E(k_0) \biggl[\frac{2^3\cosh\eta_0}{k_0^2} \biggr]$
$~\Rightarrow ~~~ (\cosh^2\eta_0 - 1) C_0(\cosh\eta_0)$	$~=$	$~ K(k_0)\cdot K(k_0) \biggl[ \cosh\eta_0(1 - \cosh\eta_0) \biggr] + 2K(k_0)\cdot E(k_0) \biggl[ \cosh^2\eta_0 + 1\biggr] - E(k_0)\cdot E(k_0) \biggl[ \cosh\eta_0(1 + \cosh\eta_0) \biggr]$

This last, simplifed expression gives, as above, $~C_0(3) = 0.945933523$ . TERRIFIC!

Finally then, for any choice of $~\eta_0$ ,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W0}(\eta,\theta)\biggr\|_\mathrm{exterior}$	$~=$	$~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh\eta_0}{\cosh\eta_0}\biggr] \frac{a}{ [ (\varpi + a)^2 + (z - Z_0)^2 ]^{1 / 2} } \cdot \boldsymbol{K}(k)$
		$~ \times \biggl\{ K(k_0)\cdot K(k_0) [ \cosh\eta_0(1 - \cosh\eta_0) ] + 2K(k_0)\cdot E(k_0) [ \cosh^2\eta_0 + 1 ] - E(k_0)\cdot E(k_0) [ \cosh\eta_0(1 + \cosh\eta_0) ] \biggr\} \, .$

Second (n = 1) Term

The second (n = 1) term in Wong's (1973) expression for the exterior potential is,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)$

$~=$

$~ -D_0 (\cosh\eta - \cos\theta)^{1 / 2} \cdot 2 \cos\theta \cdot C_1(\cosh\eta_0)P_{+\frac{1}{2}}(\cosh\eta) \, ,$

where, $~D_0$ is the same as above, and,

$~C_1(\cosh\eta_0)$

$~\equiv$

$~\tfrac{3}{2} Q_{+\frac{3}{2}}(\cosh \eta_0) Q_{+\frac{1}{2}}^2(\cosh \eta_0) + \tfrac{1}{2} Q_{+\frac{1}{2}}(\cosh \eta_0)~Q^2_{+ \frac{3}{2}}(\cosh \eta_0) \, .$

Now, from our accompanying table of "Toroidal Function Evaluations", it appears as though,

$~P_{+\frac{1}{2}}(\cosh\eta)$

$~=$

$~\frac{\sqrt{2}}{\pi} (\sinh\eta)^{+1 / 2} k^{-1} E(k) \, ,$

where, as above,

$~k$

$~\equiv$

$~\biggl[ \frac{2}{\coth\eta+1} \biggr]^{1 / 2} \, .$

Hence, we have,

$~\biggl( \frac{a}{GM} \biggr) \Phi_\mathrm{W1}(\eta,\theta)$	$~=$	$~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \cos\theta \cdot (\cosh\eta - \cos\theta)^{1 / 2} (\sinh\eta)^{+1 / 2} \biggr] k^{-1} E(k)$
	$~=$	$~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \frac{a\sinh^2\eta}{\varpi} \cdot \frac{\coth\eta + 1}{2} \biggr\}^{1 / 2} E(k)$
	$~=$	$~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2\varpi} \biggr) \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k)$
	$~=$	$~ - \frac{2^{3} }{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \cdot \cos\theta \biggl\{ \biggl( \frac{a}{2} \biggr)\biggl[ \frac{4a}{r_1^2 - r_2^2} \biggr] \biggl[ \frac{r_1^2 - r_2^2}{2r_1 r_2} \biggr]^2 \cdot \biggl[ \frac{2r_1^2}{r_1^2 - r_2^2} \biggr] \biggr\}^{1 / 2} E(k)$
	$~=$	$~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{r_2} \biggr] E(k) = - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[ \frac{\cos\theta}{\sqrt{ (\varpi - a)^2 + (z-Z_0)^2 }} \biggr] E(k)$
	$~=$	$~ - \frac{2^{3} a}{3\pi^3} \biggl[ \frac{\sinh^3\eta_0}{\cosh\eta_0}\biggr] C_1(\cosh\eta_0) \biggl[\frac{ r_1^2 + r_2^2 - 4a^2}{2r_1 r_2^2} \biggr] \boldsymbol{E}(k) \, .$

From the above function tabulations & evaluations — for example, $~ K(k_0) = 1.854074677$ and $~ E(k_0) = 1.350643881$ — and a separate listing of Example Recurrence Relations, we have,

Appendix Expression: $~Q_{-\tfrac{1}{2}}(z_0)$	$~=$	$~k_0 K(k_0)$
Appendix Expression: $~Q_{+\tfrac{1}{2}}(z_0)$	$~=$	$~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)$
$~Q^0_{m-\tfrac{1}{2}}$ recurrence with m = 2: $~Q_{+\tfrac{3}{2}}(z_0)$	$~=$	$~\frac{4}{3} z~Q_{+\tfrac{1}{2}}(z_0) - \frac{1}{3} Q_{-\tfrac{1}{2}}(z_0)$
	$~=$	$~\frac{4}{3} z \{z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0)\} - \frac{1}{3}k_0 K(k_0)$
	$~=$	$~\frac{1}{3} \biggl[ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) \biggr]$
Hence, $~Q_{+\tfrac{3}{2}}(3)$	$~=$	$~0.014544576 \, .$

Appendix Expression: $~Q^2_{-\tfrac{1}{2}}(z_0)$	$~=$	$~[2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)]$
Additional derivation: $~Q^2_{+\tfrac{1}{2}}(z_0)$	$~=$	$~ -~\frac{1}{2^2}\biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0)\biggr\}$

Then, letting $~\mu \rightarrow 2$ and, for all m ≥ 2, letting $~\nu \rightarrow (m - \tfrac{1}{2})$ in the "Key Equation,"

	$~(\nu - \mu + 1)P^\mu_{\nu + 1} (z)$	$~=$	$~ (2\nu + 1)z P_\nu^\mu(z) - (\nu + \mu)P^\mu_{\nu-1}(z)$
Abramowitz & Stegun (1995), p. 334, eq. (8.5.3)

NOTE: $~Q_\nu^\mu$ , as well as $~P_\nu^\mu$ , satisfies this same recurrence relation.

we have,

$~(m - \tfrac{3}{2})Q^{2}_{m+\tfrac{1}{2}} (z)$

$~=$

$~ (2m)z Q_{m-\tfrac{1}{2}}^{2}(z) - (m + \tfrac{3}{2})Q^{2}_{m - \tfrac{3}{2}}(z) \, .$

Therefore, specifically for m = 1, we obtain the recurrence relation,

$~Q^{2}_{+\tfrac{3}{2}} (z_0)$	$~=$	$~ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \, ,$
Hence, $~Q^{2}_{+\tfrac{3}{2}} (3)$	$~=$	$~ 0.132453829 \, .$

$~\Rightarrow ~~~ C_1(3)$

$~=$

$~ \frac{3}{2}~Q_{+\frac{3}{2}}(3) \cdot Q_{+ \frac{1}{2}}^2(3) + \frac{1}{2}~ Q_{+ \frac{1}{2}}(3)\cdot Q^2_{+ \frac{3}{2}}(3) = 0.017278633 \, .$

While keeping in mind that,

$~z_0$

$~=$

$~\cosh\eta_0 \, ,$

and,

$~k_0^2$

$~=$

$~\frac{2}{\cosh\eta_0 + 1} = \frac{2}{z_0 + 1} \, ,$

let's attempt to express this leading coefficient, $~C_1(\cosh\eta_0)$ , entirely in terms of the pair of complete elliptic integral functions.

$~2C_1(z_0)$	$~=$	$~3 \biggl[ Q_{+\frac{3}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ 5 Q^{2}_{- \tfrac{1}{2}}(z_0)-4z Q_{+\tfrac{1}{2}}^{2}(z_0) \biggr]$
	$~=$	$~\biggl[3 Q_{+\frac{3}{2}}(z_0) -4z Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q_{+\frac{1}{2}}^2(z_0) \biggr] + \biggl[ 5Q_{+\frac{1}{2}}(z_0) \biggr]\times \biggl[ Q^{2}_{- \tfrac{1}{2}}(z_0) \biggr]$
	$~=$	$~-~\frac{1}{2^2}\biggl\{ (4z^2 - 1 )k_0 K(k_0) - 4 z[2(z+1)]^{1 / 2} E(k_0) -4z \biggl[ z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \biggr\} \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\}$
		$~ + 5\biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ [2^3(z-1)(z^2-1)]^{-1 / 2} [4zE(k_0) - (z-1)K(k_0)] \biggr\}$
	$~=$	$~\frac{1}{2^2} \cdot k_0 K(k_0) \times \biggl\{ z k_0~K ( k_0 ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k_0) \biggr\}$
		$~ + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \biggl[ ~z~k_0 K(k_0) - [2(z+1)]^{1 / 2} E(k_0) \biggr] \times \biggl\{ 4zE(k_0) - (z-1)K(k_0) \biggr\}$
	$~=$	$~ K(k_0)\cdot K(k_0) \biggl\{ \frac{z k_0^2}{2^2} - 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot zk_0(z-1)\biggr\} + E(k_0)\cdot E(k_0) \biggl\{ -5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot 4z \biggr\}$
		$~ +~K(k_0)\cdot E(k_0) \biggl\{ -~\frac{1}{2^2} \cdot k_0(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} + 5[2^3(z-1)(z^2-1)]^{-1 / 2} \cdot 4z^2k_0 + 5[2^3(z-1)(z^2-1)]^{-1 / 2}\cdot [2(z+1)]^{1 / 2} \cdot (z-1) \biggr\} \, .$

Hence,

$~2[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)$	$~=$	$~ z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[(z-1)(z^2-1) \biggr]^{1 / 2} - \frac{5(z-1)}{2^{3/2}} \biggr\} -~10 z(z+1)^{1 / 2} \cdot E(k_0)\cdot E(k_0)$
		$~ +~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + 5(z-1) [2(z+1)]^{1 / 2} \biggr\}$
$~\Rightarrow ~~~2^{3/2}\biggl[ \frac{(z-1)}{k_0} \biggr] C_1(z_0)$	$~=$	$~ z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[\frac{2^{1 / 2}(z-1)}{k_0} \biggr] - \frac{5(z-1)}{2^{3/2}} \biggr\} -~\biggl[ \frac{2^{3 / 2} \cdot 5z}{k_0} \biggr] E(k_0)\cdot E(k_0)$
		$~ +~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{ k_0[19z^2 - 3 ] + \frac{10 (z-1)}{k_0} \biggr\}$
$~\Rightarrow ~~~C_1(z_0)$	$~=$	$~ -~\biggl[ \frac{z}{(z+1)} \biggr] K(k_0)\cdot K(k_0) -~\biggl[ \frac{ 5z}{(z-1)} \biggr] E(k_0)\cdot E(k_0) +~\biggl[ \frac{2(3z^2 - 1)}{(z^2-1)} \biggr]K(k_0)\cdot E(k_0)$

@@ Line 1,359: / Line 1,359: @@
    </td>
    <td align="left">
-<math>~\frac{2}{\coth\eta_0 + 1}
+<math>~\frac{2}{\cosh\eta_0 + 1}
 =
-\frac{2(z_0^2-1)^{1 / 2}}{z_0 + (z_0^2 - 1)^{1 / 2}}
+\frac{2}{z_0 + 1}
 \, ,</math>
    </td>
@@ Line 1,537: / Line 1,537: @@
 <tr>
    <td align="right">
-<math>~\Rightarrow ~~~ 2^{5 / 2}[(z-1)(z^2-1)]^{1 / 2} C_1(z_0)</math>
+<math>~\Rightarrow ~~~2^{3/2}\biggl[ \frac{(z-1)}{k_0} \biggr] C_1(z_0)</math>
    </td>
    <td align="center">
@@ Line 1,544: / Line 1,544: @@
    <td align="left">
 <math>~
-zk_0(z-1) \cdot K(k_0)\cdot K(k_0) \biggl\{ k_0 [2(z+1) ]^{1 / 2}  - 5 \biggr\}
+z k_0 \cdot K(k_0)\cdot K(k_0) \biggl\{ \frac{k_0}{2^2} \biggl[\frac{2^{1 / 2}(z-1)}{k_0} \biggr]  - \frac{5(z-1)}{2^{3/2}} \biggr\}
--~20 z[2(z+1)]^{1 / 2}  \cdot E(k_0)\cdot E(k_0)
+-~\biggl[ \frac{2^{3 / 2} \cdot 5z}{k_0}  \biggr] E(k_0)\cdot E(k_0)
 </math>
    </td>
@@ Line 1,559: / Line 1,559: @@
    <td align="left">
 <math>~
-+~K(k_0)\cdot E(k_0) \biggl\{
++~2^{-3/2} K(k_0)\cdot E(k_0) \biggl\{
 k_0[19z^2 - 3 ]
-+ 5(z-1) [2(z+1)]^{1 / 2}
++ \frac{10 (z-1)}{k_0}
-\biggr\} \, .
+\biggr\}
+</math>
+  </td>
+</tr>
+<tr>
+  <td align="right">
+<math>~\Rightarrow ~~~C_1(z_0)</math>
+  </td>
+  <td align="center">
+<math>~=</math>
+  </td>
+  <td align="left">
+<math>~
+-~\biggl[ \frac{z}{(z+1)} \biggr] K(k_0)\cdot K(k_0)
+-~\biggl[ \frac{ 5z}{(z-1)}  \biggr] E(k_0)\cdot E(k_0)
++~\biggl[ \frac{2(3z^2 - 1)}{(z^2-1)}      \biggr]K(k_0)\cdot E(k_0)
 </math>
    </td>

User:Tohline/Appendix/Ramblings/Bordeaux

From VisTrailsWiki

Revision as of 21:52, 26 June 2020

Contents

Université de Bordeaux

Spheroid-Ring Systems

Exterior Gravitational Potential of Toroids

Their Presentation

Our Presentation of Wong's (1973) Result

Setup

Leading (n = 0) Term

Wong's Expression

Thin-Ring Evaluation of C₀

More General Evaluation of C₀

Second (n = 1) Term

Views

Personal tools

Navigation

Search

Toolbox

User:Tohline/Appendix/Ramblings/Bordeaux

From VisTrailsWiki

Revision as of 21:52, 26 June 2020

Contents

Université de Bordeaux

Spheroid-Ring Systems

Exterior Gravitational Potential of Toroids

Their Presentation

Our Presentation of Wong's (1973) Result

Setup

Leading (n = 0) Term

Wong's Expression

Thin-Ring Evaluation of C0

More General Evaluation of C0

Second (n = 1) Term

Views

Personal tools

Navigation

Search

Toolbox

Thin-Ring Evaluation of C₀

More General Evaluation of C₀