User:Tohline/Appendix/Ramblings/BiPolytrope51AnalyticStability
Marginally Unstable (nc,ne) = (5,1) Bipolytropes
This Ramblings Appendix chapter provides some detailed trial derivations — mostly blind alleyways — in support of the accompanying, thorough discussion of this topic.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Fundamental Modes
We decided to examine, first, whether any model along each sequence marks a transition from dynamically stable to dynamically unstable configurations. We accomplished this by setting <math>~\sigma_c^2</math> = 0, then integrating the relevant LAWE from the center toward the surface for many different guesses of the core-envelope interface radius until an eigenfunction with no radial nodes — i.e., an eigenfunction associated with the fundamental mode of radial oscillation — was found whose behavior at the surface matched with high precision the physically desired surface boundary condition. We were successful in this endeavor. A marginally unstable model was identified on each of the six separate equilibrium sequences.
Equilibrium Properties of Marginally Unstable Models
Table 2 summarizes some of the equilibrium properties of these six models. For example, the second column of the table gives the value of the core-envelope interface radius, <math>~\xi_i</math>, associated with each marginally unstable model. The table also lists: the value of the model's dimensionless radius, <math>~R^*_\mathrm{surf}</math>, the key structural parameters, <math>~q</math> & <math>~\nu</math>, and the central-to-mean density associated with each model; and in each case the dimensionless thermal energy <math>~(\mathfrak{s})</math> and dimensionless gravitational potential energy <math>~(\mathfrak{w})</math> associated, separately, with the core and the envelope. Note that, once the pair of parameters, <math>~(\mu_e/\mu_c, \xi_i)</math>, has been specified, we can legitimately assign high-precision values to all of the other model parameters because they are analytically prescribed.
|
Table 2: Properties of Marginally Unstable Bipolytropes Having |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| <math>~\frac{\mu_e}{\mu_c}</math> | <math>~\xi_i</math> | <math>~R^*_\mathrm{surf}</math> | <math>~q \equiv \frac{r_\mathrm{core}}{R_\mathrm{surf}}</math> | <math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}}</math> | <math>~\frac{\rho_c}{\bar\rho}</math> | <math>~\mathfrak{s}_\mathrm{core}</math> | <math>~\mathfrak{w}_\mathrm{core}</math> | <math>~\mathfrak{s}_\mathrm{env}</math> | <math>~\mathfrak{w}_\mathrm{env}</math> |
| 1 | 1.6686460157 | 2.139737 | 0.53885819 | 0.497747626 | 8.51704656 | 3.021916335 | -3.356583022 | 1.47780476 | -5.642859167 |
| <math>~\tfrac{1}{2}</math> | 2.27925811317 | 5.146499 | 0.306021732 | 0.401776274 | 63.29514949 | 4.241287117 | -6.074241035 | 4.284931508 | -10.97819621 |
| 0.345 | 2.560146865247 | 9.554041 | 0.185160563 | 0.234302525 | 209.7739052 | 4.639705843 | -7.125754184 | 11.72861751 | -25.61089252 |
| <math>~\tfrac{1}{3}</math> | 2.582007485476 | 10.120558 | 0.176288391 | 0.218241608 | 230.4125398 | 4.667042505 | -7.200966267 | 13.15887139 | -28.45086152 |
| 0.309 | 2.6274239687695 | 11.464303 | 0.158362807 | 0.184796947 | 279.0788798 | 4.722277318 | -7.354156963 | 17.1374434 | -36.36528446 |
| <math>~\tfrac{1}{4}</math> | 2.7357711469398 | 15.895632 | 0.118924863 | 0.11071211 | 430.0444648 | 4.84592201 | -7.70305421 | 37.84289623 | -77.67458196 |
As was expected from our above discussion of virial equilibrium conditions, we found that to high precision for each of these equilibrium models,
|
<math> (\mathfrak{w}_\mathrm{core} ~+~\mathfrak{w}_\mathrm{env}) ~+~2(\mathfrak{s}_\mathrm{core} ~+~\mathfrak{s}_\mathrm{env}) </math> |
<math>~=</math> |
<math>~0 \, .</math> |
However, contrary to expectations, in no case did we find that <math>~\mathfrak{s}_\mathrm{core}/\mathfrak{s}_\mathrm{env} = 5</math>. That is to say, we found that none of the models lies on the (red-dashed) curve in the <math>~q-\nu</math> parameter space that separates stable from unstable models as defined by our above free-energy-based stability analysis. The left-hand panel of Figure 4 shows this (red-dashed) demarcation curve; for all intents and purposes, it is a reproduction of the right-hand panel of Figure 3, above — turning-point markers have been removed to minimize clutter, the equilibrium sequences have been labeled, and the horizontal axis has been extended to unity in order to include a longer portion of the <math>~\mu_e/\mu_c = 1</math> sequence. The orange triangular markers that appear in the right-hand panel of Figure 4 pinpoint where each of the Table 2 "marginally unstable" models resides in this <math>~q-\nu</math> plane. Clearly, all six of the orange triangles lie well off of — and to the stable side of — the red-dashed demarcation curve. This discrepancy, which has resulted from our use of two separate approaches to stability analysis, will be discussed further and gratifyingly resolved, below.
| Figure 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
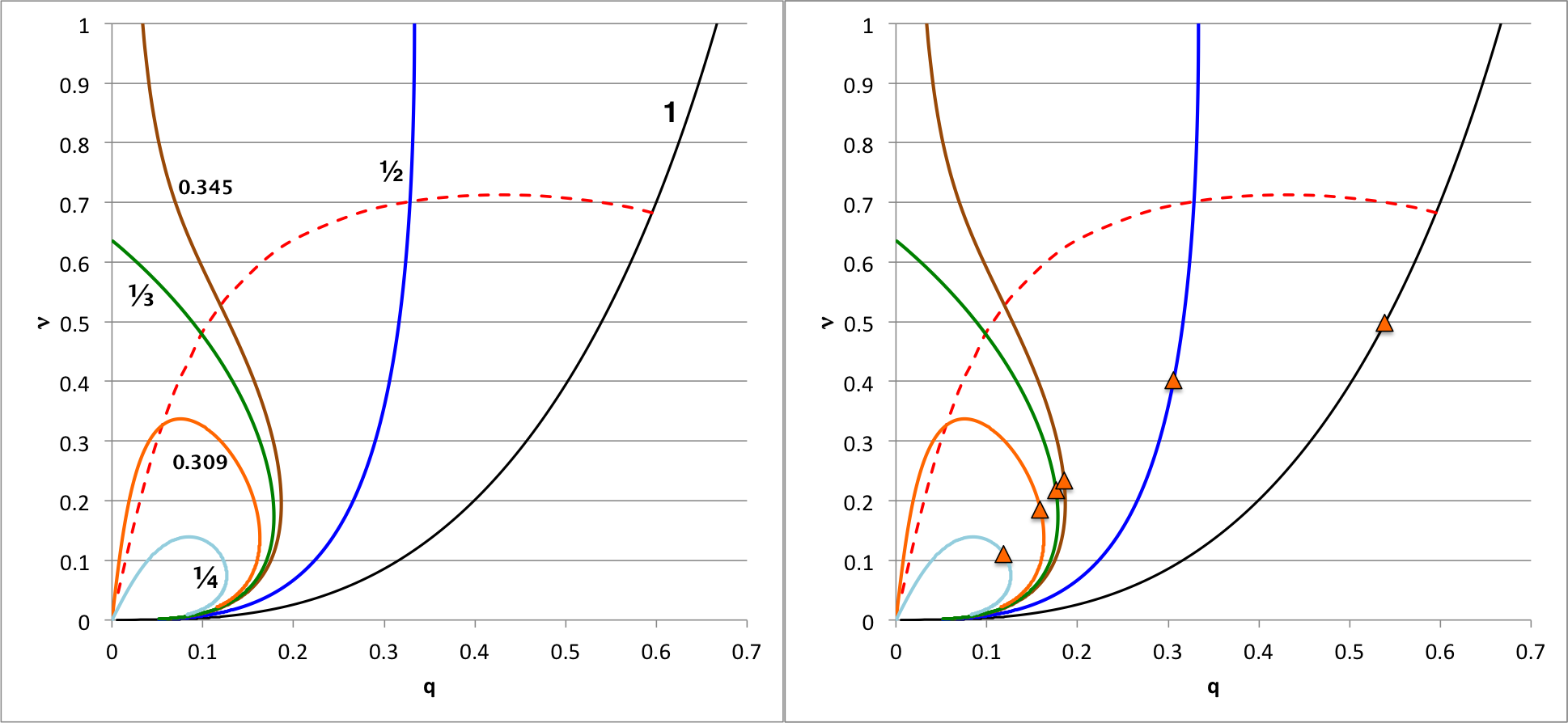 |
|||||||||
Eigenfunction Details
Here we examine some of the properties of the fundamental-mode eigenfunctions that we have found are associated with marginally unstable, <math>~(n_c, n_e) = (5,1)</math> bipolytropes.
| Figure 5 |
|---|
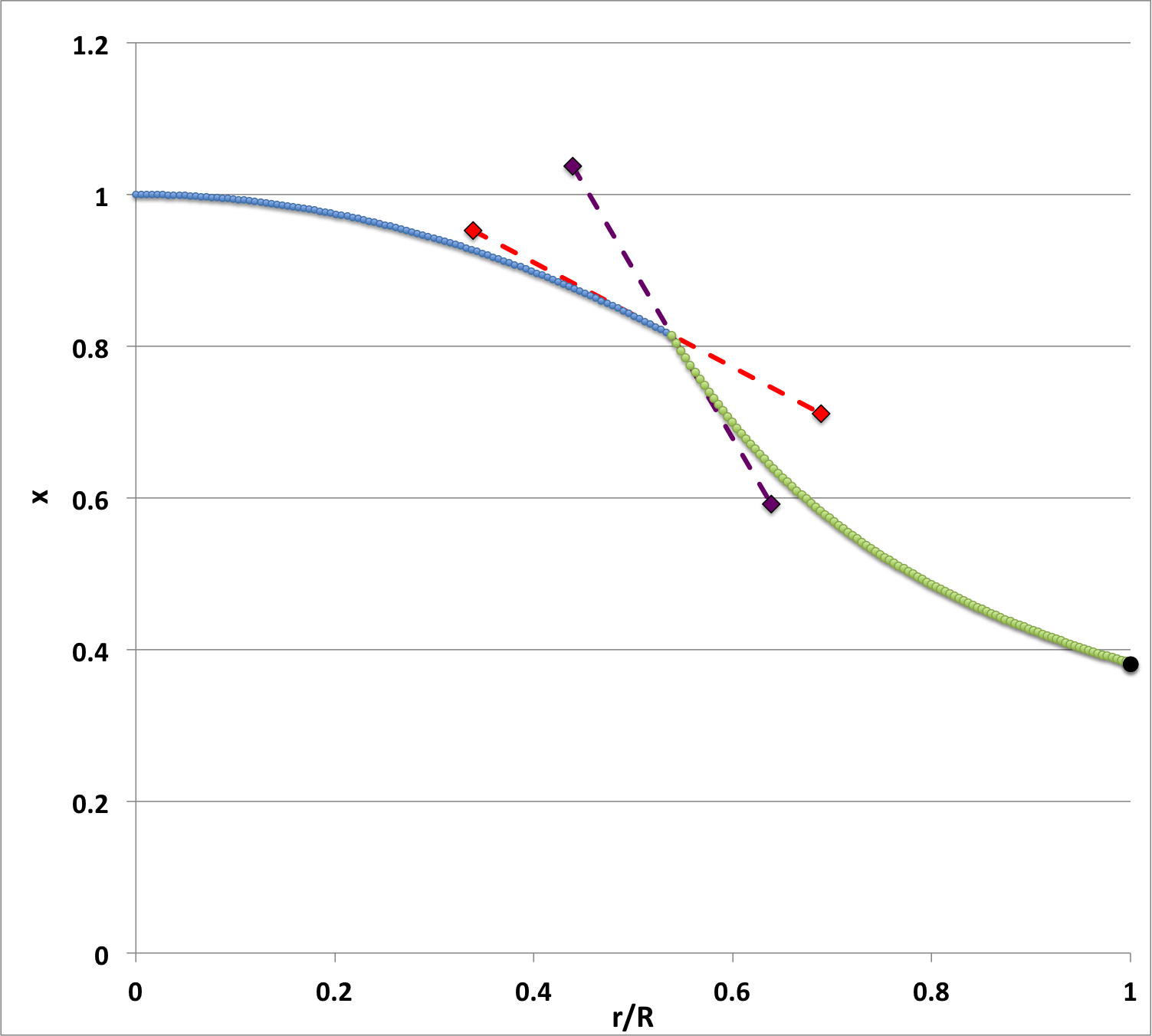
Consider the model on the <math>~\mu_e/\mu_c = 1</math> sequence for which <math>~\sigma_c^2=0~</math>; key properties of this specific equilibrium model are enumerated in the first row of numbers provided in Table 2, above. Figure 5 shows how our numerically derived, fundamental-mode eigenfunction, <math>~x = \delta r/r_0</math>, varies with the fractional radius over the entire range, <math>~0 \le r/R \le 1</math>. By prescription, the eigenfunction has a value of unity and a slope of zero at the center <math>~(r/R = 0)</math>. Integrating the LAWE outward from the center, through the model's core (blue curve segment), <math>~x</math> drops smoothly to the value <math>~x_i = 0.81437</math> at the interface <math>~(\xi_i = 1.6686460157 ~\Rightarrow~ q = r_\mathrm{core}/R_\mathrm{surf} = 0.53885819)</math>. Our numerical integration of the LAWE showed that, at the interface, the logarithmic slope of the core (blue) segment of the eigenfunction is,
|
<math>~ \biggl\{ \frac{d\ln x}{d\ln r}\biggr|_i \biggr\}_\mathrm{core} = \biggl\{ \frac{d\ln x}{d\ln \xi}\biggr|_i \biggr\}_\mathrm{core} </math> |
<math>~=</math> |
<math>~- 0.455872 \, .</math> |
Next, following the above discussion of matching conditions at the interface, we determined that, from the perspective of the envelope, the slope of the eigenfunction at the interface must therefore be,
|
<math>~ \biggl\{ \frac{d\ln x}{d\ln r}\biggr|_i \biggr\}_\mathrm{env} = \biggl\{ \frac{d\ln x}{d\ln \eta}\biggr|_i \biggr\}_\mathrm{env} </math> |
<math>~=</math> |
<math>~3\biggl(\frac{\gamma_c}{\gamma_e} -1\biggr) + \frac{\gamma_c}{\gamma_e} \biggl\{ \frac{d\ln x}{d\ln \xi}\biggr|_i \biggr\}_\mathrm{core} = -1.47352 \, .</math> |
Adopting this "env" slope along with the amplitude, <math>~x_i = 0.81437</math>, as the appropriate interface boundary conditions, we integrated the LAWE from the interface to the surface, obtaining the green-colored segment of the eigenfunction that is shown in Figure 5. The amplitude continued to steadily decrease, reaching a value of <math>~x_s = 0.38203</math>, at the model's surface <math>~(r/R = 1)</math>. At the surface, this envelope (green) segment of the eigenfunction exhibits a logarithmic slope that matches to eight significant digits the value that is expected from astrophysical arguments for this marginally unstable <math>~(\sigma_c^2=0)</math> model, namely,
<math>~ \frac{d\ln x}{d\ln \eta}\biggr|_s = \biggl[ \biggl( \frac{\rho_c}{\bar\rho} \biggr)\frac{\cancelto{0}{\sigma_c^2}}{2\gamma_e} - \biggl(3 - \frac{4}{\gamma_e}\biggr)\biggr] = -1 \, . </math>
|
Key Reminder: We were able to find an eigenfunction whose surface boundary condition matched the desired value — in this particular case, a logarithmic slope of negative one — to this high level of precision only by iterating many times and, at each step, fine-tuning our choice of the equilibrium model's radial interface location, <math>~\xi_i</math> before performing a numerical integration of the LAWE. |
The discontinuous jump that occurs in the slope of the eigenfunction at the interface results from our assumption that the effective adiabatic index of material in the core <math>~(\gamma_c = 6/5)</math> is different from the effective adiabatic index of the envelope material <math>~(\gamma_e = 2)</math>. In an effort to emphasize and more clearly illustrate the behavior of this fundamental-mode eigenfunction as it crosses the core/envelope interface, we have added a pair of dashed line segments to the Figure 5 plot. The red-dashed line segment touches, and is tangent to, the blue segment of the eigenfunction at the location of the core/envelope interface; it has a slope,
|
<math>~ \frac{dx}{d(r/R)}\biggr|_i = \frac{x_i}{(r_i/R)}\biggl\{ \frac{d\ln x}{d\ln r}\biggr|_i\biggr\}_\mathrm{core} </math> |
<math>~=</math> |
<math>~- 0.455872 \biggl(\frac{ 0.81437 }{ 0.53885819 }\biggr) = - 0.68895\, .</math> |
On the other hand, the purple-dashed line segment touches, and is tangent to, the green segment of the eigenfunction at the location of the core/envelope interface; it has a slope,
|
<math>~ \frac{dx}{d(r/R)}\biggr|_i = \frac{x_i}{(r_i/R)}\biggl\{ \frac{d\ln x}{d\ln r}\biggr|_i\biggr\}_\mathrm{env} </math> |
<math>~=</math> |
<math>~- 1.47352 \biggl(\frac{ 0.81437 }{ 0.53885819 }\biggr) = - 2.22691\, .</math> |
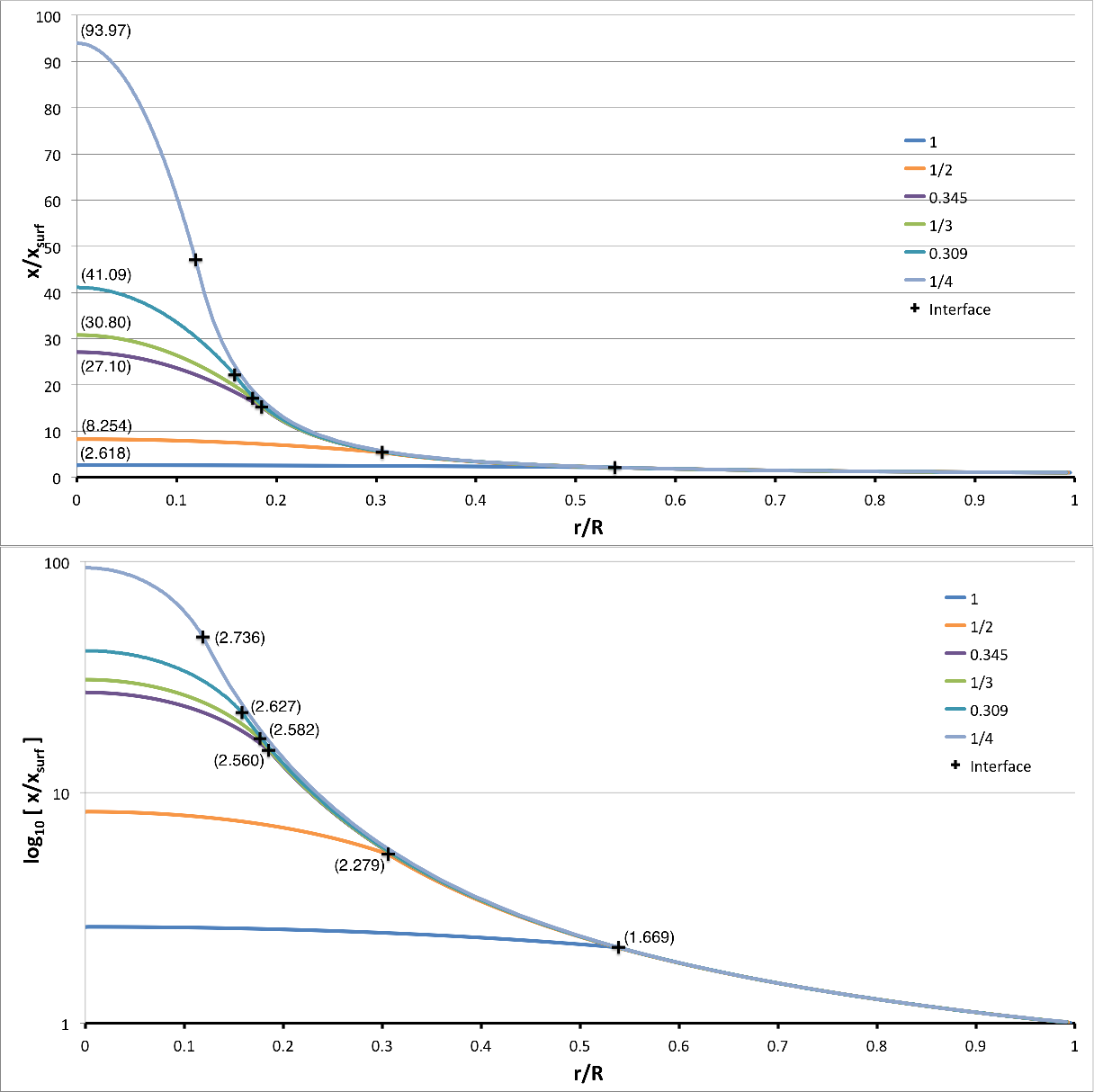
For comparison purposes, the eigenfunction shown in Figure 5 has been presented again in Figure 6, along with several other of our numerically derived eigenfunctions, but in Figure 6 the plotted amplitude has been renormalized to give a surface value — rather than a central value — of unity.
In Figure 6 we show the behavior of the fundamental-mode eigenfunction for each of the marginally unstable models identified in Table 2. In the top figure panel, each curve shows — on a linear-linear plot — how the amplitude varies with radius; in the bottom figure panel, the amplitude is plotted on a logarithmic scale. On each curve, the black plus sign marks the radial location of the core-envelope interface; in the bottom panel, these markers are accompanied by the values of <math>~\xi_i</math> that are associated with each corresponding model (see also the second column of Table 2). Each eigenfunction has been normalized such that the surface amplitude is unity. In the top panel, the value of the central amplitude of the eigenfunction that results from this normalization is recorded near the point where each eigenfunction touches the vertical axis. (In each case, the value provided on the plot is simply the inverse of the value of <math>~x_s</math> given in Table 3, below.)
|
Figure 6: Eigenfunctions Associated with the Fundamental-Mode of Radial Oscillation |
|---|
Notice that, especially as they approach the surface, the "envelope" segments of these six marginally unstable eigenfunction appear to merge into the same curve, irrespective of their value of the ratio of mean molecular weights. Note as well that the discontinuous jump that occurs in the slope of each eigenfunction at the radial location of the core/envelope interface — resulting from our choice to adopt a different adiabatic index, <math>~\gamma_g</math>, in the core from the one in the envelope — becomes less and less noticeable for smaller and smaller values of the ratio of mean molecular weights.
Is There an Analytic Expression for the Eigenfunction?
After noticing that, in Figure 6, the envelope segments of all of the marginally unstable eigenfunctions merge into the same curve, we began to wonder whether a single expression — and, even better, an analytically defined expression — would perfectly describe the eigenfunction. We had reason to believe that this might actually be possible because, in pressure-truncated polytropic configurations, we have derived analytic expressions for the marginally unstable, fundamental-mode eigenfunctions of both <math>~n = 5</math> and <math>~n=1</math> systems.
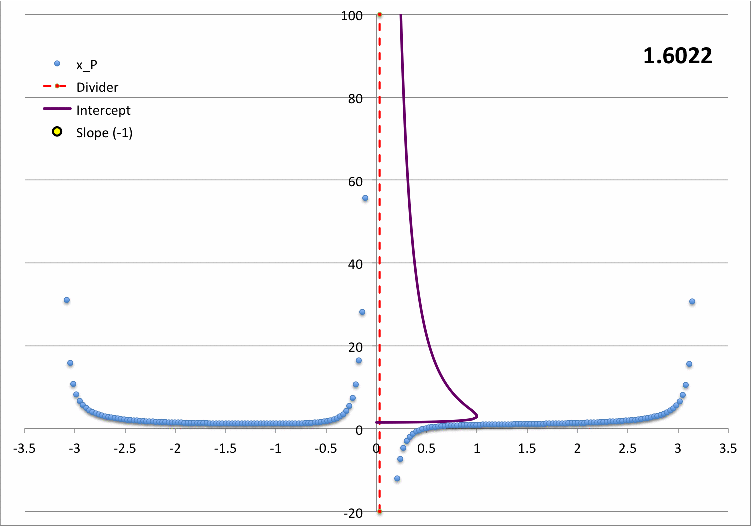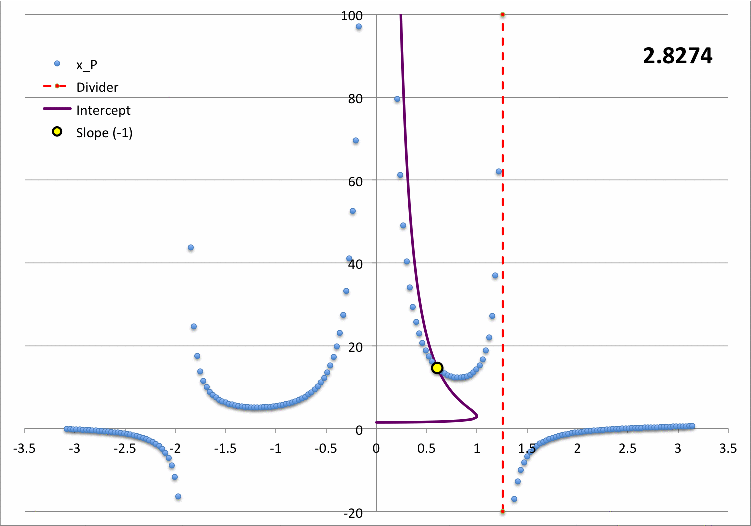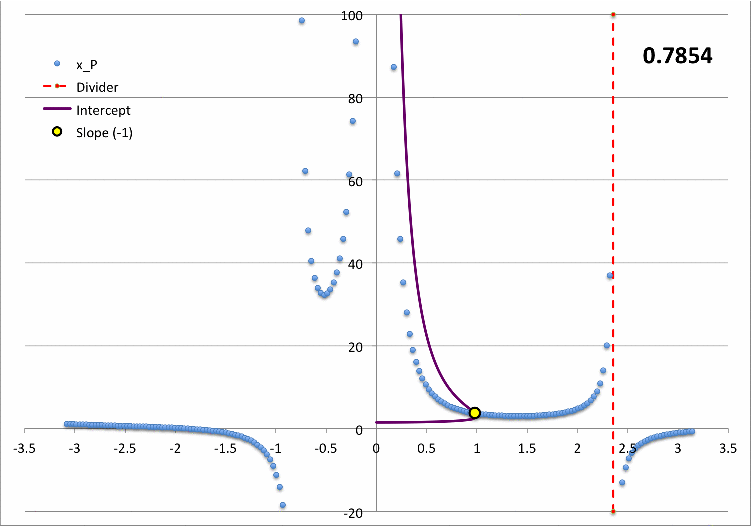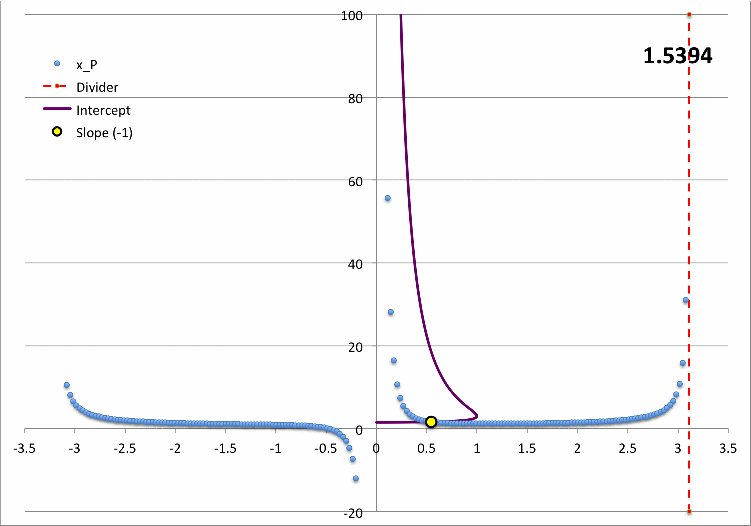
Very quickly, we convinced ourselves that a parabolic function does indeed perfectly match the "core" segment of each displayed eigenfunction. Specifically, throughout the core <math>~(0 \le \xi \le \xi_i)</math>,
|
<math>~x_P\biggr|_\mathrm{core}</math> |
<math>~\equiv</math> |
<math>~1 - \frac{\xi^2}{15}</math> |
|
<math>~\Rightarrow~~~\frac{dx_P}{d\xi}\biggr|_\mathrm{core}</math> |
<math>~\equiv</math> |
<math>~- \frac{2\xi}{15} </math> |
|
<math>~\Rightarrow~~~\frac{d\ln x_P}{d\ln \xi}\biggr|_\mathrm{core}</math> |
<math>~\equiv</math> |
<math>~- \frac{2\xi^2}{15} \biggl[ \frac{(15 - \xi^2)}{15} \biggr]^{-1} = - \frac{2\xi^2}{(15 - \xi^2)} \, .</math> |
The envelope segment posed a much greater challenge.
Attempt 1
Building on our accompanying discussion of Pressure-Truncated Configurations Having a Polytropic Index less than Three — see, for example, a relevant succinct demonstration — a promising analytic expression is,
|
<math>~x_P\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \frac{b}{\eta^2} \biggl[1 - \eta\cot(\eta - C) \biggr] \, , </math> |
where the values of the pair of coefficients, <math>~b</math> and <math>~C</math>, is to be determined. Most likely, we should set <math>~C = B</math>.
Focusing on the case of <math>~\mu_e/\mu_c = 1</math>, <math>~\gamma_c = 6/5</math>, and <math>~\gamma_e = 2</math>, here are some parameters that we think we know.
| Relevant Parameters for Marginally Unstable Model <math>~(\Omega^2 = 0)</math> with <math>~\mu_e/\mu_c = 1</math> and <math>~(\gamma_c, \gamma_e) = (\tfrac{6}{5}, 2)</math> |
||||
|---|---|---|---|---|
| <math>~\xi_i</math> | numerically determined |
<math>~\approx</math> | 1.6686460157 | |
| <math>~x_i</math> | <math>~\equiv</math> | <math>~1 - \frac{\xi_i^2}{15} </math> | <math>~=</math> | 0.814374699 |
| <math>~\biggl[\frac{d\ln x}{d\ln \xi}\biggr]_i</math> | <math>~\equiv</math> | <math>~- \frac{2\xi_i^2}{(15 - \xi_i^2)}</math> | <math>~=</math> | -0.455871976 |
| <math>~\eta_i</math> | <math>~\equiv</math> | <math>~\biggl(\frac{\mu_e}{\mu_c}\biggr) \sqrt{3} \xi_i \biggl[1 + \frac{\xi_i^2}{3}\biggr]^{-1 } </math> | <math>~=</math> | 1.498957494 |
| <math>~B</math> | <math>~\equiv</math> | <math>~\eta_i - \frac{\pi}{2} + \tan^{-1}\biggl[ \frac{1}{\eta_i} - \frac{\xi_i}{\sqrt{3}} \biggr] </math> | <math>~=</math> | - 0.359863579 |
| <math>~\eta_s</math> | <math>~\equiv</math> | <math>~\pi + B </math> | <math>~=</math> | 2.781729075 |
| <math>~\biggl[\frac{d\ln x}{d\ln \eta}\biggr]_i</math> | <math>~\equiv</math> | <math>~3\biggl( \frac{\gamma_c}{\gamma_e}-1\biggr) + \frac{\gamma_c}{\gamma_e} \biggl[\frac{d\ln x}{d\ln \xi}\biggr]_i</math> | <math>~=</math> | -1.473523186 |
| <math>~\alpha_e</math> | <math>~\equiv</math> | <math>~3 - \frac{4}{\gamma_e} </math> | <math>~=</math> | + 1 |
| <math>~\biggl[\frac{d\ln x}{d\ln \eta}\biggr]_\mathrm{surf}</math> | <math>~\equiv</math> | <math>~\frac{\cancelto{0}{\Omega^2}}{\gamma_e} - \alpha_e </math> | <math>~=</math> | - 1 |
| <math>~b</math> | <math>~\equiv</math> | <math>~\frac{3}{5}\biggl(\frac{\mu_e}{\mu_c}\biggr) \biggl[\frac{15-\xi_i^2}{3+\xi_i^2}\biggr]</math> | <math>~=</math> | 1.26097406 |
Notice that,
|
<math>~\cot(\eta_i - B)</math> |
<math>~=</math> |
<math>~\tan\biggl[ \frac{\pi}{2} -(\eta_i - B ) \biggr]</math> |
<math>~=</math> |
<math>~\biggl[ \frac{1}{\eta_i} - \frac{\xi_i}{\sqrt{3}} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \eta_i \cot(\eta_i - B)</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \frac{\xi_i \eta_i}{\sqrt{3}} \biggr] </math> |
||
|
|
<math>~=</math> |
<math>~1 - \xi_i^2 \biggl(\frac{\mu_e}{\mu_c}\biggr) \biggl[1 + \frac{\xi_i^2}{3}\biggr]^{-1 } </math> |
||
|
|
<math>~=</math> |
<math>~1 - \biggl(\frac{\mu_e}{\mu_c}\biggr) \biggl[\frac{3\xi_i^2 }{3 + \xi_i^2}\biggr] \, .</math> |
||
So if we adopt the expression for <math>~x_P</math> as given above (with C = B), then we can evaluate the leading b factor by examining the function at the interface, that is,
|
<math>~b</math> |
<math>~=</math> |
<math>~ x_i \eta_i^2 \biggl[1 - \eta_i \cot(\eta_i - B) \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ x_i \eta_i^2 \biggl[\frac{\xi_i \eta_i }{\sqrt{3}} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \eta_i \biggl[\frac{\sqrt{3}}{\xi_i} \biggr]x_i </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{\mu_e}{\mu_c}\biggr) \sqrt{3} \xi_i \biggl[1 + \frac{\xi_i^2}{3}\biggr]^{-1 } \biggl[\frac{\sqrt{3}}{\xi_i} \biggr] \biggl[1 - \frac{\xi_i^2}{15} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 3\biggl(\frac{\mu_e}{\mu_c}\biggr) \biggl[\frac{3}{3+\xi_i^2}\biggr]\biggl[\frac{15-\xi_i^2}{15} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{5}\biggl(\frac{\mu_e}{\mu_c}\biggr) \biggl[\frac{15-\xi_i^2}{3+\xi_i^2}\biggr] \, . </math> |
| Figure 7: Analytic Trial |
|---|
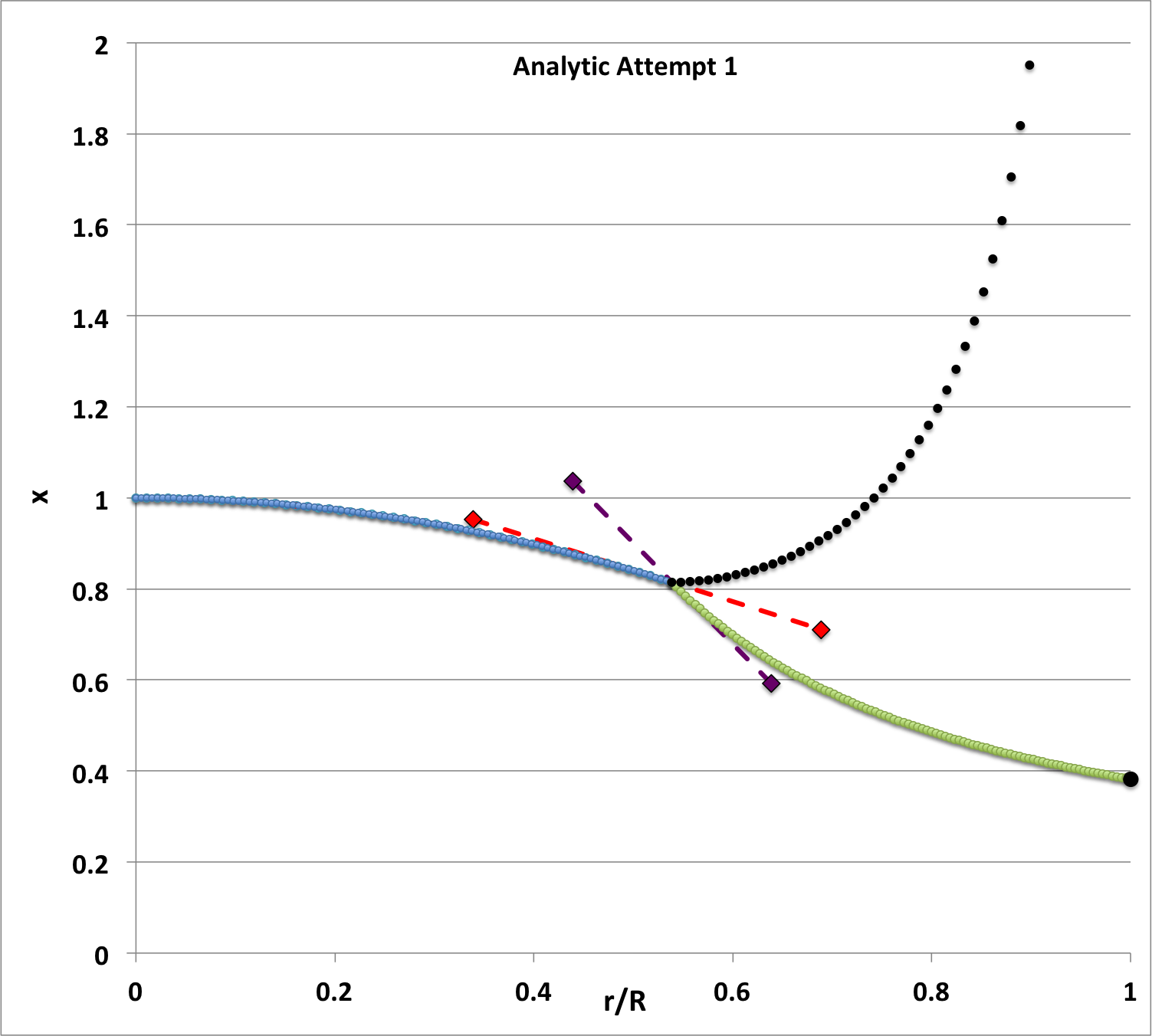 |
An even clearer way of looking at this is to realize that, quite generally,
|
<math>~(\eta - B)</math> |
<math>~=</math> |
<math>~\eta - \eta_i + \frac{\pi}{2} - \tan^{-1} f \, ,</math> |
where,
|
<math>~f</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\eta_i} - \frac{\xi_i}{\sqrt{3}} \, .</math> |
Hence, we can write,
|
<math>~\cot(\eta - B)</math> |
<math>~=</math> |
<math>~\tan\biggl[ \frac{\pi}{2} - (\eta - B) \biggr]</math> |
|
|
<math>~=</math> |
<math>~\tan\biggl[ (\eta_i - \eta) + \tan^{-1}f \biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{\tan(\eta_i - \eta) + f}{1 - f\tan(\eta_i - \eta)} \, .</math> |
As a result, we can rewrite the expression for our guess of the envelope segment of the eigenfunction in the form,
|
<math>~x_P\biggr|_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \frac{b}{\eta^2} \biggl\{ 1 - \eta \biggl[ \frac{\tan(\eta_i - \eta) + f}{1 - f\tan(\eta_i - \eta)} \biggr] \biggr\} \, . </math> |
This blows up when <math>\eta \rightarrow \eta_s</math> because, as it turns out, <math>~f = 1/\tan(\eta_i - \eta_s)</math>. We should point out, as well, that the expression for b can be rewritten in the form,
|
<math>~b</math> |
<math>~=</math> |
<math>~ \frac{\eta_i^2 (x_P)_i}{(1 - \eta_i f)} \, . </math> |
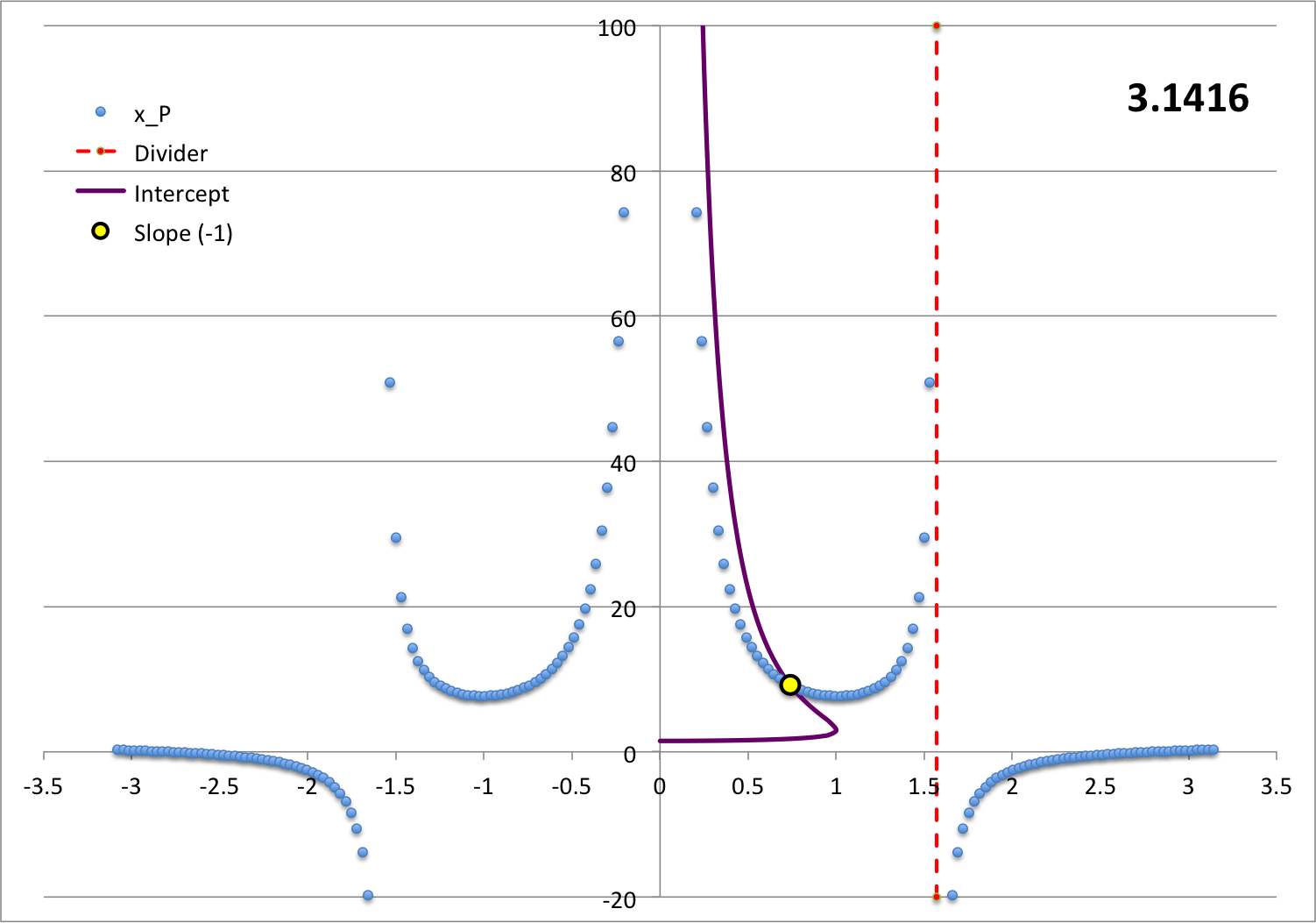
In Figure7 we have reprinted the numerically determined fundamental-mode eigenfunction that was first displayed in Figure 5, above. We have added to this plot the eigenfunction segments that are defined by our trial analytic functions: The core segment, <math>~x_P|_\mathrm{core}</math>, matches the numerically determined segment with sufficient precision that the two curve segments are indiscernible from one another. However, our analytically defined "env" segment, <math>~x_P|_\mathrm{env}</math> — identified in Figure 7 by the solid black, small circular markers — does not match the numerically determined envelope segment at all. We therefore have more work to do!
Attempt 2
Using an Excel spreadsheet as a sandbox, we employed crude, brute force iterations in an effort to fit the numerically constructed envelope eigenfunction. Here is a trial function that works pretty well. Using <math>~\eta_\mathrm{F}</math> to represent the envelope's dimensionless radial coordinate, over the range,
<math>~\eta_i \le \eta_\mathrm{F} \le \eta_s \, ,</math>
and defining the parameter,
|
<math>~g_\mathrm{F}</math> |
<math>~\equiv</math> |
<math>~ \frac{\pi}{8(\eta_s - \eta_i)} \, ,</math> |
| Limiting Parameter Values | |||
|---|---|---|---|
| min | max | <math>~\alpha = \alpha_s</math> | |
| <math>~\eta_\mathrm{F}</math> | <math>~\eta_i</math> | <math>~\eta_s</math> | <math>~\frac{8}{\pi} ( \eta_s - \eta_i )^2 + 2\eta_s - \eta_i</math> |
| <math>~\alpha</math> | <math>~-\frac{\pi}{2}</math> | <math>~-\frac{5\pi}{8}</math> | <math>~\eta_i - \eta_s - \frac{3\pi}{4}</math> |
| <math>~\Lambda</math> | <math>~\eta_i - \frac{\pi}{4}</math> | <math>~\eta_i - \frac{\pi}{8}</math> | <math>~\eta_s</math> |
we propose,
|
<math>~x_\mathrm{trial}</math> |
<math>~=</math> |
<math>~ \frac{b_0}{\Lambda^2} \biggl\{ 1 - \Lambda \biggl[ \frac{\tan(\alpha) + f_\alpha}{1 - f_\alpha \cdot \tan(\alpha)} \biggr] \biggr\} - a_0 \, , </math> |
where,
|
<math>~\frac{1}{f_\alpha} = \tan(\alpha_s)</math> |
<math>~\equiv</math> |
<math>~ \tan[ - (\eta_s - \eta_i + \tfrac{3\pi}{4}) ] \, ,</math> |
|
<math>~\alpha(\eta_\mathrm{F})</math> |
<math>~\equiv</math> |
<math>~g_\mathrm{F} \biggl[ 5\eta_i - 4\eta_s - \eta_\mathrm{F}\biggr] \, ,</math> |
|
<math>~\Lambda(\eta_\mathrm{F})</math> |
<math>~\equiv</math> |
<math>~ \eta_i + g_\mathrm{F} \biggl[ \eta_i - 2\eta_s + \eta_\mathrm{F} \biggr] \, .</math> |
| Figure 8: Another Analytic Trial |
|---|
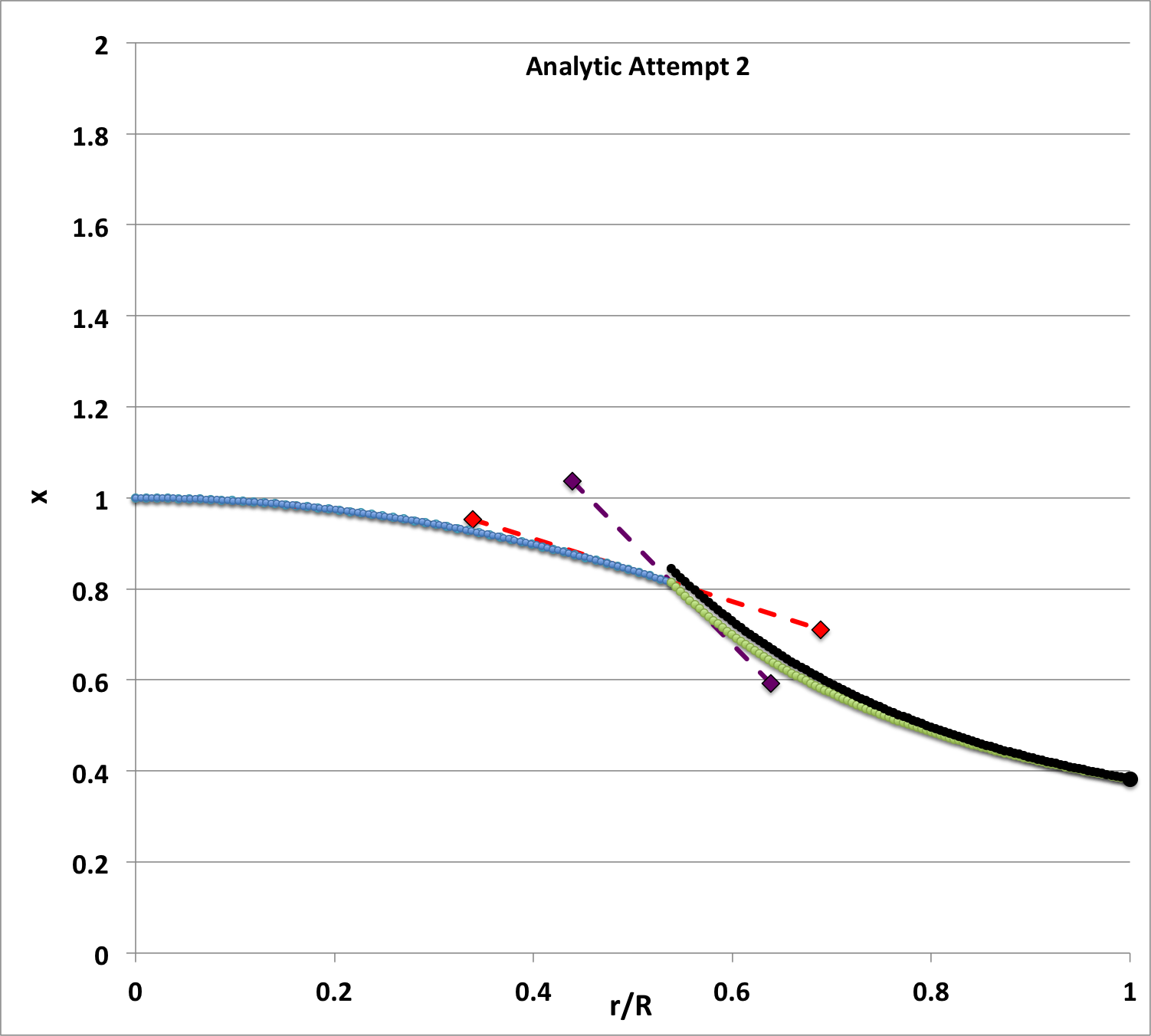 |
This function, <math>~x_\mathrm{trial}</math>, is displayed as the black-dotted curve segment in Figure 8 with the tuning/scaling parameters set to the values, <math>~(a_0, b_0) = (0.31, 0.96)</math>. We should point out that, when plotting this curve segment in Figure 8, the dimensionless radial coordinate has been defined by the relation, <math>~r^*/R^* = \eta_F/\eta_s</math>.
[16 February 2019: Comment by Tohline] When assessed visually, this trial function appears to match pretty well the numerically derived eigenfunction for the envelope. We have not yet critically assessed whether or not the function satisfies the LAWE or whether it satisfies either one (or both) of the required boundary values. This work is still to be done.
A couple of days after inserting this Comment, we recognized for the first time that, quite generally,
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~\eta_i - \biggl(\Lambda + \frac{3\pi}{4} \biggr) \, .</math> |
Hence, the parameter, <math>~\alpha</math>, can be straightforwardly removed from the expression for the trial eigenfunction to give,
|
<math>~x_\mathrm{trial}</math> |
<math>~=</math> |
<math>~ \frac{b_0}{\Lambda^2} \biggl\{ 1 - \Lambda \biggl[ \frac{\tan(\eta_i - \Lambda - 3\pi/4) + f_\alpha}{1 - f_\alpha \cdot \tan(\eta_i - \Lambda - 3\pi/4)} \biggr] \biggr\} - a_0 \, . </math> |
Drawing from our accompanying discussion of pressure-truncated polytropes, we need the eigenfunction to satisfy the,
Polytropic LAWE (linear adiabatic wave equation)
|
<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math> |
|
|
where: <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math> <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math> |
|
(Note that, in order to bring the notation of this Key Equation in line with the notation used elsewhere in this chapter, we will hereafter adopt the variable mapping <math>~\xi \rightarrow \eta</math> and <math>~\theta \rightarrow \phi</math>.) Here we are especially focused on finding a solution in the case where <math>~\sigma_c^2 = 0</math> and <math>~n = 1</math>, that is — see also our above discussion — the relevant envelope LAWE is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{d\eta^2} + \biggl[ 2 - Q \biggr] \frac{2}{\eta}\cdot \frac{dx}{d\eta} -2\alpha_g Q \cdot \frac{x}{\eta^2} \, , </math> |
where, drawing from our discussion of the n = 1 envelope's equilibrium structure,
|
<math>~Q</math> |
<math>~=</math> |
<math>~\biggl[ - \frac{d\ln\phi}{d\ln\eta} \biggr]_\mathrm{n=1} = - \frac{\eta}{\phi}\biggl[ \frac{d\phi}{d\eta} \biggr]_\mathrm{n=1}</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{1}{\sin(\eta - B)} \biggr]\biggl[ \eta\cos(\eta-B) - \sin(\eta-B) \biggr]</math> |
<math>~=</math> |
<math>~\biggl[1 - \eta\cot(\eta-B) \biggr] \, .</math> |
In an accompanying discussion — see also a short summary of the same — we have shown that an analytically specified displacement function that precisely satisfies this LAWE for pressure-truncated configurations (i.e., when B = 0) is,
|
<math>~x_P\biggr|_{n=1}</math> |
<math>~=</math> |
<math>~ \frac{3}{\eta^2}\biggl[ 1- \eta \cot\eta \biggr] \, . </math> |
In still another related discussion, we have attempted to construct an analytic eigenfunction expression that satisfies the LAWE when <math>~B \ne 0</math>.
Attempt 3
Straightforward Trial
Let's adopt a trial eigenfunction of the form
|
<math>~x_\mathrm{trial}</math> |
<math>~=</math> |
<math>~ \frac{b_0}{\Lambda^2} \biggl[ 1 - \Lambda \cot(\Lambda - E) \biggr] - a_0 \, , </math> |
where,
|
<math>~\Lambda</math> |
<math>~=</math> |
<math>~\Lambda_0 + g_\mathrm{F} \eta \, .</math> |
|
NOTE: We can retrieve the empirical expression for <math>~x_\mathrm{trial}</math> obtained above in Attempt 2 if we eventually set,
The last of these expressions arises because,
|
Because the LAWE requires derivatives of <math>~x_\mathrm{trial}</math> with respect to <math>~\eta</math>, we will often need to recognize that,
|
<math>~\frac{d}{d\eta}</math> |
<math>~=</math> |
<math>~\frac{d\Lambda}{d\eta} \cdot \frac{d}{d\Lambda} = g_\mathrm{F} \cdot \frac{d}{d\Lambda} \, .</math> |
Hence, in particular,
|
<math>~\frac{d}{d\eta}\biggl[\cot(\Lambda - E) \biggr]</math> |
<math>~=</math> |
<math>~- g_\mathrm{F} [1 + \cot^2(\Lambda - E) ] \, .</math> |
The first derivative gives,
|
<math>~\frac{d}{d\eta}\biggl[ x_\mathrm{trial} \biggr]</math> |
<math>~=</math> |
<math>~ \frac{d}{d\eta} \biggl\{ \frac{b_0}{\Lambda^2} \biggl[ 1 - \Lambda \cot(\Lambda - E) \biggr] - a_0 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~\frac{2b_0 g_\mathrm{F}}{\Lambda^3} \biggl[1 - \Lambda \cot(\Lambda - E)\biggr] + \frac{b_0}{\Lambda^2} \biggl[- g_\mathrm{F} \cot(\Lambda - E)\biggr] + \frac{b_0}{\Lambda^2} \biggl[g_\mathrm{F} \Lambda [1 + \cot^2(\Lambda - E) ] \biggr] </math> |
|
|
<math>~=</math> |
<math>~ g_\mathrm{F} b_0 \biggl\{ -~\frac{2}{\Lambda^3} \biggl[1 - \Lambda \cot(\Lambda - E)\biggr] - \frac{1}{\Lambda^2} \biggl[\cot(\Lambda - E)\biggr] + \frac{1}{\Lambda} \biggl[1 + \cot^2(\Lambda - E) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ g_\mathrm{F} b_0 \biggl\{ \frac{1}{\Lambda} -\frac{2}{\Lambda^3} +\frac{1}{\Lambda^2} \biggl[\cot(\Lambda - E)\biggr] + \frac{1}{\Lambda} \biggl[\cot^2(\Lambda - E) \biggr] \biggr\} \, . </math> |
The second derivative gives,
|
<math>~\frac{1}{g_\mathrm{F}b_0} \cdot \frac{d^2}{d\eta^2}\biggl[ x_\mathrm{trial} \biggr]</math> |
<math>~=</math> |
<math>~\frac{d}{d\eta}\biggl\{ \frac{1}{\Lambda} -\frac{2}{\Lambda^3} +\frac{1}{\Lambda^2} \biggl[\cot(\Lambda - E)\biggr] + \frac{1}{\Lambda} \biggl[\cot^2(\Lambda - E) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{g_\mathrm{F}}{\Lambda^2} +\frac{6 g_\mathrm{F}}{\Lambda^4} -\frac{2g_\mathrm{F}}{\Lambda^3} \biggl[\cot(\Lambda - E)\biggr] - \frac{g_\mathrm{F}}{\Lambda^2} \biggl[1 + \cot^2(\Lambda - E)\biggr] </math> |
|
|
|
<math>~ - \frac{g_\mathrm{F}}{\Lambda^2} \biggl[\cot^2(\Lambda - E) \biggr] - \frac{2g_\mathrm{F}}{\Lambda} \biggl[\cot(\Lambda - E) \biggr] \biggl[1 + \cot^2(\Lambda - E) \biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{1}{g^2_\mathrm{F}b_0} \cdot \frac{d^2}{d\eta^2}\biggl[ x_\mathrm{trial} \biggr]</math> |
<math>~=</math> |
<math>~ -\frac{1}{\Lambda^2} +\frac{6 }{\Lambda^4} -\frac{2}{\Lambda^3} \biggl[\cot(\Lambda - E)\biggr] - \frac{1}{\Lambda^2} - \frac{1}{\Lambda^2} \biggl[\cot^2(\Lambda - E)\biggr] </math> |
|
|
|
<math>~ - \frac{1}{\Lambda^2} \biggl[\cot^2(\Lambda - E) \biggr] - \frac{2}{\Lambda} \biggl[\cot(\Lambda - E) + \cot^3(\Lambda - E) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{\Lambda^2} - \frac{1}{\Lambda^2} +\frac{6 }{\Lambda^4} -\frac{2}{\Lambda^3} \biggl[\cot(\Lambda - E)\biggr] - \frac{2}{\Lambda} \biggl[\cot(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - \frac{1}{\Lambda^2} \biggl[\cot^2(\Lambda - E) \biggr] - \frac{1}{\Lambda^2} \biggl[\cot^2(\Lambda - E)\biggr] - \frac{2}{\Lambda} \biggl[ \cot^3(\Lambda - E) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -\frac{2}{\Lambda^2} +\frac{6 }{\Lambda^4} - \biggl[ \frac{2}{\Lambda^3} + \frac{2}{\Lambda}\biggr]\biggl[\cot(\Lambda - E)\biggr] - \frac{2}{\Lambda^2} \biggl[\cot^2(\Lambda - E) \biggr] - \frac{2}{\Lambda} \biggl[ \cot^3(\Lambda - E) \biggr] \, . </math> |
So, appreciating that, <math>~\eta = (\Lambda - \Lambda_0 )/g_\mathrm{F}</math>, and dividing the relevant LAWE through by <math>~b_0 g_\mathrm{F}^2</math>, we have,
|
<math>~\frac{1}{b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ \frac{1}{b_0 g_\mathrm{F}^2} \cdot \frac{d^2x_\mathrm{trial} }{d\eta^2} + \frac{1}{b_0 g_\mathrm{F}^2} \biggl[ 2 - Q \biggr] \frac{2g_\mathrm{F}}{(\Lambda - \Lambda_0 )}\cdot \frac{dx_\mathrm{trial}}{d\eta} - \frac{2Q}{b_0 g_\mathrm{F}^2} \cdot \frac{g^2_\mathrm{F} x_\mathrm{trial}}{(\Lambda - \Lambda_0 )^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(\Lambda - \Lambda_0 )^2} \biggl\{ \frac{(\Lambda - \Lambda_0 )^2}{b_0 g_\mathrm{F}^2} \cdot \frac{d^2x}{d\eta^2} + \frac{ (\Lambda - \Lambda_0 )}{b_0 g_\mathrm{F}} \biggl[ 2 - Q \biggr] \frac{dx}{d\eta} - \frac{2Q}{b_0 } \cdot x \biggr\} </math> |
|
<math>~\Rightarrow~~~ \frac{ (\Lambda - \Lambda_0 )^2}{b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 )^2 \biggl\{ \frac{1}{b_0 g_\mathrm{F}^2} \cdot \frac{d^2x}{d\eta^2} \biggr\} + (\Lambda - \Lambda_0 ) \biggl[ 4 - 2Q \biggr] \biggl\{ \frac{1}{b_0 g_\mathrm{F}} \frac{dx}{d\eta} \biggr\} - 2Q \biggl\{ \frac{x}{b_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 )^2 \biggl\{ -\frac{2}{\Lambda^2} +\frac{6 }{\Lambda^4} - \biggl[ \frac{2}{\Lambda^3} + \frac{2}{\Lambda}\biggr]\biggl[\cot(\Lambda - E)\biggr] - \frac{2}{\Lambda^2} \biggl[\cot^2(\Lambda - E) \biggr] - \frac{2}{\Lambda} \biggl[ \cot^3(\Lambda - E) \biggr] \biggr\} </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0 ) \biggl[ 4 - 2Q \biggr] \biggl\{ \frac{1}{\Lambda} -\frac{2}{\Lambda^3} +\frac{1}{\Lambda^2} \biggl[\cot(\Lambda - E)\biggr] + \frac{1}{\Lambda} \biggl[\cot^2(\Lambda - E) \biggr] \biggr\} </math> |
|
|
|
<math>~ - 2Q \biggl\{ \frac{1}{\Lambda^2} \biggl[1 - \Lambda \cot(\Lambda - E) \biggr] - \frac{ a_0 }{b_0} \biggr\} </math> |
|
<math>~\Rightarrow~~~ \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 )^2 \biggl\{ (6-2\Lambda^2) - (2\Lambda + 2\Lambda^3 ) \cot(\Lambda - E) - 2\Lambda^2 \cot^2(\Lambda - E) - 2\Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0 ) (4 - 2Q ) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2 \cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - 2Q \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
<math>~\Rightarrow~~~ \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2)(\Lambda - \Lambda_0 ) - (\Lambda + \Lambda^3 )(\Lambda - \Lambda_0 ) \cot(\Lambda - E) - \Lambda^2 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) - \Lambda^3 (\Lambda - \Lambda_0 )\cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0 ) \biggl\{ 2\Lambda^3 -4\Lambda +2\Lambda^2 \cot(\Lambda - E) + 2\Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -Q \biggl\{ \Lambda^3(\Lambda - \Lambda_0 ) -2\Lambda (\Lambda - \Lambda_0 ) +\Lambda^2 (\Lambda - \Lambda_0 )\cot(\Lambda - E) + \Lambda^3 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - Q \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} \, . </math> |
The right-hand-side of this expression should simplify considerably if we let <math>~E \rightarrow B</math>, if we set <math>~(g_\mathrm{F}, \Lambda_0) = (1, 0) ~\Rightarrow~ \Lambda = \eta</math>, and if <math>~(a_0, b_0) = (0, 3)</math>. Let's see.
|
RHS |
<math>~=</math> |
<math>~ \Lambda \biggl\{ (3-\Lambda^2)\Lambda - (\Lambda + \Lambda^3 )\Lambda \cot(\Lambda - E) - \Lambda^3 \cot^2(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) +2\Lambda^3 -4\Lambda +2\Lambda^2 \cot(\Lambda - E) + 2\Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -Q \biggl\{ \Lambda^4 -2\Lambda^2 +\Lambda^3 \cot(\Lambda - E) + \Lambda^4 \cot^2(\Lambda - E) +\Lambda^2 - \Lambda^3 \cot(\Lambda - E) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \Lambda \biggl\{ (-\Lambda +\Lambda^3) + (\Lambda^2 - \Lambda^4) \cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) -\Lambda^3 + \Lambda - \Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ +\Lambda\cot(\lambda-E) \biggl\{ \Lambda^4 -2\Lambda^2 +\Lambda^3 \cot(\Lambda - E) + \Lambda^4 \cot^2(\Lambda - E) +\Lambda^2 - \Lambda^3 \cot(\Lambda - E) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \Lambda \biggl\{ (\Lambda^2 - \Lambda^4) \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr\} +\Lambda\cot(\lambda-E) \biggl\{ \Lambda^4 -\Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
EXCELLENT !!
Let's return to the more general expression and see if it can be simplified.
|
<math>~ \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ \Lambda (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - \Lambda_0 (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + \Lambda (\Lambda - \Lambda_0 ) \biggl\{ 2\Lambda^2 -4 +2\Lambda \cot(\Lambda - E) + 2\Lambda^2 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -Q(\Lambda - \Lambda_0 ) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} - Q \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \Lambda (\Lambda - \Lambda_0 ) \biggl\{ (\Lambda^2-1) + (\Lambda - \Lambda^3 ) \cot(\Lambda - E) + \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} - \Lambda (\Lambda - \Lambda_0 ) \biggl\{ \Lambda^2 -2 +\Lambda \cot(\Lambda - E) + \Lambda^2 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - \Lambda_0 (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} - \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) (\Lambda - \Lambda_0 ) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} + \eta\cot(\eta-B) \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \Lambda (\Lambda - \Lambda_0 ) \biggl\{ 1 - \Lambda^3 \cot(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - \Lambda_0 (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} - \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) (\Lambda - \Lambda_0 ) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} + \eta\cot(\eta-B) \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
Simplifying again produces,
|
RHS |
<math>~=</math> |
<math>~ \Lambda^2 \biggl\{ 1 - \Lambda^3 \cot(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} - \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + \Lambda^2 \cot(\Lambda-E) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} + \Lambda \cot(\Lambda-E) \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \Lambda^3 \cot(\Lambda - E) - \Lambda^5 \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) </math> |
|
|
|
<math>~ +\Lambda^5 \cot(\Lambda-E) - 2\Lambda^3 \cot(\Lambda-E) +\Lambda^4\cot^2(\Lambda - E) + \Lambda^5 \cot^3(\Lambda - E) + \Lambda^3 \cot(\Lambda-E) - \Lambda^4 \cot^2(\Lambda - E) </math> |
|
|
<math>~=</math> |
<math>~ 0\, . </math> |
EXCELLENT !! Keep trying to simplify the more general expression …
|
<math>~ \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ \biggl\{ \Lambda^2 - \Lambda^5 \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) - \Lambda^2 + \Lambda^3 \cot(\Lambda - E) + \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} - \Lambda_0 \biggl\{ \Lambda - \Lambda^4 \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - \Lambda_0 (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) (\Lambda ) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} + \eta\cot(\eta-B) \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
|
<math>~ - \eta\cot(\eta-B) (\Lambda_0) \biggl\{ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \Lambda^2 - \Lambda^5 \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) - \Lambda^2 + \Lambda^3 \cot(\Lambda - E) + \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr] </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) \biggl[ \Lambda^4 -2\Lambda^2 +\Lambda^3 \cot(\Lambda - E) + \Lambda^4 \cot^2(\Lambda - E) + \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr] </math> |
|
|
|
<math>~ - \Lambda_0 \biggl\{ (\Lambda - \Lambda_0 ) \biggl[ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr] + \biggl[ \Lambda - \Lambda^4 \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) \biggl[ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 + (\Lambda^3 - \Lambda^5) \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) \biggr] + \eta\cot(\eta-B) \biggl[ \biggl(1- \frac{ a_0 }{b_0}\biggr)\Lambda^4 - \Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - \Lambda_0 \biggl\{ (\Lambda - \Lambda_0 ) \biggl[ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr] + \biggl[ \Lambda - \Lambda^4 \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + \eta\cot(\eta-B) \biggl[ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr] \biggr\} \, . </math> |
Simplify again …
|
RHS |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 + (\Lambda^3 - \Lambda^5) \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) \biggr] + \eta\cot(\eta-B) \biggl[ \biggl(1- \frac{ a_0 }{b_0}\biggr)\Lambda^4 - \Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 + (\Lambda^3 - \Lambda^5) \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) \biggr] + \biggl[ (\Lambda^5 - \Lambda^3) \cot(\Lambda-E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^5\cot(\Lambda-E) + \Lambda^5 \cot^3(\Lambda - E) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{ a_0 }{b_0}\biggr) \biggl[ \Lambda^4 - \Lambda^5\cot(\Lambda-E)\biggr] \, . </math> |
First Argument Relationships Guess
Let's try the relationship,
|
<math>~(\eta - B)</math> |
<math>~=</math> |
<math>~m(\Lambda - E) \, .</math> |
Then, for example, if <math>~m = 2</math>, we can make the replacement,
<math>~\cot(\eta - B) = \cot[2(\Lambda - E)] = \frac{\cot^2(\Lambda - E) - 1}{2\cot(\Lambda - E)} \, .</math>
And, alternatively, if <math>~m = 3</math>, we can make the replacement,
<math>~\cot(\eta - B) = \cot[3(\Lambda - E)] = \frac{\cot^3(\Lambda - E) - 3\cot(\Lambda - E)}{3\cot^2(\Lambda - E)-1} \, .</math>
|
IMPLICATIONS
Given that we also are assuming the relationship,
we have,
In order for this statement to be true for all <math>~\Lambda</math>, the RHS and the LHS must independently be zero. Hence, we require, <math>~g_\mathrm{F} = \frac{1}{m}</math> and <math>~\Lambda_0 = E - \frac{B}{m} \, .</math> |
Let's try <math>~m=2</math>:
|
<math>~ 2\cot(\Lambda - E) \cdot \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ 2\cot(\Lambda - E)\biggl[ \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 + (\Lambda^3 - \Lambda^5) \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + 2(\Lambda - \Lambda_0) [\cot^2(\Lambda - E) - 1]\biggl[ \biggl(1- \frac{ a_0 }{b_0}\biggr)\Lambda^4 - \Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - \Lambda_0 \biggl\{ 2(\Lambda - \Lambda_0 )\cot(\Lambda - E) \biggl[ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + 2(\Lambda - \Lambda_0)[\cot^2(\Lambda - E) - 1] \biggl[ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + 2\cot(\Lambda - E)\biggl[ \Lambda - \Lambda^4 \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr] \biggr\} </math> |
|
<math>~ \Rightarrow ~~~\cot(\Lambda - E) \cdot \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ </math> |
|
|
|
<math>~ + \Lambda_0 (\Lambda - \Lambda_0) \biggl[ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - (\Lambda - \Lambda_0) \biggl[ \biggl(1- \frac{ a_0 }{b_0}\biggr)\Lambda^4 - \Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ \cot(\Lambda - E)\biggl[ \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 + (\Lambda^3 - \Lambda^5) \cot(\Lambda - E) - \Lambda^5 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ -\Lambda_0 (\Lambda - \Lambda_0 )\cot(\Lambda - E) \biggl[ (3-\Lambda^2) - (\Lambda + \Lambda^3 ) \cot(\Lambda - E) - \Lambda^2 \cot^2(\Lambda - E) - \Lambda^3 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - \Lambda_0 \cot(\Lambda - E)\biggl[ \Lambda - \Lambda^4 \cot(\Lambda - E) - \Lambda^4 \cot^3(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0) \cot^2(\Lambda - E) \biggl[ \biggl(1- \frac{ a_0 }{b_0}\biggr)\Lambda^4 - \Lambda^2 + \Lambda^4 \cot^2(\Lambda - E) \biggr] </math> |
|
|
|
<math>~ - \Lambda_0 (\Lambda - \Lambda_0)\cot^2(\Lambda - E) \biggl[ \Lambda^3 -2\Lambda +\Lambda^2\cot(\Lambda - E) + \Lambda^3 \cot^2(\Lambda - E) \biggr] </math> |
Second Argument Relationships Guess
Let's go back up to the general expression,
|
<math>~\Rightarrow~~~ \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2)(\Lambda - \Lambda_0 ) - (\Lambda + \Lambda^3 )(\Lambda - \Lambda_0 ) \cot(\Lambda - E) - \Lambda^2 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) - \Lambda^3 (\Lambda - \Lambda_0 )\cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0 ) \biggl\{ 2\Lambda^3 -4\Lambda +2\Lambda^2 \cot(\Lambda - E) + 2\Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -Q \biggl\{ \Lambda^3(\Lambda - \Lambda_0 ) -2\Lambda (\Lambda - \Lambda_0 ) +\Lambda^2 (\Lambda - \Lambda_0 )\cot(\Lambda - E) + \Lambda^3 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - Q \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} \, , </math> |
where,
|
<math>~Q</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \eta \cot(\eta - B) \biggr] \, .</math> |
|
|
<math>~=</math> |
<math>~1 - \biggl[\frac{(\Lambda - \Lambda_0)}{g_\mathrm{F}}\biggr] \cot[ (\Lambda - \Lambda_0)/g_\mathrm{F} - B] \, . </math> |
Then, let's try setting,
|
<math>~\cot[ (\Lambda - \Lambda_0)/g_\mathrm{F} - B]</math> |
<math>~=</math> |
<math>~\tan(\Lambda - E)</math> |
|
<math>~\Rightarrow ~~~ \cot\biggl\{ \frac{\pi}{2} - \biggl[ \frac{\pi}{2} + B - (\Lambda - \Lambda_0)/g_\mathrm{F} \biggr] \biggr\}</math> |
<math>~=</math> |
<math>~\tan(\Lambda - E)</math> |
|
<math>~\Rightarrow ~~~ \frac{\pi}{2} + B - \frac{ (\Lambda - \Lambda_0) }{g_\mathrm{F}} </math> |
<math>~=</math> |
<math>~\Lambda - E \, .</math> |
This will only work for all <math>~\Lambda</math> if, <math>~g_\mathrm{F} = -1</math>; in which case,
|
<math>~\frac{\pi}{2} + B + (\Lambda - \Lambda_0) </math> |
<math>~=</math> |
<math>~\Lambda - E </math> |
|
<math>~\Rightarrow ~~~ E </math> |
<math>~=</math> |
<math>~\Lambda_0 - \frac{\pi}{2} - B \, . </math> |
Hence, we have,
|
<math>~Q</math> |
<math>~=</math> |
<math>~1 + (\Lambda - \Lambda_0)\tan(\Lambda - E) </math> |
|
<math>~\Rightarrow ~~~ Q \cot(\Lambda-E)</math> |
<math>~=</math> |
<math>~\cot(\Lambda-E) + (\Lambda - \Lambda_0) \, .</math> |
This means that,
|
<math>~\cot(\Lambda-E) \cdot \frac{ \Lambda^4(\Lambda - \Lambda_0 )^2}{2b_0 g_\mathrm{F}^2} \cdot 0</math> |
<math>~=</math> |
<math>~ \cot(\Lambda-E)(\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2)(\Lambda - \Lambda_0 ) - (\Lambda + \Lambda^3 )(\Lambda - \Lambda_0 ) \cot(\Lambda - E) - \Lambda^2 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) - \Lambda^3 (\Lambda - \Lambda_0 )\cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + \cot(\Lambda-E)(\Lambda - \Lambda_0 ) \biggl\{ 2\Lambda^3 -4\Lambda +2\Lambda^2 \cot(\Lambda - E) + 2\Lambda^3 \cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -[\cot(\Lambda-E) + (\Lambda - \Lambda_0)] \biggl\{ \Lambda^3(\Lambda - \Lambda_0 ) -2\Lambda (\Lambda - \Lambda_0 ) +\Lambda^2 (\Lambda - \Lambda_0 )\cot(\Lambda - E) + \Lambda^3 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - [\cot(\Lambda-E) + (\Lambda - \Lambda_0)] \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ (\Lambda - \Lambda_0 ) \biggl\{ (3-\Lambda^2)(\Lambda - \Lambda_0 )\cot(\Lambda-E) - (\Lambda + \Lambda^3 )(\Lambda - \Lambda_0 ) \cot^2(\Lambda - E) - \Lambda^2 (\Lambda - \Lambda_0 )\cot^3(\Lambda - E) - \Lambda^3 (\Lambda - \Lambda_0 )\cot^4(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ + (\Lambda - \Lambda_0 ) \biggl\{ 2\Lambda^3\cot(\Lambda-E) -4\Lambda \cot(\Lambda-E) +2\Lambda^2 \cot^2(\Lambda - E) + 2\Lambda^3 \cot^3(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ -(\Lambda - \Lambda_0) \biggl\{ \Lambda^3(\Lambda - \Lambda_0 ) -2\Lambda (\Lambda - \Lambda_0 ) +\Lambda^2 (\Lambda - \Lambda_0 )\cot(\Lambda - E) + \Lambda^3 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) \biggr\} </math> |
|
|
|
<math>~ - (\Lambda - \Lambda_0) \biggl\{ \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} </math> |
|
|
|
<math>~ -[\cot(\Lambda-E) ] \biggl\{ \Lambda^3(\Lambda - \Lambda_0 ) -2\Lambda (\Lambda - \Lambda_0 ) +\Lambda^2 (\Lambda - \Lambda_0 )\cot(\Lambda - E) + \Lambda^3 (\Lambda - \Lambda_0 )\cot^2(\Lambda - E) + \Lambda^2 - \Lambda^3 \cot(\Lambda - E) - \biggl( \frac{ a_0 }{b_0}\biggr)\Lambda^4 \biggr\} \, . </math> |
Attempt 4A
Try, the structural function,
|
<math>~\theta</math> |
<math>~=</math> |
<math>~\frac{1}{\xi} \biggl[A\sin\xi - B\cos\xi \biggr] </math> |
<math>~=</math> |
<math>~\frac{a_0}{\xi} \cdot \sin(\xi - b_0) \, ,</math> |
where, recognizing that, <math>~f \equiv B/A</math>,
|
<math>~a_0 \equiv A \sqrt{1 + f^2}</math> |
and |
<math>~b_0 \equiv \tan^{-1}f \, .</math> |
Does this structural function satisfy the Lane-Emden equation, namely …
|
<math>~\xi^2 \frac{d^2\theta}{d\xi^2} + 2\xi \frac{d\theta}{d\xi} + \xi^2\theta</math> |
<math>~=</math> |
<math>~0 \, .</math> |
First, recognize that,
|
<math>~\frac{d\theta}{d\xi}</math> |
<math>~=</math> |
<math>~ \frac{a_0}{\xi} \cdot \cos(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \sin(\xi - b_0) \, , </math> |
and,
|
<math>~\frac{d^2\theta}{d\xi^2}</math> |
<math>~=</math> |
<math>~ - \frac{a_0}{\xi} \cdot \sin(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \cos(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \cos(\xi - b_0) + \frac{2a_0}{\xi^3} \cdot \sin(\xi - b_0) \, . </math> |
Hence,
|
<math>~ \xi^2 \frac{d^2\theta}{d\xi^2} + 2\xi \frac{d\theta}{d\xi} + \xi^2\theta </math> |
<math>~=</math> |
<math>~ \xi^2 \biggl\{ - \frac{a_0}{\xi} \cdot \sin(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \cos(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \cos(\xi - b_0) + \frac{2a_0}{\xi^3} \cdot \sin(\xi - b_0) \biggr\} + 2\xi \biggl\{ \frac{a_0}{\xi} \cdot \cos(\xi - b_0) - \frac{a_0}{\xi^2} \cdot \sin(\xi - b_0) \biggr\} + \xi^2\biggl\{ \frac{a_0}{\xi}\cdot \sin(\xi - b_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ -a_0 \xi \cdot \sin(\xi - b_0) - 2a_0 \cdot \cos(\xi - b_0) + \frac{2a_0}{\xi} \cdot \sin(\xi - b_0) \biggr\} + \biggl\{ 2a_0\cdot \cos(\xi - b_0) - \frac{2a_0}{\xi} \cdot \sin(\xi - b_0) \biggr\} + a_0 \xi\cdot \sin(\xi - b_0) </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
Good!
Attempt 4B
Let's continue with the same 4A approach, but shift to the variable notation that we have used in the accompanying description of how to build an equilibrium, (nc, ne) = (5, 1) bipolytrope. For example, the envelope's structural function will be referred to as <math>~\phi(\eta)</math> instead of <math>~\theta(\xi)</math>. Specifically, we have,
|
<math>~\phi</math> |
<math>~=</math> |
<math>~a_0 \biggl[ \frac{\sin(\eta - b_0)}{\eta} \biggr] \, ,</math> |
and,
|
<math>~\frac{d\phi}{d\eta}</math> |
<math>~=</math> |
<math>~\frac{a_0}{\eta^2} \biggl[ \eta \cos(\eta - b_0) - \sin(\eta - b_0) \biggr] \, ,</math> |
and,
|
<math>~\frac{d^2\phi}{d\eta^2}</math> |
<math>~=</math> |
<math>~ - \frac{a_0}{\eta} \cdot \sin(\eta - b_0) - \frac{2a_0}{\eta^2} \cdot \cos(\eta - b_0) + \frac{2a_0}{\eta^3} \cdot \sin(\eta - b_0) \, . </math> |
This satisfies the Lane-Emden equation for any values of the parameter pair, <math>~a_0</math> and <math>~b_0</math>. Note that,
|
<math>~Q \equiv - \frac{d\ln \phi}{d\ln\eta}</math> |
<math>~=</math> |
<math>~\frac{a_0}{\eta^2} \biggl[\sin(\eta - b_0) - \eta \cos(\eta - b_0) \biggr] \cdot \frac{\eta}{\phi}</math> |
|
|
<math>~=</math> |
<math>~\biggl[1 - \eta \cot(\eta - b_0) \biggr] </math> |
|
<math>~\Rightarrow~~~ \eta \cot(\eta - b_0) </math> |
<math>~=</math> |
<math>~(1 - Q ) \, .</math> |
|
Note that for the <math>~\mu_e/\mu_c = 1</math> model having a core-envelope interface of <math>~\xi_i = 1.668646016</math> (and an adopted normalization, φi = 1), we also have,
Some of this is also detailed above in the Attempt 1 subsection. |
Now, guided by a separate parallel discussion, we want to see whether, in the case of a bipolytropic configuration for which <math>~n_e=1</math>, the
| Precise Solution to the Polytropic LAWE | |||
|
<math>~\sigma_c^2 = 0</math> |
and |
<math>~x_P </math> |
<math>~ \equiv \frac{3c_0 (n-1)}{2n}\biggl[1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\eta \phi^{n}}\biggr) \frac{d\phi}{d\eta}\biggr] </math> |
|
|
<math>~= -\biggl( \frac{3c_0}{\eta \phi}\biggr) \frac{d\phi}{d\eta} = \frac{3c_0}{\eta^2} \cdot Q \, , </math> |
||
satisfies the governing LAWE, namely,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x_P}{d\eta^2} + \biggl[4 - 2Q\biggr]\frac{1}{\eta}\cdot \frac{dx_P}{d\eta} - 2Q\cdot \frac{x_P}{\eta^2} \, . </math> |
Well … recognizing that,
|
<math>~\frac{d}{d\eta} \biggl[\cot(\eta - b_0)\biggr]</math> |
<math>~=</math> |
<math>~- \biggl[ 1 + \cot^2(\eta - b_0)\biggr] \, ,</math> |
we have,
|
<math>~\frac{dQ}{d\eta}</math> |
<math>~=</math> |
<math>~ \eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \, , </math> |
and,
|
<math>~\frac{d^2Q}{d\eta^2}</math> |
<math>~=</math> |
<math>~\frac{d}{d\eta}\biggl[ \eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \biggl[ 1 + \cot^2(\eta - b_0)\biggr] +\cot^2(\eta - b_0) -2\eta \cot(\eta - b_0)\biggl[ 1 + \cot^2(\eta - b_0)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2 -2\eta \cot(\eta - b_0) + 2\cot^2(\eta - b_0) -2\eta \cot^3(\eta - b_0) \, . </math> |
Hence,
|
<math>~\frac{1}{3c_0}\cdot \frac{dx_P}{d\eta}</math> |
<math>~=</math> |
<math>~\frac{1}{\eta^2} \frac{dQ}{d\eta} - \frac{2Q}{\eta^3} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\eta^2}\biggl[\eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \biggr] - \frac{2Q}{\eta^3} \, , </math> |
and,
|
<math>~\frac{1}{3c_0}\cdot \frac{d^2x_P}{d\eta^2}</math> |
<math>~=</math> |
<math>~ \frac{1}{\eta^2} \frac{d^2Q}{d\eta^2} - \frac{2}{\eta^3} \frac{dQ}{d\eta} + \frac{6Q}{\eta^4} - \frac{2}{\eta^3} \frac{dQ}{d\eta} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\eta^2} \biggl[2 -2\eta \cot(\eta - b_0) + 2\cot^2(\eta - b_0) -2\eta \cot^3(\eta - b_0) \biggr] - \frac{4}{\eta^3} \biggl[ \eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \biggr] + \frac{6Q}{\eta^4} \, . </math> |
So the relevant LAWE becomes,
|
<math>~\biggl( \frac{\eta^4}{3c_0} \biggr) \cdot</math> LAWE |
<math>~=</math> |
<math>~ \eta^2 \biggl[2 -2\eta \cot(\eta - b_0) + 2\cot^2(\eta - b_0) -2\eta \cot^3(\eta - b_0) \biggr] - 4\eta \biggl[ \eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \biggr] + 6Q </math> |
|
|
|
<math>~ + \eta^3 \biggl[4 - 2Q\biggr]\biggl\{ \frac{1}{\eta^2}\biggl[\eta -\cot(\eta - b_0) +\eta\cot^2(\eta - b_0) \biggr] - \frac{2Q}{\eta^3} \biggr\} - 2Q^2 </math> |
|
|
<math>~=</math> |
<math>~ 2\eta^2 \biggl[1 - \eta \cot(\eta - b_0) + \cot^2(\eta - b_0) - \eta \cot^3(\eta - b_0) \biggr] - 4 \biggl[ \eta^2 - \eta\cot(\eta - b_0) +\eta^2\cot^2(\eta - b_0) \biggr] + 6Q </math> |
|
|
|
<math>~ + 4\biggl[\eta^2 - \eta\cot(\eta - b_0) + \eta^2\cot^2(\eta - b_0) - 2Q \biggr] - 2Q \biggl[\eta^2 - \eta\cot(\eta - b_0) + \eta^2\cot^2(\eta - b_0) - 2Q \biggr] - 2Q^2 </math> |
|
|
<math>~=</math> |
<math>~ 2\eta^2 \biggl[Q + \cot^2(\eta - b_0) - \eta \cot^3(\eta - b_0) \biggr] - 2Q - 2Q \biggl[\eta^2 - \eta\cot(\eta - b_0) + \eta^2\cot^2(\eta - b_0) - 2Q \biggr] - 2Q^2 </math> |
|
<math>~\Rightarrow~~~\biggl( \frac{\eta^4}{6c_0} \biggr) \cdot</math> LAWE |
<math>~=</math> |
<math>~ \biggl[\eta^2 \cot^2(\eta - b_0) - \eta^3 \cot^3(\eta - b_0) \biggr] + \biggl[ 1-\eta\cot(\eta - b_0)\biggr] \biggl[\eta\cot(\eta - b_0) - \eta^2\cot^2(\eta - b_0) \biggr] - Q(1-Q) </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\eta\cot(\eta - b_0) - \eta^2\cot^2(\eta - b_0) \biggr] - Q(1-Q) </math> |
|
|
<math>~=</math> |
<math>~ 0\, . </math> |
Attempt 5
New Strategy
In the vast majority of our prior attempts to derive an analytic expression for the envelope's eigenvector, we have started with the presumption — as voiced by Beech (1988) and repeated in our accompanying derivation of the structure of the <math>~(n_c, n_e) = (5, 1)</math> bipolytrope's structure — that the most general solution to the n = 1 Lane-Emden equation can be written in the form,
|
<math>~\phi</math> |
<math>~=</math> |
<math>~A \biggl[ \frac{\sin(\eta - B)}{\eta} \biggr] \, .</math> |
But, as we have emphasized in a separate context, another expression that satisfies the relevant Lane-Emden equation has the form,
|
<math>~\phi</math> |
<math>~=</math> |
<math>~- A \biggl[ \frac{\cos(\eta - B)}{\eta} \biggr] \, .</math> |
|
We fully appreciate that for appropriately chosen and different values of the parameter, <math>~B</math>, these two functions can be made equal to one another. But, for now, let's work through our analysis pretending that they are different functions. |
This alternate "cosine" expression was not the solution of choice when we were seeking a mathematical description of the structure of an isolated, n = 1 polytrope because it does not satisfy the relevant central boundary conditions. However, it occurs to us that this alternate expression might work in the context we are considering now [20 April 2019], which deals with properties of the envelope of a bipolytrope. In this case,
|
<math>~Q \equiv - \frac{d\ln\phi}{d\ln\eta}</math> |
<math>~=</math> |
<math>~A \biggl[\frac{\cos(\eta-B)}{\eta^2} + \frac{\sin(\eta-B)}{\eta} \biggr]\cdot \frac{\eta^2}{A\cos(\eta-B)}</math> |
|
|
<math>~=</math> |
<math>~\biggl[\cos(\eta-B) + \eta\sin(\eta-B) \biggr]\cdot \frac{1}{\cos(\eta-B)}</math> |
|
|
<math>~=</math> |
<math>~1 + \eta\tan(\eta-B) \, ;</math> |
and, following along the lines of our earlier Attempt 4B discussion, a reasonable guess for the dimensionless displacement function is,
|
<math>~x_P</math> |
<math>~=</math> |
<math>~\frac{3c_1 Q}{\eta^2}</math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1 }{\eta^2}\biggl[1 + \eta\tan(\eta-B)\biggr] \, .</math> |
What are the first and second derivatives of this trial eigenfunction?
|
<math>~\frac{dx_P}{d\eta}</math> |
<math>~=</math> |
<math>~ \frac{3c_1}{\eta^2}\biggl[\tan(\eta - B) + \frac{\eta}{\cos^2(\eta-B)}\biggr] - \frac{6c_1}{\eta^3} \biggl[1 + \eta\tan(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{3c_1}{\eta^3} \biggl[\frac{\eta^2}{\cos^2(\eta-B)} -2 - \eta\tan(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{3c_1}{\eta^3\cos^2(\eta-B)} \biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr]\, . </math> |
|
<math>~\Rightarrow ~~~ \frac{d^2x_P}{d\eta^2}</math> |
<math>~=</math> |
<math>~ \biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] 3c_1 \frac{d}{d\eta}\biggl[\eta^{-3}\cos^{-2}(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \frac{3c_1}{\eta^3\cos^2(\eta-B)}\cdot \frac{d}{d\eta}\biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] 3c_1 \biggl[2\eta^{-3}\sin(\eta-B)\cos^{-3}(\eta-B) -3\eta^{-4}\cos^{-2}(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \frac{3c_1}{\eta^3\cos^2(\eta-B)} \biggl[2\eta + 4\sin(\eta-B)\cos(\eta-B) - \sin(\eta-B)\cos(\eta-B)- \eta \cos^2(\eta-B)+ \eta\sin^2(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] \cdot \biggl[2\eta\sin(\eta-B) -3\cos(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl[2\eta^2\cos(\eta-B) + 4\eta \sin(\eta-B)\cos^2(\eta-B) - \eta \sin(\eta-B)\cos^2(\eta-B)- \eta^2 \cos^3(\eta-B)+ \eta^2\sin^2(\eta-B)\cos(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl\{ 2\eta^3 \sin(\eta-B) - 4\eta\sin(\eta-B)\cos^2(\eta-B) - 2\eta^2 \sin^2(\eta-B)\cos(\eta-B) </math> |
|
|
<math>~ -3\eta^2 \cos(\eta-B) + 6\cos^3(\eta-B) +3 \eta\sin(\eta-B)\cos^2(\eta-B) </math> |
|
|
|
|
<math>~ + \eta \biggl[ 4\sin(\eta-B)\cos^2(\eta-B) - \sin(\eta-B)\cos^2(\eta-B)\biggr] + \eta^2 \biggl[ 2\cos(\eta-B) - \cos^3(\eta-B)+ \sin^2(\eta-B)\cos(\eta-B)\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl\{6\cos^3(\eta-B) + \eta^3 \biggl[2\sin(\eta-B)\biggr] </math> |
|
|
|
<math>~ + \eta \biggl[ 4\sin(\eta-B)\cos^2(\eta-B) - \sin(\eta-B)\cos^2(\eta-B) - 4\sin(\eta-B)\cos^2(\eta-B) +3 \sin(\eta-B)\cos^2(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \eta^2 \biggl[ 2\cos(\eta-B) - \cos^3(\eta-B)+ \sin^2(\eta-B)\cos(\eta-B) - 2 \sin^2(\eta-B)\cos(\eta-B) -3 \cos(\eta-B) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl[ 6\cos^3(\eta-B) + 2\eta \sin(\eta-B)\cos^2(\eta-B) - 2 \eta^2 \cos(\eta-B) + 2\eta^3 \sin(\eta-B) \biggr] \, . </math> |
Illustration
|
Above & Below: The solid, light-blue circular markers trace how the function, <math>~x_P(\eta)</math>, varies over the "radial" range, <math>~- \pi \le \eta \le \pi</math>, when <math>~c_1 = 1</math>, for various values of the parameter, <math>~B</math>; in the above panel as well as in each frame of the animation, the chosen value of <math>~B</math> is recorded in the upper-right corner of the image. (These values are also recorded in the table immediately below the animation.) The red vertical dashed line segment identifies the value of <math>~\eta</math> at which the argument of the tangent function goes to <math>~\tfrac{\pi}{2}</math> and, hence, where the function <math>~x_P(\eta)</math> flips discontinuously from plus- to minus-infinity. As explained further, below, the solid purple curve shows how the xP-intercept function varies with <math>~\eta</math>; as defined, this curve is independent of the parameter, <math>~B</math>, so it is unchanging in the animation sequence. The single larger yellow-circular marker (with a black border) shows where this "intercept" curve intersects the <math>~x_P</math> function and, therefore, where along this trial eigenfunction <math>~d\ln x_P/d\ln\eta = -1</math>; the coordinates (abscissa & ordinate) of this yellow marker are recorded in the accompanying table, for each illustrative value of <math>~B</math>. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
What is the expression for the logarithmic derivative of this eigenfunction guess?
|
<math>~\frac{d\ln x_P}{d\ln\eta} = \frac{\eta}{x_P} \cdot \frac{dx_P}{d\eta}</math> |
<math>~=</math> |
<math>~ \frac{\eta^3}{3c_1} \biggl[1 + \eta\tan(\eta-B)\biggr]^{-1} \biggl\{ \frac{3c_1}{\eta^2}\biggl[\tan(\eta - B) + \frac{\eta}{\cos^2(\eta-B)}\biggr] - \frac{6c_1}{\eta^3} \biggl[1 + \eta\tan(\eta-B)\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{\cos (\eta-B)}{\cos(\eta-B) + \eta\sin(\eta-B)}\biggr] \biggl\{ \frac{\eta}{\cos^2(\eta-B)} \biggl[\sin(\eta - B)\cos(\eta-B) +\eta\biggr] - \frac{2}{\cos^2(\eta-B)} \biggl[\cos^2(\eta-B) + \eta\sin(\eta-B)\cos(\eta-B)\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\eta^2 - \eta\sin(\eta - B)\cos(\eta-B) - 2\cos^2(\eta-B)}{\cos^2(\eta-B) + \eta\sin(\eta-B) \cos(\eta-B)} \, . </math> |
At the surface of the bipolytropic configuration — that is, presumably when <math>~\eta = \eta_s</math> — we must find that this logarithmic derivative is negative one. So, for a given value of the parameter, <math>~B</math>, what is the value of <math>~\eta_s</math>? Well …
|
<math>~\frac{d\ln x_P}{d\ln\eta}</math> |
<math>~=</math> |
<math>~-1</math> |
|
<math>~\Rightarrow ~~~ -\cos^2(\eta-B) - \eta\sin(\eta-B) \cos(\eta-B)</math> |
<math>~=</math> |
<math>~\eta^2 - \eta\sin(\eta - B)\cos(\eta-B) - 2\cos^2(\eta-B)</math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~\eta^2 - \cos^2(\eta-B)</math> |
|
<math>~\Rightarrow ~~~ \eta</math> |
<math>~=</math> |
<math>~\pm \cos(\eta-B)\, .</math> |
Now, given that,
|
<math>~\tan(\eta-B) </math> |
<math>~=</math> |
<math>~\pm \biggl[ \frac{\sqrt{1-\cos^2(\eta-B)}}{\cos(\eta-B)} \biggr] \, ,</math> |
we see that,
|
<math>~x_P\biggr|_\mathrm{intercept}</math> |
<math>~=</math> |
<math>~\frac{3c_1 }{\eta^2}\biggl\{ 1 \pm \eta \biggl[ \frac{\sqrt{1-\cos^2(\eta-B)}}{\cos(\eta-B)} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1 }{\eta^2}\biggl\{ 1 \pm \eta \biggl[ \frac{\sqrt{1-\cos^2(\eta-B)}}{\cos(\eta-B)} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1 }{\eta^2}\biggl\{ 1 \pm \eta \biggl[ \frac{\sqrt{1-\eta^2}}{\eta} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{3c_1 }{\eta^2}\biggl\{ 1 \pm \sqrt{1-\eta^2}\biggr\} \, .</math> |
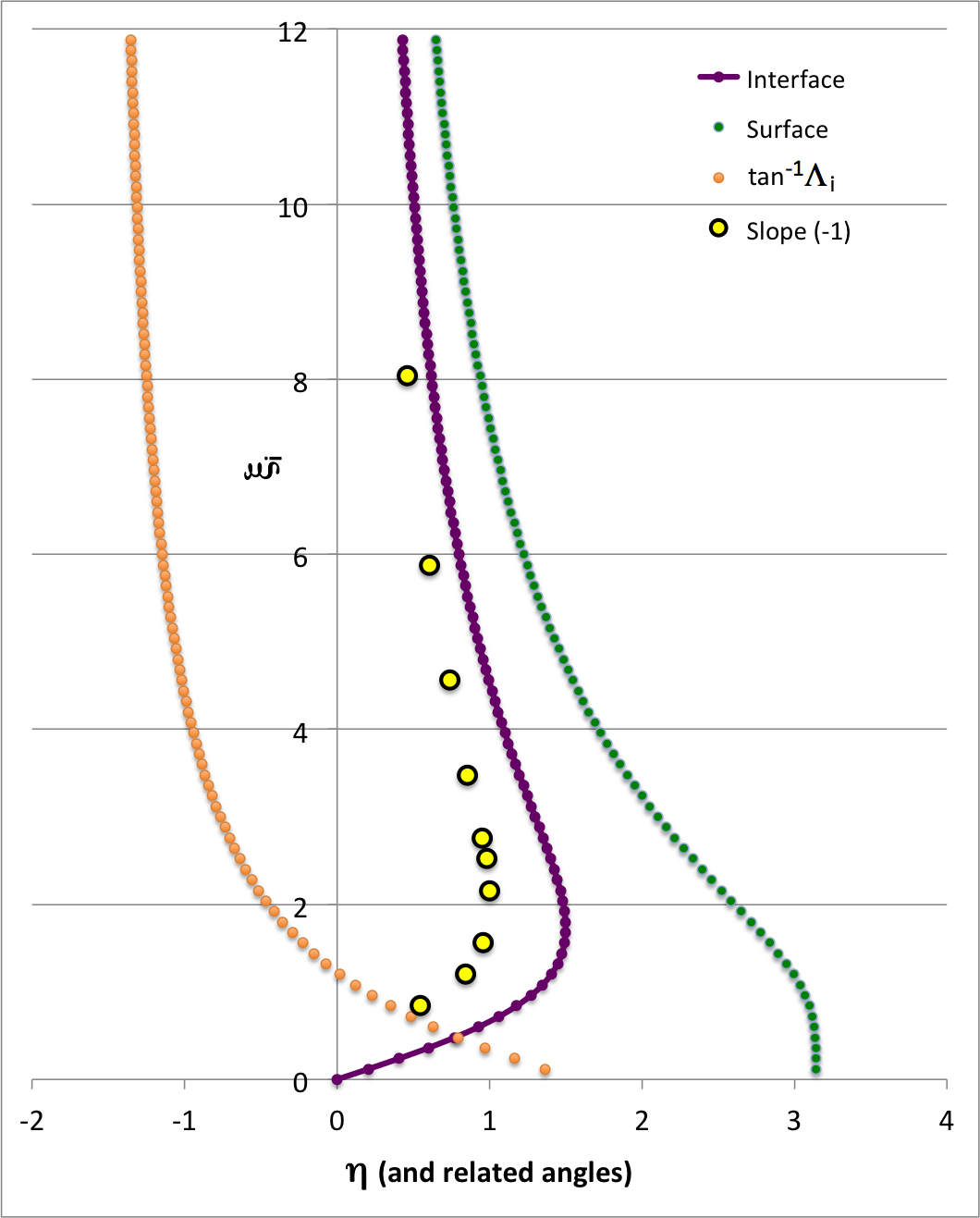
The solid-purple, xP-intercept curve that appears in the above figure/animation is defined by this function. Notice that this function never exceeds unity. This presumably means that if the tangent-based <math>~x_P</math> eigenfunction is the correct solution to the envelope's LAWE, then the dimensionless radius, <math>~\eta_s</math>, of the bipolytrope must never exceed unity.
The following diagram — the original of which appears in our accompanying discussion of the equilibrium properties of bipolytropic configurations having <math>~(n_c, n_e) = (5, 1)</math> — shows how <math>~\eta_i</math> (purple curve) and <math>~\eta_s</math> (green curve) vary with the interface location <math>~\xi_i</math> (ordinate). The solid yellow circular markers (with black edges) identify where the logarithmic derivative of the dimensionless displacement function, <math>~d\ln x_P/d\ln\eta</math>, equals negative one. If <math>~x_P</math> is the correct eigenfunction for the marginally unstable bipolytropic configuration, one of these yellow circular markers should coincide with the green curve, that is, it should be associated with the configuration's surface. Since the curve identified by the yellow circular markers does not appear to intersect the green curve, we conclude that we have not yet identified the correct eigenfunction.
Is This Compatible With LAWE
In an effort to track the two <math>~Q(\eta)</math> functions separately, we will add a subscript zero to the one that applies to the structural properties of the underlying equilibrium configuration. Again, we will be focused on finding a solution in the case where <math>~\sigma_c^2 = 0</math> and <math>~n = 1</math>, that is — see also our above discussion — the relevant envelope LAWE is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x_P}{d\eta^2} + \biggl[ 2 - Q_0 \biggr] \frac{2}{\eta}\cdot \frac{dx_P}{d\eta} -2\alpha_g Q_0 \cdot \frac{x_P}{\eta^2} \, , </math> |
where, drawing from our discussion of the n = 1 envelope's equilibrium structure,
|
<math>~Q_0</math> |
<math>~=</math> |
<math>~\biggl[ - \frac{d\ln\phi}{d\ln\eta} \biggr]_\mathrm{n=1} = - \frac{\eta}{\phi}\biggl[ \frac{d\phi}{d\eta} \biggr]_\mathrm{n=1}</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{1}{\sin(\eta - B_0)} \biggr]\biggl[ \eta\cos(\eta-B_0) - \sin(\eta-B_0) \biggr]</math> |
<math>~=</math> |
<math>~\biggl[1 - \eta\cot(\eta-B_0) \biggr] \, .</math> |
Hence, after recognizing that for this specific case, <math>~\alpha_g = +1</math>, we have,
|
LAWE |
<math>~=</math> |
<math>~ \frac{d^2x_P}{d\eta^2} + \biggl[ 2 - Q_0 \biggr] \frac{2}{\eta}\cdot \frac{dx_P}{d\eta} -2 Q_0 \cdot \frac{x_P}{\eta^2} </math> |
|
<math>~\Rightarrow ~~~</math> LAWE |
<math>~=</math> |
<math>~ \frac{3c_1}{\eta^4\cos^3(\eta-B)} \biggl[ 6\cos^3(\eta-B) + 2\eta \sin(\eta-B)\cos^2(\eta-B) - 2 \eta^2 \cos(\eta-B) + 2\eta^3 \sin(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \biggl[ 2 - Q_0 \biggr] \frac{2}{\eta}\cdot \frac{3c_1}{\eta^3\cos^2(\eta-B)} \biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] - \frac{2 Q_0}{\eta^2} \cdot \frac{3c_1 }{\eta^2}\biggl[1 + \eta\tan(\eta-B)\biggr] </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{\eta^4\cos^3(\eta-B)}{6c_1} \biggr] \cdot</math> LAWE |
<math>~=</math> |
<math>~ \biggl[ 3\cos^3(\eta-B) + \eta \sin(\eta-B)\cos^2(\eta-B) - \eta^2 \cos(\eta-B) + \eta^3 \sin(\eta-B) \biggr] </math> |
|
|
|
<math>~ + \biggl[ 2 - Q_0 \biggr]\cos(\eta - B)\biggl[\eta^2 -2\cos^2(\eta-B) - \eta\sin(\eta-B)\cos(\eta-B)\biggr] - Q_0 \cos^3(\eta - B) \biggl[1 + \eta\tan(\eta-B)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ 3\cos^3(\eta-B) + \eta \sin(\eta-B)\cos^2(\eta-B) - \eta^2 \cos(\eta-B) + \eta^3 \sin(\eta-B) </math> |
|
|
|
<math>~ -4\cos^3(\eta-B) - 2\eta\sin(\eta-B)\cos^2(\eta-B) + 2\eta^2\cos(\eta - B) </math> |
|
|
|
<math>~ - Q_0\biggl\{ \biggl[\eta^2\cos(\eta - B) -2\cos^3(\eta-B) - \eta\sin(\eta-B)\cos^2(\eta-B)\biggr] + \biggl[\cos^3(\eta - B) + \eta\sin(\eta-B)\cos^2(\eta - B)\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\cos^3(\eta-B) - \eta \sin(\eta-B)\cos^2(\eta-B) + \eta^2 \cos(\eta-B) + \eta^3 \sin(\eta-B) + Q_0\biggl[ \cos^3(\eta-B) - \eta^2\cos(\eta - B) \biggr] </math> |
|
Quick Check: Now, if we set <math>~Q_0 = 1 + \eta\tan(\eta-B)</math>, these RHS terms should sum to zero. Let's check.
Excellent! |
Now, let's plug in the expression for the structural <math>~Q_0</math>. Specifically, we want,
|
<math>~Q_0</math> |
<math>~\equiv</math> |
<math>~\biggl[ 1 - \eta\cot(\eta-B_0) \biggr]</math> |
|
|
<math>~\equiv</math> |
<math>~\biggl[ 1 + \eta\tan(\eta-B_0 - \tfrac{\pi}{2} \pm m\pi) \biggr] \, ,</math> |
in which case we have,
|
<math>~\biggl[ \frac{\eta^4\cos^3(\eta-B)}{6c_1} \biggr] \cdot</math> LAWE |
<math>~\rightarrow</math> |
<math>~ -\cos^3(\eta-B) - \eta \sin(\eta-B)\cos^2(\eta-B) + \eta^2 \cos(\eta-B) + \eta^3 \sin(\eta-B) </math> |
|
|
|
<math>~ + \biggl[ 1 + \eta\tan(\eta-B_0 - \tfrac{\pi}{2} \pm m\pi) \biggr] \cdot \biggl[ \cos^3(\eta-B) - \eta^2\cos(\eta-B) \biggr] \, . </math> |
As we have just shown, above, in the context of a "Quick Check", the expression on the RHS will go to zero if we adopt the transformation, <math>~[B_0 + \tfrac{\pi}{2} \mp m\pi] \rightarrow B</math>. Does this help shift the coordinate, <math>~\eta</math>?
See Also
- K. De et al. (12 October 2018, Science, Vol. 362, No. 6411, pp. 201 - 206), A Hot and Fast Ultra-stripped Supernova that likely formed a Compact Neutron Star Binary.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |